附录⚓︎

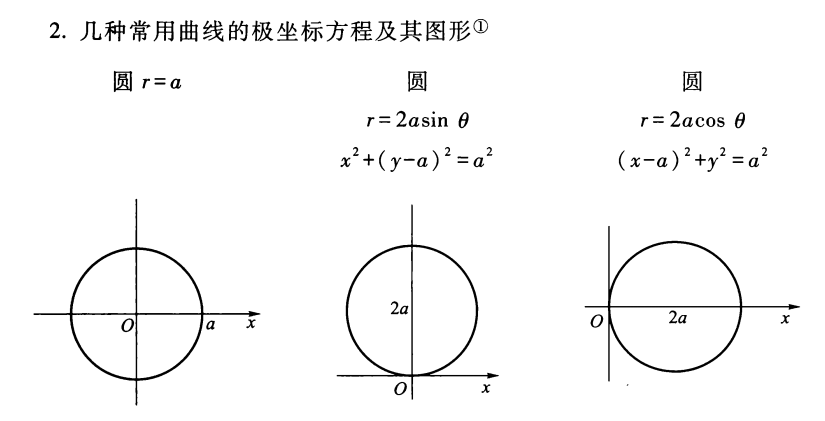
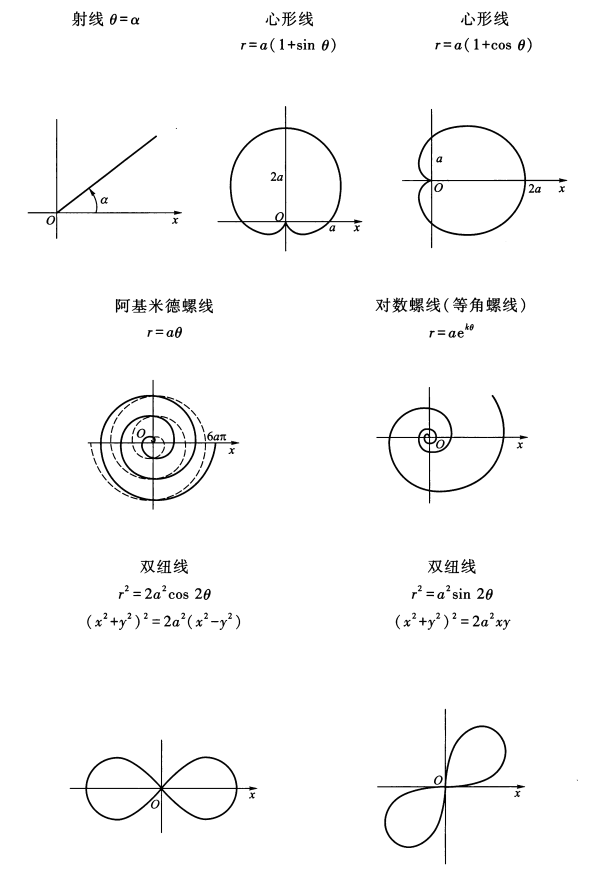
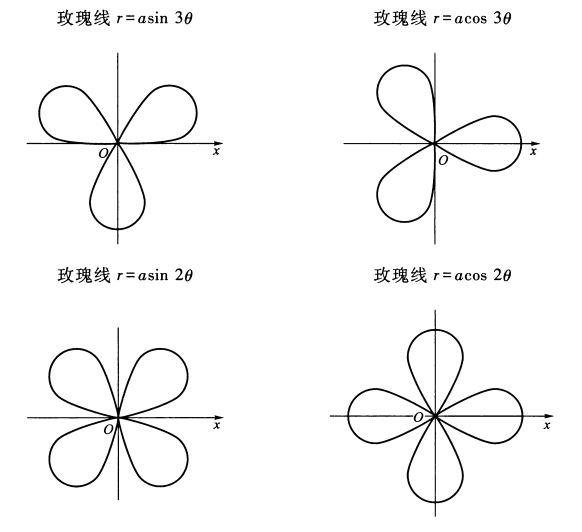
常用曲线极坐标方程及其图形⚓︎

积化和差	和差化积
\(\sin\alpha\cos\beta = \dfrac{\sin(\alpha + \beta) + \sin(\alpha - \beta)}{2}\)	\(\sin\alpha + \sin\beta = 2\sin\dfrac{\alpha + \beta}{2}\cos\dfrac{\alpha - \beta}{2}\)
\(\cos\alpha\sin\beta = \dfrac{\sin(\alpha + \beta) - \sin(\alpha - \beta)}{2}\)	\(\sin\alpha - \sin\beta = 2\cos\dfrac{\alpha + \beta}{2}\sin\dfrac{\alpha - \beta}{2}\)
\(\cos\alpha\cos\beta = \dfrac{\cos(\alpha + \beta) + \cos(\alpha - \beta)}{2}\)	\(\cos\alpha + \cos\beta = 2\cos\dfrac{\alpha + \beta}{2}\cos\dfrac{\alpha - \beta}{2}\)
\(\sin\alpha\sin\beta = -\dfrac{\cos(\alpha + \beta) - \cos(\alpha - \beta)}{2}\)	\(\cos\alpha - \cos\beta = -2\sin\dfrac{\alpha + \beta}{2}\sin\dfrac{\alpha - \beta}{2}\)

正弦	余弦
\(\sin^2\theta = \dfrac{1 - \cos2\theta}{2}\)	\(\cos^2\theta = \dfrac{1 + \cos2\theta}{2}\)
\(\sin^3\theta = \dfrac{3\sin\theta - \sin3\theta}{4}\)	\(\cos^3\theta = \dfrac{3\cos\theta + \cos3\theta}{4}\)

评论区

如果大家有什么问题或想法，欢迎在下方留言~