第九章 多元函数积分学⚓︎
约 5528 个字 预计阅读时间 28 分钟
注
对于表述复杂的积分区域 ( 比如用两个曲面表示直线的一般式方程 ),可以先对方程进行化简 ( 如果可以的话 ),然后再计算积分
二重积分⚓︎
概念⚓︎
引入
求下列实际问题,我们采用与推导定积分时类似的步骤:
- 分割
- 近似
- 作和
- 取极限
定义:
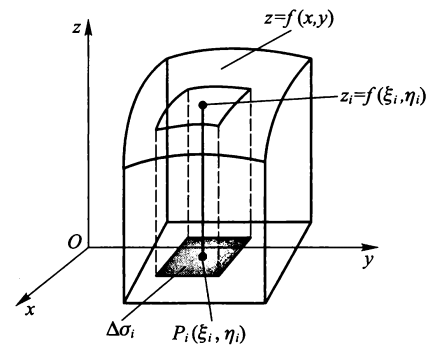
设二元函数 \(f(P) = f(x, y)\) 在平面有界闭区域 \(\sigma\) 上有界,用曲线网将区域 \(\sigma\) 任意分成 n 个 ( 彼此无公共内点的 ) 小闭区域 \(\Delta \sigma_1, \Delta \sigma_2, \dots, \Delta \sigma_n\),仍以 \(\Delta \sigma_i\) 记为小区域的面积,
- \(\forall P_i(\xi_i, \eta_i) \in \Delta \sigma_i, f(\xi_i, \eta_i) \Delta \sigma_i\) 被称为积分元
- 积分和式:\(\sum\limits_{i = 1}^n f(\xi_i, \eta_i) \Delta \sigma_i\)
-
二重积分 ( 黎曼积分 ):\(\iint\limits_\sigma f(x, y)\mathrm{d}\sigma = \lim\limits_{\lambda \rightarrow 0} \sum\limits_{i = 1}^n f(\xi_i, \eta_i) \Delta \sigma_i\),其中
- 被积函数:\(f(P) = f(x, y)\)
- 积分区域:\(\sigma\)
- 被积表达式:\(f(x, y)\mathrm{d}\sigma\)
- 积分变量:x, y
- 面积元素:\(\mathrm{d}\sigma\)
定理 1:若 f(x, y) 在有界闭区域 \(\sigma\) 上连续,则 f(x, y) 在 \(\sigma\) 上可积。
补充
- 平面图形的面积 $\sigma = \iint\limits_\sigma \mathrm{d}\sigma $
- 几何意义:曲顶柱体的体积
性质⚓︎
- \(\iint\limits_\sigma [f(x, y) \pm g(x, y)] \mathrm{d}\sigma = \iint\limits_\sigma f(x, y) \mathrm{d}\sigma \pm \iint\limits_\sigma g(x, y) \mathrm{d}\sigma\)
- \(\iint\limits_\sigma kf(x, y) \mathrm{d}\sigma = k\iint\limits_\sigma f(x, y) \mathrm{d}\sigma\) (k 为任意常数 )
- \(\iint\limits_\sigma 1 \mathrm{d}\sigma = \iint\limits_\sigma \mathrm{d}\sigma = \sigma\)
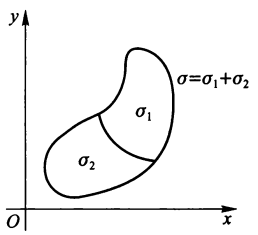
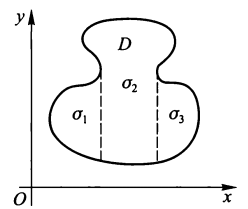
- 若 \(\sigma\) 可分解为 2 个不共内点的区域 \(\sigma_1, \sigma_2\),记作 \(\sigma = \sigma_1 + \sigma_2\),则有:
-
- 若 \(\iint\limits_\sigma f(x, y) \mathrm{d}\sigma\) 存在,\(f(x, y) \ge 0\),则 \(\iint\limits_\sigma f(x, y) \mathrm{d}\sigma \ge 0\)
- 若 \(f(x, y) \le g(x, y), (x, y) \in \sigma\),则 \(\iint\limits_\sigma f(x, y) \mathrm{d}\sigma \le \iint\limits_\sigma g(x, y)\mathrm{d} \sigma\)
-
- 若 \(f(x, y) \ge 0, f(x, y) \not\equiv 0, (x, y) \in \sigma\) 且 \(f(x, y)\) 连续,则 \(\iint\limits_\sigma f(x, y) \mathrm{d}\sigma > 0\)
- 若 \(f(x, y) \le g(x, y), f(x, y) \not\equiv g(x, y), (x, y) \in \sigma\) 且 \(f(x, y), g(x, y)\) 连续,则 \(\iint\limits_\sigma f(x, y) \mathrm{d}\sigma < \iint\limits_\sigma g(x, y) \mathrm{d}\sigma\)
-
\(|\iint\limits_\sigma f(x, y) \mathrm{d}\sigma| \le \iint\limits_\sigma |f(x, y)| \mathrm{d}\sigma\)
-
二重积分中值定理:若 f(x, y) 在有界闭区域 \(\sigma\) 上连续,则在 \(\sigma\) 上至少存在一点 \(P(x^*, y^*)\),使得 \(\iint\limits_\sigma f(x, y) \mathrm{d}\sigma = f(x^*, y^*) \sigma\)
- 推论:\(m \sigma \le \iint\limits_\sigma f(x, y) \mathrm{d}\sigma \le M \sigma\)
- 几何意义:曲顶柱体的体积 = 以 \(\sigma\) 为底,\(f(x^*, y^*)\) 为高的柱体体积
计算⚓︎
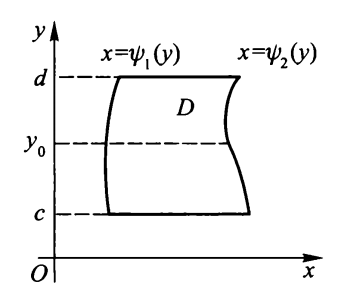
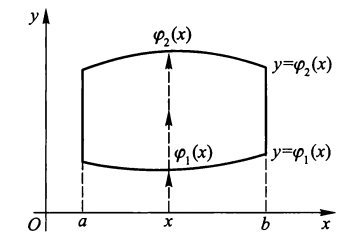
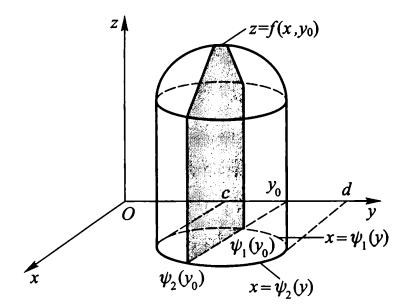
直角坐标系⚓︎
x- 型区域 & y- 型区域
注:考试中往往用 \(\partial D\) 表示积分区域 \(D\) 的边界

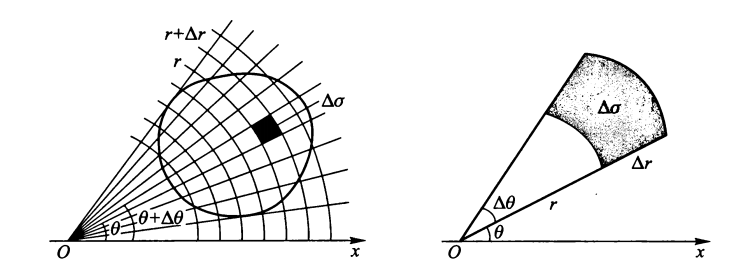
极坐标系⚓︎
直角坐标 \(\Rightarrow\) 极坐标

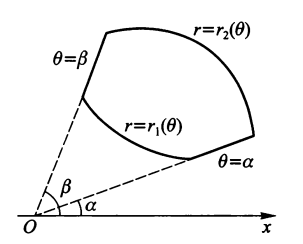
\(\sigma: r_1(\theta) \le r \le r_2(\theta), \alpha \le \theta \le \beta\),即 \(\sigma\) 是由曲线 \(r = r_1(\theta)\)( 下曲线 ),\(r = r_2(\theta)\)( 上曲线 ),及射线 \(\theta = \alpha, \theta = \beta\) 所围成的区域,则:
\(\sigma: r_1(\theta) \le r \le r_2(\theta), \alpha \le \theta \le \beta\)
\(\sigma: 0 \le r \le r(\theta), \alpha \le \theta \le \beta\)
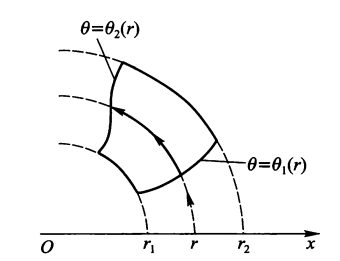
\(\sigma: \theta_1(r) \le \theta \le \theta_2(r), r_1 \le r \le r_2\),即 \(\sigma\) 是由曲线 \(\theta = \theta_1(r), \theta = \theta_2(r)\) 与圆 \(r = r_1, r = r_2\) 所围成的区域,则有:
\(\sigma: r = R\)
\(\sigma: 0 \le r \le 2R \cos \theta, -\dfrac{\pi}{2} \le \theta \le \dfrac{\pi}{2}\)
总结
- 我们应根据区域的特征,选取更容易计算的方法求解。
- 要熟悉一些特殊图形的曲线,比如摆线、心形线等 ( 见《微积分》( 上 ) 教材的附录部分 )
-
小技巧:改良版极坐标法 ( 有些题目无法直接用极坐标做,则采用此法 )
- 设 \(x = ar \cos^n \theta, y = br \sin^n \theta\),记 \(|J| = nabr \cos^{n-1} \theta \sin^{n-1} \theta\)
- $ \iint\limits_\sigma f(x, y) \mathrm{d}\sigma = \int_\alpha^\beta \mathrm{d}\theta \int_{r_1(\theta)}^{r_2(\theta)}f(ar \cos^n \theta, br \sin^n \theta)|J| \mathrm{d}r$
三重积分⚓︎
概念⚓︎
引入
-
设 V 为一空间立体,\(P_0(x_0, y_0, z_0) \in V\),取包含 \(P_0\) 的 \(\Delta V\),质量为 \(\Delta m\),若 \(\lim\limits_{\Delta V \rightarrow P_0} \dfrac{\Delta m}{\Delta V}\) 存在,则该极限值被称为在 \(P_0\) 处的体密度。
-
质量 \(M = \lim\limits_{\lambda \rightarrow 0}\sum\limits_{i = 1}^nf(\xi_i, \eta_i, \zeta_i)\Delta V_i\)
定义:
设 f(x, y, z) 是空间有界闭区域 V 的有界函数,将 V 任意分成 n 个小闭区域 \(\Delta V_1, \Delta V_2, \dots, \Delta V_n\),其中 \(\Delta V_i\) 既表示第 i 个小闭区域,也表示其体积。在每个 \(\Delta V_i\) 上任取一点 \((\xi_i, \eta_i, \zeta_i)\),作乘积再求和得上述质量等式的右侧。若 \(\lambda\) 为各小闭区域直径最大值,当 \(\lambda \rightarrow 0\) 时,该和式极限总存在,称此极限为 f(x, y, z) 在 V 的三重积分,记作 \(\iiint\limits_{V} f(x, y, z) \mathrm{d}V\),其中 \(\mathrm{d}V\) 叫做体积元素
在直角坐标系中,三重积分也可记作 \(\iiint\limits_{V} f(x, y, z) \mathrm{d}x\mathrm{d}y\mathrm{d}z\)
直角坐标系的计算⚓︎
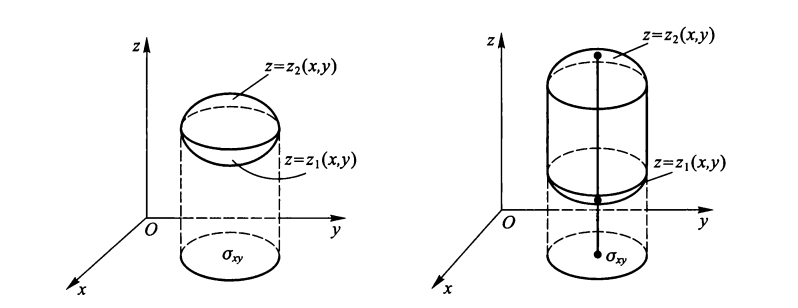
投影法
若立体 V 的投影区域为:
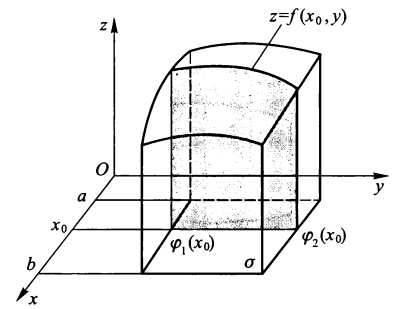
\(V = \{(x, y, z): z_1(x, y) \le z \le z_2(x, y), (x, y) \in \sigma_{xy}\}\)
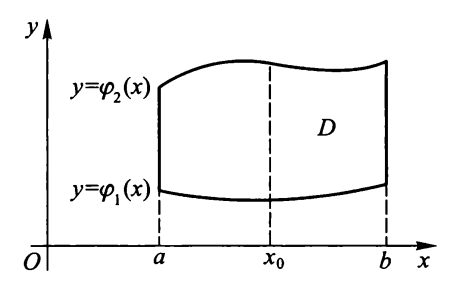
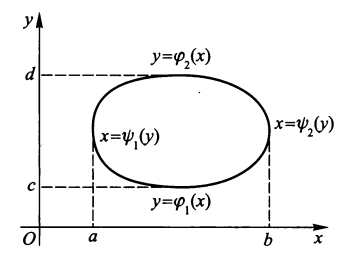
\(\varphi_1(x) \le y \le \varphi_2(x), a \le x \le b\)
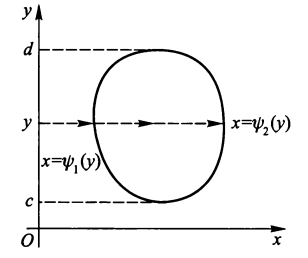
\(\psi_1(y) \le x \le \psi_2(y), c \le y \le d\)
\(V = \{(x, y, z): y_1(x, z) \le y \le y_2(x, z), (x, z) \in \sigma_{zx}\}\)
若 \(\sigma_{zx}\) 为 x- 型区域:\(z_1(x) \le z \le z_2(x), a \le x \le b\),则:
\(V = \{(x, y, z): x_1(y, z) \le x \le x_2(y, z), (y, z) \in \sigma_{yz}\}\)
注:对有些较难画的曲面,关键是要画出曲面与曲面的交线,交线与交线的交点,并确定投影区域及上曲面、下曲面方程
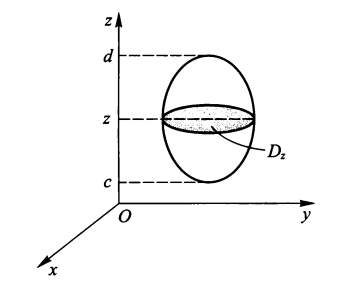
平面截割法
\(V = \{(x, y, z): (x, y) \in D_z, c \le z \le d\}\)
若 \(D_z\) 为 x- 型区域,则: $$ \iiint\limits_V f(x, y, z) \mathrm{d}V = \int_c^d \mathrm{d}z \int_{x_1(z)}^{x_2(z)} \mathrm{d}x \int_{y_1(x, z)}^{y_2(x, z)} f(x, y, z) \mathrm{d}y $$
\(V = \{(x, y, z): (x, z) \in D_y, c \le y \le d\}\)
\(V = \{(x, y, z): (y, z) \in D_x, a \le x \le b\}\)
有时 ( 比如用极坐标表示截面更加方便时 ),平面截割法 + 极坐标转换的食用效果更佳
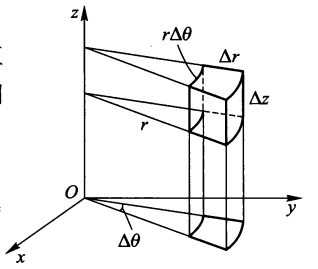
柱面坐标系的计算⚓︎
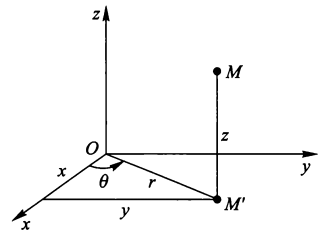
柱面坐标系:
柱面坐标系的坐标曲面:
- 一族以 Oz 轴为对称轴的圆柱面:\(r = r_i\)( 常 ),即 \(x^2 + y^2 = r_i^2\)
- 一族通过 Oz 轴的半平面:\(\theta = \theta_i\)( 常 ),即 \(y = x\tan \theta_i\)
- 一族垂直 Oz 轴的平面 \(z = z_i\)( 常 )
( 推导过程略 )
注:柱面坐标系本质上是投影法 + 极坐标转换
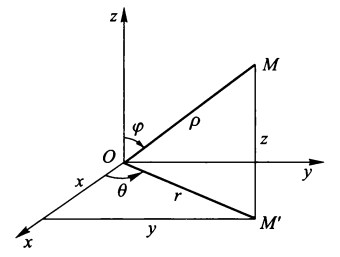
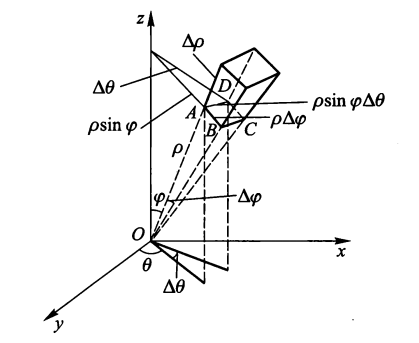
球面坐标系的计算⚓︎
球面坐标系:
其中 \(\varphi\) 为 \(\overrightarrow{OM}\) 为与 Oz 轴的夹角,\(\theta\) 为投影点 M' 的极角,\(\rho\) 为点 M 到原点的距离
球面坐标系的坐标曲面:
- 一族中心在原点的球面:\(\rho = r_i\)( 常 ),即 \(x^2 + y^2 + z^2= r_i^2\)
- 一族顶点在原点而对称轴与 Oz 轴重合的圆锥面:\(\varphi = \varphi_i\)( 常 ),即 \(x^2 + y^2 - z^2 \tan^2\varphi_i = 0\)
- 一族通过 Oz 轴的半平面 \(\theta = \theta_i\)( 常 ),即 \(y = x\tan \theta_i\)
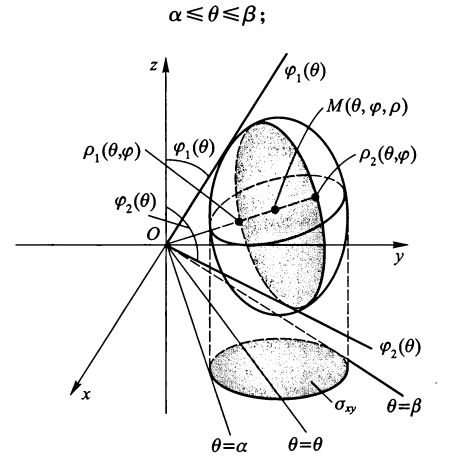
直角坐标 \(\Rightarrow\) 球面坐标
从而:
其中:\(\rho_1(\theta, \varphi) \le \rho \le \rho_2(\theta, \varphi),\ \varphi_1(\theta) \le \varphi \le \varphi_2(\theta),\ \alpha \le \theta \le \beta\)
“椭球”坐标系
设坐标为:
令 \(|J| = abc\rho^2 \sin \varphi\),则
总结
- 根据区域的特征选取最容易计算的方法
- 需要熟记常用的二次曲面方程,否则很难确定积分区域的范围
该选取哪个坐标系呢?
按照笔记给出的顺序 ( 直角坐标系的投影法、平面截割法,柱面坐标系、球面坐标系 ),根据情况,看哪个简单就用那个。
有时看似无法用直角坐标系做,但如果我们稍微变换一下积分区域,比如从 x- 型区域转化为 y- 型区域,就能够成功计算积分了。
不要一上来就用球面坐标系,有时候可能用直角坐标系更快一些。
第一类曲线积分与第一类曲面积分⚓︎
第一类曲线积分⚓︎
定义:设函数 f(P) 是定义在以 A, B 为端点的光滑曲线 \(\Gamma\) 上的有界函数,在 \(\Gamma\) 上任意取点:\(A = M_0, M_1, M_2, \dots, M_n = B\),将曲线分成 n 个部分。记弧 \(\widehat{M_{i-1}M_i}\) 的长度为 \(\Delta s_i\),并在 \(\widehat{M_{i-1}M_i}\) 任取一点 \(P_i(\xi_i, \eta_i, \zeta_i)\),作和 \(\sum\limits_{i-1}^nf(P_i)\Delta s_i\)。记 \(\lambda = \max\{\Delta s_i: 1 \le i \le n\}\)。称下列极限值为 \(f(P)\) 沿 \(\Gamma\) 的第一类曲线积分 ( 若存在 ):
第一类曲线积分又被称为对弧长曲线积分
计算
本质上是将第一类曲线积分 \(\Rightarrow\) 一元函数定积分
若 \(\Gamma: \begin{cases}x = x(t) \\ y = y(t) \\ z = z(t)\end{cases}, \alpha \le t \le \beta\),则:
若 \(\Gamma: y = \varphi(x), x \in [a, b]\),则
若 \(\Gamma: x = \psi(y), y \in [c, d]\),则
若 \(\Gamma: r = r(\theta), \theta \in [\alpha, \beta]\),则
第一类曲线积分也具有二重积分的八条性质。
第一类曲面积分⚓︎
定义:设函数 f(x, y, z) 是定义在有界光滑曲面 S 上的有界函数,用曲线网将 S 分成任意 n 部分:\(\Delta S_1, \Delta S_2, \dots, \Delta S_n\),仍用 \(\Delta S_i\) 记 \(\Delta S_i\) 的面积,并在 \(\Delta S_i\) 上任取点 \(P_i(\xi_i, \eta_i, \zeta_i)\),作和 \(\sum\limits_{i-1}^nf(P_i)\Delta S_i\)。记 \(\lambda\) 为 \(\Delta S_i\) 直径最大者。称下列极限值为 \(f(P)\) 沿 S 的第一类曲面积分 ( 若存在 ):
第一类曲面积分又被称为对面积曲面积分
计算
本质上是将第一类曲面积分 \(\Rightarrow\) 二重积分
若 \(S: z = z(x, y), (x, y) \in \sigma_{xy}\)(\(\sigma_{xy}\) 是 S 在 Oxy 平面上的投影 ),则:
注:若缺少某些变量,比如 \(z = 2\sqrt{x}\),这时积分内根号里的内容还是 \(1 + z'^2_x + z'^2_y\),没有省略
若 \(S: y = y(x, z), (x, z) \in \sigma_{zx}\)(\(\sigma_{zx}\) 是 S 在 Ozx 平面上的投影 ),则:
若 \(S: x = x(y, z), (y, z) \in \sigma_{yz}\)(\(\sigma_{yz}\) 是 S 在 Oyz 平面上的投影 ),则:
注
任意曲面与柱体相交形成的交曲面,它的投影区域即为柱体的底面。这样,我们可以直接使用上面的计算方法求解。
常见应用:给定面密度 e 和曲面方程,求该金属薄板的质量
点函数积分的概念、性质及应用⚓︎
概念⚓︎
定义:设 \(\Omega \subset \mathbf{R}(or\ \mathbf{R}^2\ or\ \mathbf{R^3})\),且 \(\Omega\) 为有界闭区域。设 \(u = f(P), P \in \Omega\) 为 \(\Omega\) 上的有界点函数。任用一种分割法将 \(\Omega\) 分成 n 个子闭形体 \(\Delta \Omega_1, \Delta \Omega_2, \dots, \Delta \Omega_n\),这些子闭形体的度量仍记为 \(\Delta \Omega_i(i = 1, 2, \dots, n)\),设 \(\lambda_i = \max \{\rho(P_1, P_2): P_1, P_2 \in \Delta \Omega_i\}\) 为 \(\Delta \Omega_i\) 的直径,令 \(\lambda = \max\{\lambda_i: 1 \le i \le n\}\)。称下列极限值为点函数 \(f(P)\) 在 \(\Omega\) 上的积分 ( 若存在 ):
- 积分元:\(f(P_i)\Delta \Omega_i\)
- 积分和式:\(\sum\limits_{i = 1}^n f(P_i) \Delta \Omega_i\)
- 积分区域:\(\Omega\)
- 被积函数:\(f(P)\)
- 积分变量:\(P\)
- 被积表达式:\(f(P) \mathrm{d} \Omega\)
- 度量元素:\(\mathrm{d} \Omega\)
物理意义:当 \(f(P) \ge 0\) 时,\(\int\limits_\Omega f(P) \mathrm{d} \Omega\) 表示密度为 \(\rho = f(P)\) 的空间形体的质量 M。特别地,当 \(f(P) \equiv 1\) 时,\(\int\limits_{\Omega}\mathrm{d} \Omega = \Omega\)
定理 2:若 \(f(P)\) 在有界闭区域 \(\Omega\) 上连续,则 \(f(P)\) 在 \(\Omega\) 上可积。
性质⚓︎
设 \(f(P), g(P)\) 在有界闭区域 \(\Omega\) 上都可积,有:
-
线性运算法则:
- \(\int\limits_\Omega [f(P) \pm g(P)] \mathrm{d}\Omega = \int\limits_\Omega f(P) \mathrm{d}\sigma \pm \int\limits_\Omega g(P) \mathrm{d}\Omega\)
- \(\int\limits_\Omega kf(P) \mathrm{d}\Omega = k\int\limits_\Omega f(P) \mathrm{d}\Omega\) (k 为任意常数 )
-
\(\int\limits_\Omega f(P) \mathrm{d}\Omega = \int\limits_{\Omega_1} f(P) \mathrm{d}\Omega + \int\limits_{\Omega_2} f(P) \mathrm{d}\Omega\),其中 \(\Omega_1 \cup \Omega_2 = \Omega\),且 \(\Omega_1, \Omega_2\) 无公共内点
-
- 若 \(f(P) \ge 0, P \in \Omega\),则 \(\int\limits_\Omega f(P) \mathrm{d}\Omega \ge 0\)
- 若 \(f(P)\) 连续,\(f(P) \ge 0, f(P) \not \equiv 0, P \in \Omega\),则 \(\int\limits_\Omega f(P) \mathrm{d} \Omega > 0\)
-
- 若 \(f(P) \le g(P), P \in \Omega\),则 \(\int\limits_\Omega f(P) \mathrm{d}\Omega \le \int\limits_\Omega g(x, y) \mathrm{d}\Omega\)
- 若 \(f(P), g(P)\) 连续,\(f(P) \le g(P), f(P) \not\equiv g(P), P \in \Omega\) 且 \(f(x, y), g(x, y)\) 连续,则 \(\int\limits_\Omega f(P) \mathrm{d}\Omega < \int\limits_\Omega g(x, y) \mathrm{d}\Omega\)
-
若 \(f(P)\) 连续,\(|\int\limits_\Omega f(P) \mathrm{d}\Omega| \le \int\limits_\Omega |f(P)| \mathrm{d}\Omega\)
-
若 \(f(P)\) 在积分区域 \(\Omega\) 上满足 \(m \le f(P) \le M\),其中 \(m, M\) 均为常数,则
- 中值定理:若 f(P) 在有界闭区域 \(\Omega\) 上连续,则至少存在一点 \(P^* \in \Omega\),使得
\(f(P^*) = \dfrac{\int\limits_\Omega f(P) \mathrm{d}\Omega}{\Omega}\) 被称为函数 \(f(P)\) 在 \(\Omega\) 上的平均值
分类⚓︎
- \(\Omega = [a, b] \subset \mathbf{R}, f(P) = f(x), x \in [a, b]\) —— 一元函数定积分
- \(\Omega = s \subset \mathbf{R}^2\),s 是平面曲线,\(f(P) = f(x, y), (x, y) \in s\) —— 第一类平面曲线积分
- \(\Omega = s \subset \mathbf{R}^3\),s 是空间曲线,\(f(P) = f(x, y, z), (x, y, z) \in s\) —— 第一类空间曲线积分
- \(\Omega = \sigma \subset \mathbf{R}^2\),\(\sigma\) 是平面区域,\(f(P) = f(x, y), (x, y) \in \sigma\) —— 二重积分
- \(\Omega = S \subset \mathbf{R}^3\),S 是空间曲面,\(f(P) = f(x, y, z), (x, y, z) \in S\) —— 第一类曲面积分
- \(\Omega = V \subset \mathbf{R}^3\),V 是空间曲面,\(f(P) = f(x, y, z), (x, y, z) \in V\) —— 三重积分
对称区域上的点函数积分⚓︎
小贴士
如果发现积分函数过于复杂,难以直接计算,不妨停下笔,先观察积分函数的特征,观察是否函数是否具有对称性,若有则及时化简,这样也许会大幅降低计算难度
- 若 \(\Omega = \Omega_1 + \Omega_2\),且 \(\Omega_1, \Omega_2\) 关于 Oxy 平面对称,则:
- 若 \(\Omega = \Omega_3 + \Omega_4\),且 \(\Omega_3, \Omega_5\) 关于 Oyz 平面对称,则:
- 若 \(\Omega = \Omega_5 + \Omega_6\),且 \(\Omega_5, \Omega_6\) 关于 Ozx 平面对称,则:
分两种情况,原理同上,故不再详细讨论。
应用⚓︎
设密度函数 \(\rho = \mu(P) = \mu(x, y, z)\) 连续,求空间闭形体 \(\Omega \subset \bm{R}^3\) 的质心坐标,设为 \((\overline{x}, \overline{y}, \overline{z})\)。
总质量 \(M = \int\limits_\Omega \mu (P) \mathrm{d}\Omega\)
设 \(\Omega \subset \bm{R}^3\) 的密度函数 \(\rho = \mu(P)\) 连续,求该物体的动能和关于 L 轴的转动惯量。
若 \(\Omega \subset \mathbf{R}^3\)(\(\Omega\) 是空间曲线 / 曲面 / 立体 )
- 当 L 是 Oz 轴时,\(I_z = \int\limits_\Omega (x^2 + y^2) \mu(P) \mathrm{d}\Omega = \int\limits_\Omega (x^2 + y^2) \mu(x, y, z) \mathrm{d}\Omega\)
- 当 L 是 Ox 轴时,\(I_x = \int\limits_\Omega (y^2 + z^2) \mu(P) \mathrm{d}\Omega = \int\limits_\Omega (y^2 + z^2) \mu(x, y, z) \mathrm{d}\Omega\)
- 当 L 是 Oy 轴时,\(I_y = \int\limits_\Omega (z^2 + x^2) \mu(P) \mathrm{d}\Omega = \int\limits_\Omega (z^2 + x^2) \mu(x, y, z) \mathrm{d}\Omega\)
若 \(\Omega \subset \mathbf{R}^2\)(\(\Omega\) 是平面曲线或平面区域 )
- 当 L 是 Ox 轴时,\(I_x = \int\limits_{\Omega}y^2 \mu(P)\mathrm{d}\Omega = \int\limits_\Omega y^2 \mu(x, y) \mathrm{d}\Omega\)
- 当 L 是 Oy 轴时,\(I_y = \int\limits_{\Omega}x^2 \mu(P)\mathrm{d}\Omega = \int\limits_\Omega x^2 \mu(x, y) \mathrm{d}\Omega\)
设 \(\Omega \subset \bm{R}^3\),\(\Omega\) 的密度函数 \(\rho = \mu(P) = \mu(x, y, z)\) 连续,\(P_0(x_0, y_0, z_0)\) 是一质点,质量为 m,求 \(\Omega\) 对质点 \(P_0\) 的引力。
- \(F_x = Gm\int\limits_\Omega \dfrac{\mu(P)(x - x_0)}{r^3}\mathrm{d}\Omega\)
- \(F_y = Gm\int\limits_\Omega \dfrac{\mu(P)(y - y_0)}{r^3}\mathrm{d}\Omega\)
- \(F_z = Gm\int\limits_\Omega \dfrac{\mu(P)(z - z_0)}{r^3}\mathrm{d}\Omega\)
评论区