Generative Models⚓︎

约 5368 个字 45 行代码预计阅读时间 27 分钟

Supervised vs Unsupervised Learning⚓︎

监督学习(supervised learning)：
- 数据：(x, y)，其中 x 是数据，y 是标签
- 目标：习得一个 x -> y 的函数
例子

分类 (classification) 图像描述 (image captioning) 目标检测 (object detection) 语义分割 (semantic segmentation)
无监督学习(unsupervised learning)：
- 数据：x（只有数据，没有标签）
- 目标：习得数据背后的隐藏结构
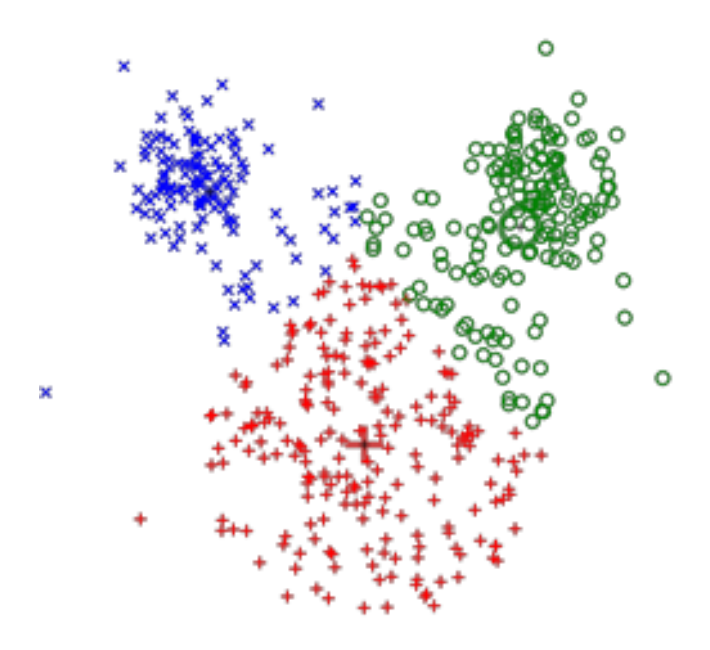
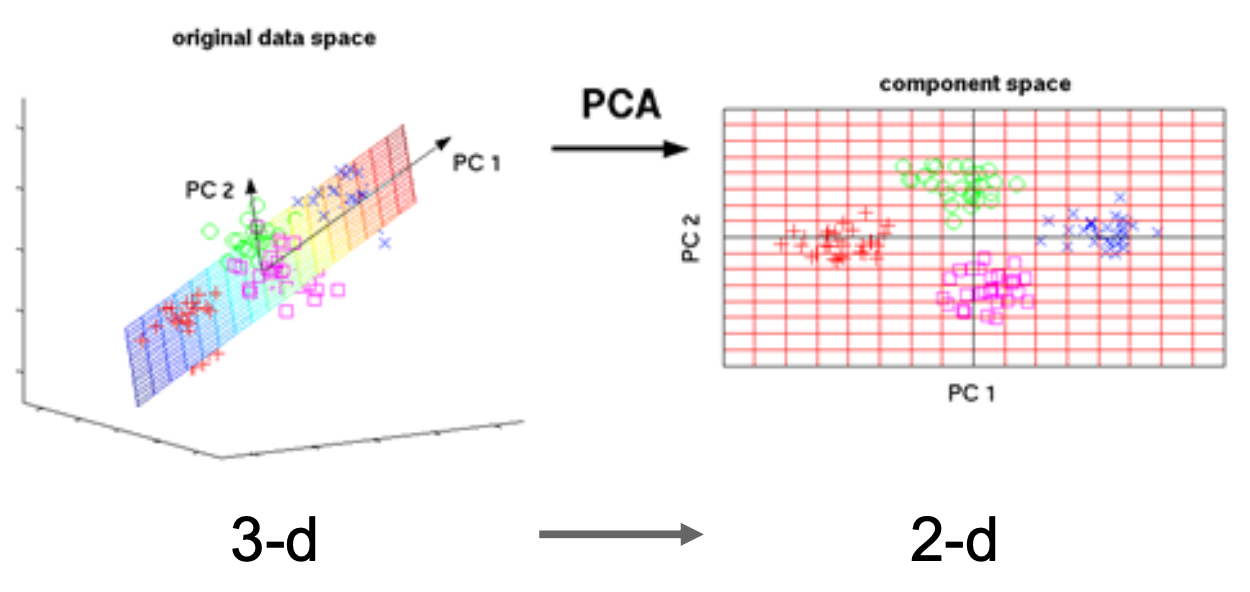
- 例子：聚类、、特征学习、密度估计等
例子

K 均值聚类 (K-means clustering) 主成分分析 (principal component analysis)（降维 (dimensionality reduction)）密度估计 (density estimation)

Generative vs Discriminative Models⚓︎

约定

$x$ 为数据， $y$ 为标签
回顾：
- 概率密度函数的归一化性质：$\int_X p(x) dx = 1$
- 贝叶斯定理：$P(x|y) = \dfrac{P(y|x)}{P(y)} P(x)$

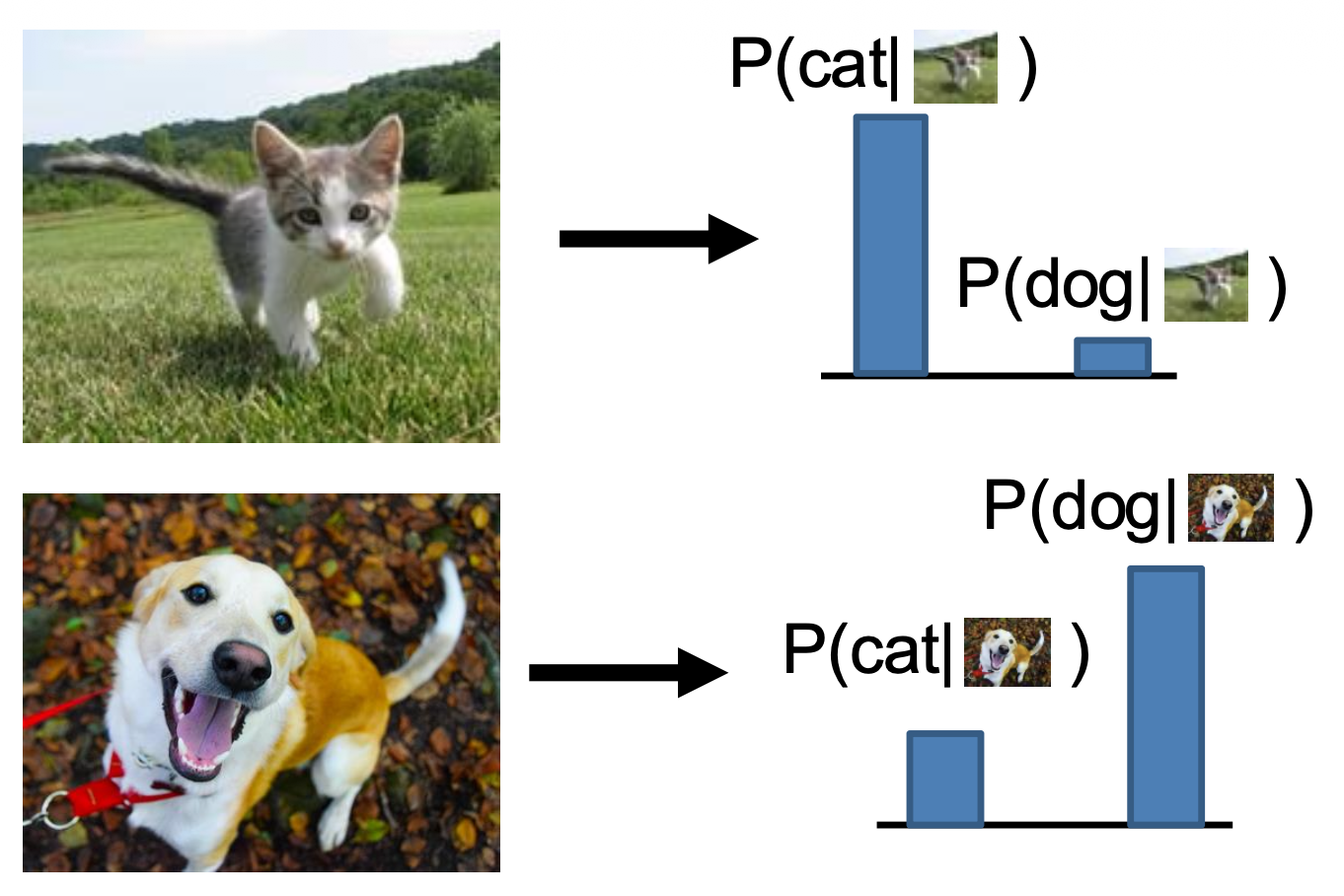
确定型模型(discrimitive model)：习得概率分布 $p(y|x)$
- 每张图片的可能标签在概率上相互竞争，而图片之间无竞争
- 无法处理不合理的输入，必须为所有可能的输入提供标签的分布
- 将标签赋予数据 ->（带标签的）特征学习
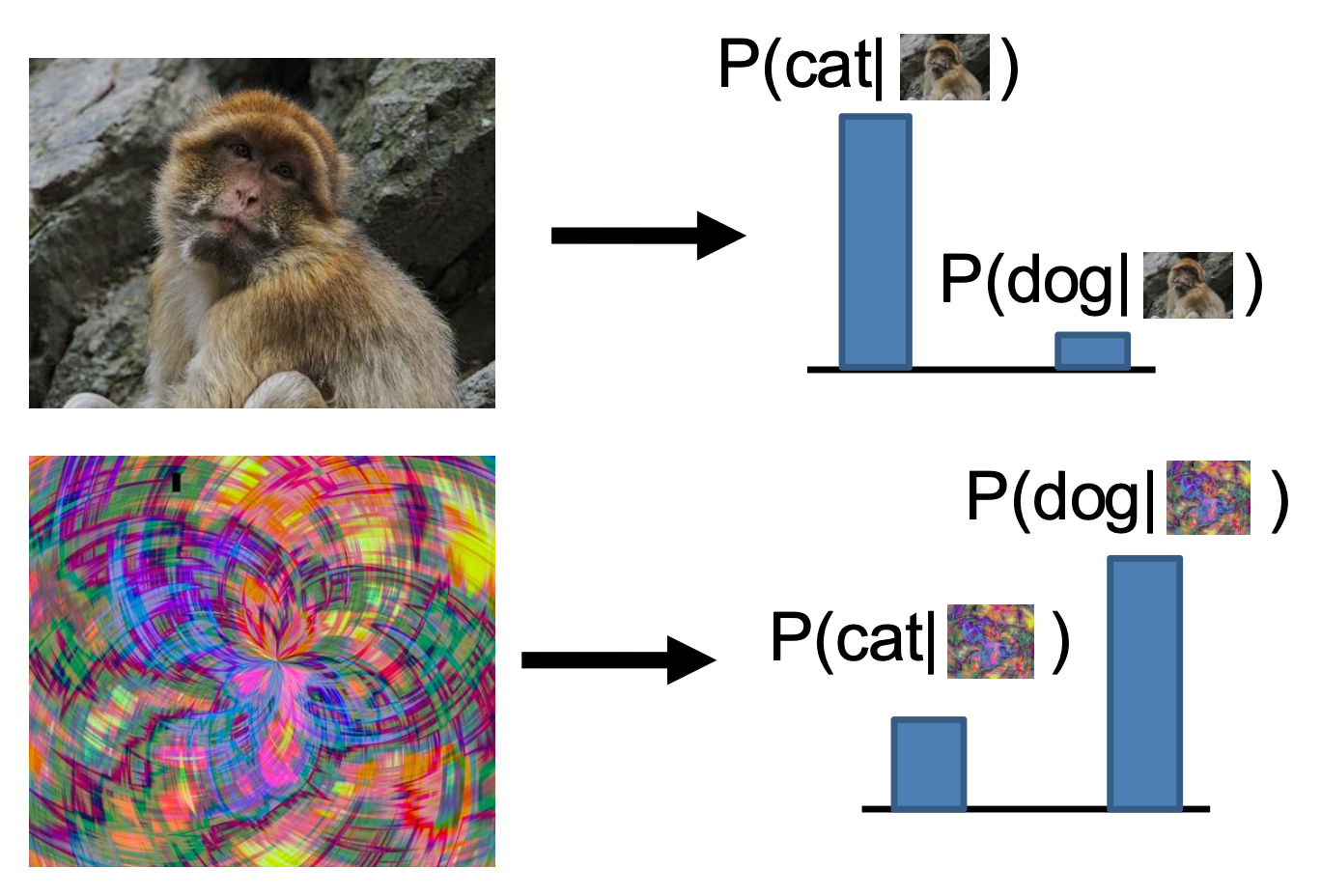
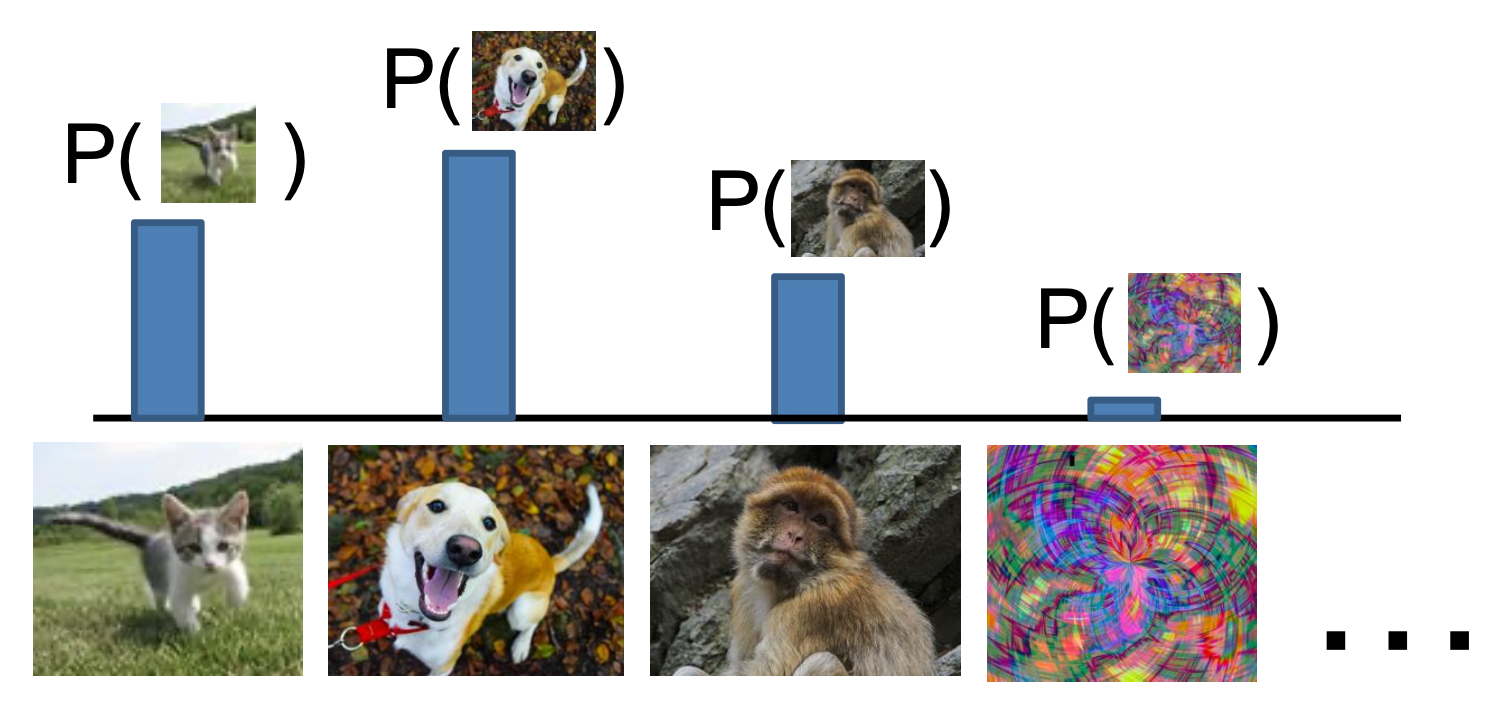
生成式模型(generative model)：习得概率分布 $p(x)$
- 所有可能的图像都将争夺概率
- 需要对图像有深度的理解：比如狗是坐着还是站着，3 条腿的狗是否比 3 条手臂的猴子更多（？）
- 通过给定很小的概率值来“拒绝”不合理的输入
- 检测异常点 ->（无标签的）特征学习，采样以生成最新的数据
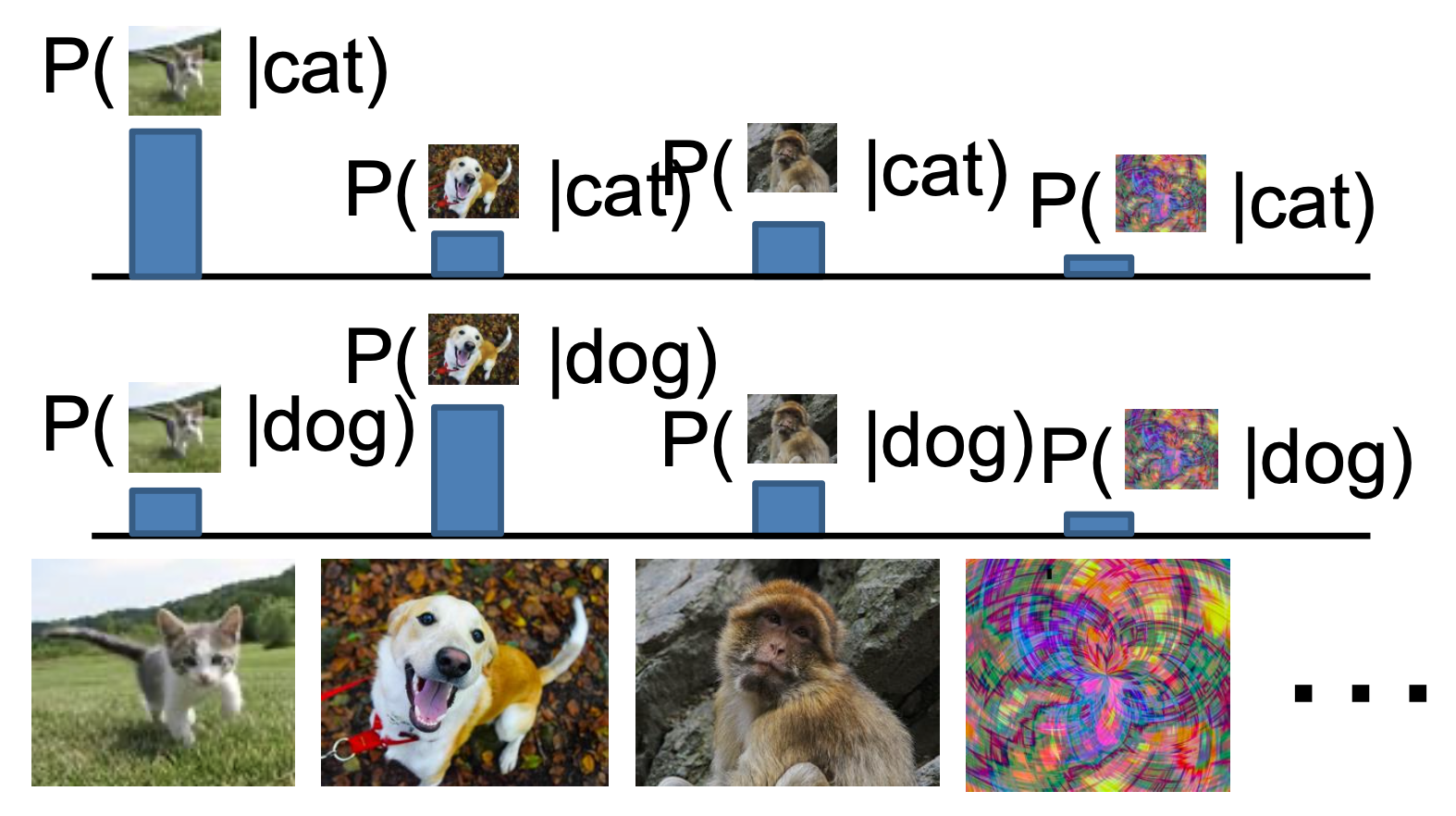
条件生成式模型(conditional generative model)：习得 $p(x|y)$
- 每个可能的标签在所有可能的图像中引发竞争
- 根据贝叶斯定理，可以根据上面两个模型构造条件生成式模型，但实际上这种做法并不常见
- 赋予标签的同时拒绝异常点
- 采样以根据标签生成数据

后两个模型都属于生成式模型，且后者在实际中最为常用。

Why Generative Models?⚓︎

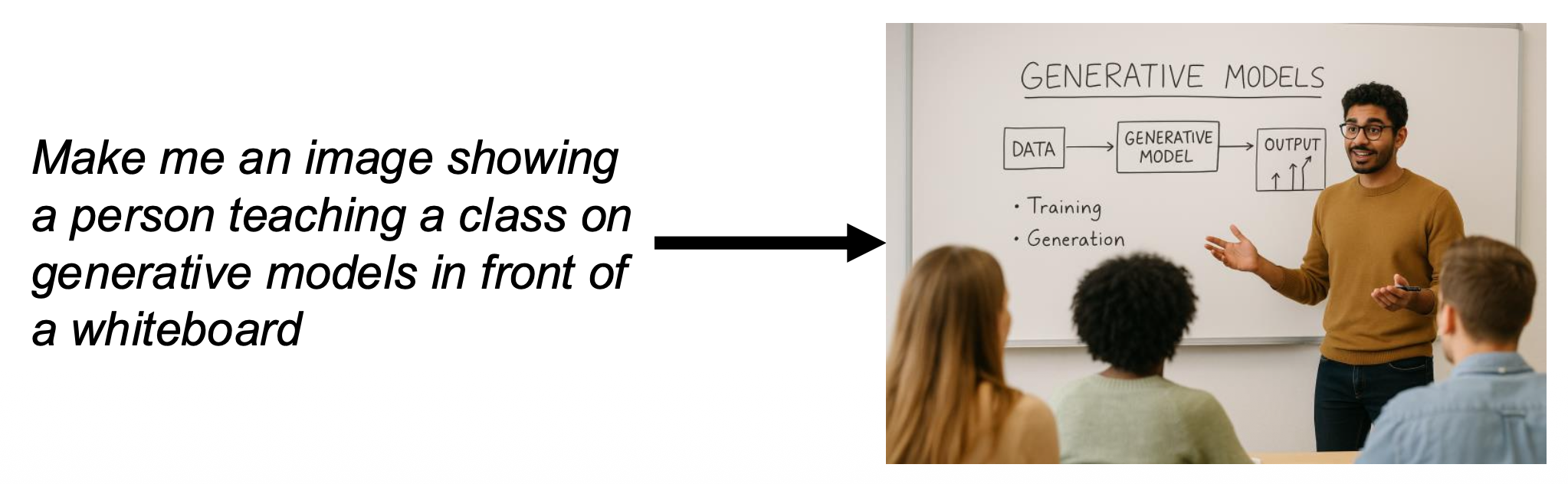
使用生成式模型的主要原因是建模模糊性(modeling ambiguity) 的特性：对于输入 $y$，有许多可能的输出 $x$（其概率为 $P(x|y)$）。基于这一特性，生成式模型有以下常见应用：

语言建模(language modeling)：根据输入文本 $y$ 输出文本 $x$
文生图(text to image)：根据输入文本 $y$ 输出图像 $x$
图生视频(image to video)：预测接下来发生什么

生成式模型的分类 (taxonomy)

Autoregressive Models⚓︎

Maximum Likelihood Estimation⚓︎

自回归模型(autoregressive models) 的目标是：写下一个显式函数 $p(x) = f(x, W)$

对于给定数据集 $x^{(1)}, x^{(2)}, \dots, x^{(N)}$，通过解以下方程来训练模型：

\[ \begin{aligned} W^{*} &= \arg \max_{W} \prod_{i} p(x^{(i)}) \\ &= \arg \max_{W} \sum_{i} \log p(x^{(i)}) \\ &= \arg \max_{W} \sum_{i} \log f(x^{(i)}, W) \end{aligned} \]

第一行：最大化训练数据的概率（最大似然估计(maximum likelihood estimation)）
第二行：对数技巧：乘积 -> 求和
第三行：最终的损失函数，使用梯度下降将其最大化

Autoregressive Models⚓︎

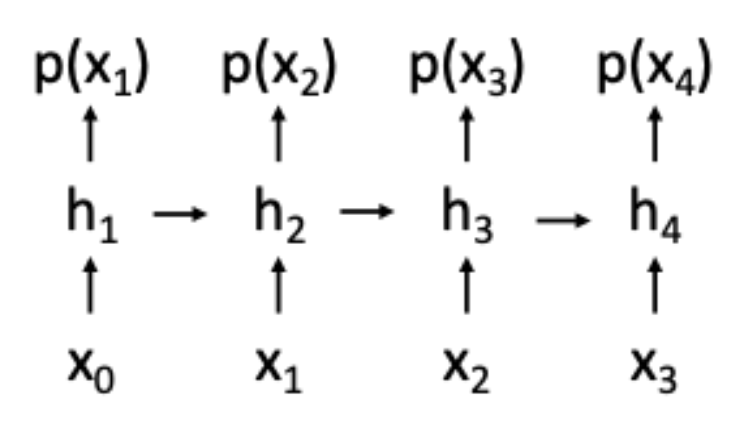
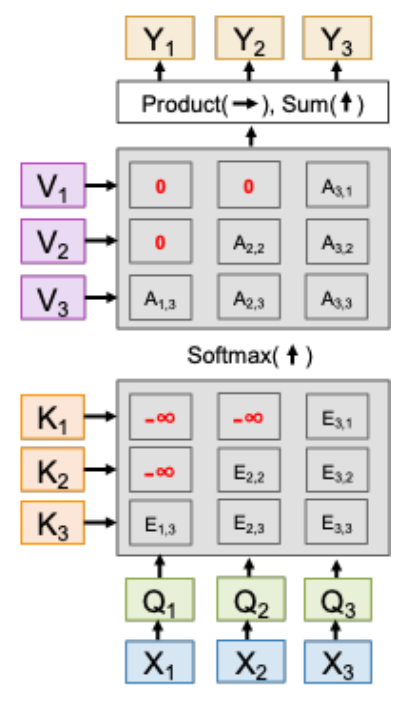
假设 $x$ 是一个序列，即 $x = (x_1, x_2, \dots, x_T)$，那么可以使用概率的链式法则求解：

\[ \begin{aligned} p(x) &= p(x_{1}, x_{2}, x_{3}, ..., x_{T}) \\ &= p(x_{1}) p(x_{2} \mid x_{1}) p(x_{3} \mid x_{1}, x_{2}) \dots \\ &= \prod_{t=1}^{T} p(x_{t} \mid x_{1}, \dots, x_{t-1}) \end{aligned} \]

这和 RNN 的思路很像，也和掩码 Transformer 很像。

RNN
掩码 Transformer

Autoregressive Models of Images⚓︎

将图像看作一个包含多个 8 位子像素(subpixel) 值的序列（按扫描顺序）
将每个子像素预测为在 256 个值 [0 ... 255] 中的分类
使用 RNN 或 Transformer 建模
问题：成本太高，比如 1024x1024 的图像就是一个包含 3M 个子像素的序列
解决方法：将图像看作由块(tile) 构成的序列

Variational Autoencoders (VAEs)⚓︎

PixelRNN / PixelCNN 明确地用神经网络参数化密度函数，因此我们可以通过训练来最大化训练数据的似然性： $$ p_W(x) = \prod_{t=1}^T p_W(x_t | x_1, \dots, x_{t-1}) $$

变分自编码器(variational autoencoders, VAE) 定义了一种不可处理的(intractable)密度（无法显式计算或优化）。但我们能直接优化密度的下界。

Autoencoders (AEs)⚓︎

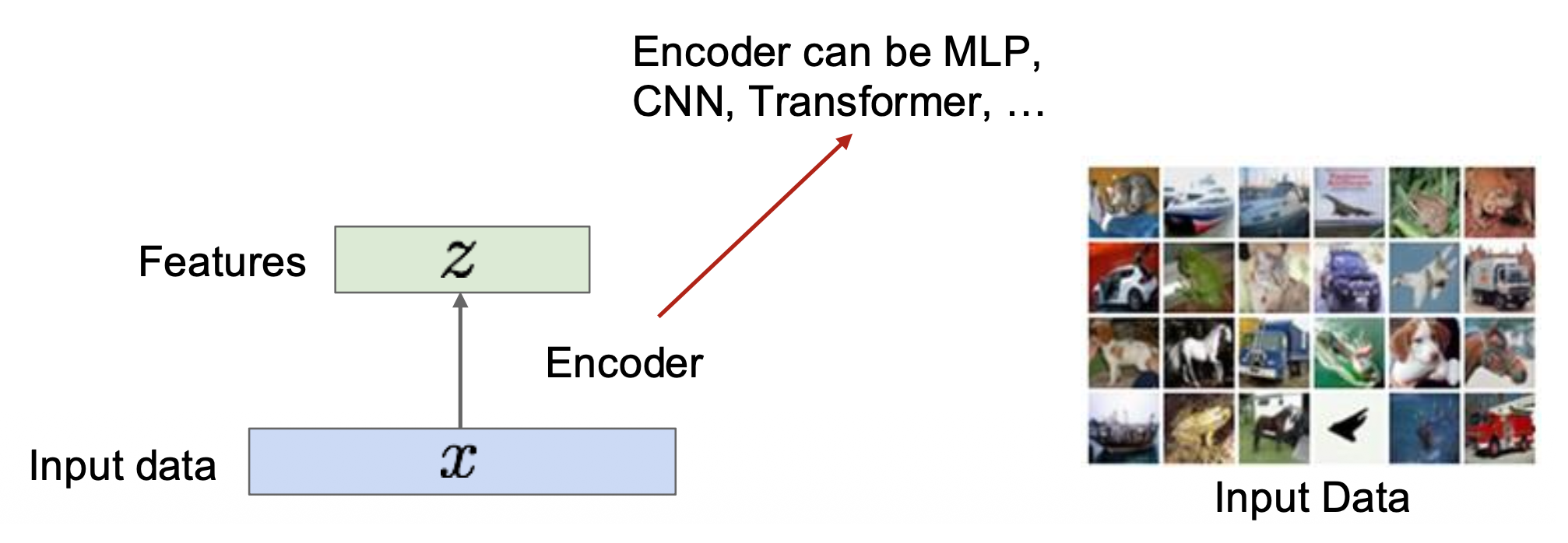
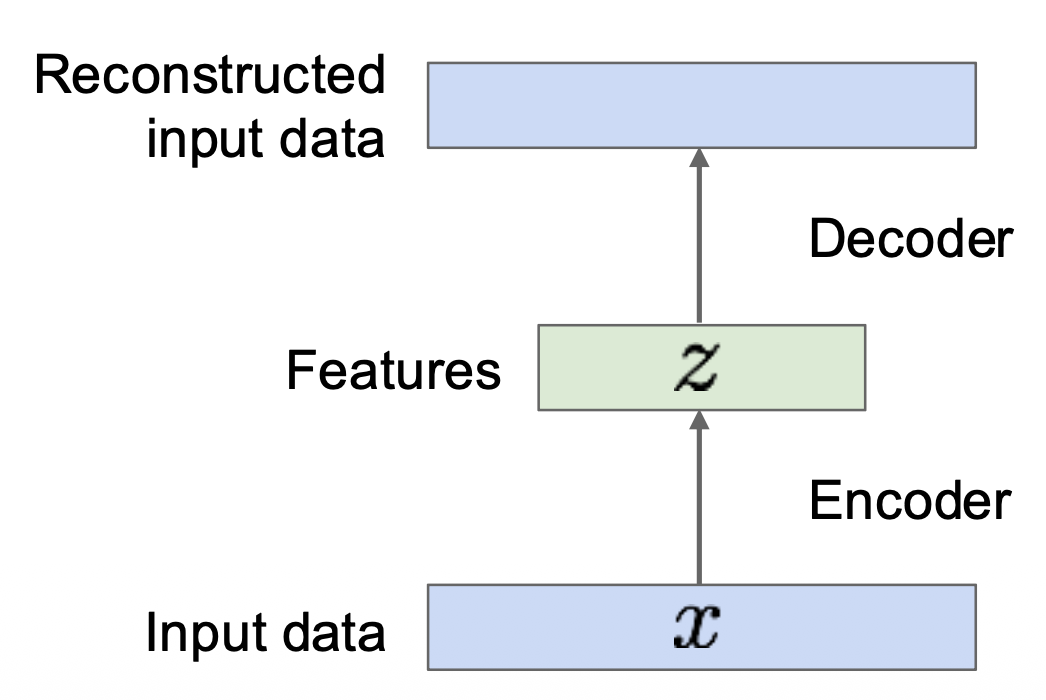
（非变分）自编码器的思路是通过无监督方法学习从无标签的输入 x 中提取特征 z。

特征应当能提取能被用在下游任务中的有用信息（比如目标身份、外观、场景类型等）。

思考

问题解答

如何在无标签的情况下学习？

使用解码器(decoder) 重建输入数据；解码器可以是 MLP，CNN 或 Transformer。

损失用输入数据 $x$ 和重建数据 $\hat{x}$ 的 L2 距离衡量，即 $\|\hat{x} - x\|_2^2$。

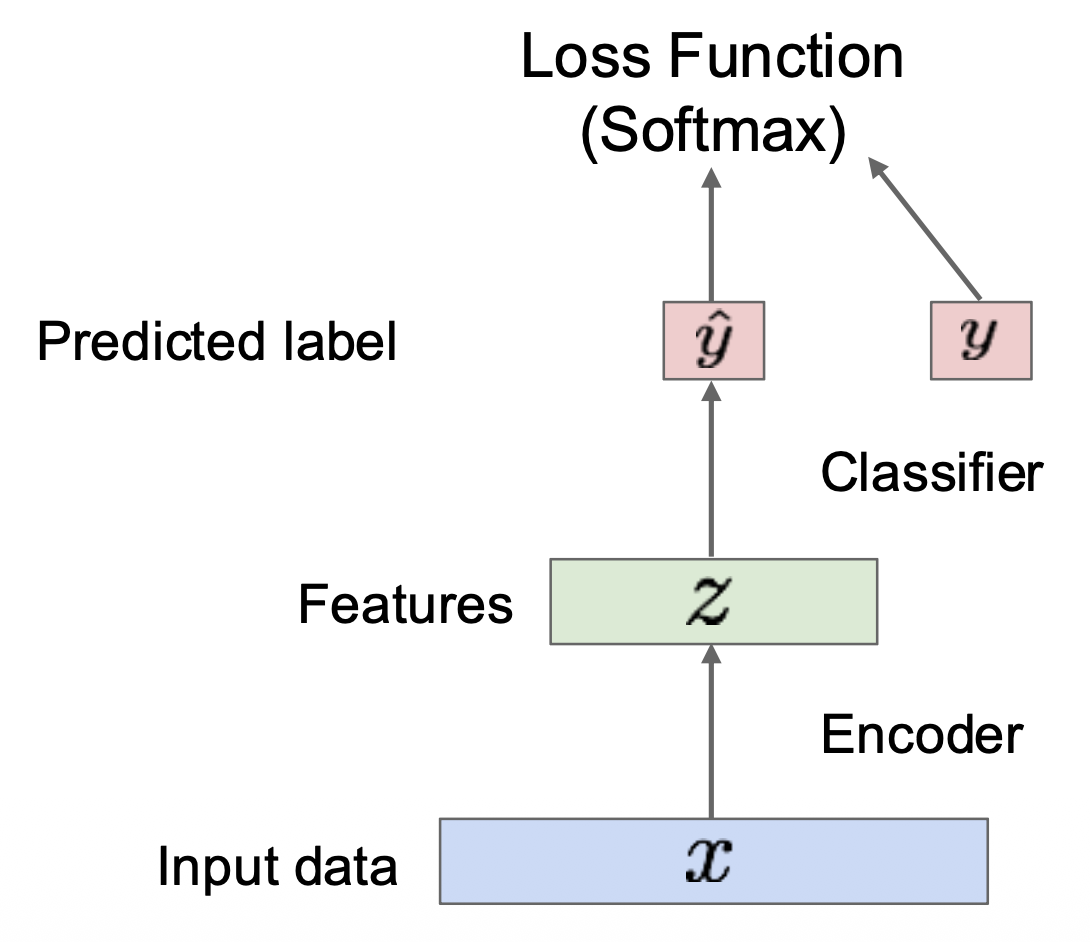
训练后，使用编码器，用于下游任务中：

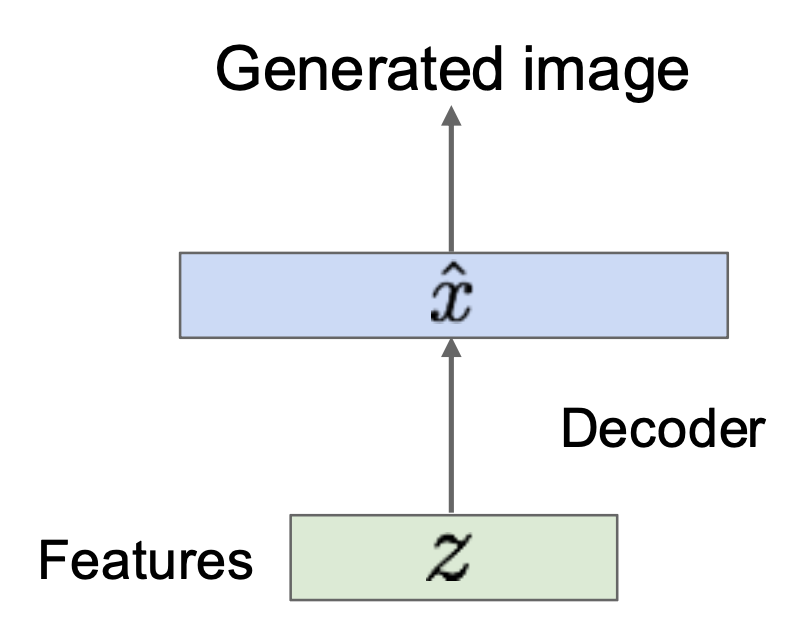
如果能生成新的 $z$，那就能用解码器来生成图像了。

但问题是生成新的 $z$ 不会比生成新的 $x$ 容易。解决方案是强迫所有 $z$ 来自一个已知的分布。

Variational Autoencoders (VAEs)⚓︎

从原始数据习得潜在特征(latent feature) $z$
从模型中采样以得到新的数据

假设训练数据 $\{x^{(i)}\}_{i=1}^N$ 生成自未观察到的（潜在）表示 $z$。直觉上看，若 $x$ 是一张图像，那么 $z$ 就是用于生成 $x$ 的潜在因子，比如属性、方向等。

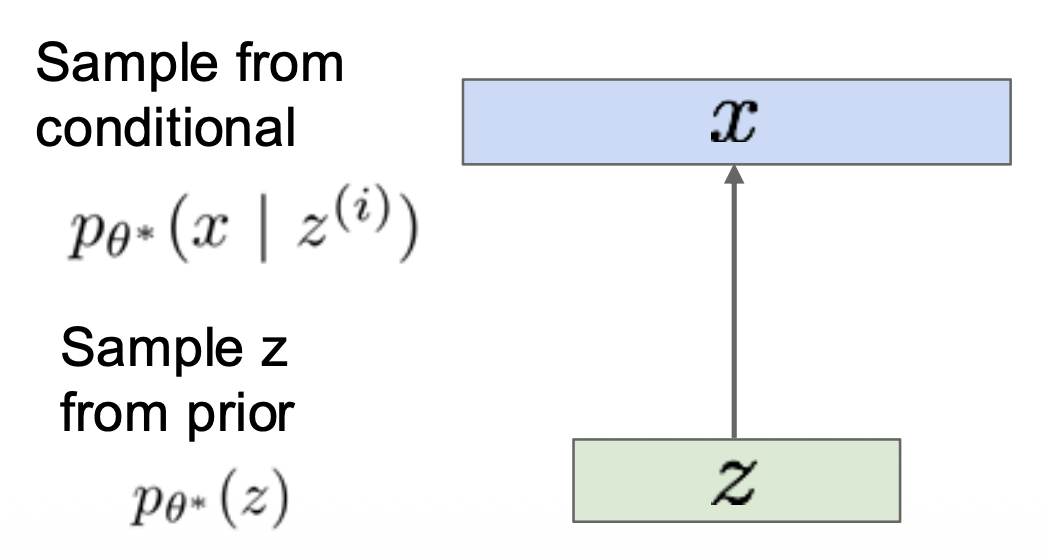
训练后，像这样采样新的数据：

对于下半部分（绿色），假设是简单的先验概率 $p(z)$，比如高斯分布
对于上半部分（蓝色）
- 训练的基本思想依然是最大似然
- 若有关于 $(x, z)$ 的数据集，那么训练一个条件生成式模型 $p(x|z)$
- 我们没有观察 $z$，因此进行边缘化(marginalize)：
  
  \[ p_\theta (x) = \int p_\theta (x, z) dz = \int p_\theta (x|z) p_\theta (z) dz \]
  - 其中 $p_\theta (x|z)$ 能用解码器计算出来，$p_\theta (z)$ 已经假设为高斯先验概率
  - 问题：我们无法对所有的 $z$ 积分
- 尝试另一个思路：贝叶斯定理
  
  \[ p_\theta (x) = \dfrac{p_\theta (x|z) p_\theta (z)}{p_\theta (z|x)} \]
  - 但 $p_\theta (z|x)$ 没法算出来
  - 解决思路：训练另一个网络，得到 $q_\phi (z|x) \approx p_\theta (z|x)$

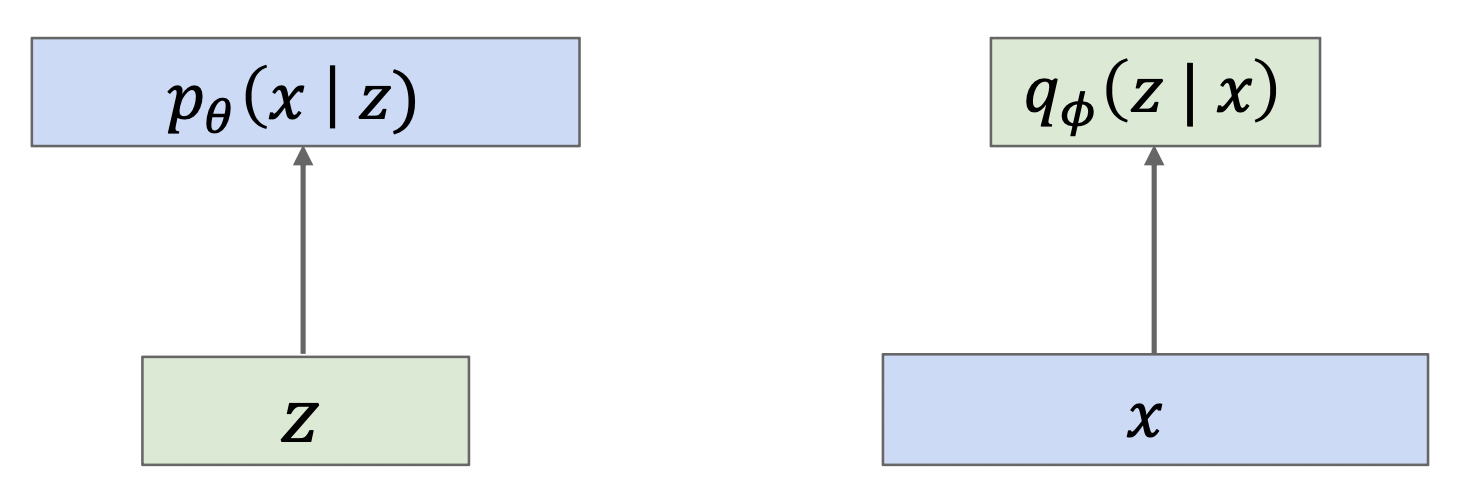
于是，整个 VAE 分为两个部分：

解码器网络：输入潜在编码 $z$，输出关于数据 $x$ 的分布（左图）
编码器网络：输入数据 $x$，输出关于潜在编码 $z$ 的分布（右图）

如果能确保 $q_\phi (z|x) \approx p_\theta (z|x)$，那么我们就能近似表示 $p_\theta (x)$，即：

\[ p_\theta (x) = \dfrac{p_\theta (x|z) p_\theta (z)}{q_\phi (z|x)} \]

所以现在的思路是：联合训练编码器和解码器。

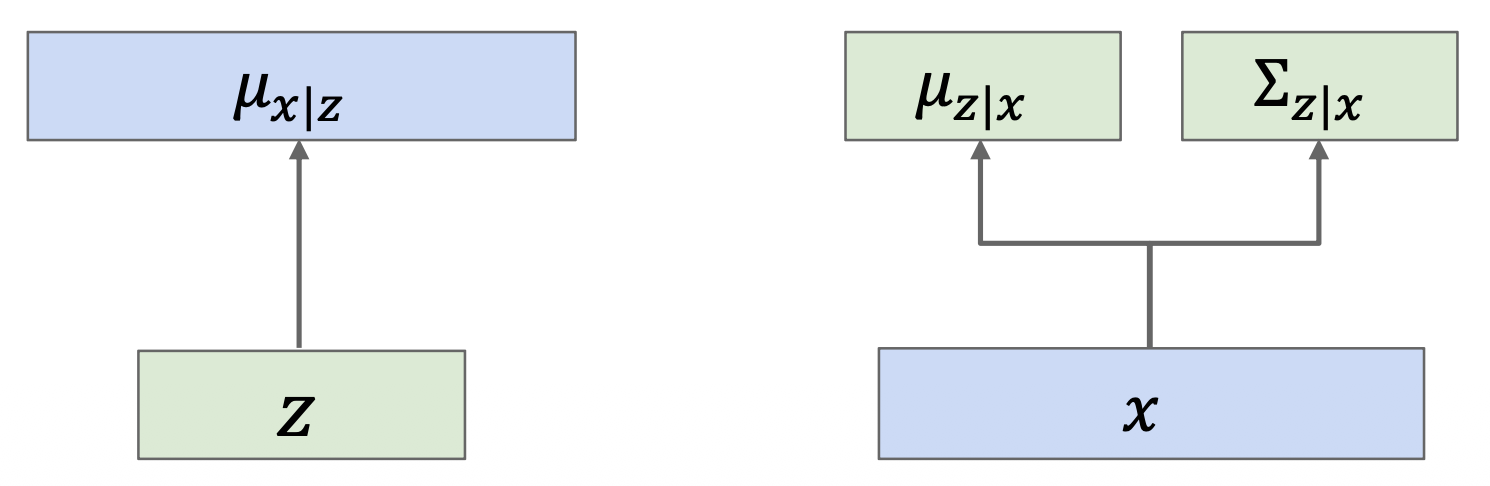
神经网络是通过输出（对角线）分布的均值（和标准差）来输出概率分布的，因此将上图转变为以下形式：

$p_\theta (x|z) = N(\mu_{x|z}, \sigma^2)$ -> $\log p_\theta (x|z) = -\dfrac{1}{2\sigma^2} \|x - \mu\|_2^2 + C_2$
$q_\phi (z|x) = N(\mu_{z|x}, \Sigma_{z|x})$

不难发现，最大化 $\log p_\theta (x|z)$ 等价于最小化 $x$ 和网络输出的 L2 距离。

继续计算 $\log p_\theta (x|z)$：

\[ \begin{aligned} \log p_\theta(x) & = \log\dfrac{p_\theta (x|z) p_\theta (z)}{p_\theta (z|x)} = \log \dfrac{p_\theta (x|z) p_\theta (z) q_\phi (z|x)}{p_\theta (z|x) q_\phi (z|x)} \\ & = \log p_\theta(x|z) - \log \dfrac{q_\phi(z|x)}{p(z)} + \log \dfrac{q_\phi(z|x)}{p_\theta(z|x)} \end{aligned} \]

由于上式不依赖于 $z$，因此可以将其包装成期望的形式，即： $$ \begin{aligned} \log p_\theta(x) & = E_{z \sim q_\phi(z|x)}[\log p_\theta (x)] \ & = E_z[\log p_\theta(x|z)] - E_z \left[\log \dfrac{q_\phi(z|x)}{p(z)}\right] + E_z \left[\log \dfrac{q_\phi(z|x)}{p_\theta(z|x)} \right] \ & = E_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)] - D_{KL}(q_{\phi}(z|x), p(z)) + D_{KL}(q_{\phi}(z|x), p_{\theta}(z|x)) \end{aligned} $$

最后三项分别代表：

数据重建(data reconstruction)：
- x => 解码器 => 编码器的过程应该能重建 x
- 计算得到关于高斯分布的封闭形式
先验概率(prior)：
- 编码器的输出 $q_{\phi}(z|x)$ 需要和关于 z 的先验概率 $p(z)$ 匹配
- 计算得到关于高斯分布的封闭形式
后验近似(posterior approximation)：
- 编码器的输出 $q_{\phi}(z|x)$ 需要和 $p_{\theta}(z|x)$ 匹配
- 无法进行关于高斯分布的计算
- 解码器的输出 $q_{\phi}(z|x)$ 需要和 $p_{\theta}(z|x)$ 匹配
- 由于 KL >= 0，所以我们可以删除这项，获取似然的下限

综上，我们的 VAE 的训练目标为：

\[ \log p_{\theta}(x) \geq E_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)] - D_{KL}(q_{\phi}(z|x), p(z)) \]

像这种共同训练编码器 q 和解码器 p，以最大化数据似然的变分下界，也称为证据下界(evidence lower bound, ELBo)。

Training⚓︎

训练步骤如下：

通过编码器运行输入数据，以得到关于 $z$ 的概率分布
先验损失：编码器输出应该是单位高斯（标准正态分布，均值为 0，单位方差）
从编码器输出 $q_\phi (z|x)$ 中采样 $z$（重参数化 (reparameterization) 技巧）
通过解码器运行 $z$，得到预测的数据均值
重建损失：预测均值需要在 L2 上和 $x$ 匹配

损失项之间处于相互抗争的状态：

重建损失（$E_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)]$）希望 $\Sigma_{z|x} = 0$ 且 $\mu_{z|x}$ 对每个 $x$ 而言是唯一的，因此解码器能确定得重建 $x$
先验损失（$D_{KL}(q_{\phi}(z|x), p(z))$）希望 $\Sigma_{z|x} = \mathbf{I}$ 且 $\mu_{z|x} = 0$，因此编码器输出始终遵循标准正态分布

Sampling⚓︎

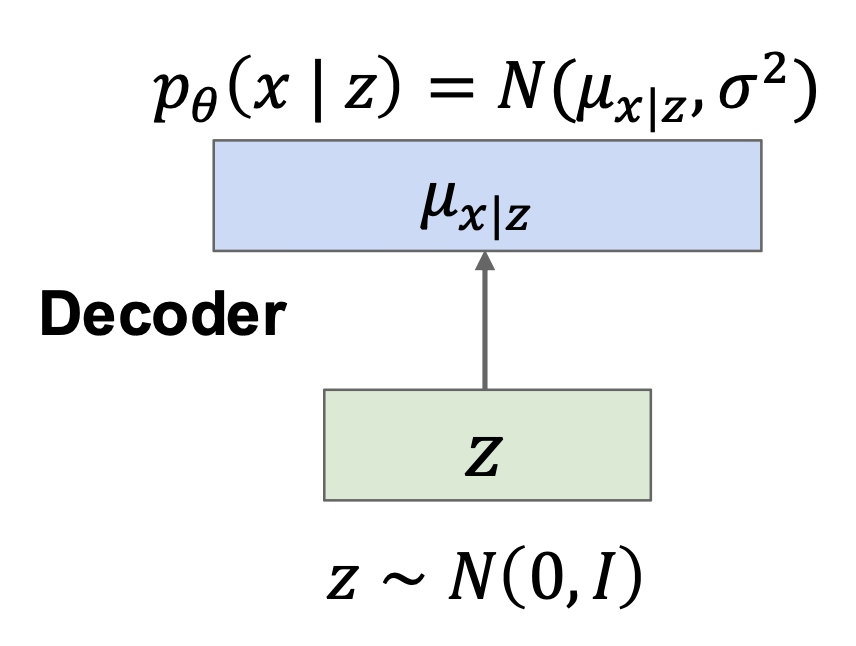
采样步骤如下：

从先验分布中采样 $z$
运行解码器以获取图像

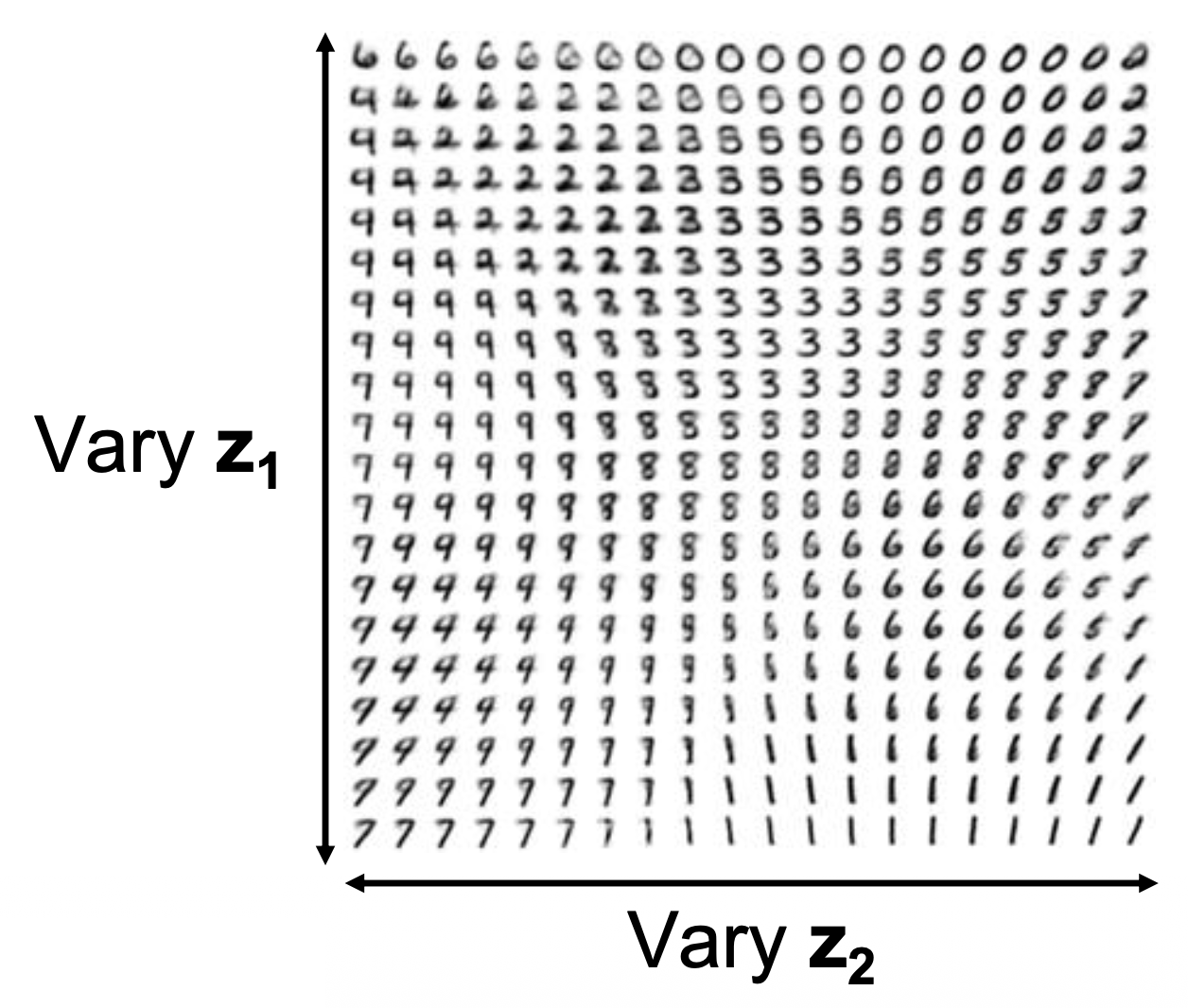
Disentangling⚓︎

$p(z)$ 的对角先验分布导致 $z$ 的维度相互独立
“解耦变化因素 (disentangling factors of variation)”

Generative Adversarial Networks⚓︎

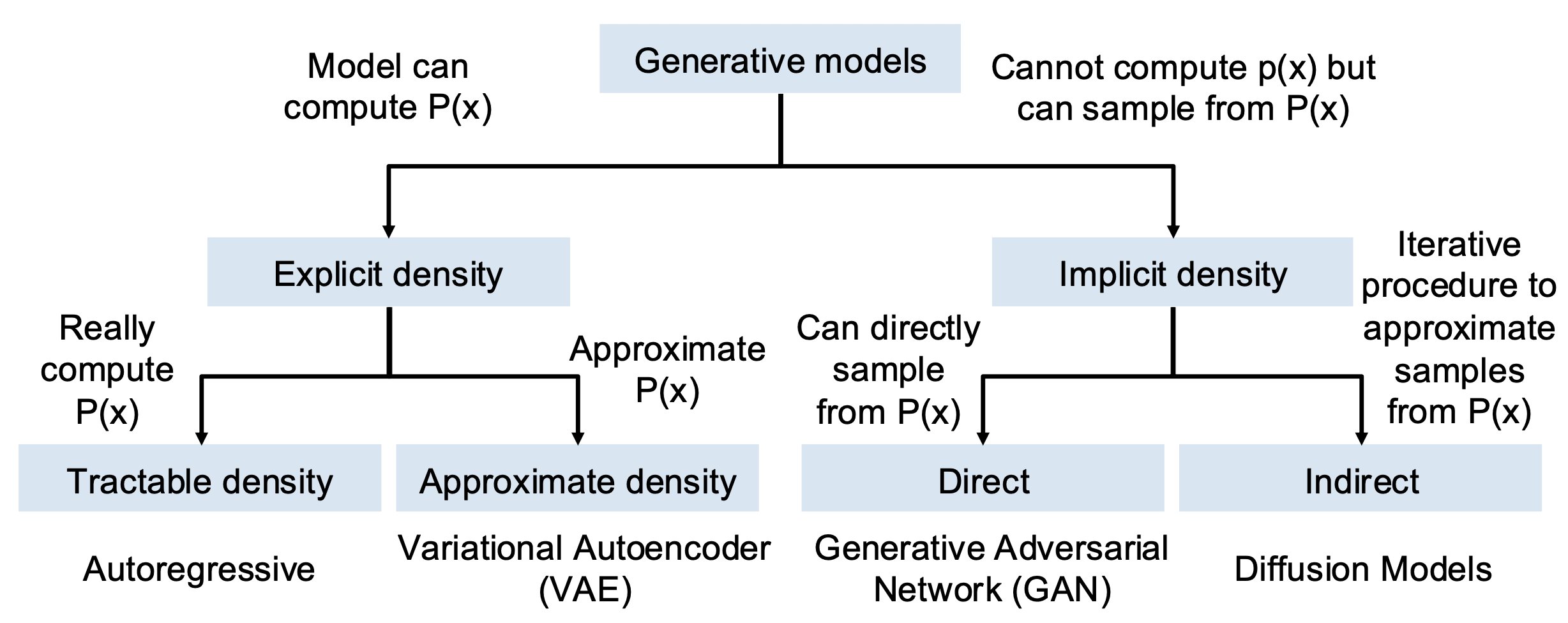
回顾目前学过的生成式模型

自回归模型直接最大化训练数据的似然

\[ p_{\theta}(x) = \prod_{i=1}^{N} p_{\theta}(x_i | x_1, \dots, x_{i-1}) \]
变分自编码器引入潜在特征 $z$，并最大化下限

\[ p_{\theta}(x) = \int_{z} p_{\theta}(x|z)p(z)dz \geq \mathbb{E}_{z \sim q_{\phi}(z|x)}[\log p_{\theta}(x|z)] - D_{KL}(q_{\phi}(z|x), p(z)) \]

生成式对抗网络(generative adversarial network, GAN) 放弃对 $p(x)$ 建模，而是允许我们根据 $p(x)$ 抽取样本。

设置：从分布 $p_{\text{data}}(x)$ 中抽取数据 $x_i$，想从 $p_{\text{data}}$ 中采样
思路：
- 引入潜变量 $z$，它具有简单的先验 $p(z)$（例如单位高斯分布）
- 从分布 $z \sim p(z)$ 采样，将其传递给生成器网络(generator network) $x = G(z)$；此时 $x$ 就是来自生成器分布 $p_G$ 的一个样本，我们希望 $p_G = p_{\text{data}}$

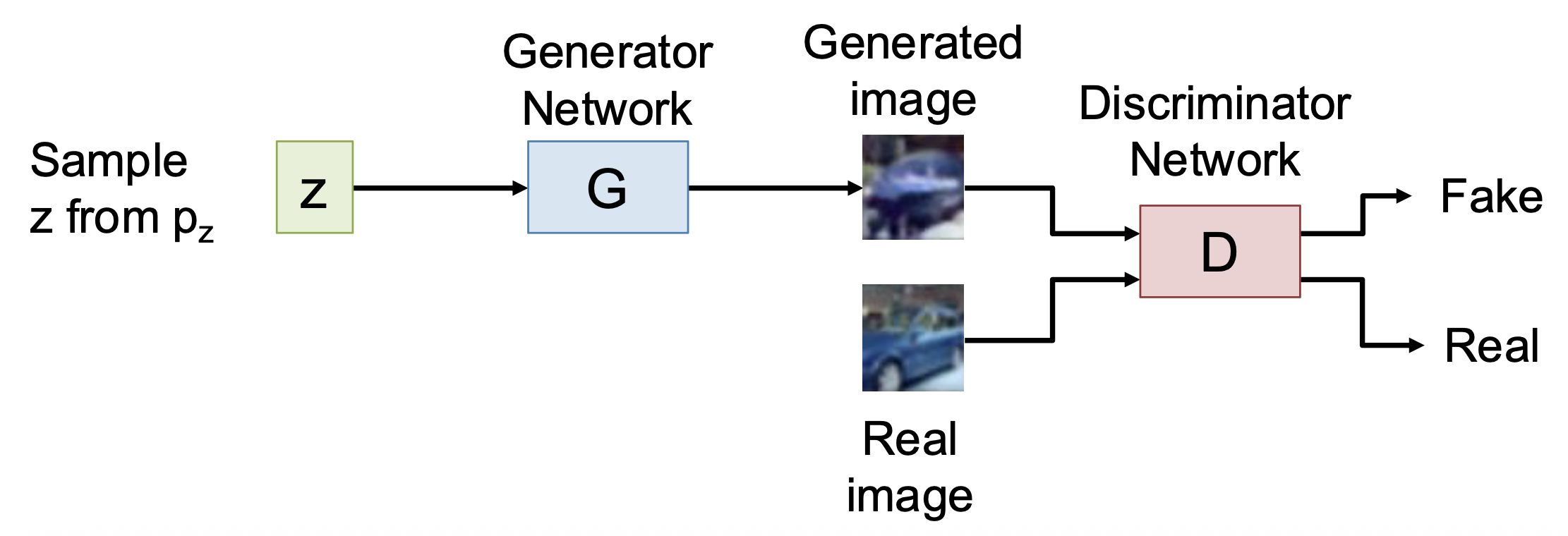
GAN 的架构图如下：

训练生成器网络 $G$，将 $z$ 转换从 $p_G$ 中采样得到的假数据 $x$，用于欺骗判别器 $D$
训练判别器网络(discriminator network) $D$ 来为数据的真假分类

Training Objective⚓︎

$G, D$ 应当共同训练，目标是让 $p_G$ 收敛于 $p_{\text{data}}$，即完成以下极小极大博弈(minimax game)（方程中的颜色和上图对应）： $$ \min_{\textcolor{cornflowerblue}{G}} \max_{\textcolor{red}{D}} \left( E_{x \sim p_{data}} [\log \textcolor{red}{D(}x\textcolor{red}{)}] + E_{\textcolor{yellowgreen}{z \sim p(z)}} [\log(1 - \textcolor{red}{D(}\textcolor{cornflowerblue}{G(}\textcolor{yellowgreen}{z}\textcolor{cornflowerblue}{)}\textcolor{red}{)})] \right) $$

其中：

$D(x) = P(x \text{ is real})$
- $D(x) = 0 \Rightarrow $ 假数据
- $D(x) = 1 \Rightarrow $ 真数据
训练 $D$ 时想象固定 $G$

\[ \min_{\textcolor{cornflowerblue}{G}} \max_{\textcolor{red}{D}} \left( \overbrace{E_{x \sim p_{data}} [\log \textcolor{red}{D(}x\textcolor{red}{)}]}^{\textcolor{red}{\substack{\text{Discriminator wants} \\ D(x) = 1\text{ for real data}}}} + E_{\textcolor{yellowgreen}{z \sim p(z)}} [\overbrace{\log(1 - \textcolor{red}{D(}\textcolor{cornflowerblue}{G(}\textcolor{yellowgreen}{z}\textcolor{cornflowerblue}{)}\textcolor{red}{)})}^{\textcolor{red}{\substack{\text{Discriminator wants} \\ D(x) = 0\text{ for fake data}}}}] \right) \]
训练 $G$ 时想象固定 $D$

\[ \min_{\textcolor{cornflowerblue}{G}} \max_{\textcolor{red}{D}} \left( \overbrace{E_{x \sim p_{data}} [\log \textcolor{red}{D(}x\textcolor{red}{)}]}^{\textcolor{cornflowerblue}{\substack{\text{This term oes not} \\ \text{depend on } G}}} + E_{\textcolor{yellowgreen}{z \sim p(z)}} [\overbrace{\log(1 - \textcolor{red}{D(}\textcolor{cornflowerblue}{G(}\textcolor{yellowgreen}{z}\textcolor{cornflowerblue}{)}\textcolor{red}{)})}^{\textcolor{cornflowerblue}{\substack{\text{Generator wants} \\ D(x) = 1\text{ for fake data}}}}] \right) \]

具体来说，使用交替的梯度更新来训练 $G, D$。先将方程简写为 $\min\limits_G \max\limits_D V(G, D)$，那么：

while True:
    D = D + alpha_D * dV / dD
    G = G - alpha_G * dV / dG

注意

我们不是在最小化总体损失，并且没有可参考的训练曲线。

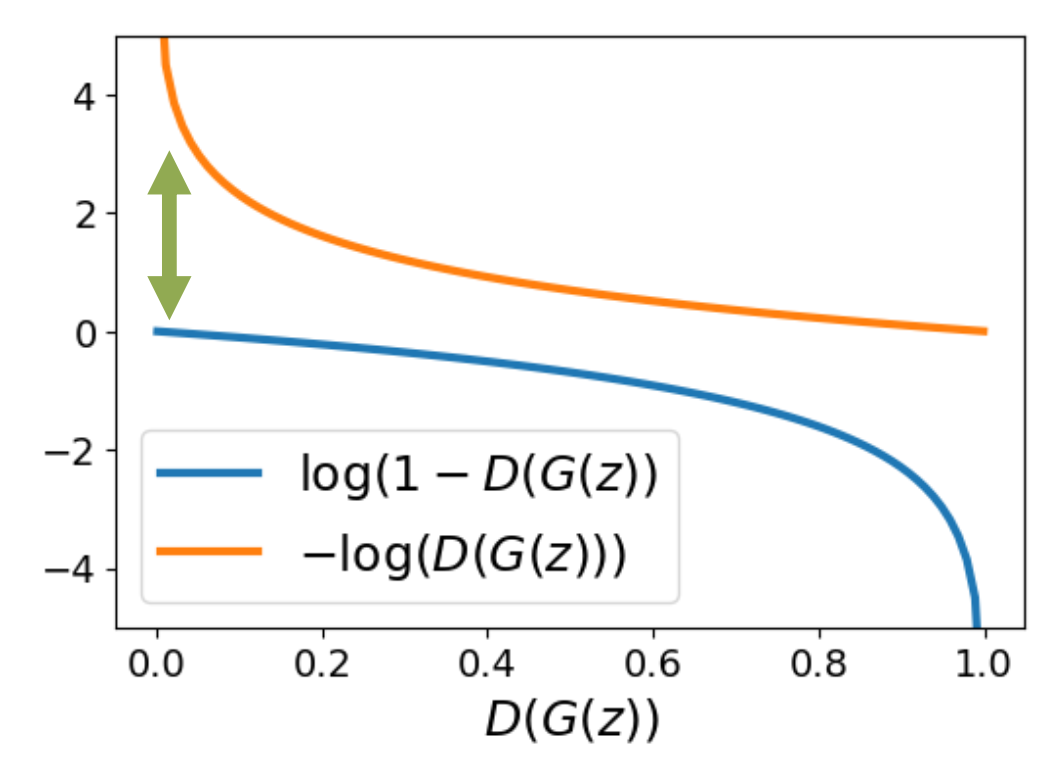
在训练开始时，生成器表现非常糟糕，而判别器能够轻松区分数据的真假，因此 $D(G(z))$ 的结果接近 0
问题：$G$ 的梯度接近 0，导致训练不起来
- 解决方案：生成器希望 $D(G(z)) = 1$，那就通过训练生成器以最小化 $-\log D(G(z))$，训练判别器以最大化 $\log (1 - D(G(z)))$，这样生成器在一开始获得很大的梯度

思考

问题解答

为何上述方程是一个好的目标函数？

内在目标通过以下方程最大化（对任何 $p_G$，证明略）：

\[ D_G^* (x) = \dfrac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_G(x)} \]
外在目标通过以下方程最小化：$p_G(x) = p_{\text{data}}(x)$

注意

具有固定容量的神经网络可能无法表示最优的 $D, G$，这并没有告诉我们关于有限数据解的收敛性的任何信息。

GAN Architecture⚓︎

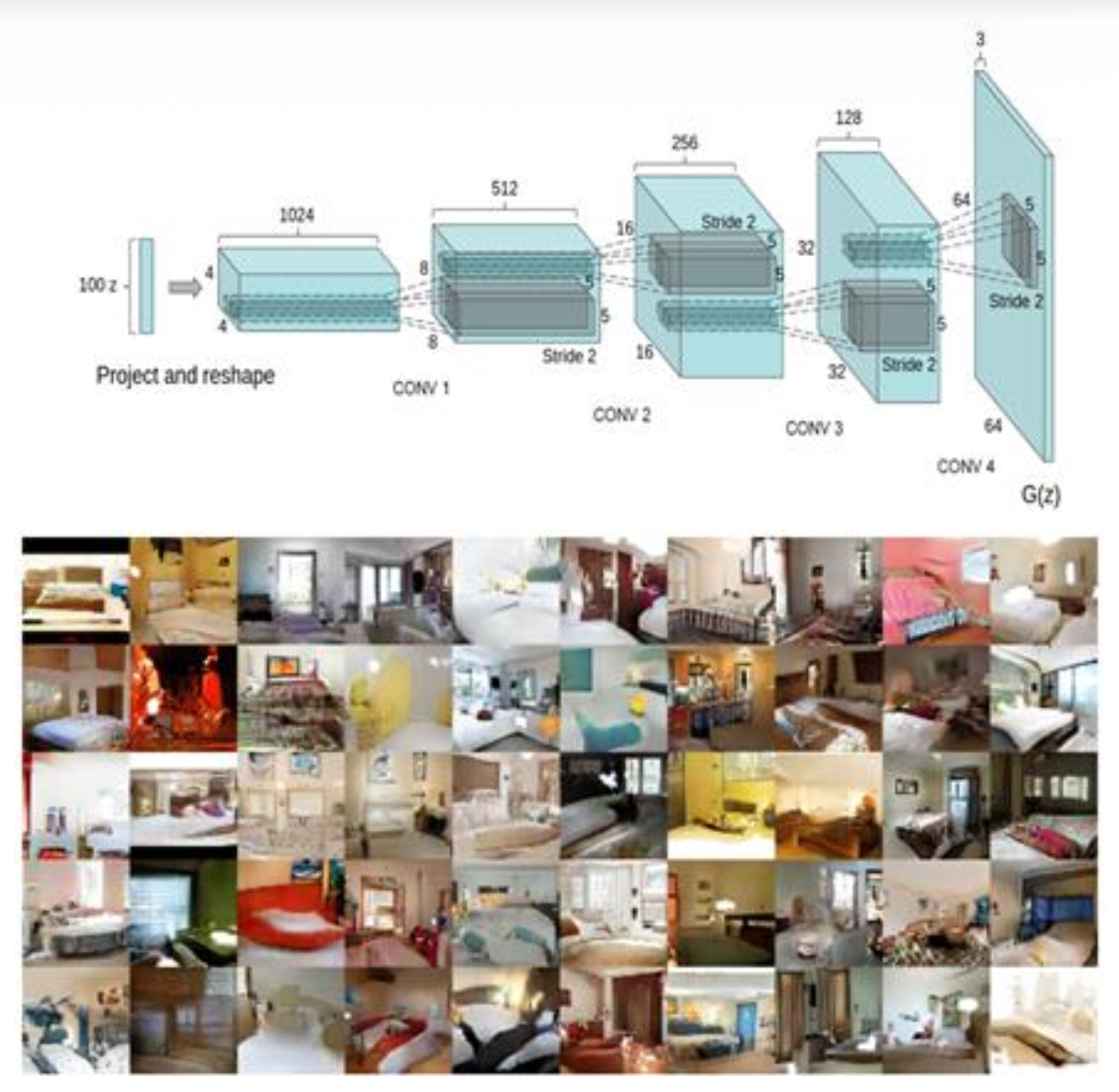
DC-GAN⚓︎

生成器和判别器都是神经网络
神经网络通常是 CNNs，在 Vit 诞生前 GAN 并不受欢迎
DC-GAN 是第一个在非玩具数据上运行的 GAN 架构

注：作者 Radford 后来参与了 GPT-1 和 GPT-2 的设计。

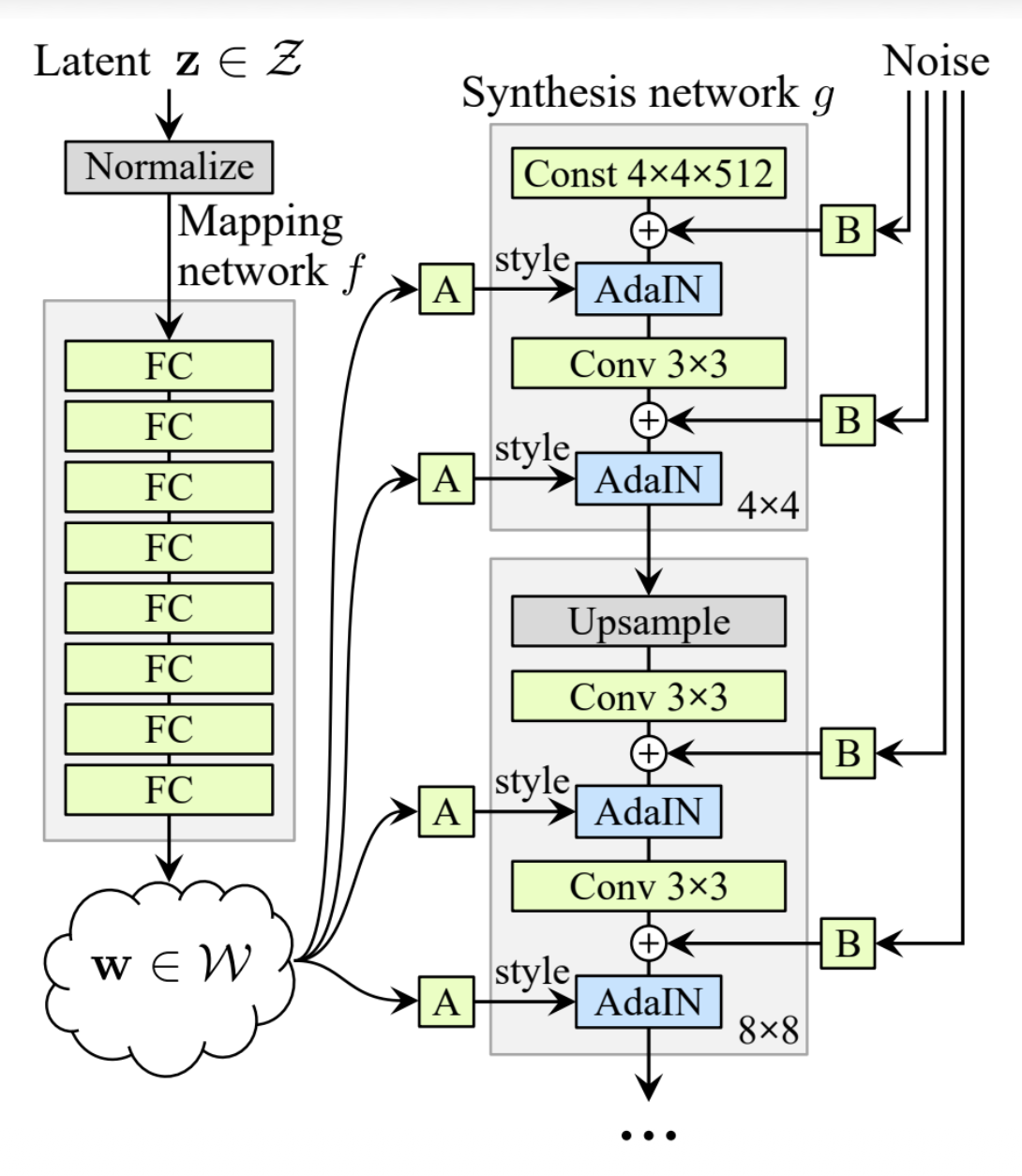
StyleGAN⚓︎

StyleGAN是一种更复杂的架构，它通过自适应归一化(adaptive normalization) 来注入噪音
在每一层预测一个与 $x$ 相同形状的缩放因子 $w$ 和偏移量 $b$：

\[ AdaIN(x, w, b)_w = w_i \dfrac{x_i - \mu(x)}{\sigma(x)} + b_i \]

Latent Space Interpolation⚓︎

潜在空间是平滑的(smooth)
给定潜在向量 $z_0, z_1$，我们能在两者之间做插值：

\[ \begin{aligned} z_t & = tz_0 + (1 - t)z_1 \\ x_t & = G(z_t) \end{aligned} \]
结果图像 $x_t$ 可以在样本之间平滑插值

效果

Karras et al, ”Alias-Free Generative Adversarial Networks”, NeurIPS 2021

总结

GAN 在大约 2016-2021 年是首选的模型。

优点：
- 形式化简单
- 非常好的图像质量
缺点：
- 无法查看损失曲线
- 训练不稳定
- 很难扩展到大模型 + 数据

Diffusion Models⚓︎

警告

该领域的术语和符号没有统一：存在许多不同的数学表达；不同论文的术语和符号存在大量差异。所以下面只介绍现代的“干净”实现（即校正流）的基础知识。

扩散模型(diffusion models) 的大致思路如下：

选取一个噪声分布(noise distribution) $z \sim p_{\text{noise}}$（通常使用单位高斯分布）
数据 $x$ 被不同噪声等级(noise levels) $t$ 破坏后得到的噪声数据 $x_t$
训练一个神经网络 $f_\theta(x_t, t)$，以移除一些噪声
在推理期间，从 $x_1 \sim p_{\text{noise}}$ 采样并且连续多次应用 $f_\theta$，以生成无噪声的样例 $x_\theta$

Rectified Flow⚓︎

校正流(rectified flow) 的思路：

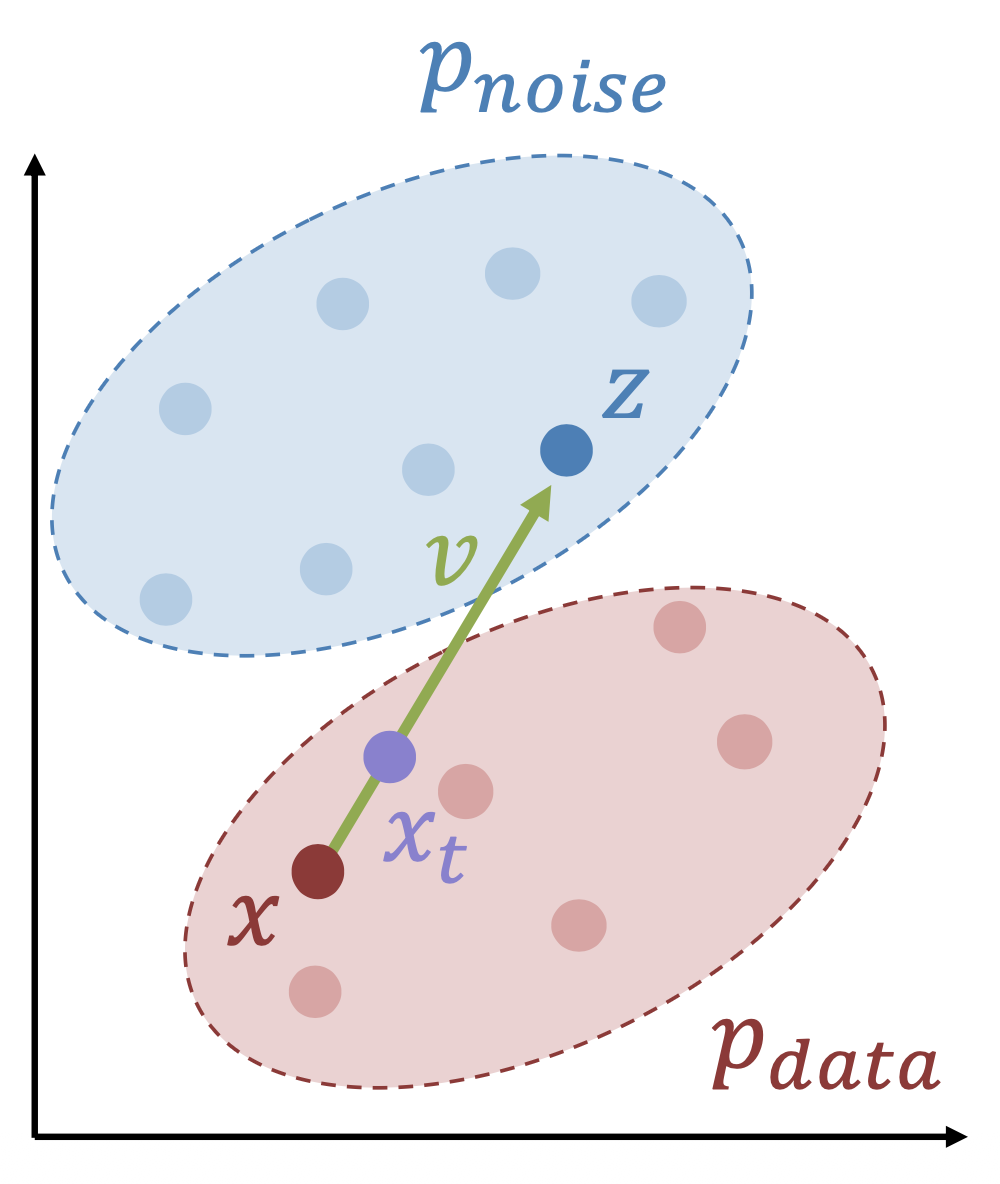
假设有来自 $\textcolor{red}{p_{\text{data}}}$ 的一个简单噪声 $\textcolor{cornflowerblue}{p_{\text{noise}}}$（比如高斯分布）和样本
在每一次训练迭代中，在以下分布中采样：

\[ \textcolor{cornflowerblue}{z} \sim \textcolor{cornflowerblue}{p_{\text{noise}}} \quad \textcolor{red}{x} \sim \textcolor{red}{p_{\text{data}}} \quad t \sim \text{Uniform}[0, 1] \]
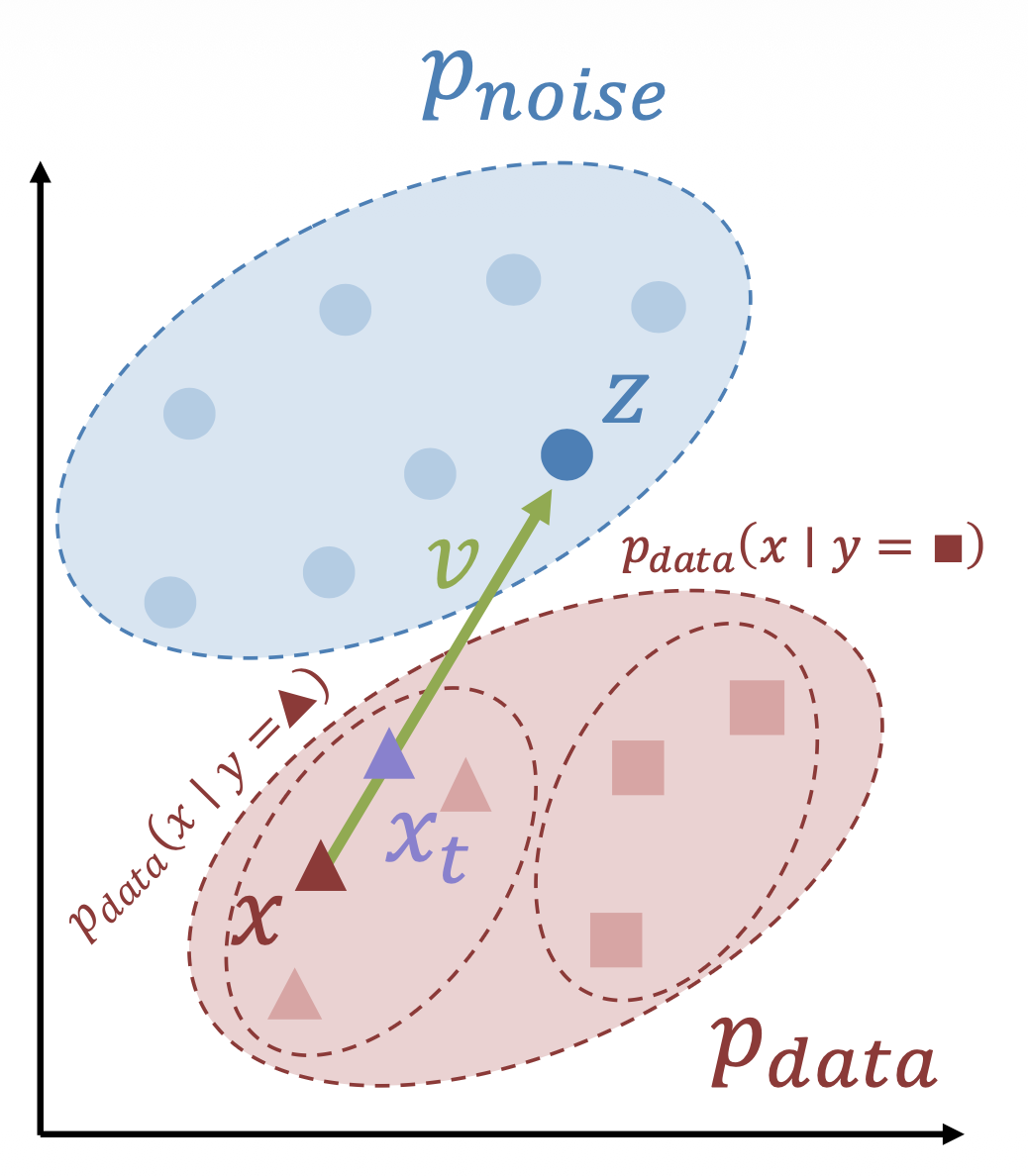
设置 $\textcolor{plum}{x_t} = (1 - t)\textcolor{red}{x} + tz, \textcolor{yellowgreen}{v} = \textcolor{cornflowerblue}{z} - \textcolor{red}{x}$
训练一个预测 $v$ 的神经网络：

\[ L = \|f_\theta(\textcolor{plum}{x_t}, t) - \textcolor{yellowgreen}{v}\|_2^2 \]

核心的训练循环仅需几行代码：

for x in dataset:
    z = torch.randn_like(x)
    t = random.uniform(0, 1)
    xt = (1 - t) * x + t * z
    v = model(xt, t)
    loss = (z - x - v).square().sum()

采样阶段：
- 选择迭代次数 $T$（通常 $T = 50$）
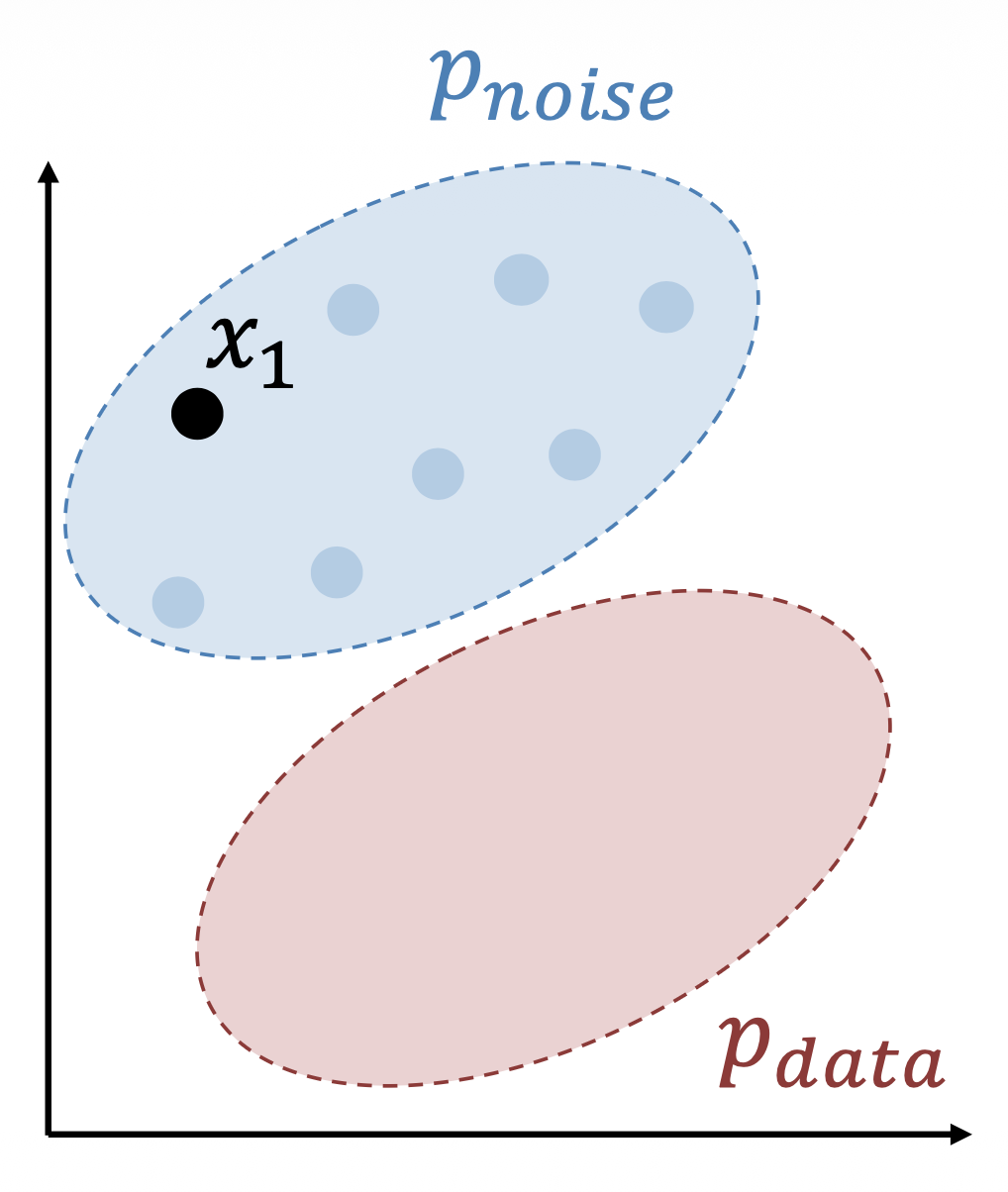
- 从 $\textcolor{cornflowerblue}{x} \sim \textcolor{cornflowerblue}{p_{\text{noise}}}$ 采样
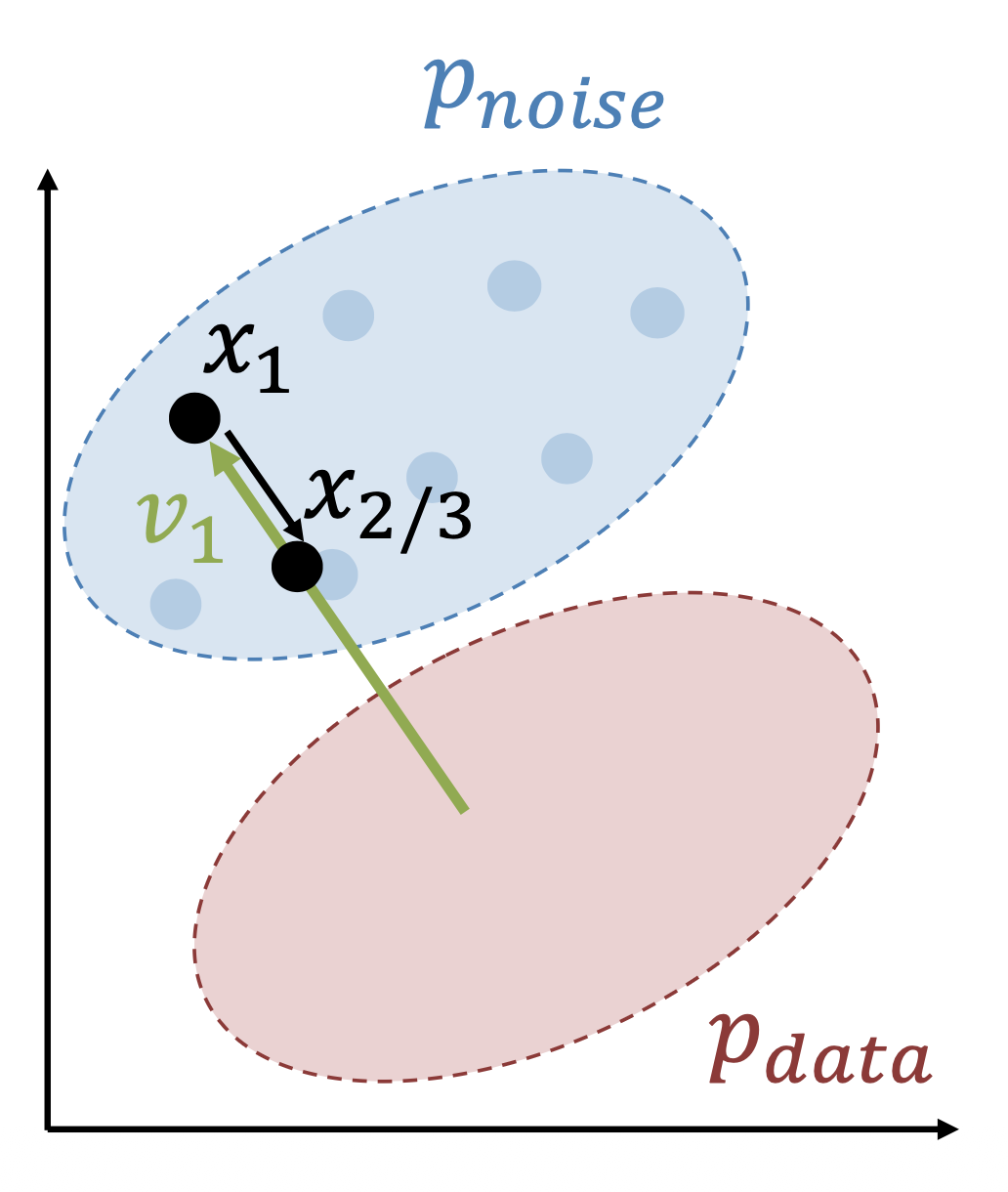
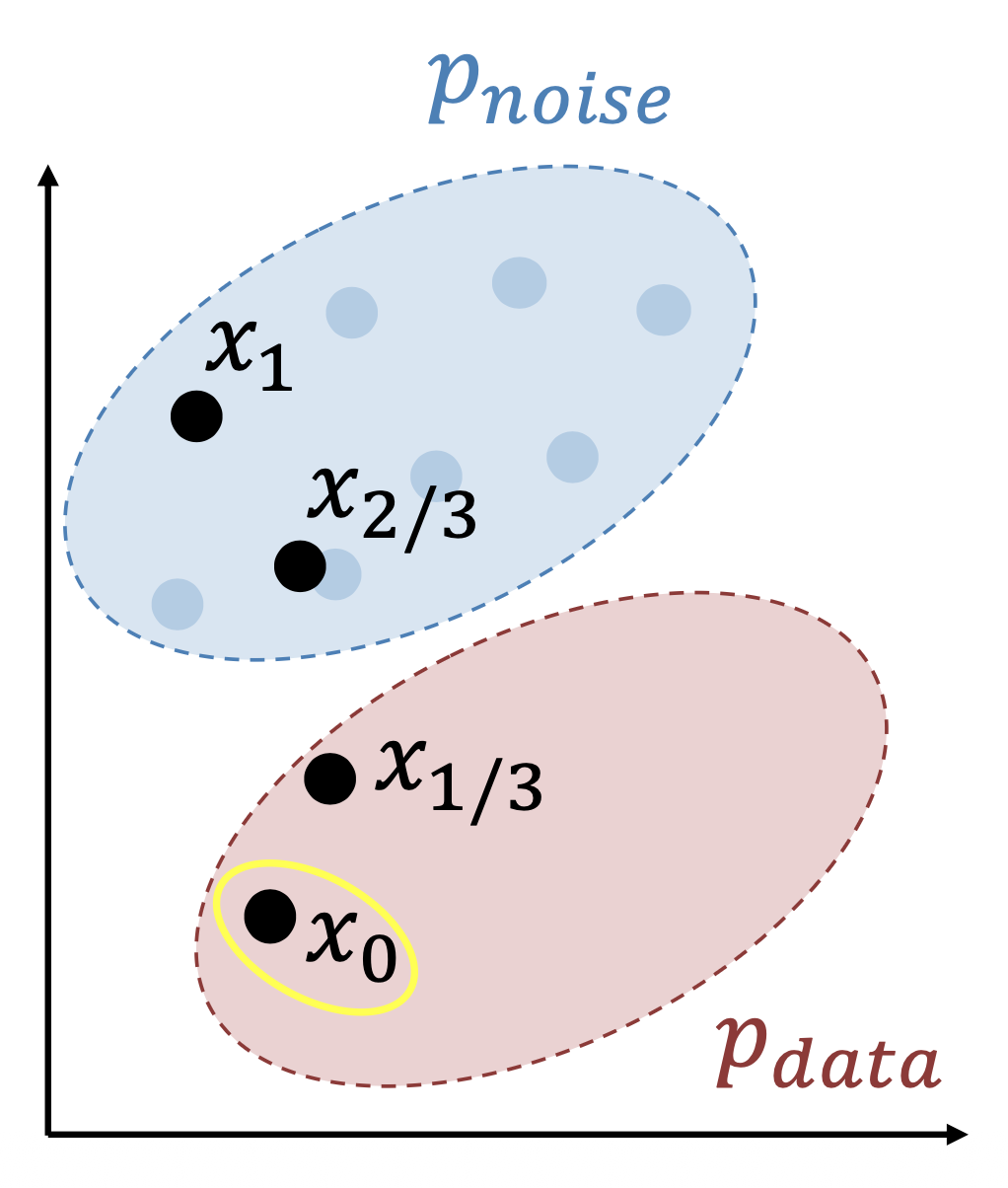
- 对于在 $[1, 1 - \dfrac{1}{T}, 1 - \dfrac{2}{T}], \dots, 0$ 内的 $t$
  - 求解 $\textcolor{yellowgreen}{v_t} = f_\theta(x_t, t)$
  - $x = x - \dfrac{v_t}{T}$
- 返回 $x$
- 对应代码为：
```
sample = torch.randn(x_shape)
for t in torch.linspace(1, 0, num_steps):
    v = model(sample, t)
    sample = sample - v / num_steps
```

Conditional Rectified Flow⚓︎

条件校正流在原版基础上有了以下修改：

训练：

for (x, y) in dataset:
    z = torch.randn_like(x)
    t = random.uniform(0, 1)
    xt = (1 - t) * x + t * z
    v = model(xt, y, t)
    loss = (z - x - v).square().sum()

采样：

y = user_input()
sample = torch.randn(x_shape)
for t in torch.linspace(1, 0, num_steps):
    v = model(sample, y, t)
    sample = sample - v / num_steps

Classifier-Free Guidance (CFG)⚓︎

无分类器指导(classifier-free guidance, CFG) 是在条件校准流的基础上实现对条件 $y$ 强调程度的控制。

训练：
```
for (x, y) in dataset:
    z = torch.randn_like(x)
    t = random.uniform(0, 1)
    xt = (1 - t) * x + t * z
    if random.random() < 0.5: y = y_null
    v = model(xt, y, t)
    loss = (z - x - v).square().sum()
```
- 在训练过程中随机删除 $y$，此时模型可同时是条件的和无条件的
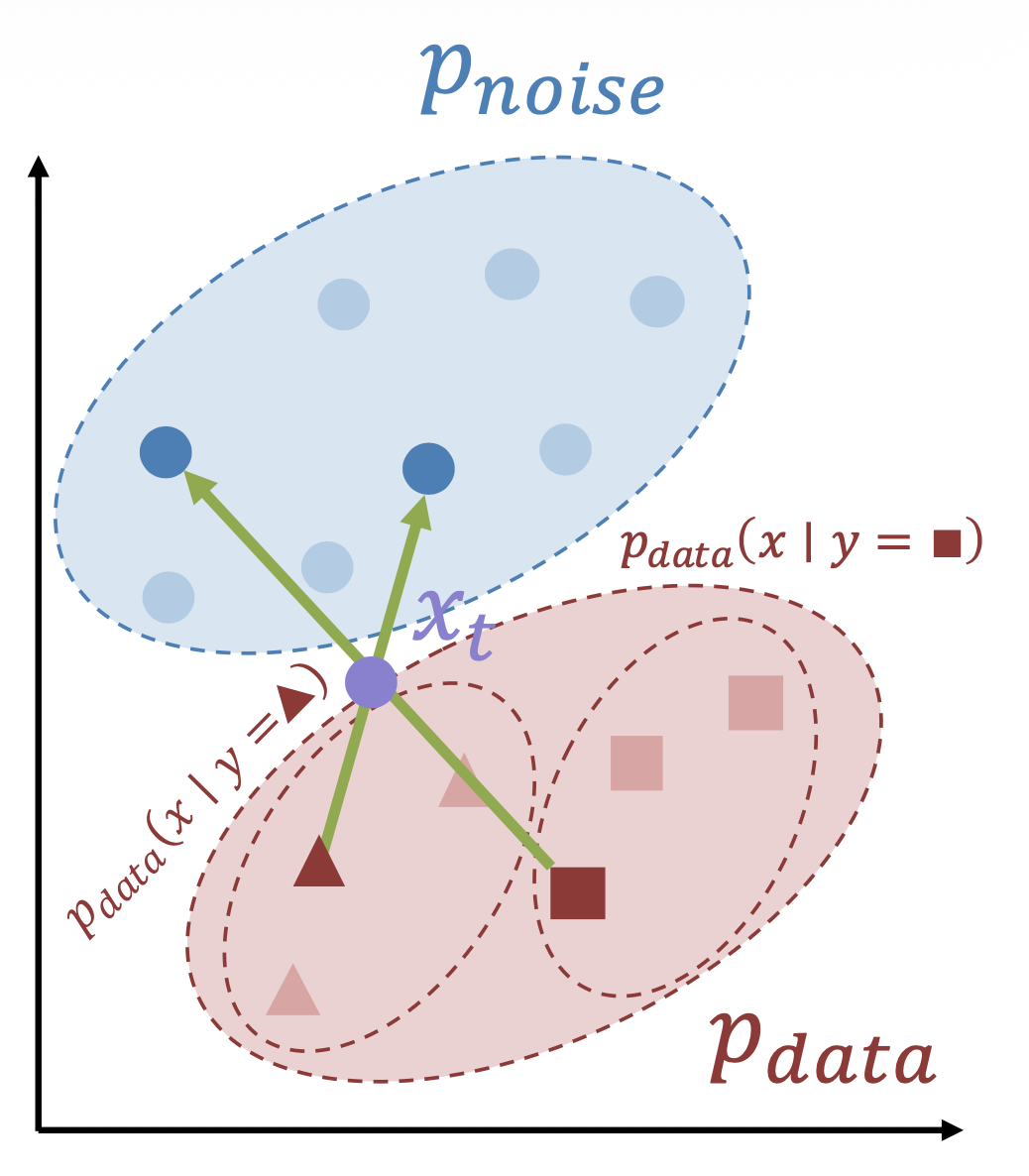
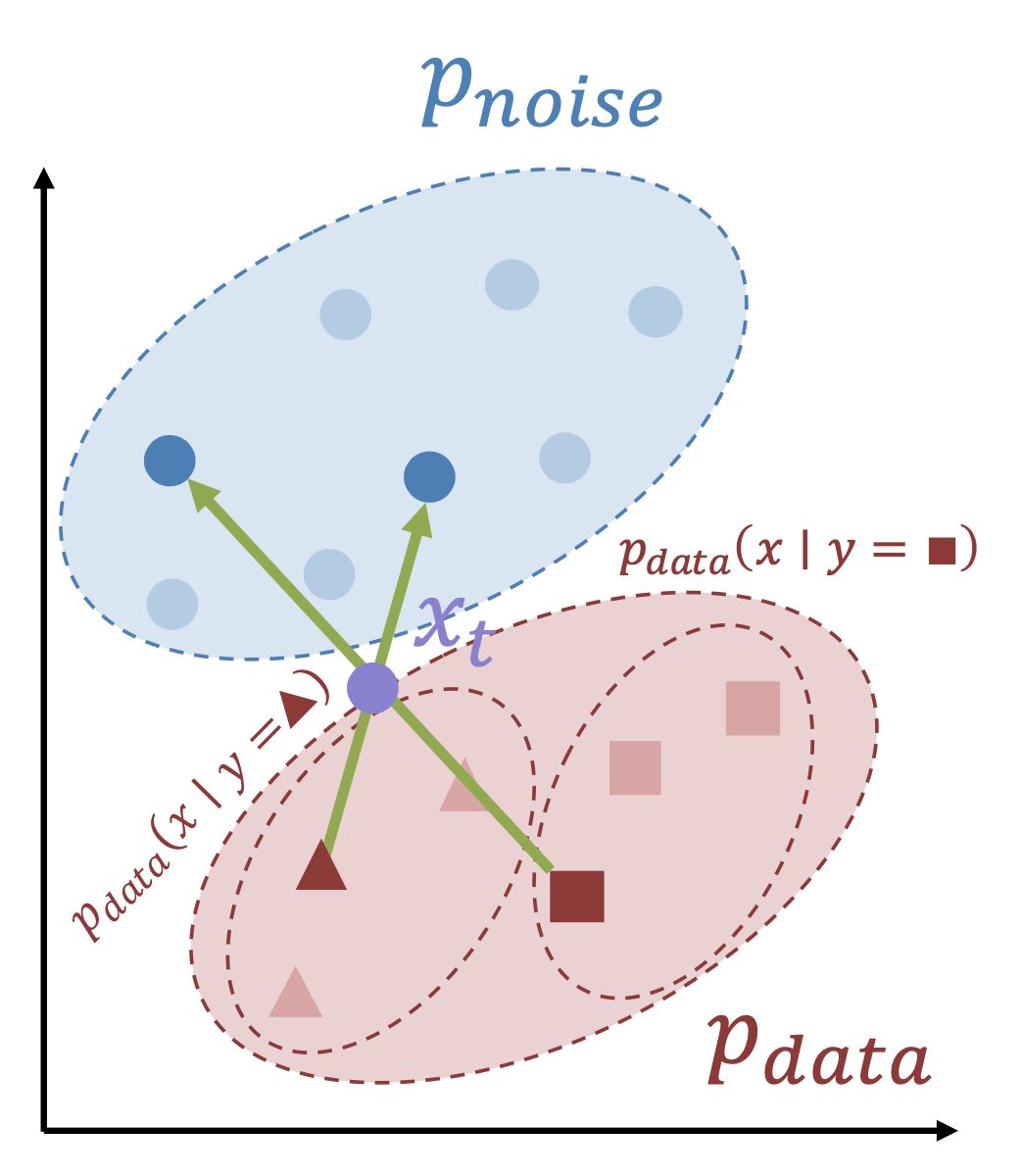
- 如右图所示，考虑噪声 $\textcolor{plum}{x_t}$：
  - $\textcolor{orange}{v^{\emptyset} = f_\theta (x_t, y_\emptyset, t)}$ 指向 $p(x)$
  - $\textcolor{yellowgreen}{v^y = f_\theta (x_t, y, t)}$ 指向 $p(x | y)$
  - $\textcolor{cornflowerblue}{v^{cfg}} = (1 + w)\textcolor{yellowgreen}{v^y} - w \textcolor{orange}{v^{\emptyset}}$ 更多指向 $p(x | y)$
  - 在采样过程中，根据 $\textcolor{cornflowerblue}{v^{cfg}}$ 步进

采样：

y = user_input()
sample = torch.randn(x_shape)
for t in torch.linspace(1, 0, num_steps):
    vy = model(sample, y, t)
    v0 = model(sample, y_null, t)
    v = (1 + w) * vy - w * v0
    sample = sample - v / num_steps

实际上到处使用，对于高质量的输出而言非常重要
问题：采样成本加倍

之所以叫做 "classifier-free"，是因为先前的方法使用单独的判别模型 $p(y|x)$ 来计算步进方向 $\dfrac{\partial}{\partial x} \log p(y|x)$ 的。

Optimal Prediction (Noise Schedules)⚓︎

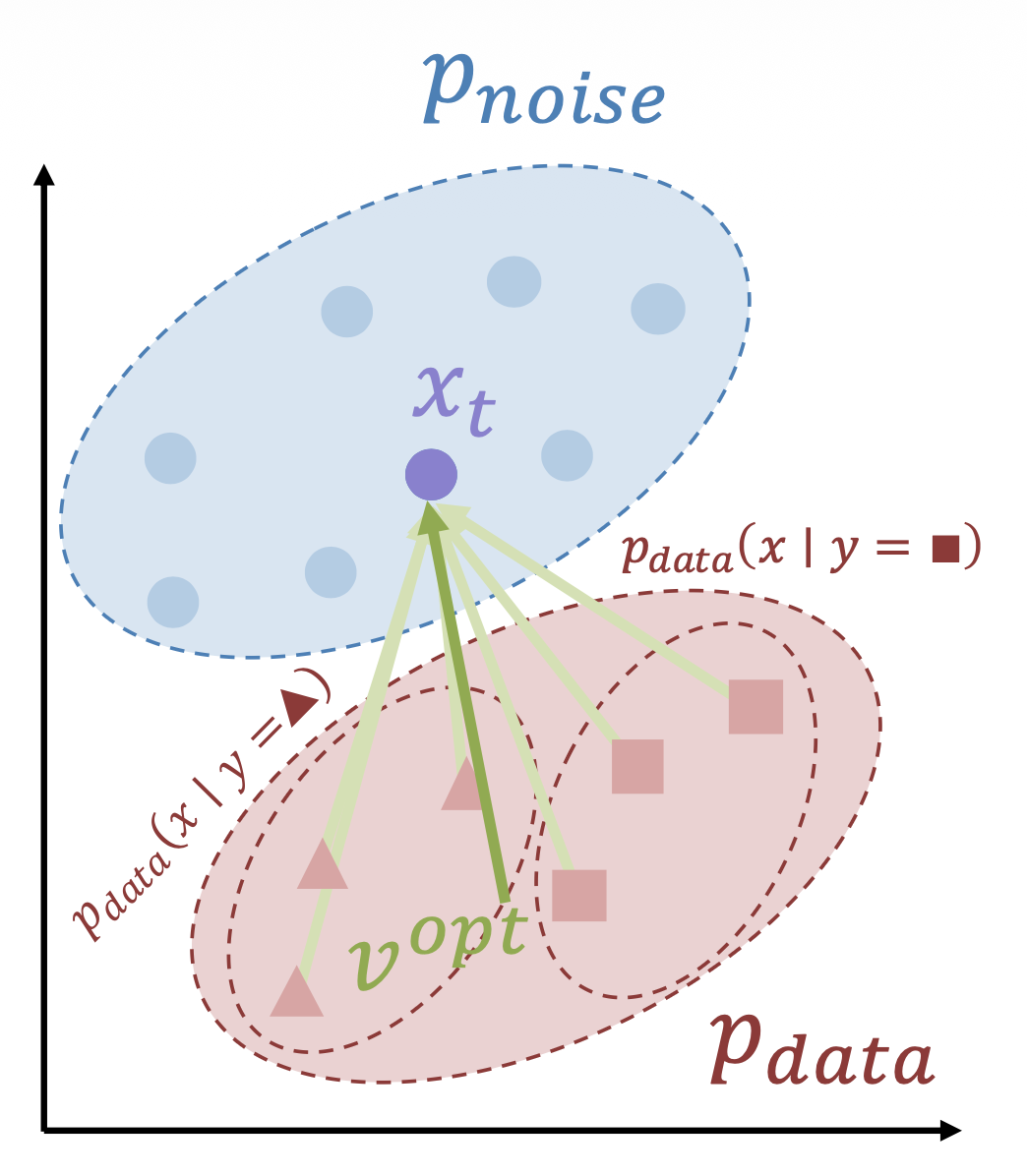
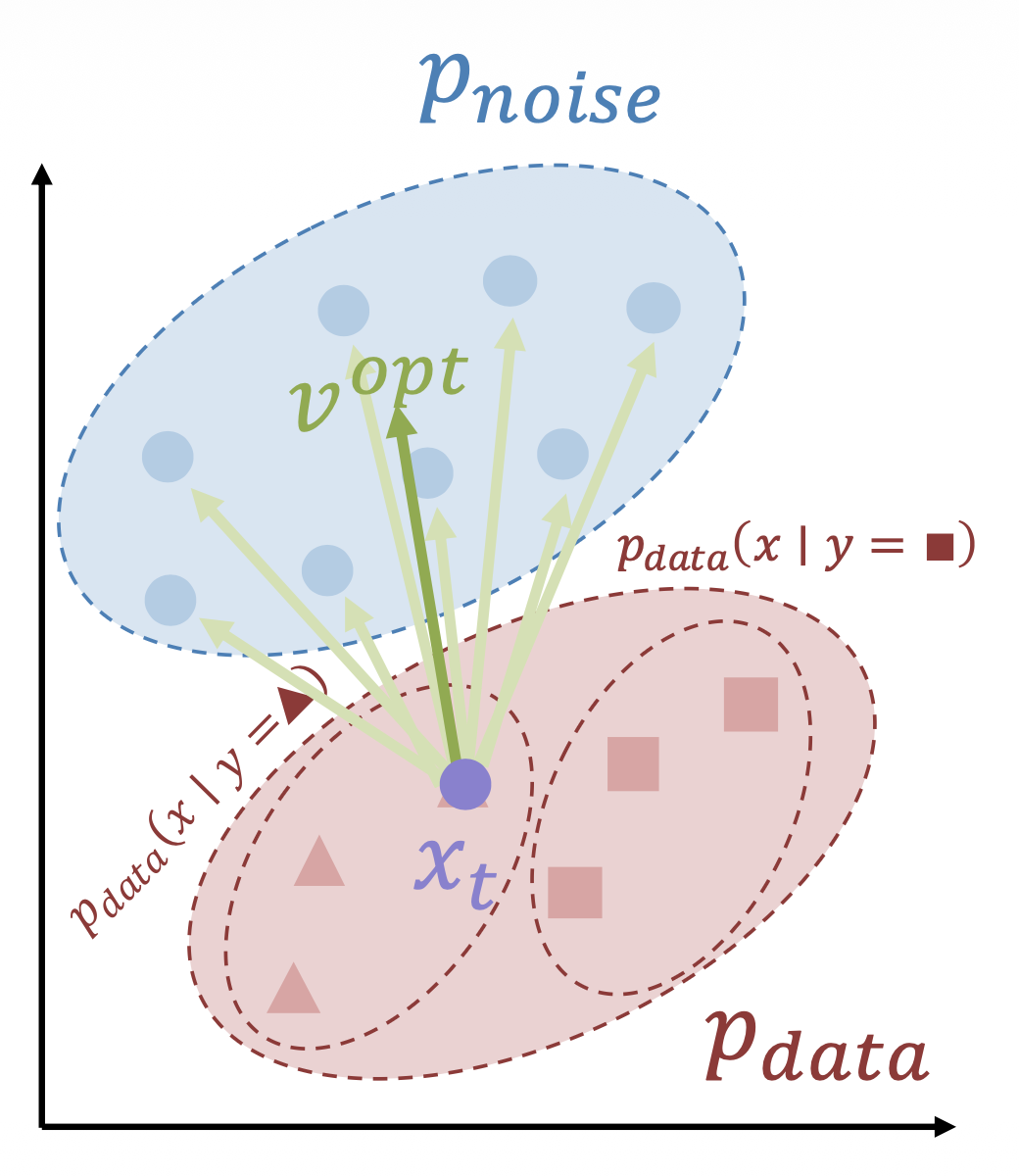
上述方法中，存在多个 $(x, z)$ 对给出相同的 $x_t$，网络必须计算它们的平均值

完全噪声（$t=1$）很容易：最优的 $v$ 是 $p_\text{data}$ 的均值
没有噪声（$t=1$）也很容易：最优的 $v$ 是 $p_\text{noise}$ 的均值
中间的噪声是最困难也是最模糊的，但问题是我们为所有的噪声等级赋予了相同的权重

解决方法：使用非均匀噪声调度(noise schedule)。

在中间多放置一些噪声
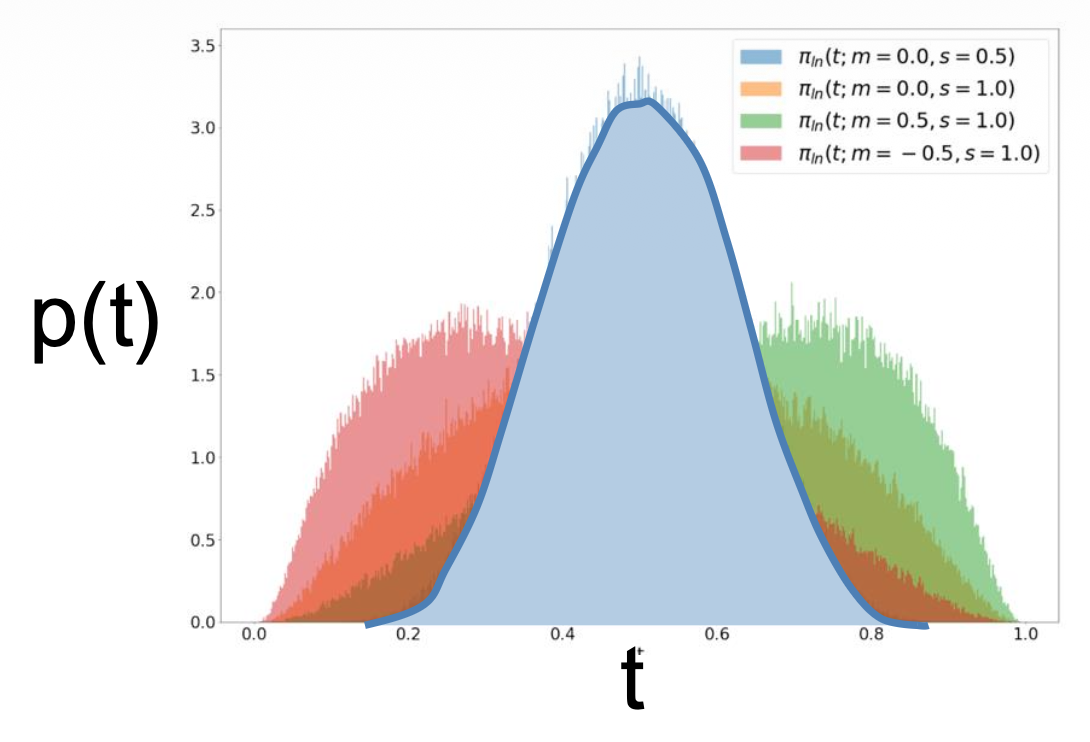
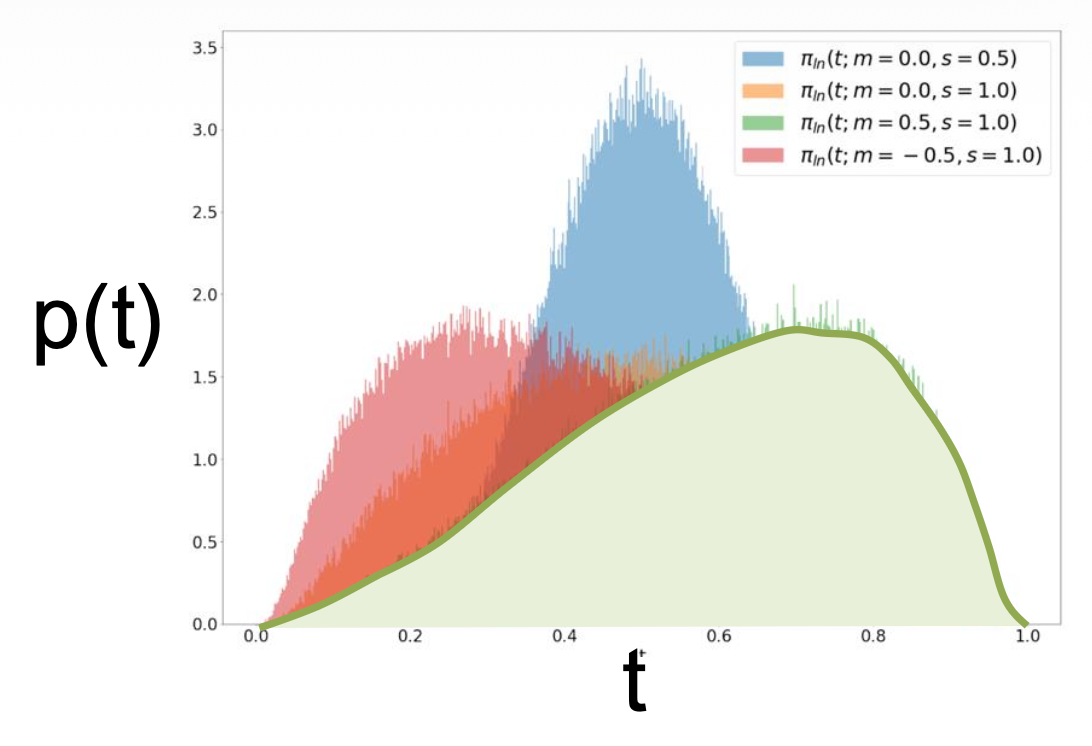
常用方法：对数正态采样(logit normal sampling)
对于高分辨率区域，考虑像素相关性，通常转向更高的噪声

对应代码如下：

for (x, y) in dataset:
    z = torch.randn_like(x)
    t = torch.randn(()).sigmoid()
    xt = (1 - t) * x + t * z
    if random.random() < 0.5: y = y_null
    v = model(xt, y, t)
    loss = (z - x - v).square().sum()

优点：对于多数生成式建模问题而言是简单且可扩展的设置
缺点：无法在高分辨率数据上简单工作

Latent Diffusion Models (LDMs)⚓︎

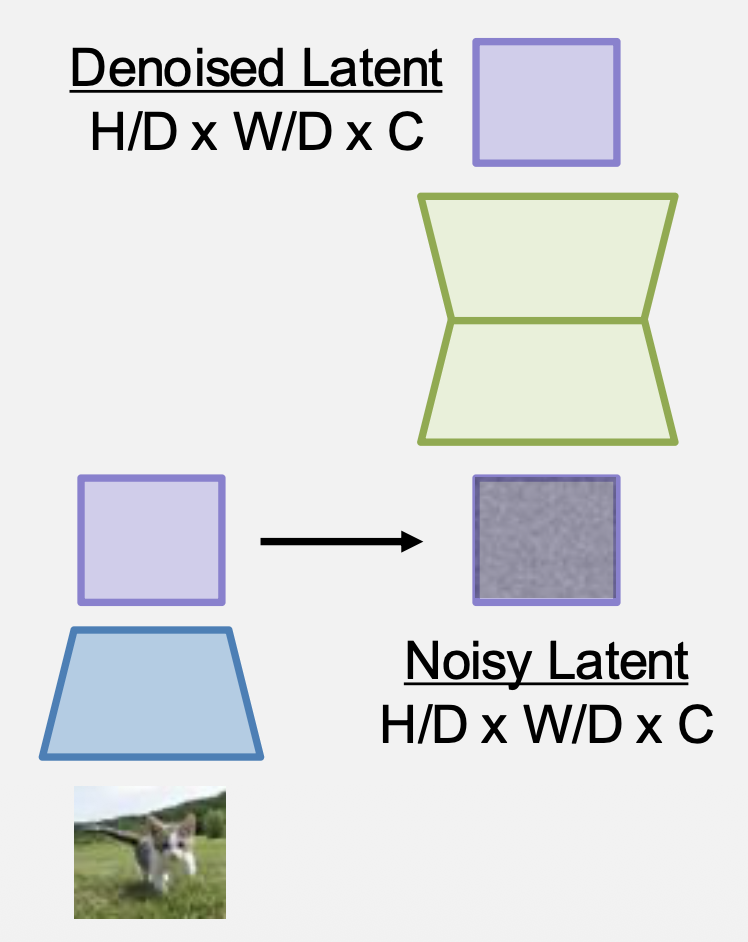
潜扩散模型(latent diffusion models, LDMs) 的思路为：

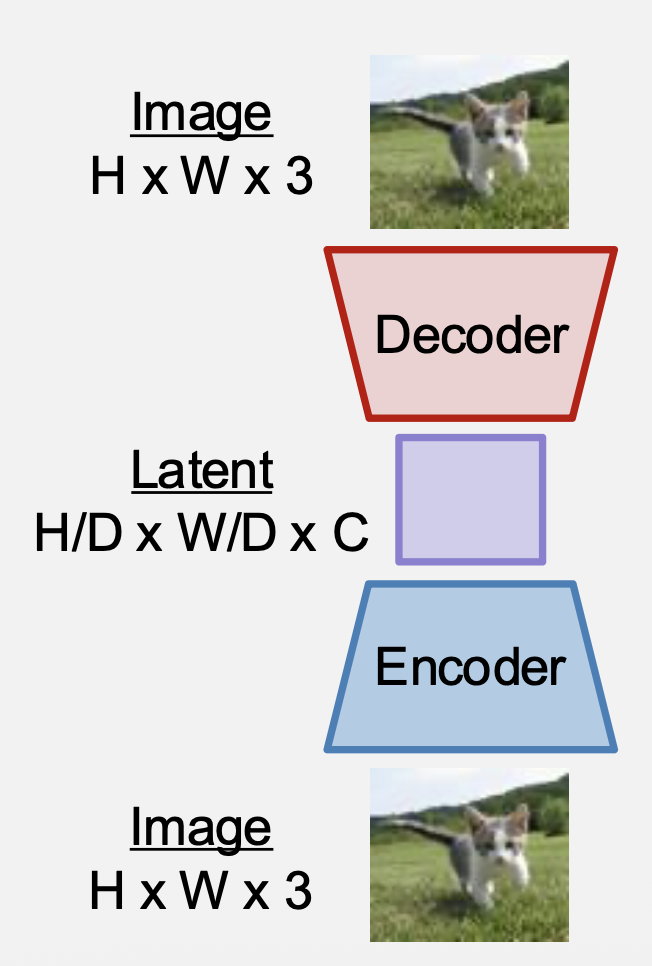
训练编码器 + 解码器，将图像转换为潜变量(latent)
- 常用设置：D=8, C=16
- 图像（256x256x3）=> 潜变量（32x32x16）
- 编码器和解码器是带注意力的 CNNs
训练扩散模型，以移除潜变量的噪声（编码器被固定住）
训练后：
- 采样随机潜变量
- 迭代应用训练模型以移除噪声
- 运行解码器以获得图像

潜扩散是目前最常用的形式。

不难发现，这种架构也是一种 VAE，而且带有很小的 KL 先验权重。所以就按 VAE 的训练方式来训练编码器和解码器。

但有一个问题：解码器的输出不确定 (blurry)。解决方案是加一个判别器，形成类似 GAN 的架构。

综上，现代的 LDM 流水线是 VAE + GAN + 扩散的结合。

Diffusion Transformer (DiT)⚓︎

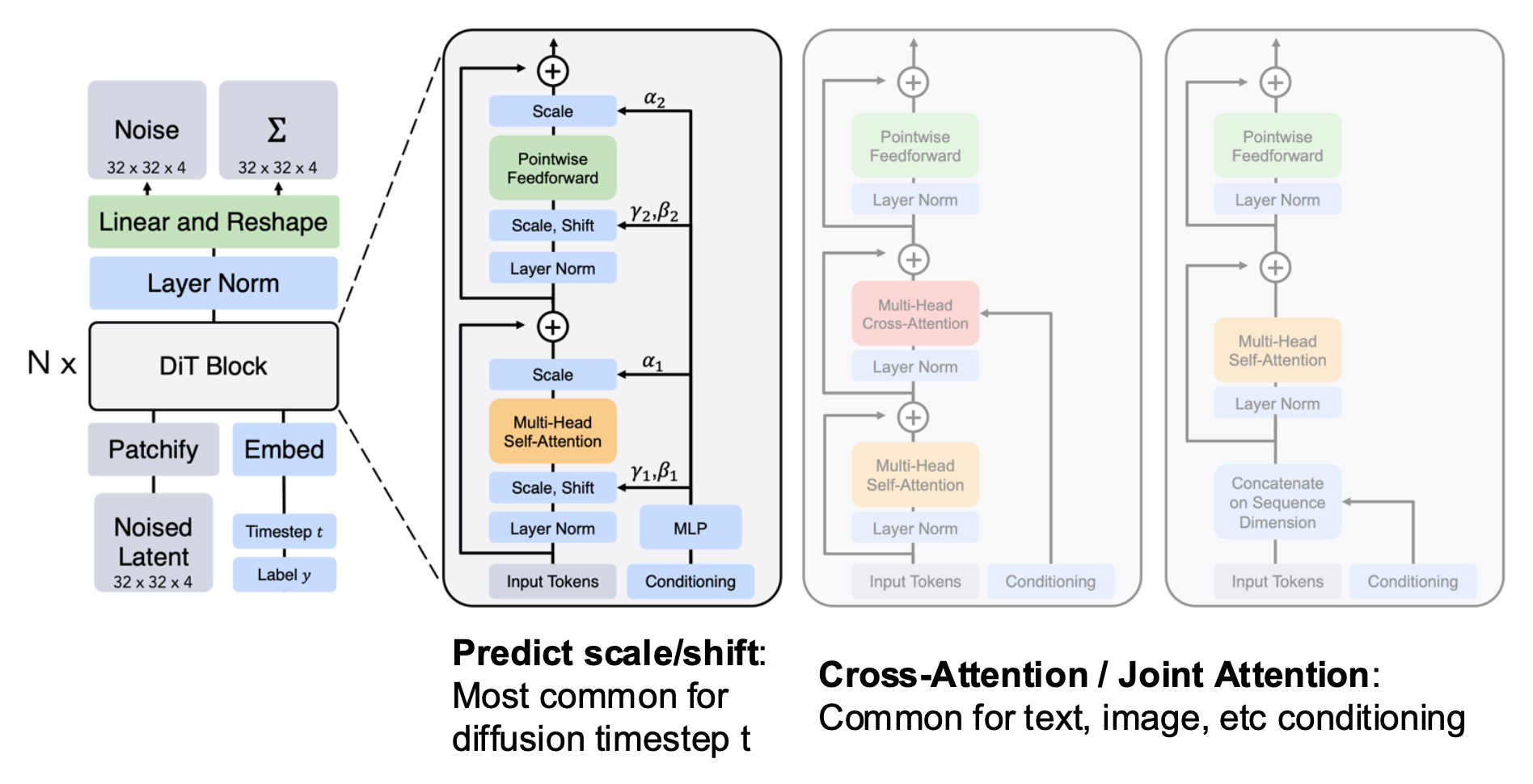
扩散模型采用标准的 Transformer 块。

主要问题：如何注入条件（时间步 t，文本 ...）：

预测尺度 / 偏移：常用于扩散时间步 t
交叉注意 / 联合注意：常用于文本、图像等条件

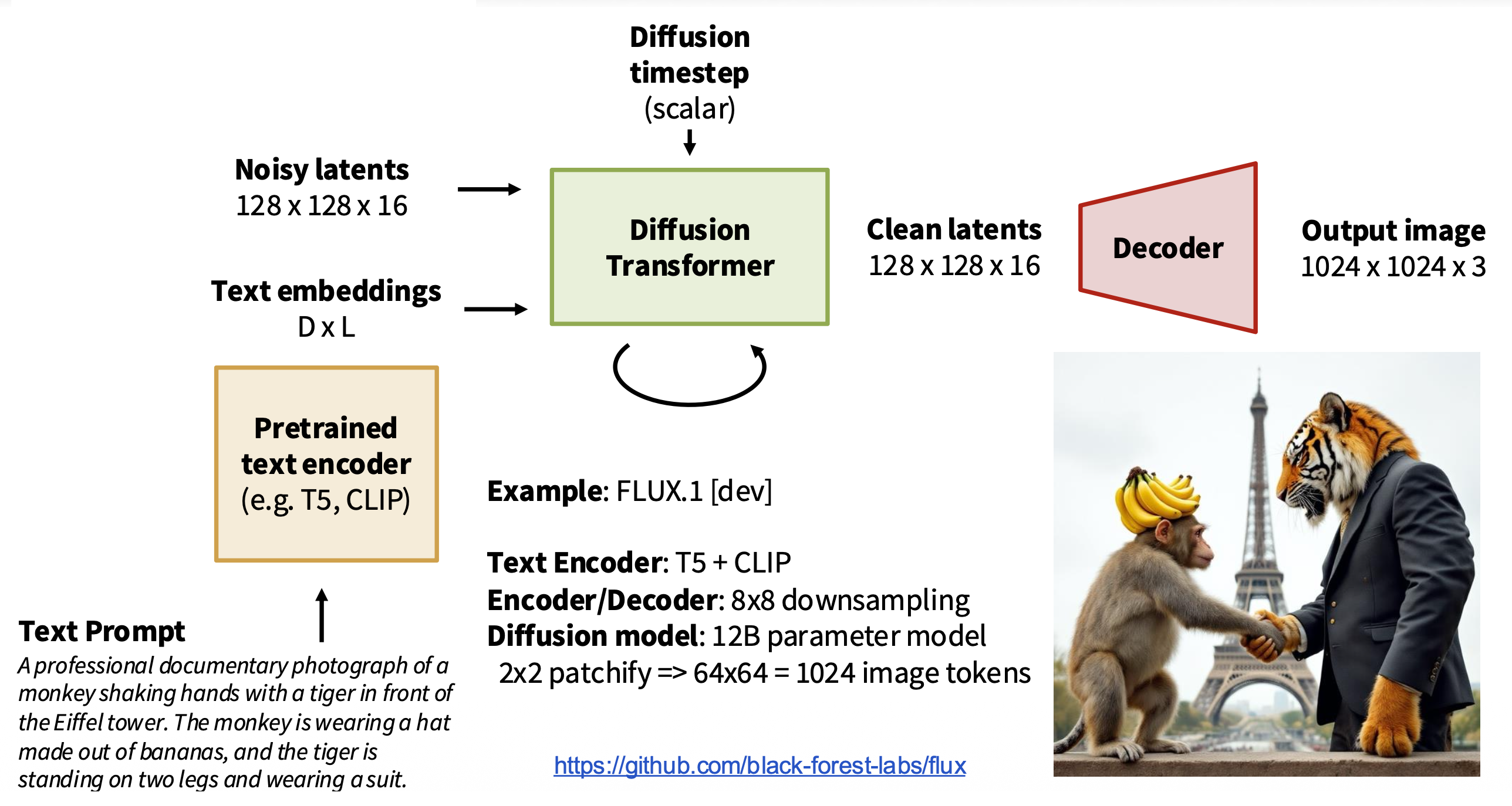
Text-to-Image⚓︎

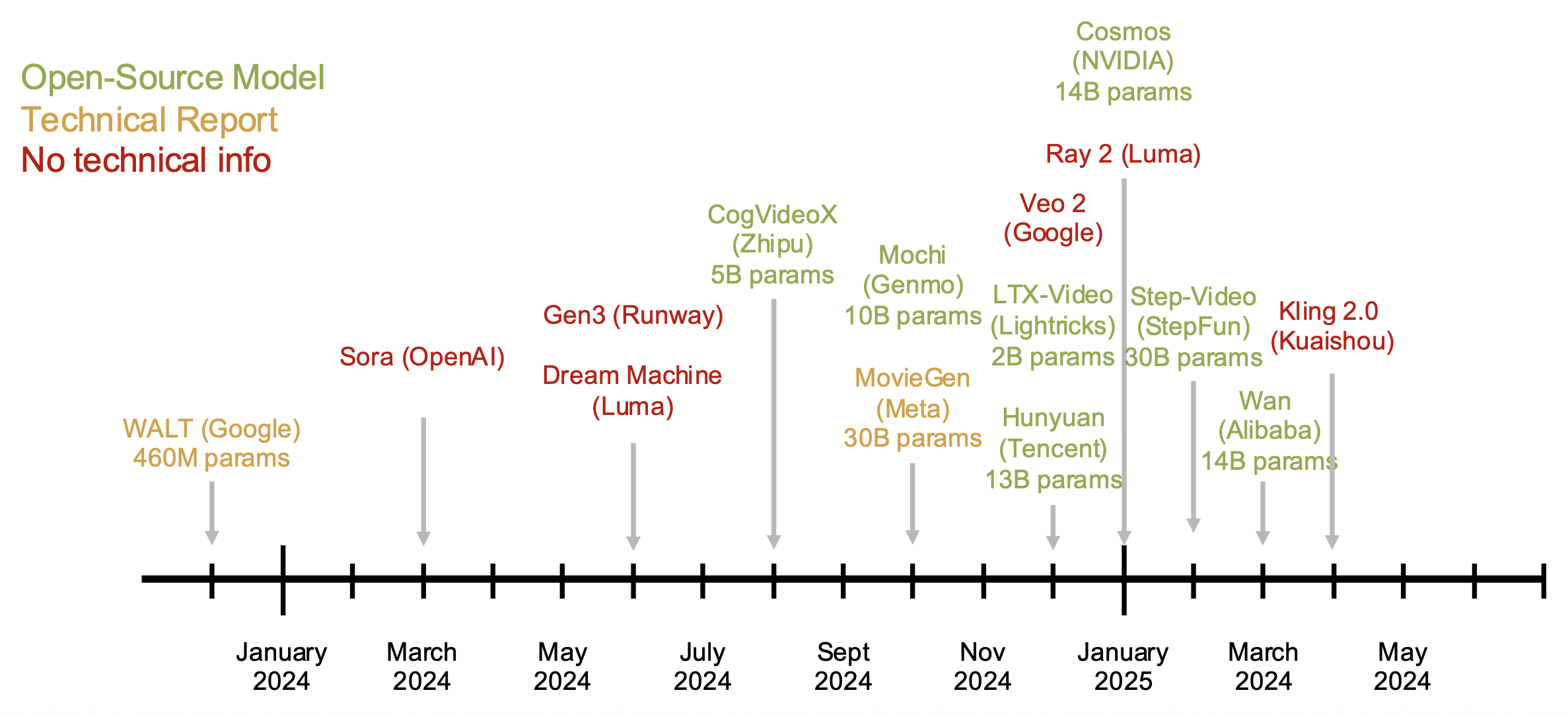
Text-to-Video⚓︎

视频扩散模型的时代：

Diffusion Distillation⚓︎

问题

在采样过程中，我们需要多次运行扩散模型（在校正流中大约是 30-50 次）。显然速度非常慢。

解决方案：使用蒸馏算法(distillation algorithms)，减少步数。该方法也可在 CFG（无分类器指导）中烘培。

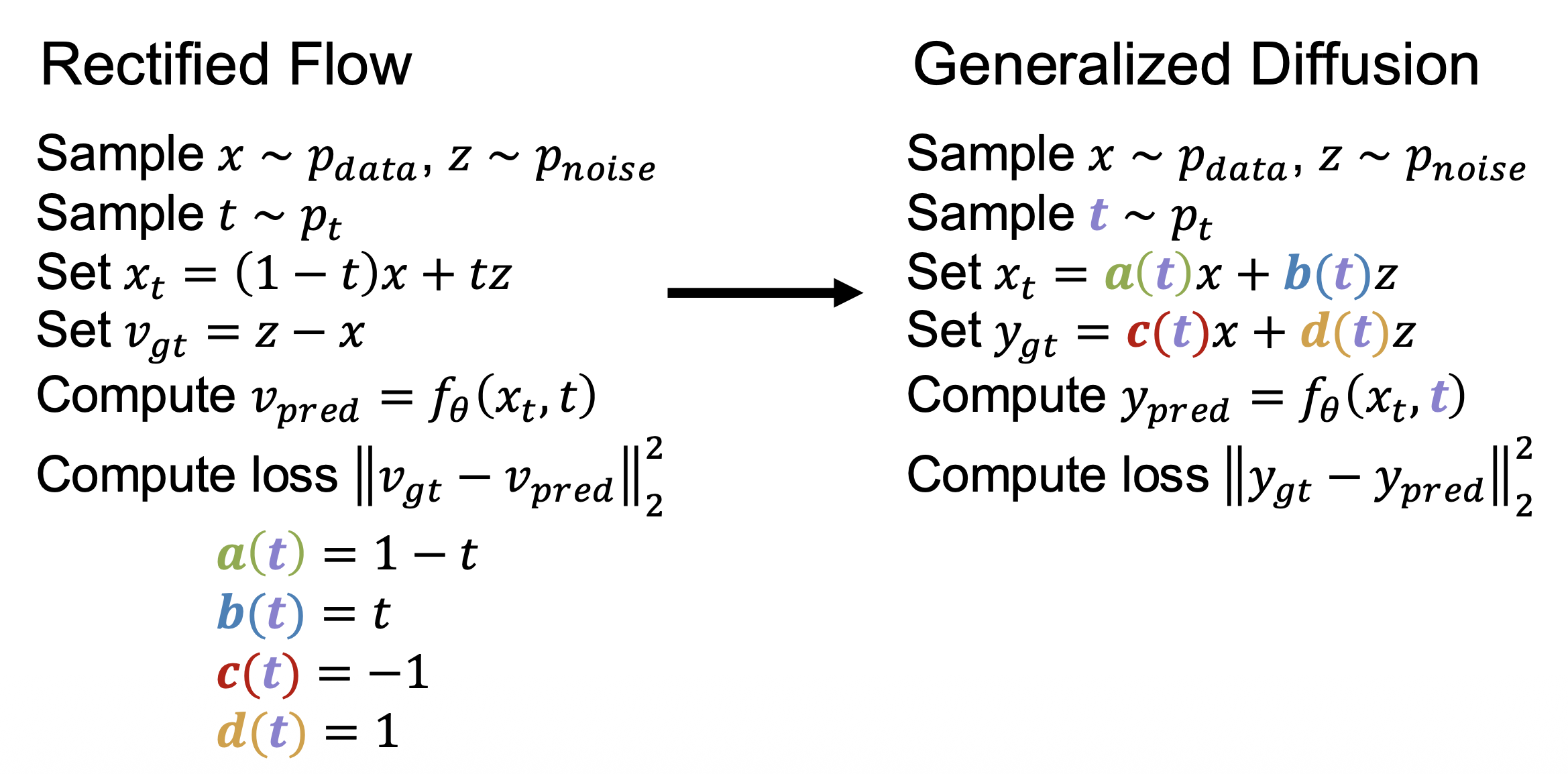
Generalized Diffusion⚓︎

广义扩散(generalized diffusion) 模型的数学公式如下图右侧所示（和校正流对应）：

各种变体：

方差保留(variance preserving, VP)：
- $a(t) = \sqrt{\sigma(t)}$
- $b(t) = \sqrt{1 - \sigma(t)}$
- 若 $x, z$ 独立且方差为 1，那么 $x_t$ 的方差也为 1
方差爆炸(variance exploding, VE)：
- $a(t) = 1$
- $b(t) = \sqrt{\sigma(t)}$
- $\sigma(1)$ 需要足够大，以抽取在 $x$ 中的全部信号
$x$- 预测

\[ y_{gt} = x \quad [\textcolor{red}{c(}\textcolor{plum}{t}\textcolor{red}{)} = 1; \textcolor{orange}{d(}\textcolor{plum}{t}\textcolor{orange}{)} = 0] \]
$\varepsilon$- 预测

\[ y_{gt} = \bm{z} \quad [\textcolor{red}{c(}\textcolor{plum}{t}\textcolor{red}{)} = 1; \textcolor{orange}{d(}\textcolor{plum}{t}\textcolor{orange}{)} = 0] \]
$v$- 预测

\[ y_{gt} = \textcolor{cornflowerblue}{b(}\textcolor{plum}{t}\textcolor{cornflowerblue}{)} z - \textcolor{yellowgreen}{a(}\textcolor{plum}{t}\textcolor{yellowgreen}{)} x \quad [\textcolor{red}{c(}\textcolor{plum}{t}\textcolor{red}{)} = \textcolor{cornflowerblue}{b(}\textcolor{plum}{t}\textcolor{cornflowerblue}{)}; \textcolor{orange}{d(}\textcolor{plum}{t}\textcolor{orange}{)} = -\textcolor{yellowgreen}{a(}\textcolor{plum}{t}\textcolor{yellowgreen}{)}] \]

通常通过一些数学形式主义 (mathematical formalism) 来选择上述函数。

Miscellaneous⚓︎

扩散是一个潜变量模型
- 前向过程：增加高斯噪声
- 学习一个用于近似后向过程的网络
- 优化变分下界（和 VAE 一样）
扩散习得一个分数函数
- 对于任意在 $x \in \mathbb{R}^N$ 上的分布 $p(x)$，分数函数
  
  \[ s: \mathbb{R}^N \rightarrow \mathbb{R}^N \quad s(x) = \dfrac{\partial}{\partial x} \log p(x) \]
  
  是一个指向高概率密度区域的向量场
- 扩散习得一个用于逼近关于 $p_\text{data}$ 的分数函数的神经网络
扩散能解出随机微分方程 (stochastic differential equations, SDE)
- 我们能以 SDE 形式描述一个连续的增加噪声过程
  
  \[ d\bm{x} = f(\bm{x}, t) dt + g(t) d\bm{w} \]
- 上式给出了数据 $x$、时间 $t$ 和噪声 $w$ 之间的无穷小 (infinitesimal) 变化关系
- 扩散习得一个用于近似求解该 SDE 的神经网络
扩散的不同视角：

截图来自 Sander Dieleman 的博客。

评论区

如果大家有什么问题或想法，欢迎在下方留言~