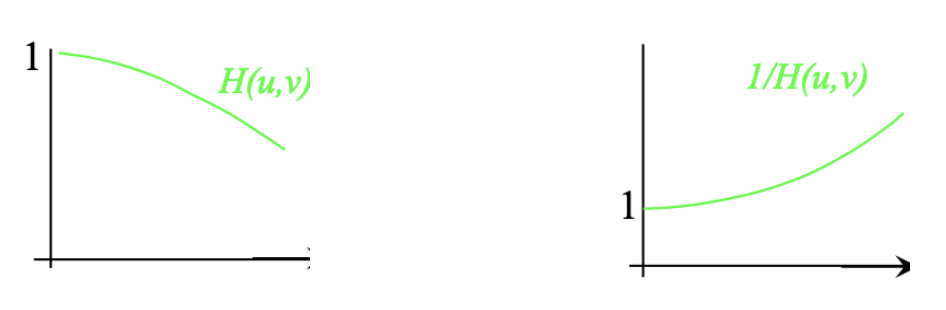Computational Photography⚓︎

计算摄影学(computational photography)

• 传感器记录的数据并非最终图像
• 对最终图像进行一定计算，从而达到我们想要的效果

High Dynamic Range Imaging (HDR)⚓︎

例子

曝光(exposure)：粗略地说，就是给定固定场景下捕获图像的“亮度 (brightness)”，可以用以下式子表示： $$ \text{Exposure} = \text{Gain} \times \text{Irradiance} \times \text{Time} $$

• 增益(gain) 由 ISO（感光度）控制

  
  • ISO 的副作用：随着 ISO 的增大，图像会变得非常粗糙，因为噪音被放大了

• 辐照度(irradiance) 由光圈(aperture) 控制

  

• 时间(time) 由快门速度(shutter speed) 控制

  

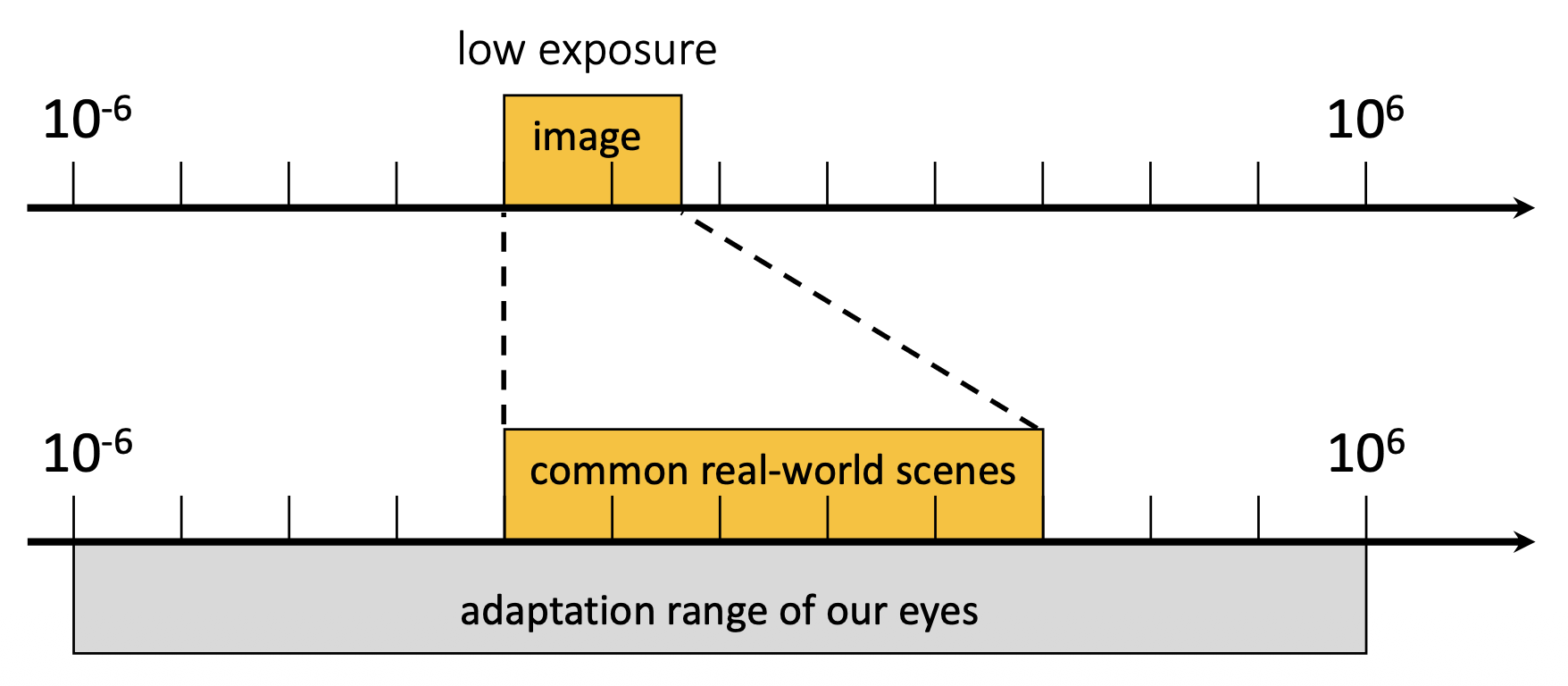
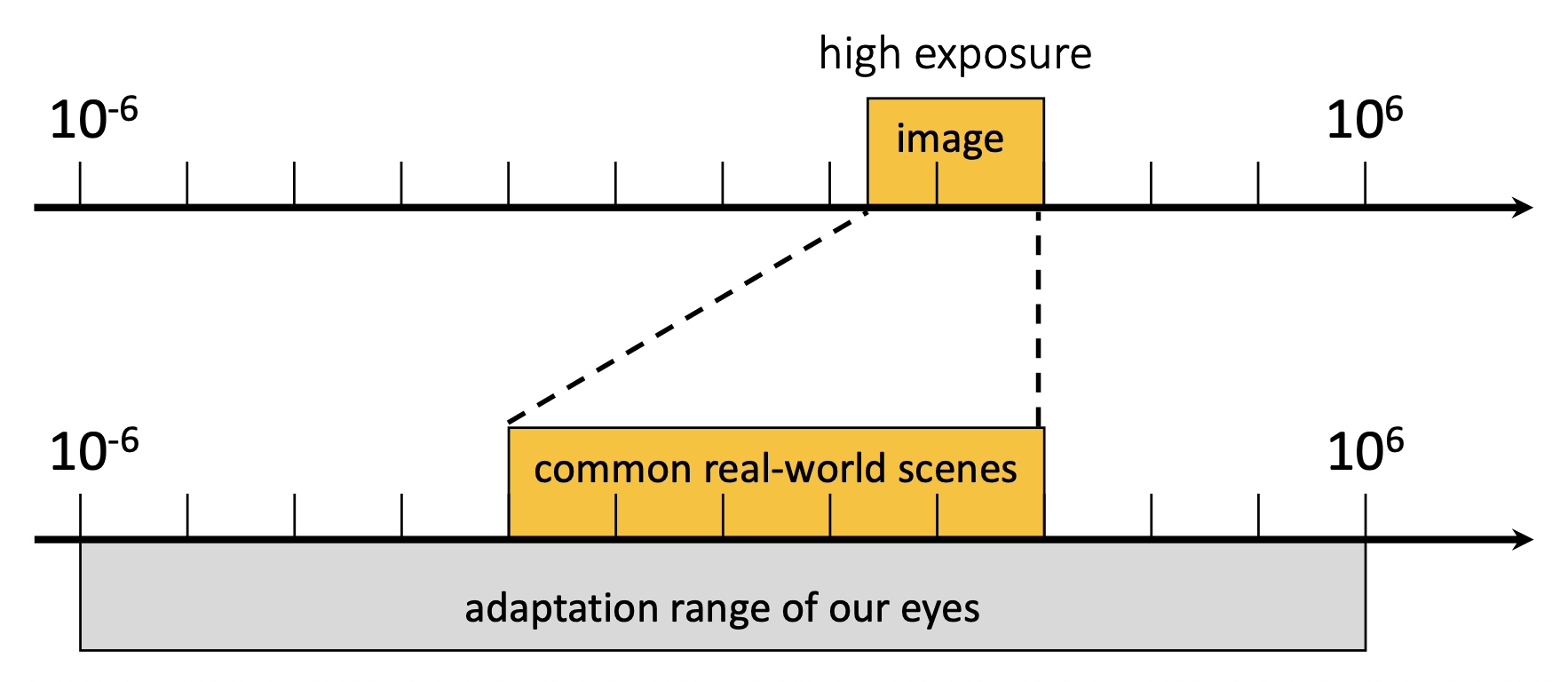
拍照时，平均曝光(averaged exposure) 应位于传感器测量范围的中间。这样照片既有亮部也有暗部，且细节丰富。

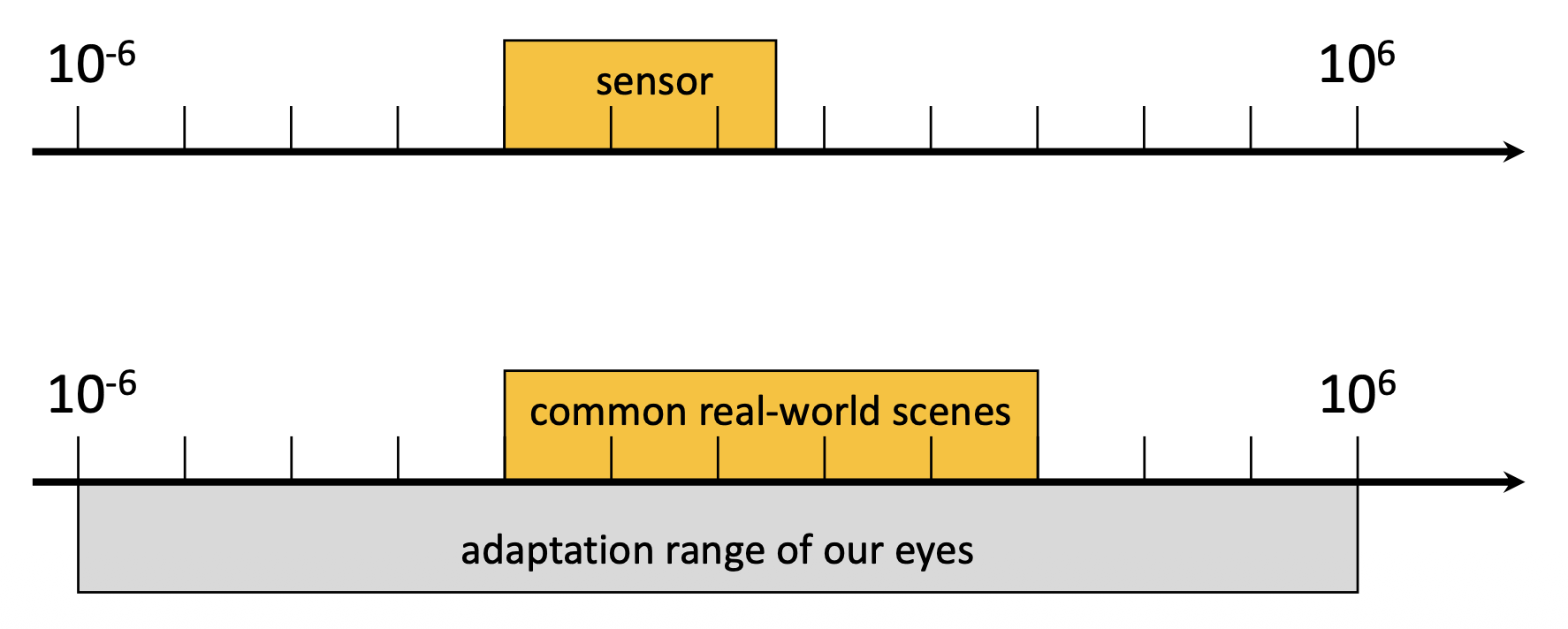
动态范围(dynamic range)：某一定量（通常是亮度）的最大值和最小值之间的比例。

比对

无 HDR 有 HDR

关键思路：

1. 曝光包围(exposure bracketing)：在不同曝光下捕捉多个 LDR 图像

   
   • 假设对于图像像素 \((x, y)\)，其场景辐射率 (radiance) 为 \(L(x, y)\)

   • 不同曝光时间下拍摄的图像：

     

   • 作为关于 \(L(x, y)\) 的函数，图像 \(I(x, y)\) 的表达式为：

     \[ I(x, y) = \text{clip}[t_i \cdot L(x, y) + \text{noise}] \]

     注：\(\text{clip}\) 函数限制像素值在合法范围内，比如超过最大值就强制设置为最大值

2. 合并(merging)：将它们合并成一张单张 HDR 图像

   

   • 对每个像素：

     1. 寻找每张图像上的“有效像素”（（噪声）0.05 < 像素 < 0.95（裁剪 (clipping)））

        

     2. 为有效像素值进行适当加权（像素值 / t _i）

     3. 形成一个新的像素值，作为有效像素值的加权平均

   • 合并结果：

     

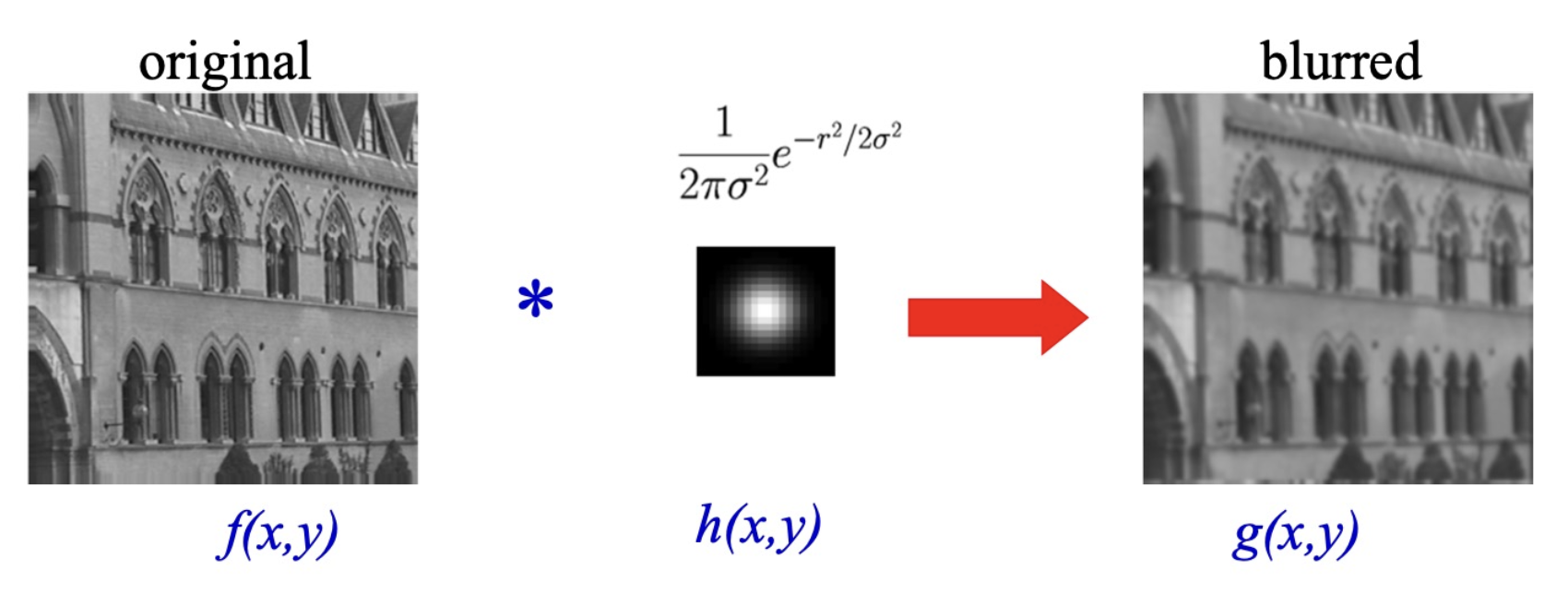
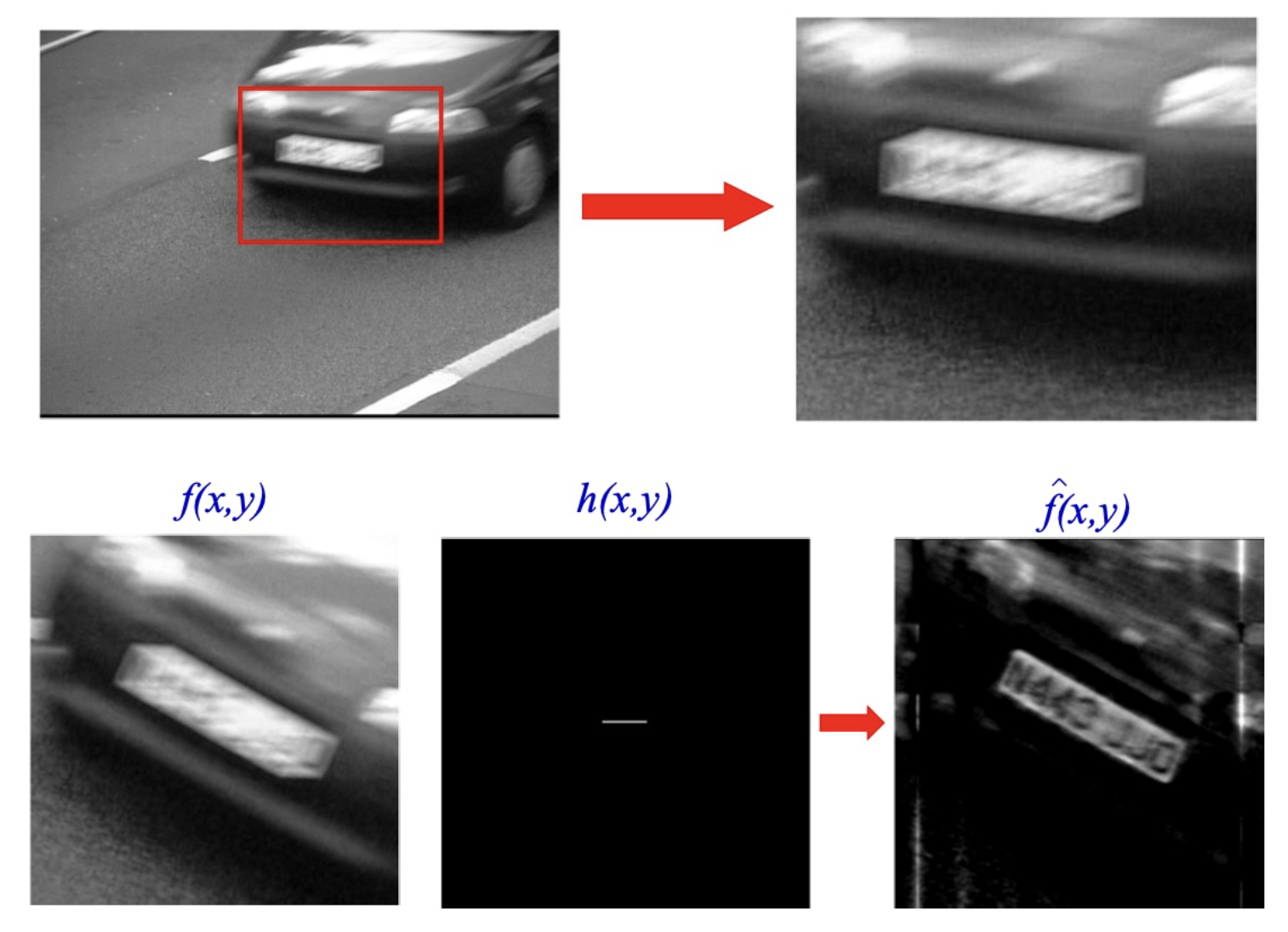
Deblurring⚓︎

图像模糊(blurring) 的原因：

• 失焦(defocus)：拍摄对象不在景深范围内

  

• 运动模糊(motion blur)：物体移动或相机不稳定

  

下面我们用数学建模来描述图像模糊：

• 模糊的过程可以通过卷积来描述
• 模糊后的图像称为卷积核(convolution kernel)

• 失焦模糊的模式取决于光圈形状
• 抖动(shaking) 模糊的模式取决于相机轨迹

例子

因此，去模糊(deblurring) 的操作等同于反卷积(deconvolution)。下面给出具体的实现方法：

Non-Blind Image Deconvolution (NBID)⚓︎

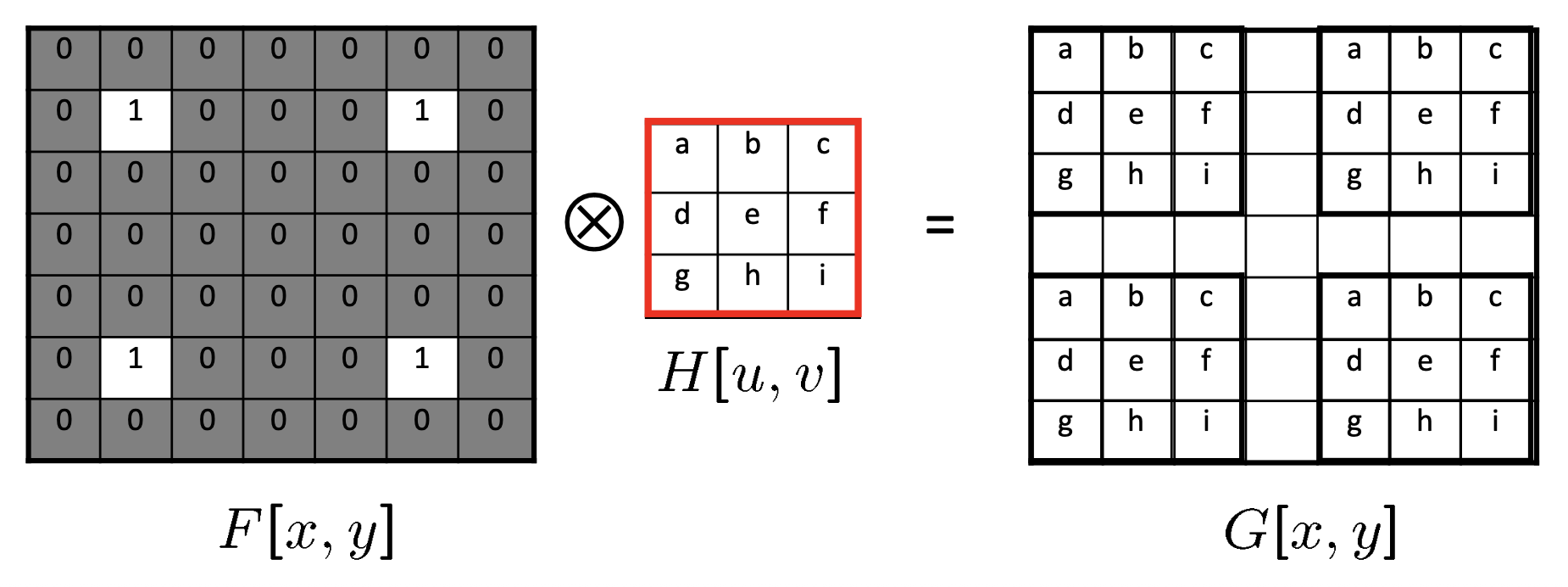
非盲图像反卷积(non-blind image deconvolution, NBID)

• \(G\)：捕获图像（已知）
• \(F\)：待求解图像（未知）
• \(H\)：卷积核（已知）

频域 (frequency domain) 反卷积：

• 空间域中的卷积 = 频率域中的乘积

  \[ FFT(G) = FFT(F \otimes H) = FFT(F) \times FFT(H) \]

• 那么，空间反卷积 = 频域中的除法

  \[ F = IFFT(FFT(G) \div FFT(H)) \]

• 通常称为逆滤波器(inverse filter)

  

例子

高斯模糊：

逆滤波的结果：

模糊核通常是一个低通滤波器，而逆滤波器会放大高频成分。

因此逆滤波器有可能会放大噪声：

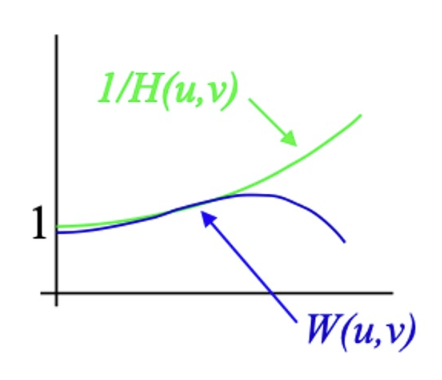
维纳滤波器(Wiener filter)：在逆滤波时抑制高频。

• 若 \(K = 0\)，那么 \(W(u, v) = 1 / H(u, v)\)，即逆滤波器
• 若 \(u, v\) 很大时，\(K \gg |H(u, v)|\)，那么高频将会衰减 (attenuated)
• \(K\) 是一个常量标量，根据经验设置

例子

应用

例 1 例 2：哈勃太空望远镜

Optimization⚓︎

还可以通过优化(optimization) 来实现反卷积。

• 优化的变量就是要被恢复的图像
• 目标函数
  • 模糊图像与给定模糊图像的相似度（可能性）
  • 恢复的图像看起来很真实（先验）

模糊图像生成过程： $$ G = F \otimes H + N $$

假设噪声 \(N\) 是高斯噪声，可能性可以通过均方误差（MSE）来衡量：

问题：反卷积是病态的(ill-posed)

换句话说就是存在多解：

可以看到，两个不同的解可以得到相同的 MSE。

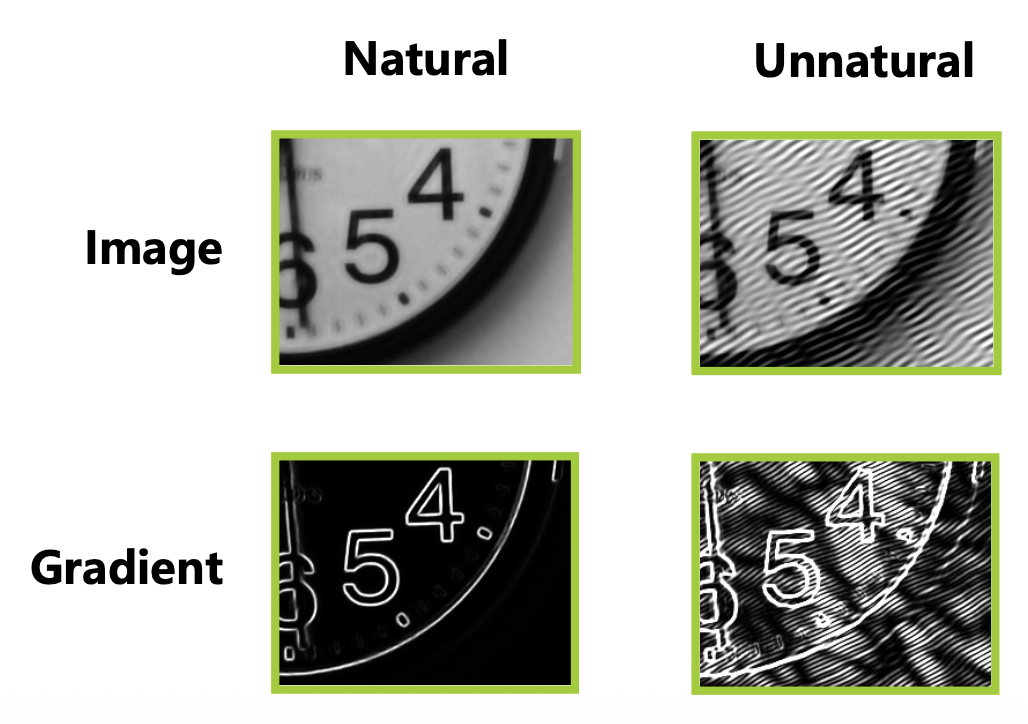
因此需要解的先验信息(prior information)。

• 自然图像在片段 (segments) 上通常平滑
• 梯度图是稀疏的
• 添加 L1 正则化使图像梯度稀疏

带先验信息的反卷积：目标函数 = 可能性函数 + 正则化项 $$ \min\limits_F |G - F \otimes H |_2^2 + |\nabla F|_1 $$

Blind Image Deconvolution (BID)⚓︎

盲图像反卷积(blind image deconvolution, BID)

• 卷积核也是未知的
• 这显然更难，因此需要更多的先验知识

核先验(kernel prior)：

• 模糊核是非负且稀疏的
• 优化目标函数

例子

以下是来自论文 Removing Camera Shake from a Single Photograph, SIGGRAPH 2006 的例子：

原始照片输出和模糊核

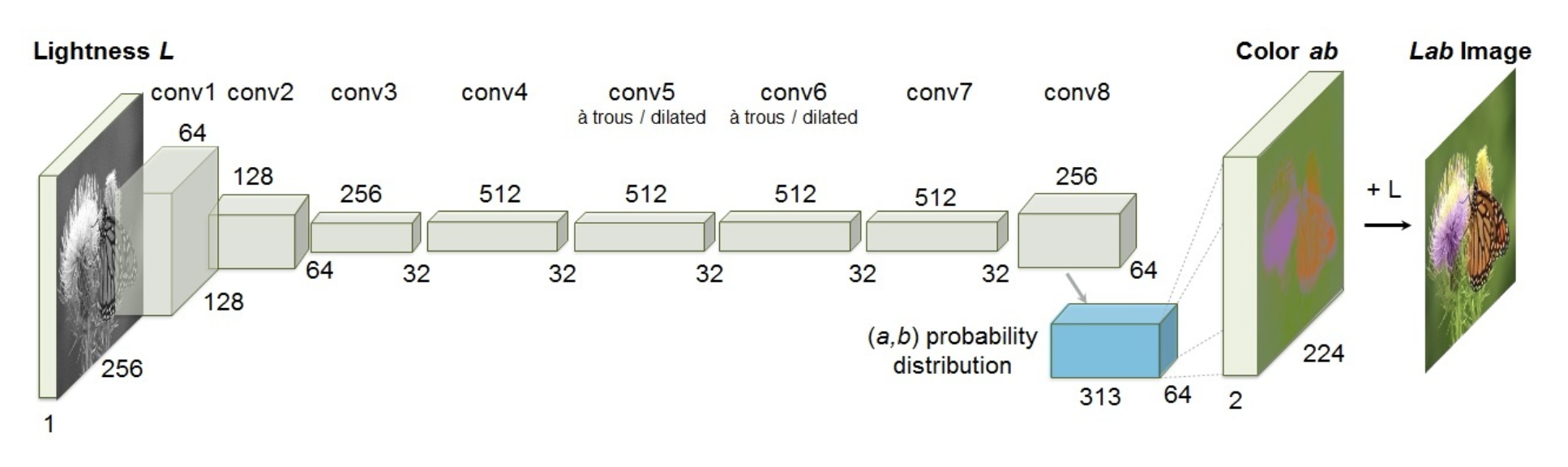
Colorization⚓︎

直到 1970 年，彩色照片仍然非常罕见，人们只能通过黑白照片回顾历史。如今，利用技术将黑白照片转换为彩色照片是一件轻而易举的事。

上色(colorization) 指借助计算机为单色图片或视频添加颜色的过程。

有两种主要的为灰度图像上色的方法：

• 基于样本的上色 (sample-based colorization)：使用样本图像

  

  扫描目标图像，对每个像素：

  • 在样本中找到最佳匹配点（比如考虑亮度与相邻像素的标准差 (standard deviation)）
  • 将匹配点的颜色分配给像素

• 交互式上色：用画笔交互式地绘制

  
  • 对于两个相邻的像素，如果亮度相似，那么颜色也应该保持相似

  • 基于这个假设，着色问题被转化为一个优化问题，相应的目标函数如下：

    \[ J(U) = \sum\limits_r \left(U(r) - \sum\limits_{s \in N(r)} w_{rs} U(s)\right)^2 \]
    • \(U(r), U(s)\)：像素 \(r, s\) 的 RGB 颜色
    • \(N(r)\)：像素 \(r\) 的邻居像素
    • \(w_{rs}\)：测量 \(r, s\) 相似度的权重

  • 约束条件：用户指定的笔刷像素颜色保持不变

  例子

  例 1 例 2：视频上色

  

  

  

Modern Approach⚓︎

CNN（链接：http://richzhang.github.io/colorization/）：

用于图像合成的损失函数：

• 重构损失：\(L(\Theta) = \|F(X; \Theta) - Y\|^2\)
• 问题：
  • 无法处理多解的情况
  • 无法测量图像的真实性

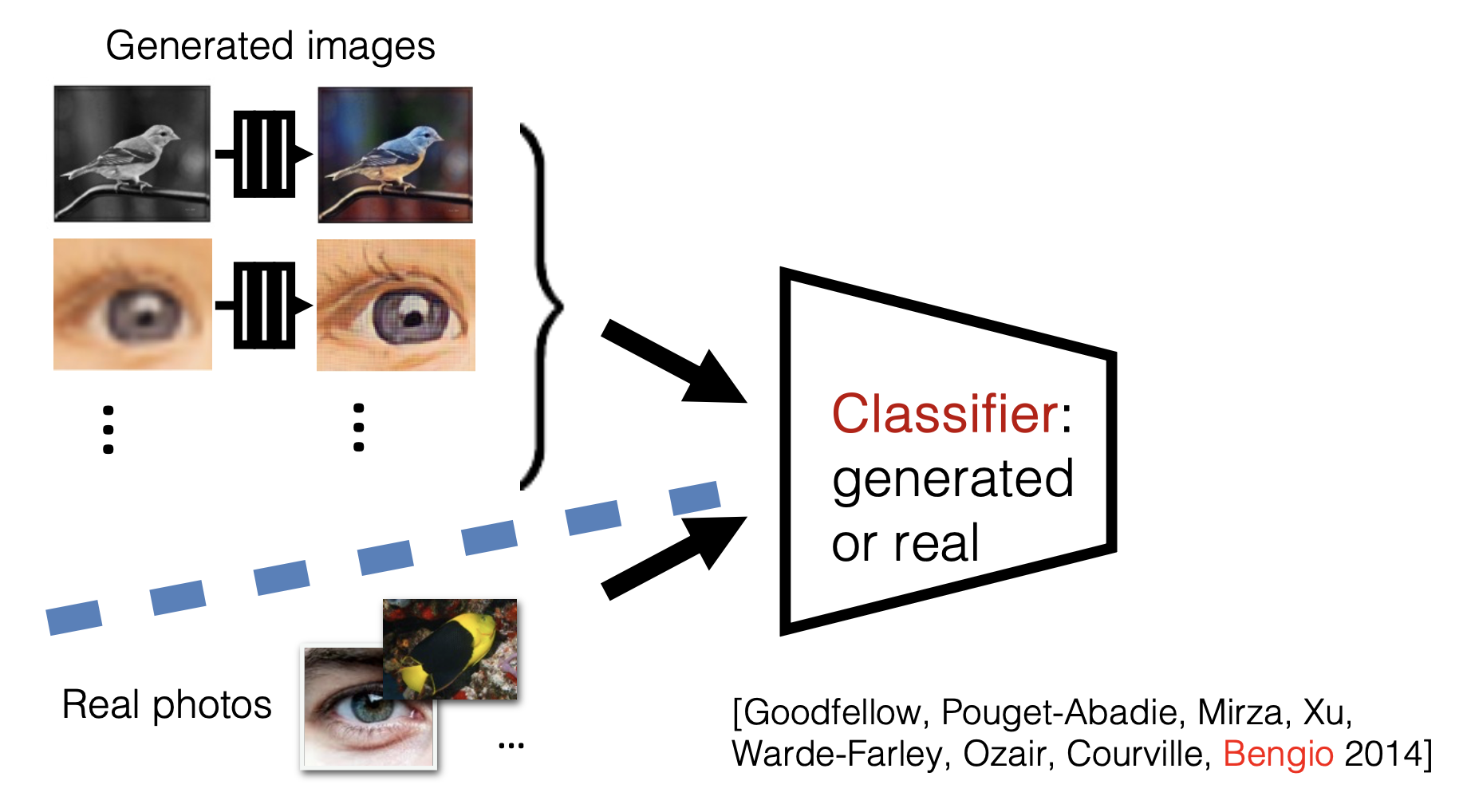
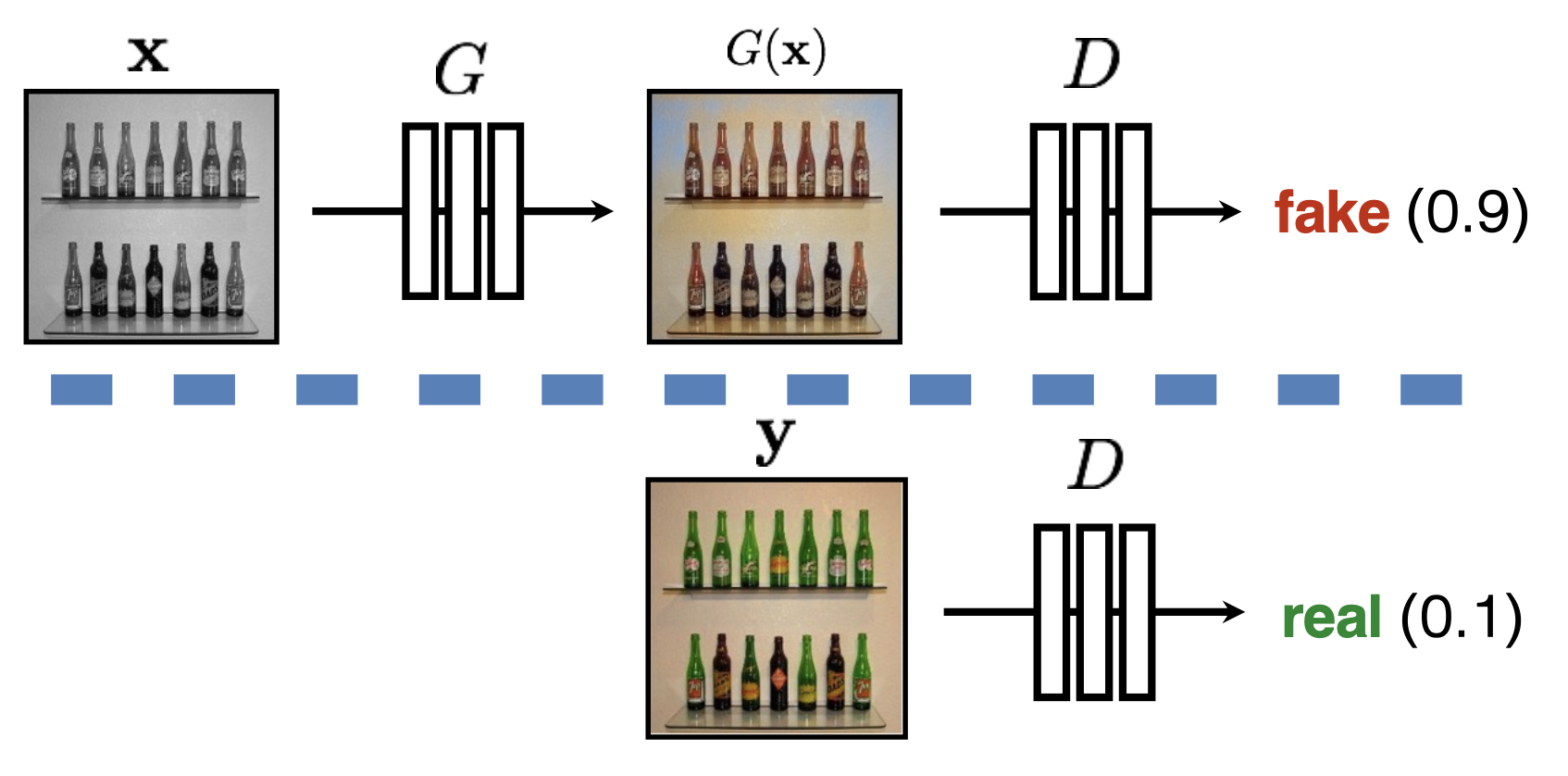
我们可以学习一个衡量图像是否真实的损失函数——利用生成式对抗网络(generative adversarial network, GAN)：

• G 尝试合成能够欺骗 D 的假图像

  • 而且是最好的 D
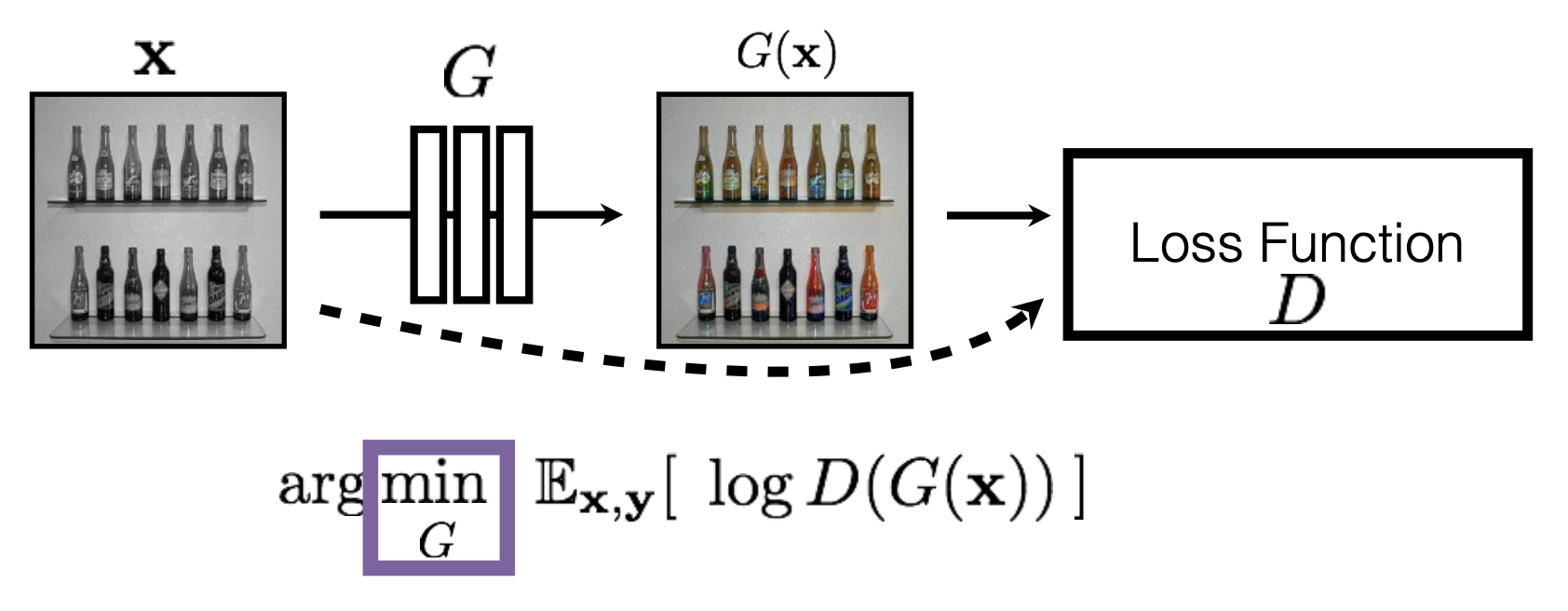
  \[ \arg\min_{G} \max_D \mathbb{E}_{\mathbf{x},\mathbf{y}} \left[ \log D(G(\mathbf{x})) + \log(1 - D(\mathbf{y})) \right] \]

• D 尝试识别出假图像

可以把 D 看做用于训练 G 的损失函数

• 称为对抗损失(adversarial loss)
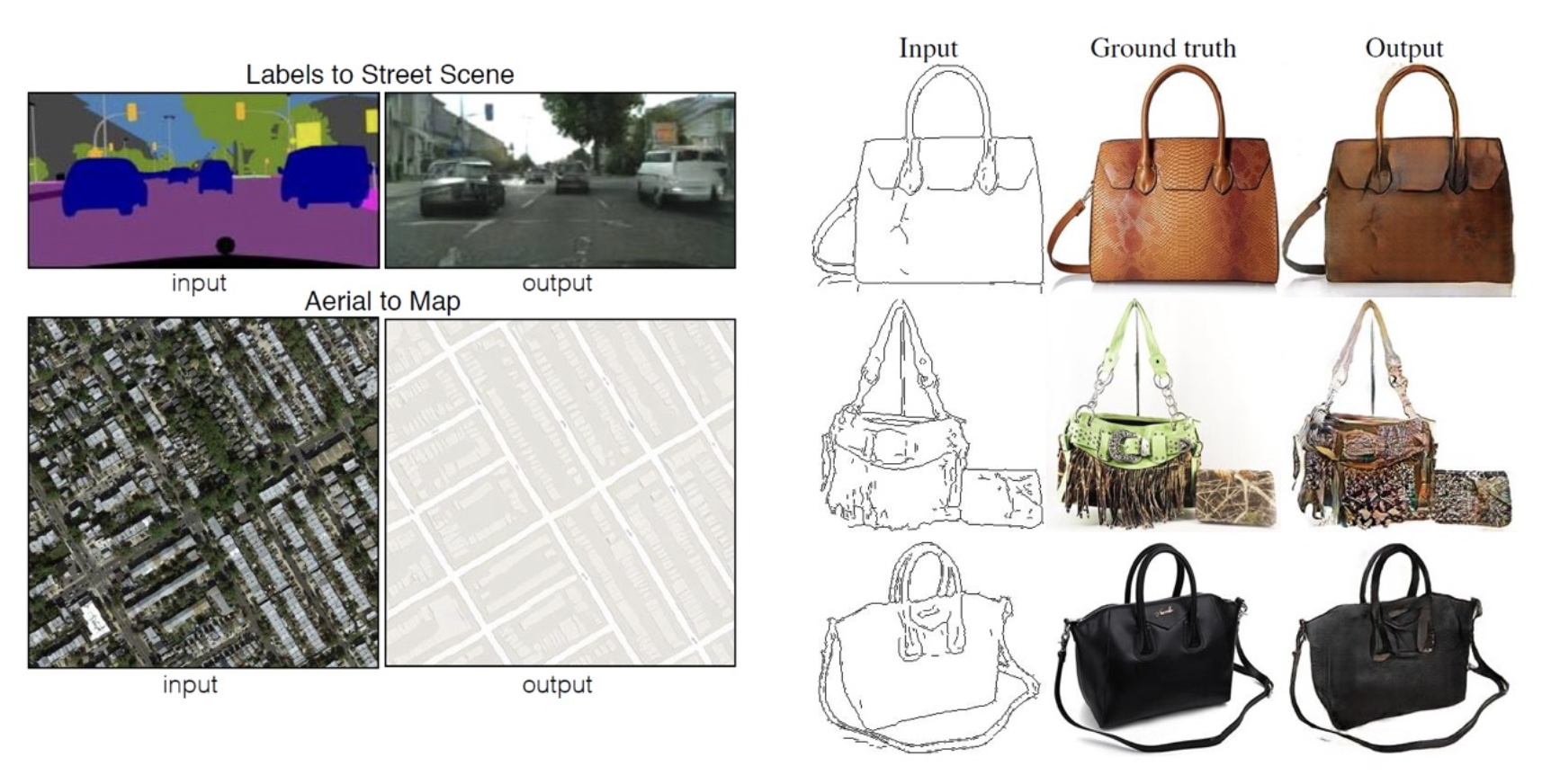
• 通过学习而非手工设计
• 可应用于任何图像合成任务

更多的图像合成任务

图生图风格迁移文生图图像去雾

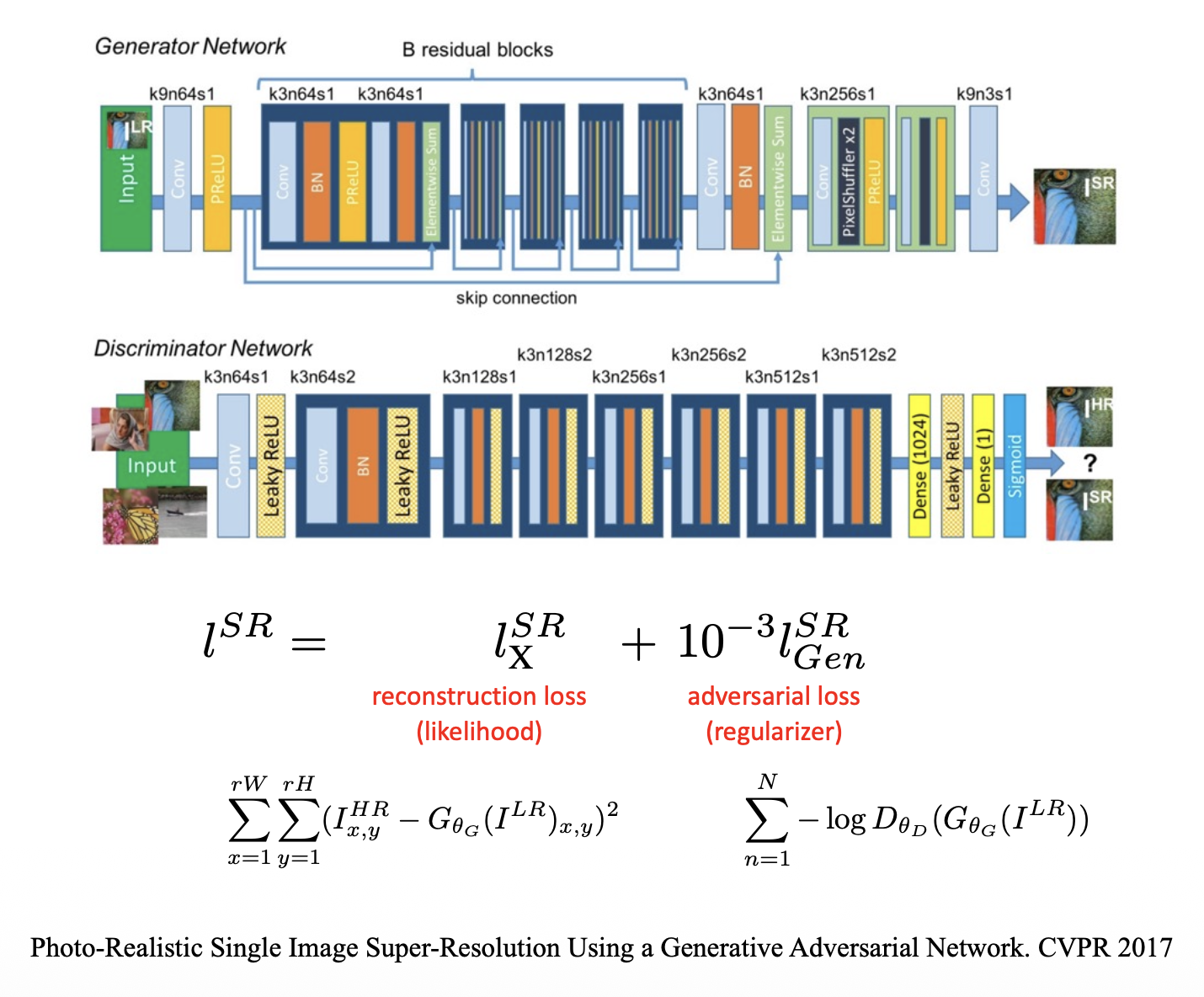
Super Resolution⚓︎

超分辨率(super resolution)：

利用 GAN 实现超分辨率：

效果：

评论区