Life-long Learning⚓︎

看到“终身学习”(life-long learning) 这样的标题，我们脑海中首先想到的可能是关于我们人类的终身学习，也就是“活到老，学到老”——不过本讲要介绍的是关于机器的终身学习。在还没学过机器学习相关知识前，我们对 AI 的想象也许是像下图这样：机器能一直从不同的任务重学习新技能，最终形成像《终结者》电影里的“天网”。

注：在机器学习中，终身学习还有像 continue learning, never ending learning, incremental learning 等同义词。

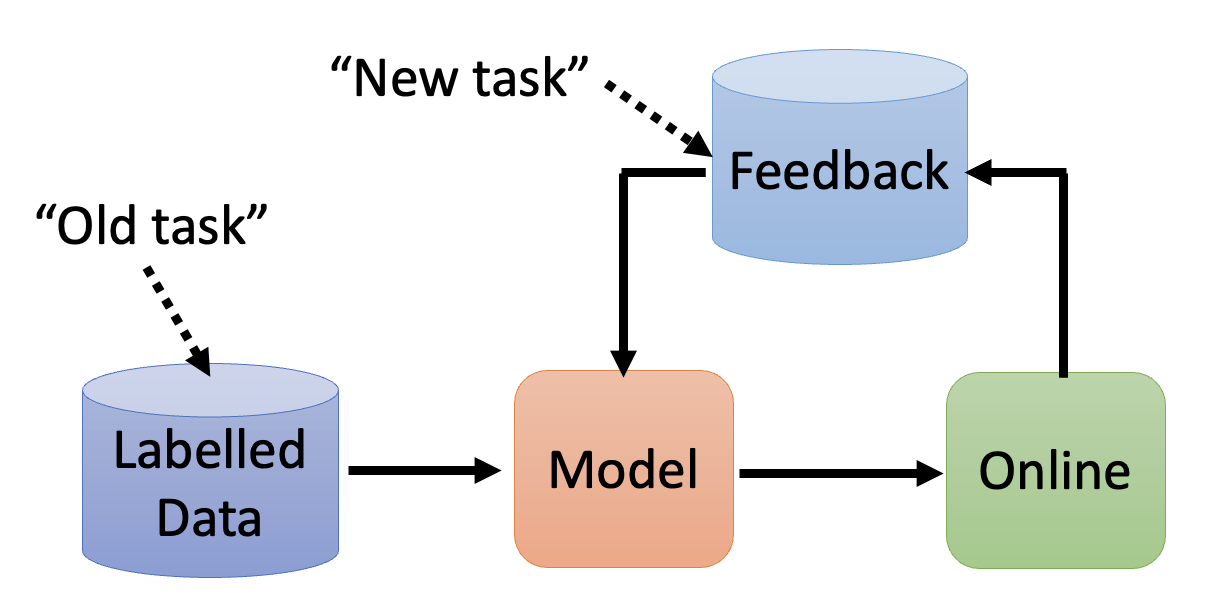
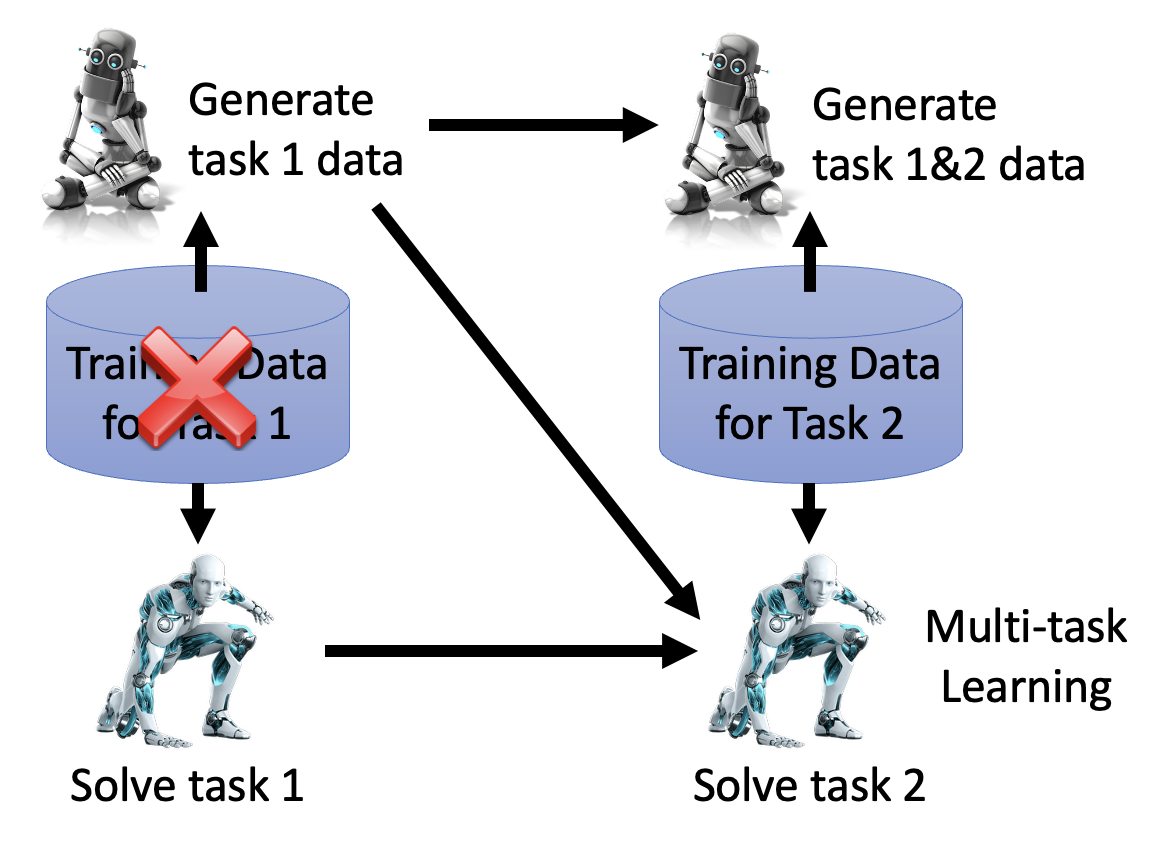
在现实应用中，终身学习的流程大概如下图所示那样：

例子

例 1 例 2

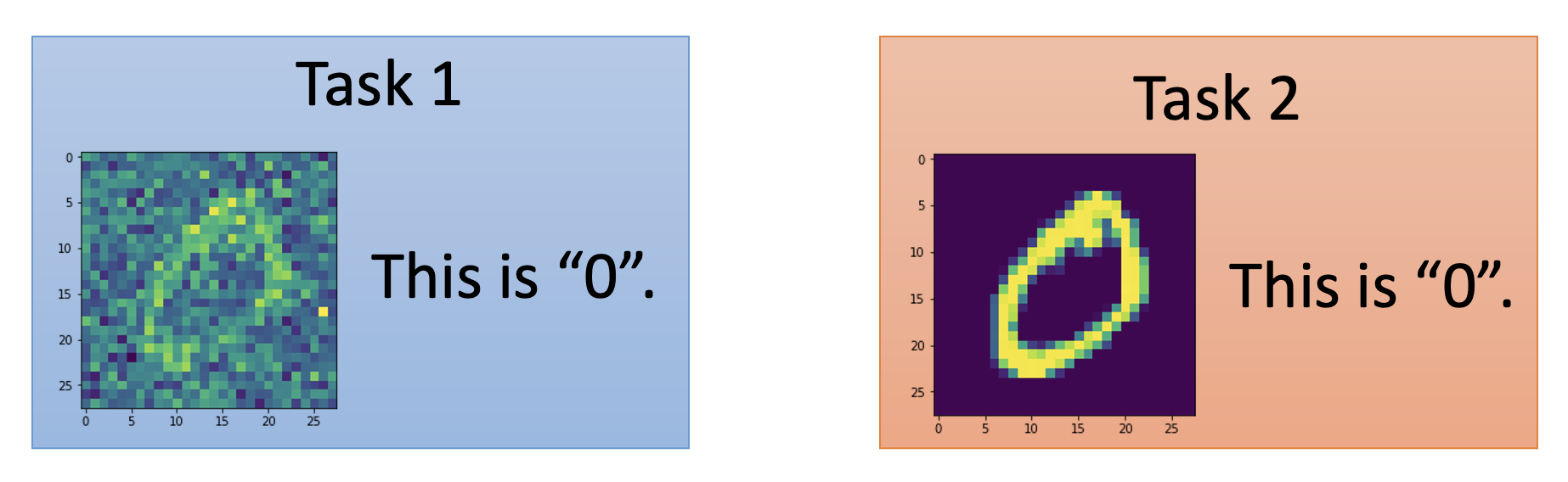
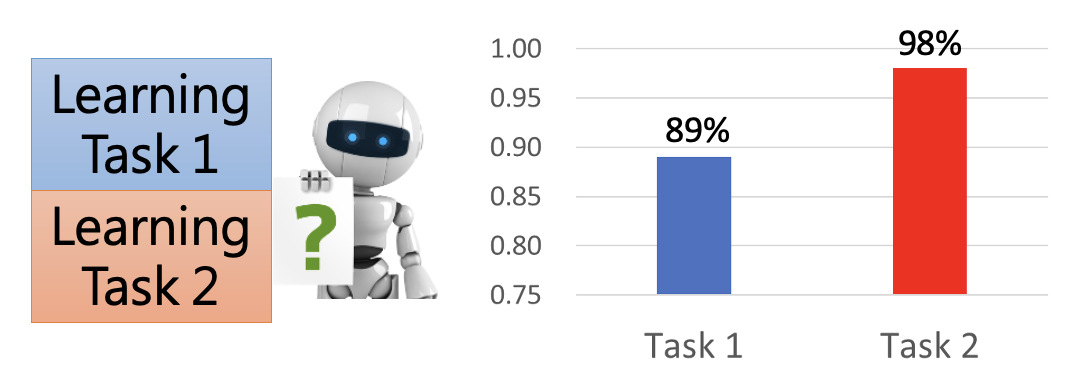
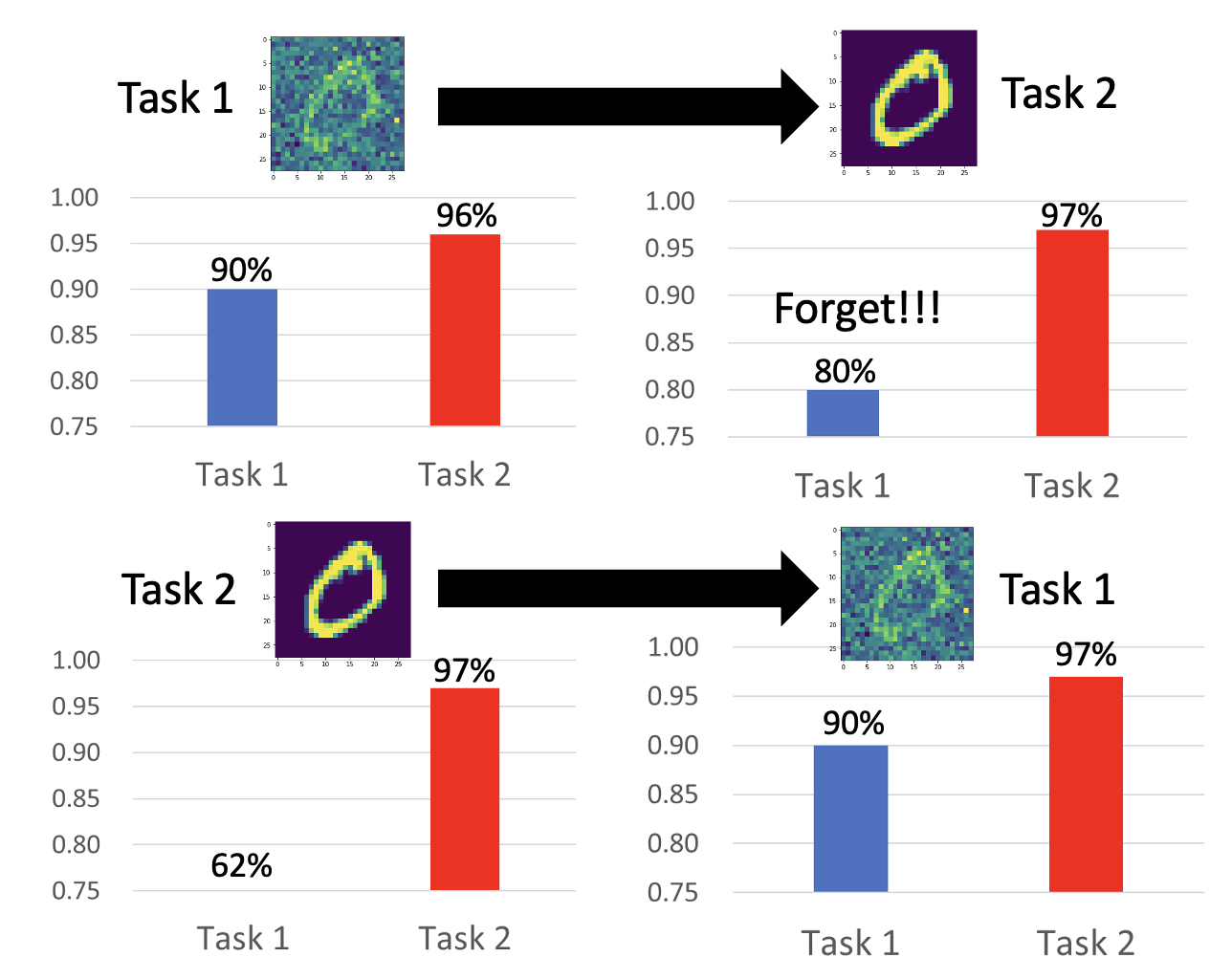
假如现在让一个简单的模型（只有 3 层，每层 50 个神经元）来完成下面两个手写数字识别任务：

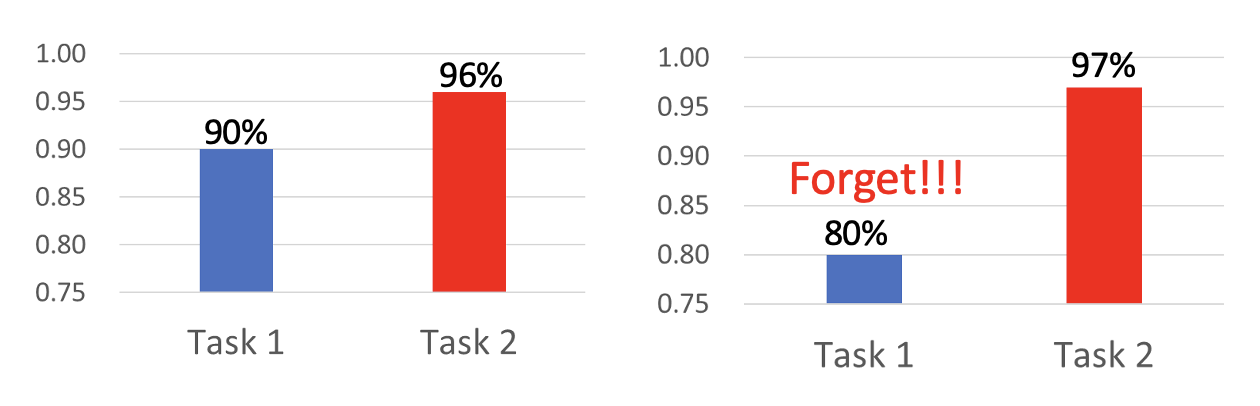
如果先用任务 1 训练，再用任务 2 训练，得到的结果如下：

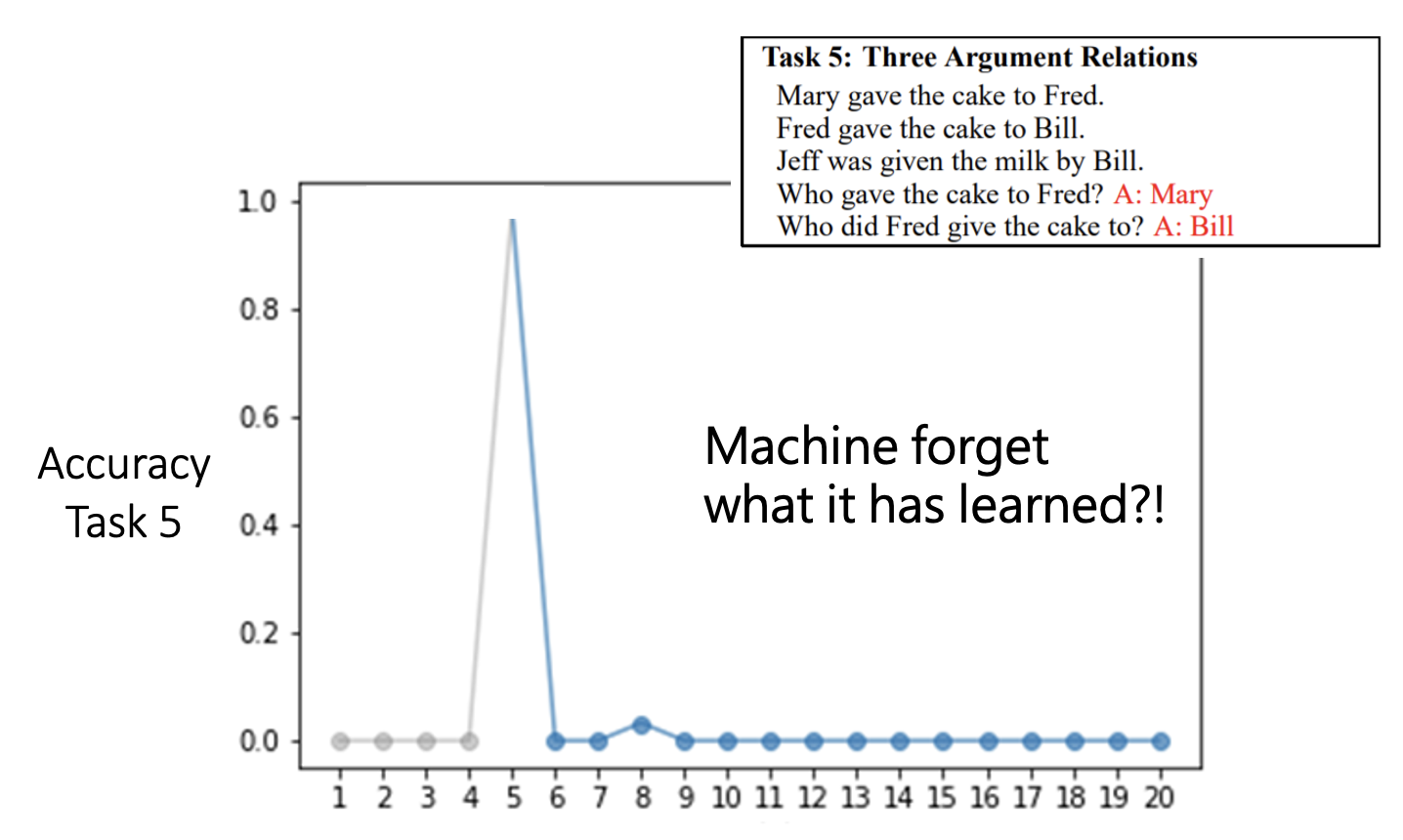
可以看到，模型能够仅根据任务 1 的训练掌握了一定的完成任务 2 的能力，而且接着在任务 2 上训练能够继续提升该能力。但是在任务 2 上训练后，模型在任务 1 上的能力是明显下降的，说明模型对任务 1 有所“遗忘”。

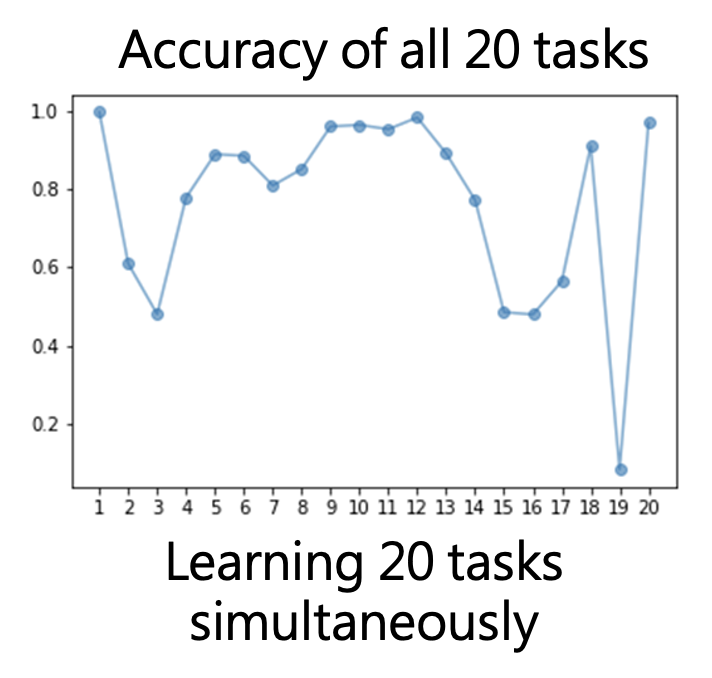
然而，如果让模型同时从任务 1 和任务 2 学习，那么模型能够在两个任务中同时取得不错的表现，这说明不是模型本身能力的不足，而是在一个接一个的训练中存在一些问题。

另一个例子是在 bAbi 语料库上训练一个 QA 模型，其中 bAbi 语料库包含了 20 个简单的 QA 任务，如下所示：

如果是按任务顺序一个个来训练模型的话，模型在任务 5 上的准确率如下所示，可以看到只有在训练完任务 5 的那一刻，模型才能在任务 5 上取得较高的准确率，而无论在之前（没有训练过）还是之后（忘记了）准确率都很低。

但如果让模型同时在 20 个任务上进行训练的话，模型在每一个任务上的准确率基本都很高。

这就说明了不是模型没能力学得更好，而是它没有做到这么好，正如孟子所说：“是不为也，非不能也。”

鉴于模型糟糕的记忆力，我们将这种现象称为灾难性遗忘(catastrophic forgetting)。

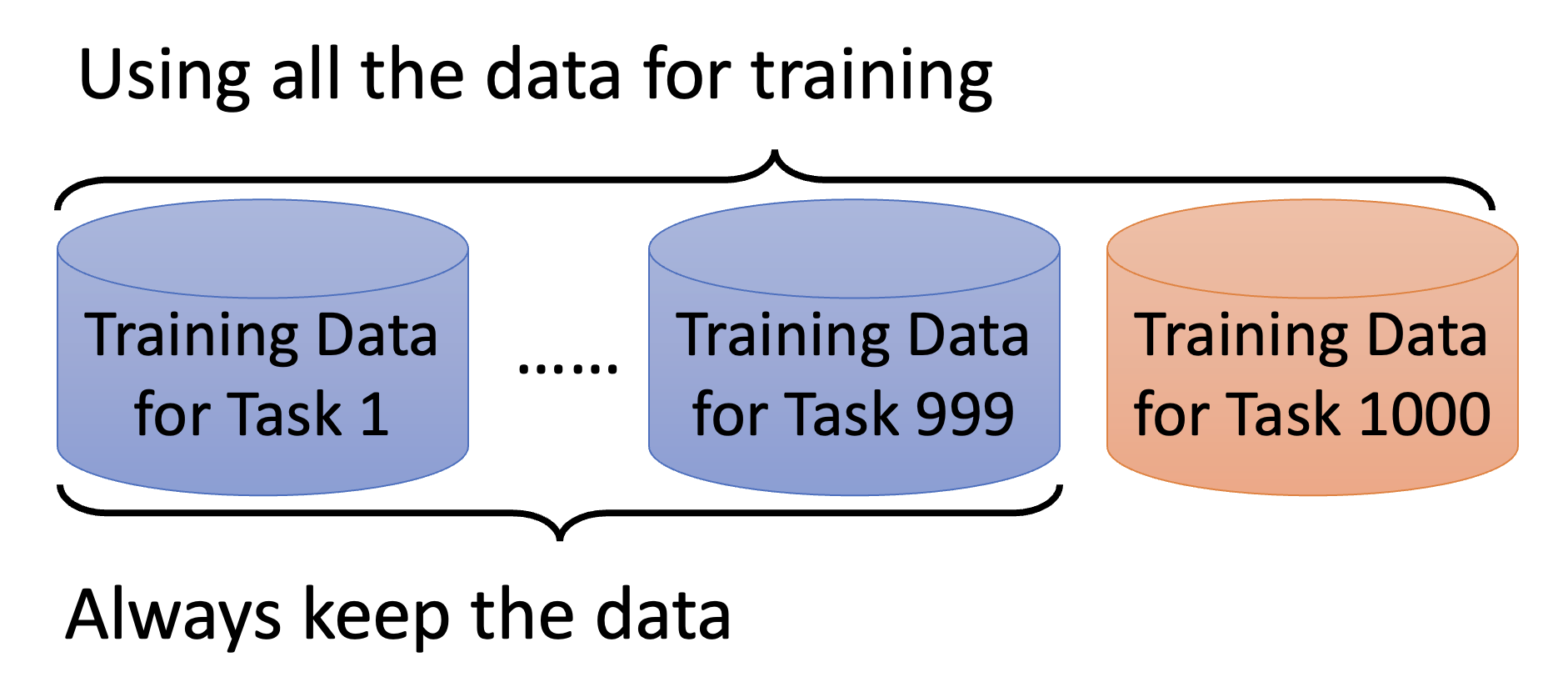
从前面的 2 个例子中不难发现，多任务训练(multi-task learning) 比所谓的终身学习效果更好，那为什么不这么做呢？

• 之前任务的数据都要保留下来，这会让存储空间变得更紧张
• 训练的时候要拿前面所有的数据一起训练，计算十分缓慢

不过由于多任务训练的效果更好，因此其结果常常作为终身学习的上界。

另一个思路是为每个任务训练不同的模型（“术业有专攻”）。

• 但每个模型都有各自的参数，也需要存储起来，一旦任务多起来后模型参数量就会很大，到最后也会更快耗尽存储空间。
• 还有一个问题是不同的模型无法迁移各自从不同任务中学到的知识，缺少“举一反三”的能力

终身学习和迁移学习(transfer learning) 的原理是差不多的，但最大的区别在于：

• 迁移学习要求在学完任务 1 后就能具备解决任务 2 的能力，至于机器之后还能不能完成任务 1 则不是我们要关心的
• 终身学习要求即便在学完任务 2 后，模型仍然具备完成任务 1 的能力

Evaluation⚓︎

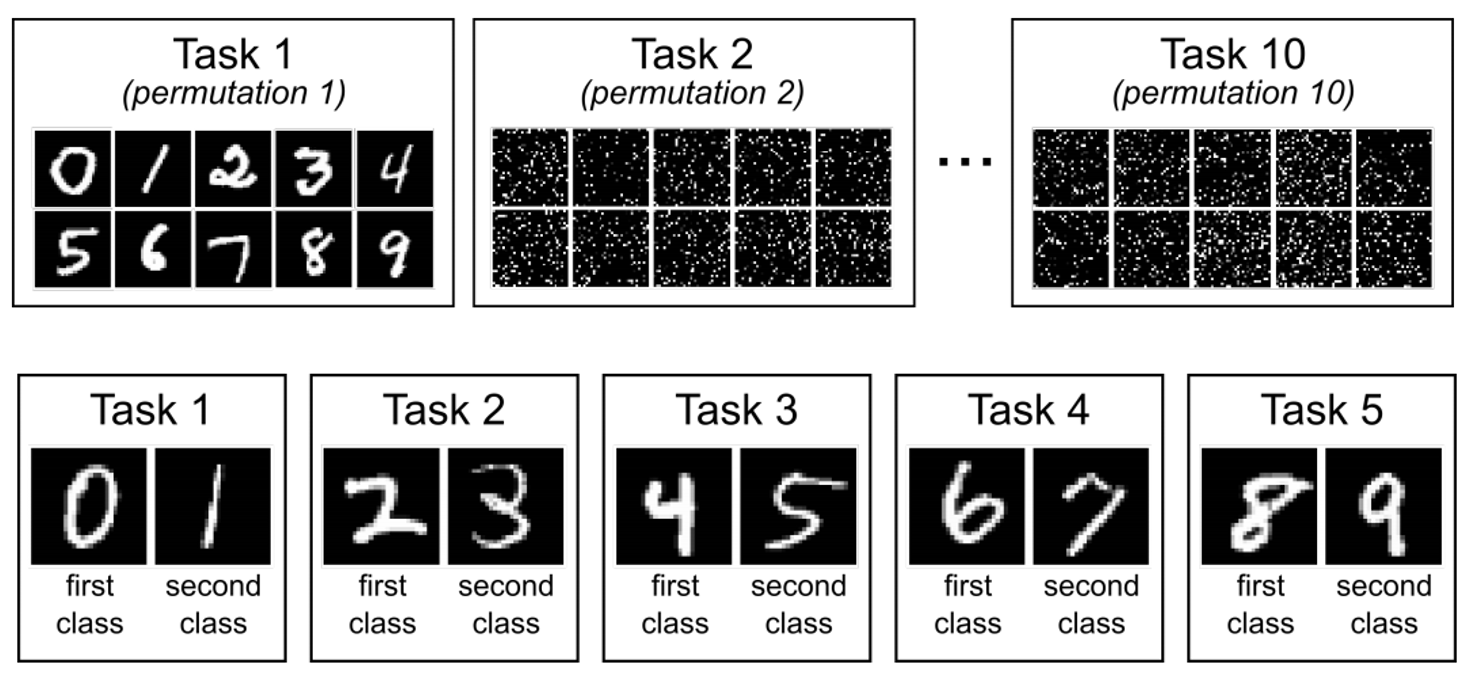
在评估终身学习的效果前，我们需要准备好一个任务序列，比如：

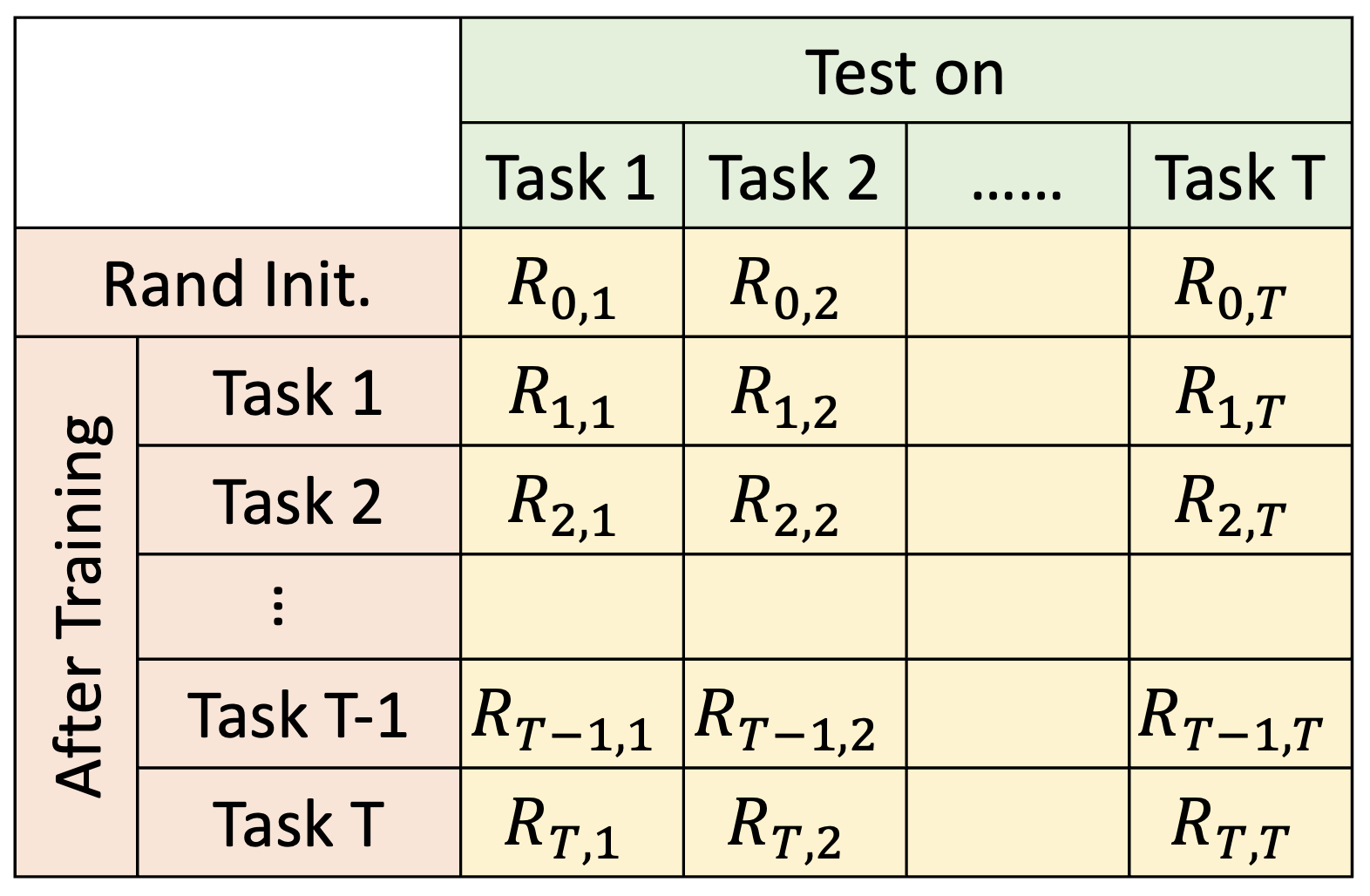
考虑更一般的情况：假如有 \(T\) 个待训练的任务，我们绘制了一个 \((T + 1) \times (T + 1)\) 大小的表格，每个单元格 \(R_{i, j}\) 代表在完成任务 \(i\) 的训练后，模型在任务 \(j\) 上的表现。

• \(i > j\)：\(R_{i, j}\) 表明在训练完任务 \(i\) 后模型是否忘了任务 \(j\)
• \(i < j\)：\(R_{i, j}\) 表明模型是否能将任务 \(i\) 的训练成果迁移到任务 \(j\) 上

常见的评估方法有：

• 平均值：\(\dfrac{1}{T} \sum\limits_{i=1}^T R_{T, i}\)（仅看表格最后一行）

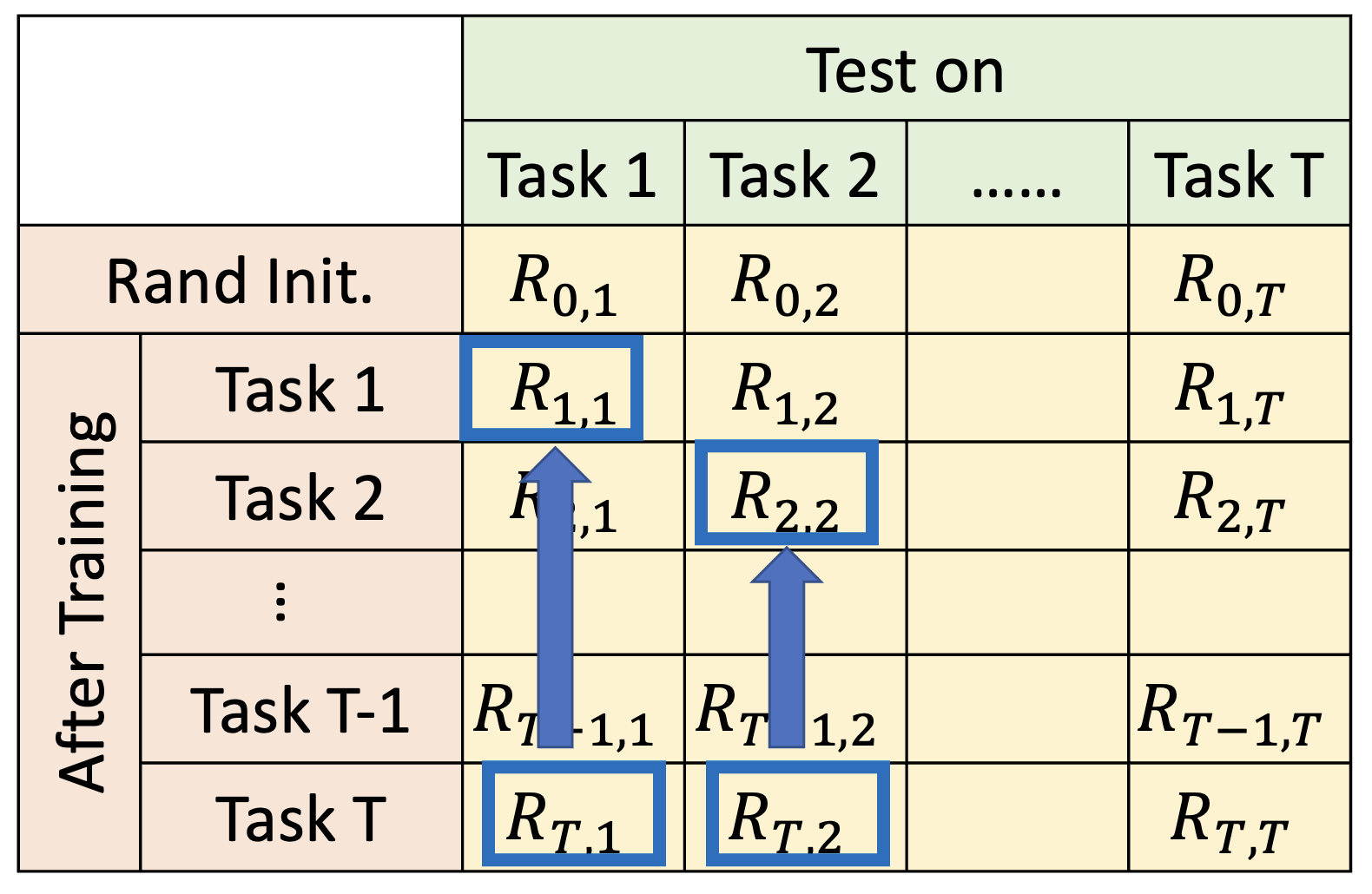
• 后向迁移(backward transfer)：\(\dfrac{1}{T-1} \sum\limits_{i=1}^{T-1} R_{T, i} - R_{i, i}\)

  • 显然这个值通常为负（如果读者能找到让这个值为正的技术，那就很 nb 了）
  

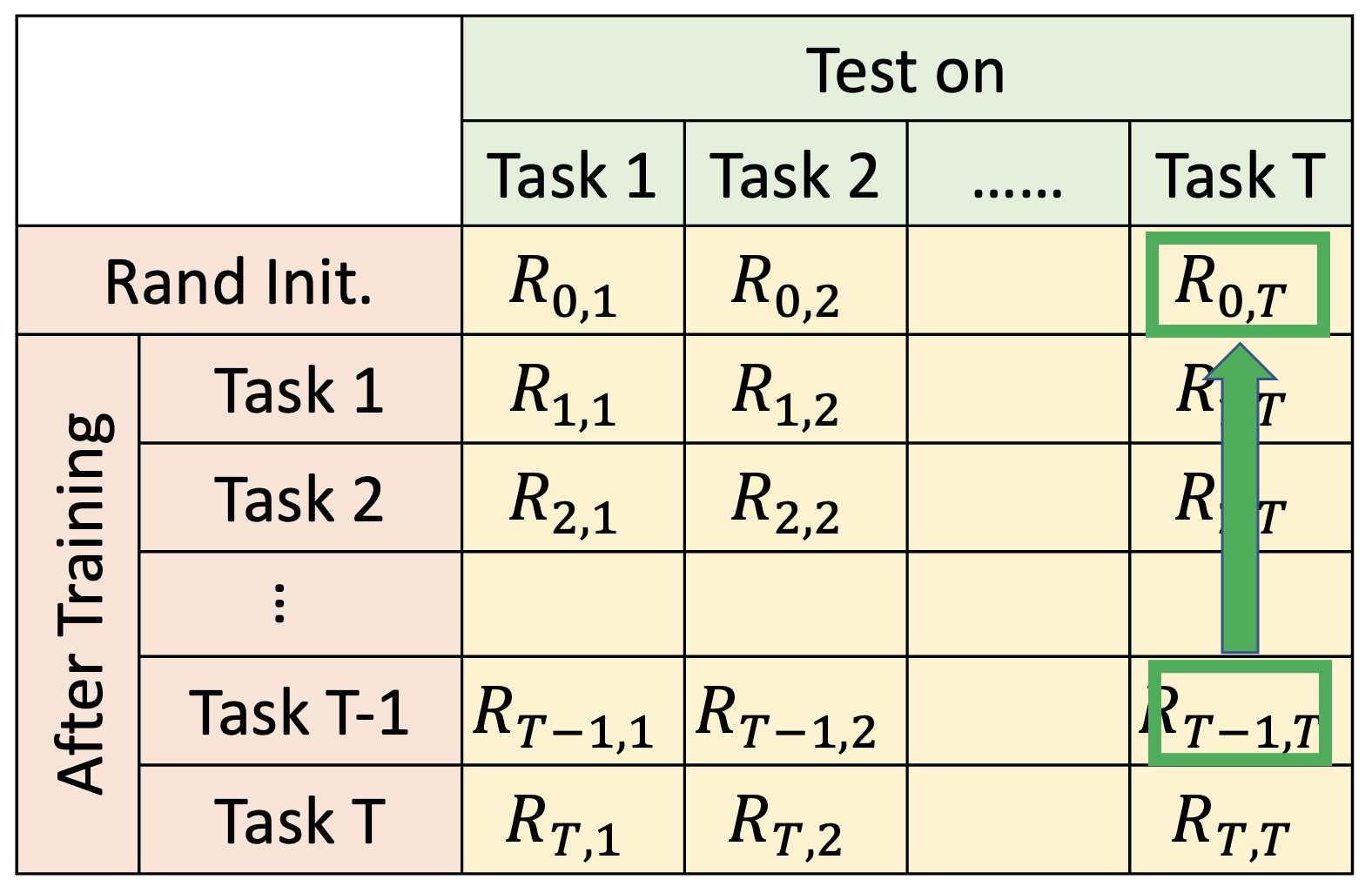
• 前向迁移(forward transfer)：\(\dfrac{1}{T-1} \sum\limits_{i=2}^{T} R_{i - 1, i} - R_{0, i}\)

  

接下来将介绍三个常见的研究方向～

Selective Synaptic Plasticity⚓︎

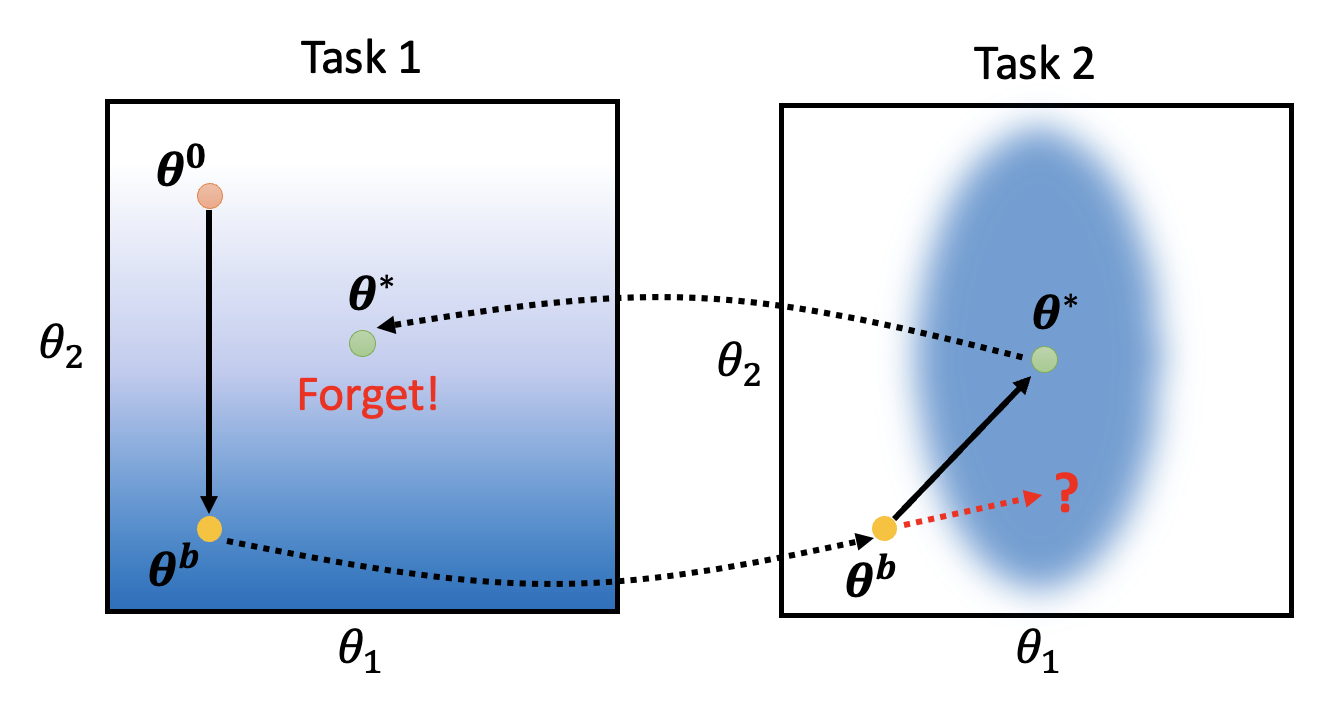
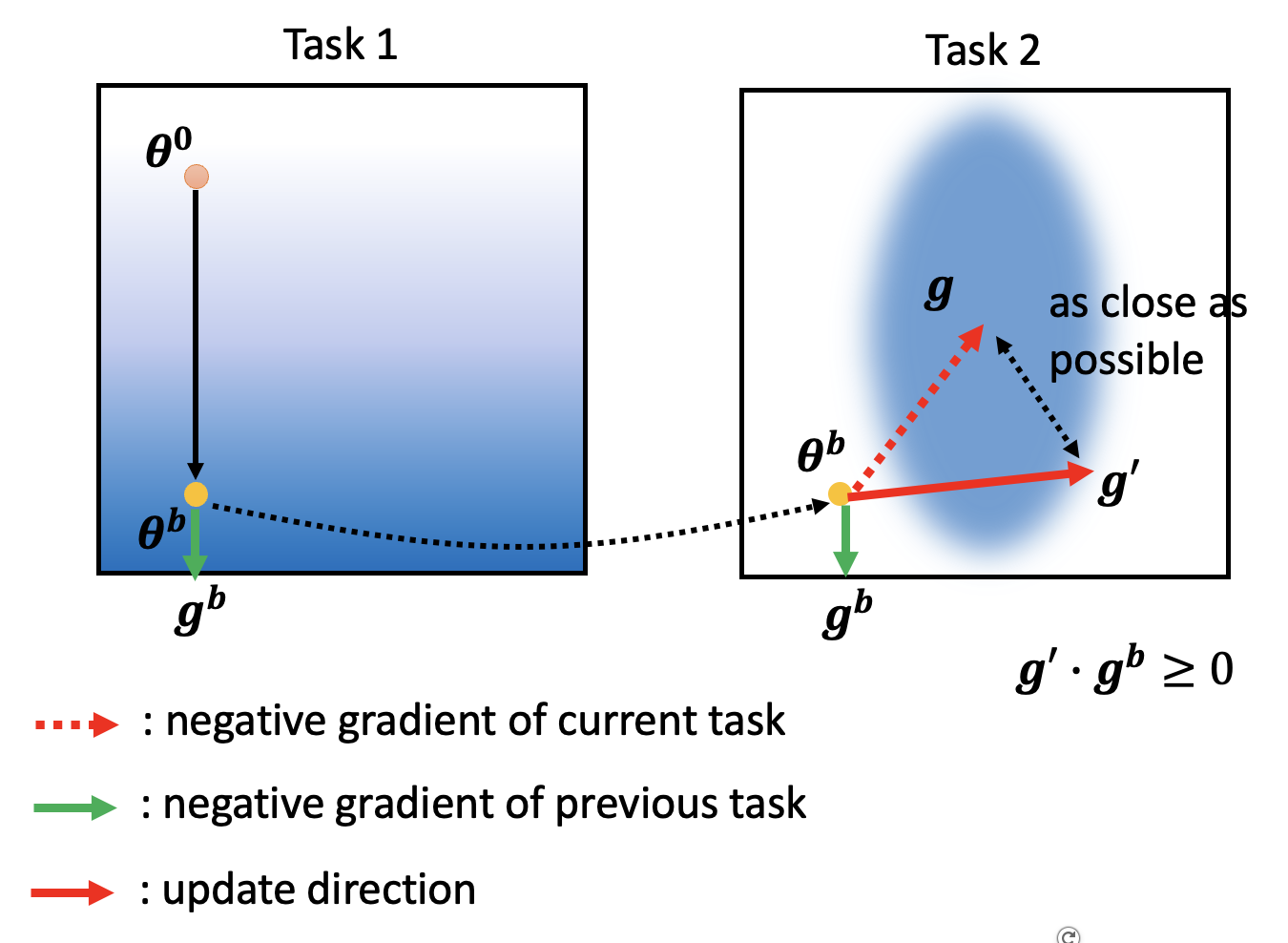
先来看为什么会出现灾难性遗忘的现象。考虑一个很简单的例子：模型只有两个参数 \(\theta_1, \theta_2\)。在任务 1 中，初始参数为 \(\bm{\theta}^0\)，训练结束后参数为 \(\bm{\theta}^b\)。接着将在任务 2 上训练该模型（仍然沿用刚训练得到的参数），训练后得到参数 \(\bm{\theta}^*\)。这个时候就出现了一个问题：\(\bm{\theta}^*\) 在任务 1 中并不是最优参数，甚至有可能让模型在任务 1 中表现很烂，也就是说模型忘记了它在任务 1 中习得的能力。

下图展示了模型在两个任务中的误差曲面，其中颜色越蓝表明损失越小：

要是模型在任务 2 的训练中能够沿红色虚线箭头前进，那么它就能保证其原来解决任务 1 的能力。

其中一个解决方案叫做选择性突触可塑性(selective synaptic plasticity)，它是一种基于正则化的方法 (regularization-based approach)。它的基本思想是：只有部分参数对之前的任务来说是重要的，所以只需改变那些不重要的参数。假设 \(\bm{\theta}^b\) 为模型从先前任务中习得的参数，并且令每个参数 \(\theta^b_i\) 都有一个“守卫” \(b_i\)。那么重新定义损失函数为：

• \(L'(\bm{\theta})\)：将要被优化的损失
• \(L(\bm{\theta})\)：当前任务的损失
• \(b_i\)：“守卫”，反映第 \(i\) 个参数的重要程度
• \(\theta_i\)：将要学习的参数
• \(\theta_i^b\)：从之前任务中习得的参数
• 因而 \(\sum\limits_i b_i (\theta_i - \theta_i^b)^2\) 反映了 \(\bm{\theta}, \bm{\theta}^b\) 之间在某个方向上要有多近
  • 灾难性遗忘：若 \(b_i = 0\)，\(\theta_i\) 没有任何约束（反正无论多大这项都没有影响）
  • 固执(intransigence)：若 \(b_i = \infty\)，\(\theta_i\) 和 \(\theta_i^b\) 应当始终相等

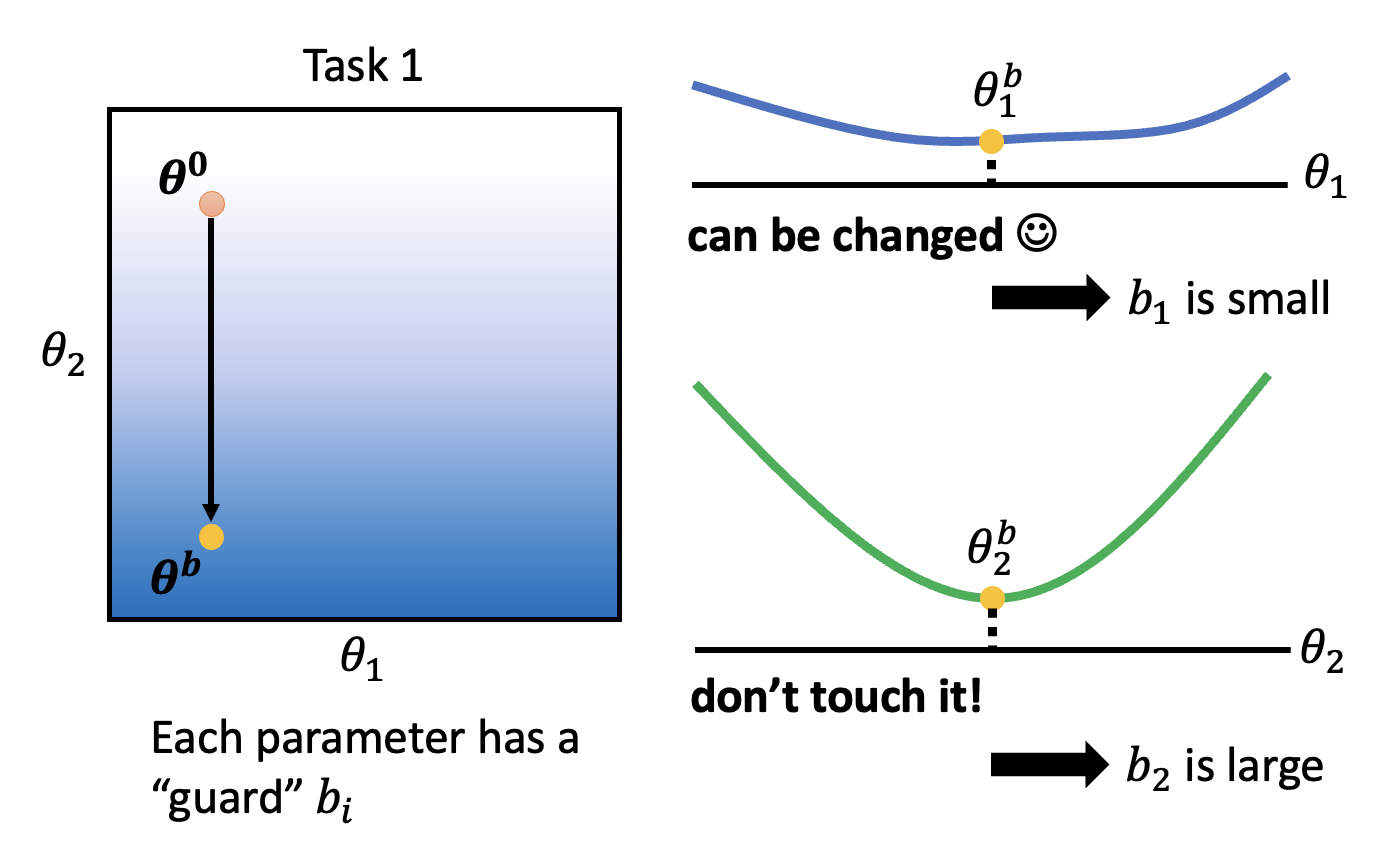
那么接下来要讨论的问题是如何寻找合适的 \(b_i\)？下面仍然通过前面的例子来讲述大致的思路。假如已经在任务 1 上找到最优参数 \(\bm{\theta}^b\)。从这个点出发，沿 \(\theta_1\) 方向看，损失没有太大的变化，说明这个参数不重要，是可以改变的，因而 \(b_1\) 比较小；但沿 \(\theta_2\) 方向看，损失变化明显，表明它是重要参数，\(b_2\) 应当大一些。

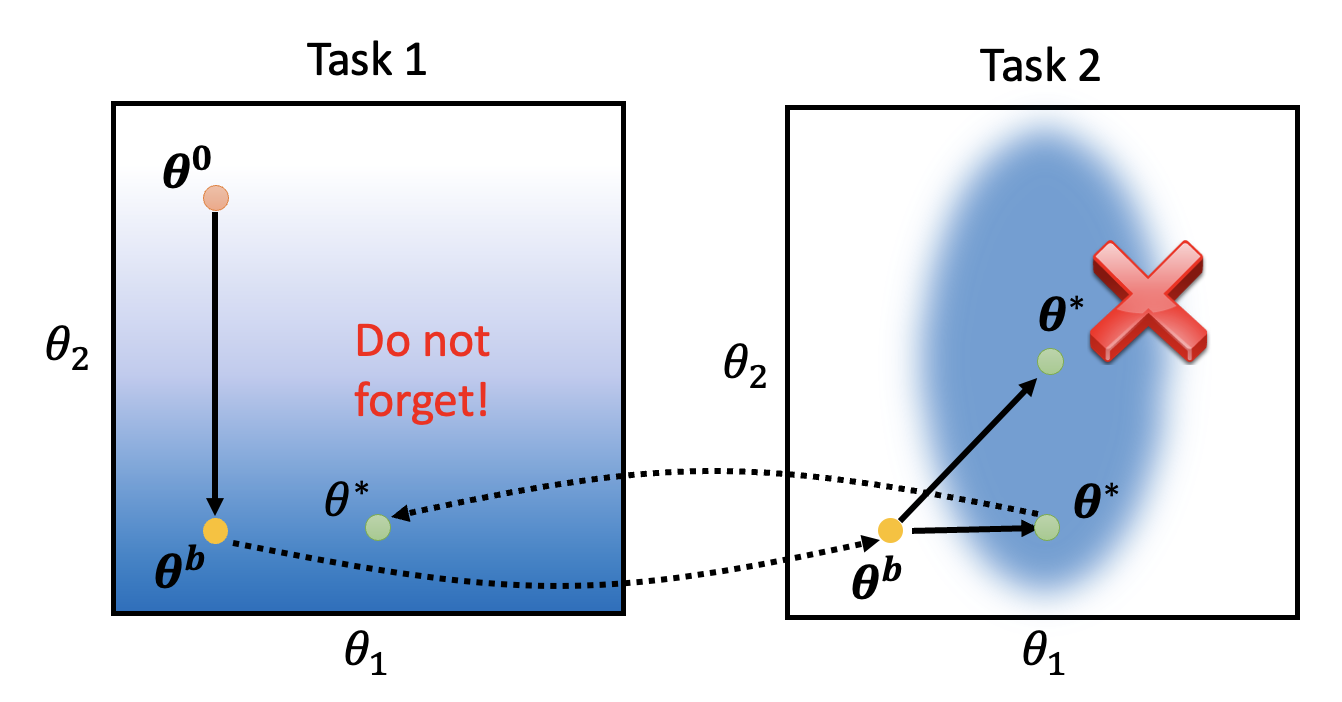
有了上面的发现后，在任务 2 上训练模型的时候就要有意地让模型尽可能沿 \(\theta_1\) 方向变化而不是沿 \(\theta_2\) 方向，这样模型可以兼顾两个任务上的能力。

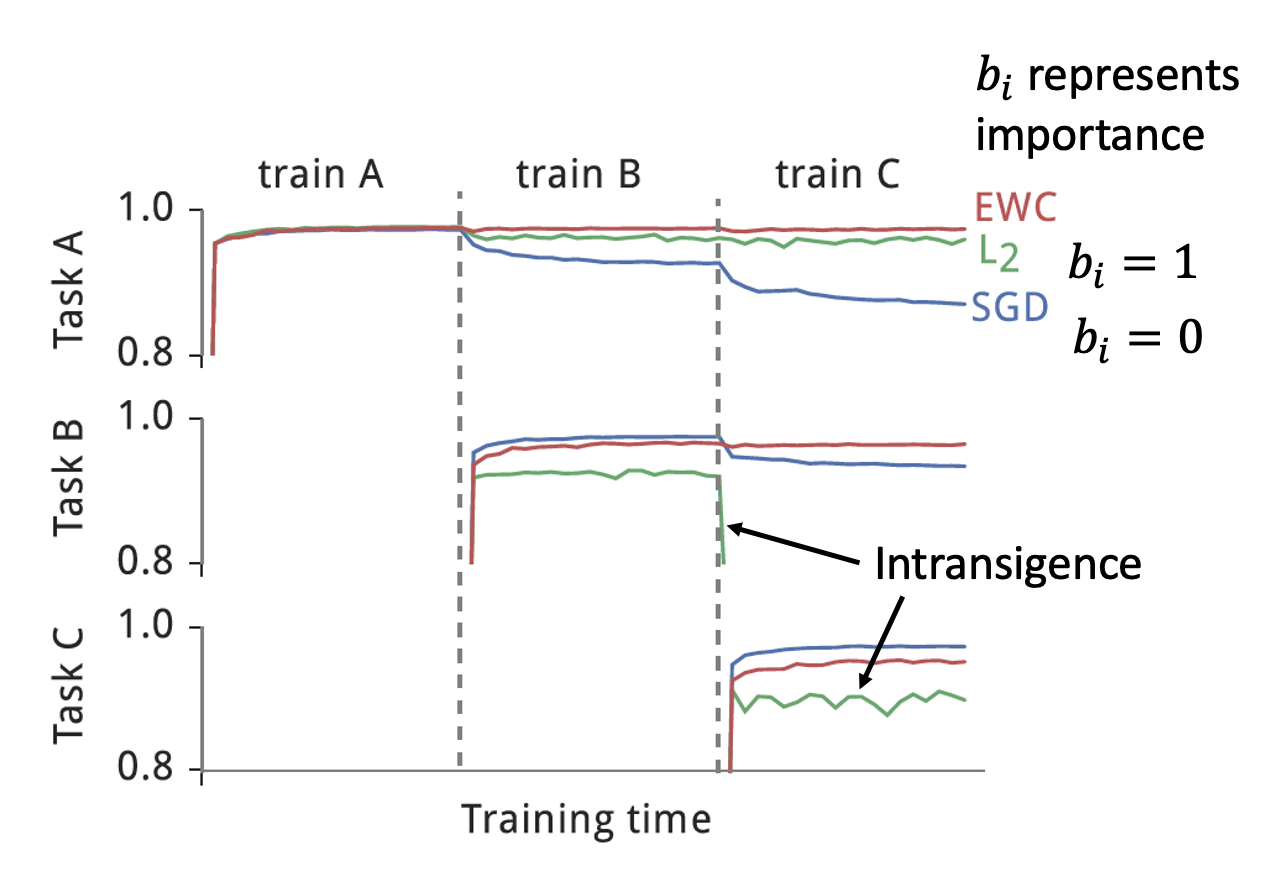
下面来看这种方法的效果。

• 蓝色曲线为 \(b_i = 0\) 的情况（就是一般的梯度下降法）
  • 蓝色曲线随训练任务的继续，会逐渐遗忘解决先前任务的能力
• 绿色曲线为 \(b_i = 1\) 的情况
  • 可以看到绿色曲线多数情况下处在偏下的准确率，说明它学习新本领的能力不足（有些“固执”）
• 红色曲线就用到了现在这种方法，虽然表现不一定是最好的，但是最稳定

相关研究：

• Elastic Weight Consolidation (EWC)
  • 上面的实验结果来自这篇论文
• Synaptic Intelligence (SI)
• Memory Aware Synapses (MAS)
• RWalk
• Sliced Cramer Preservation (SCP)

还有一种基于正则化的方法叫做梯度情景记忆(gradient episodic memory, GEM)，它的大致思路是让训练先前任务的梯度影响训练当前任务的梯度。但这种方法的问题在于它需要先前任务的数据，会占据更多空间。不过如果需要的数据量不大，那还是可以接受的。

Additional Neural Resource Allocation⚓︎

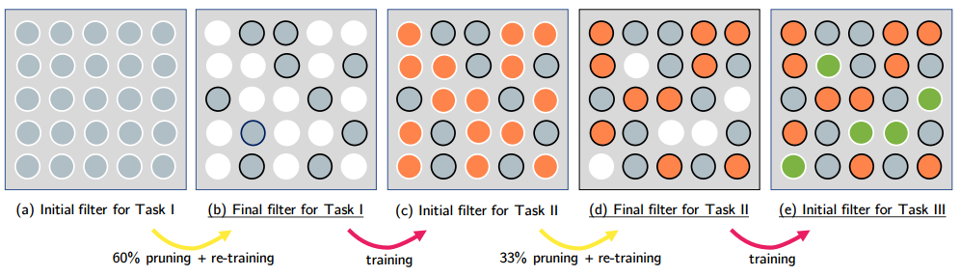
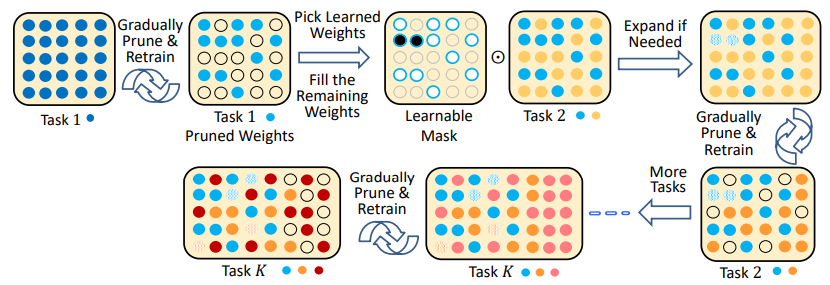
第二个方向是尝试改变每个任务中对神经元的资源分配，具体有以下可行的做法：

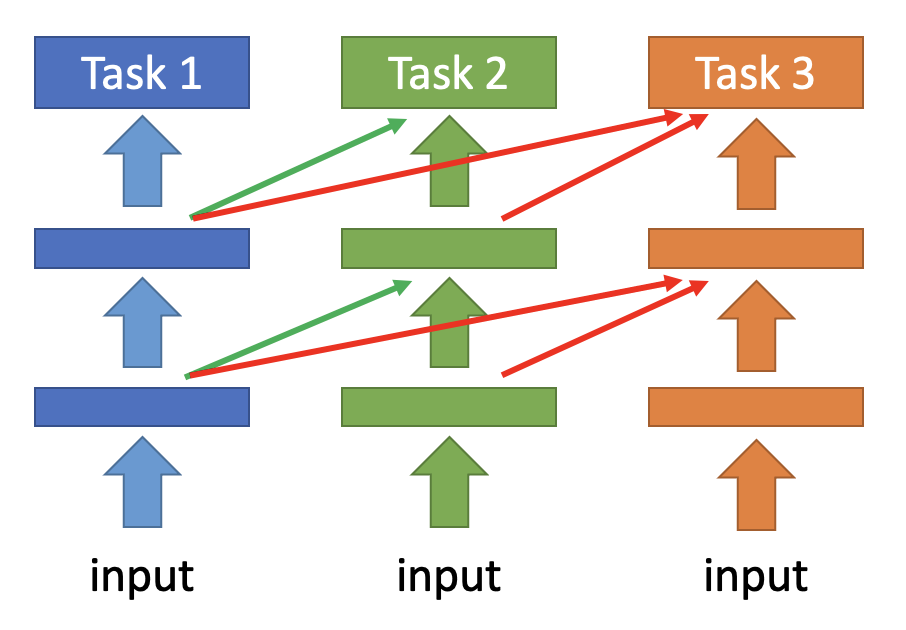
• 渐进神经网络 (progressive neural network)：每多训练一个任务，就往原来的模型中增添更多的参数，并保留先前任务中训练得到的参数

  

• PackNet

  

• Compacting, Picking, and Growing (CPG)

  

Memory Replay⚓︎

前面讲过，要是能集中所有任务的数据，那模型就不会出现灾难性遗忘的现象，但又规定不能保留先前任务的数据。我们可以从这个看似自相矛盾的要求中寻求一个平衡：额外训练一个生成模型（注意它也会占据一定空间），根据先前任务生成一些伪数据 (pseudo-data)。这样模型就能从包含多个任务，但是量不大的伪数据中继续学到解决先前任务的能力了。

相关研究链接：

• https://arxiv.org/abs/1705.08690
• https://arxiv.org/abs/1711.10563
• https://arxiv.org/abs/1909.03329

Others⚓︎

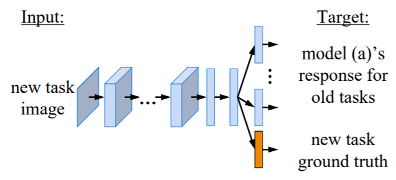
前面介绍的模型过于简化，其中一个忽略的点是每个任务要求的分类数量可能是不同的（而我们默认是一样的），所以有以下研究专门解决这个问题：

• Learning without forgetting (LwF)

  

• iCaRL: Incremental Classifier and Representation Learning

  

本讲只介绍了最简单的一类情况，其实还有两类更有挑战性的情况，感兴趣的读者可阅读论文 Three scenarios for continual learning。

也许读者已经注意到，任务的顺序对终身学习而言也是有不小影响的，有时可能因为任务顺序的改变，模型准确率就能有一些提升。

有关这一主题的研究叫做课程学习(curriculum learning)（什么鬼名字？）。