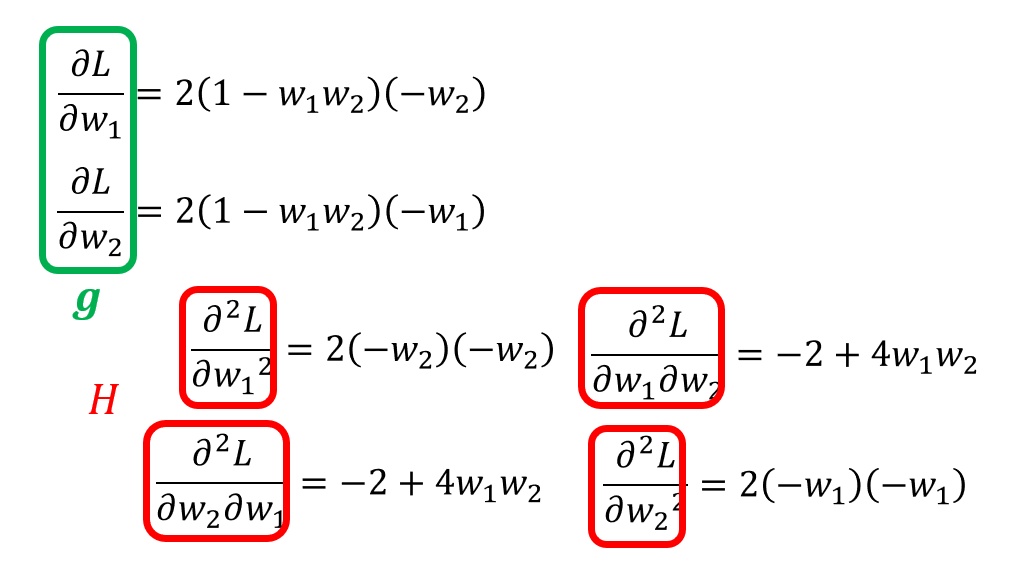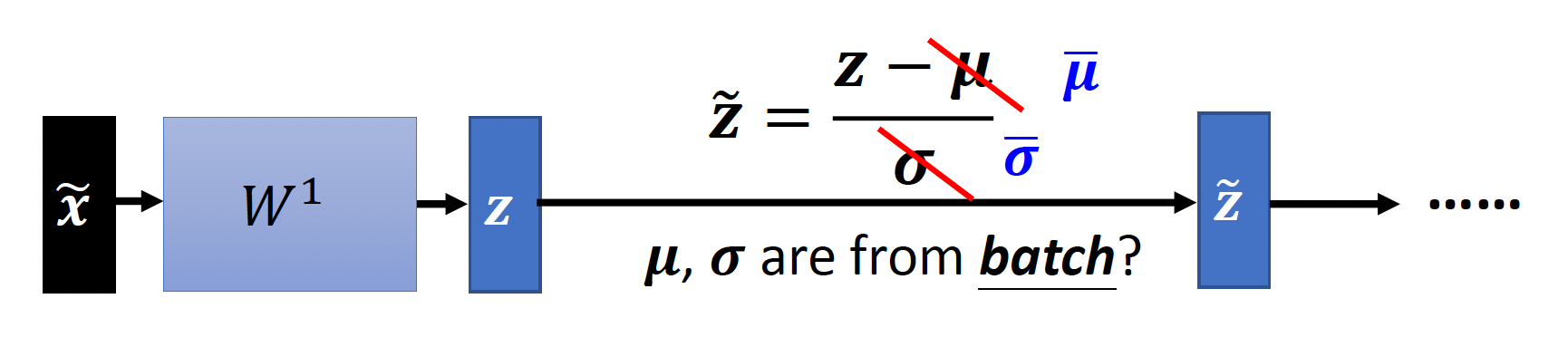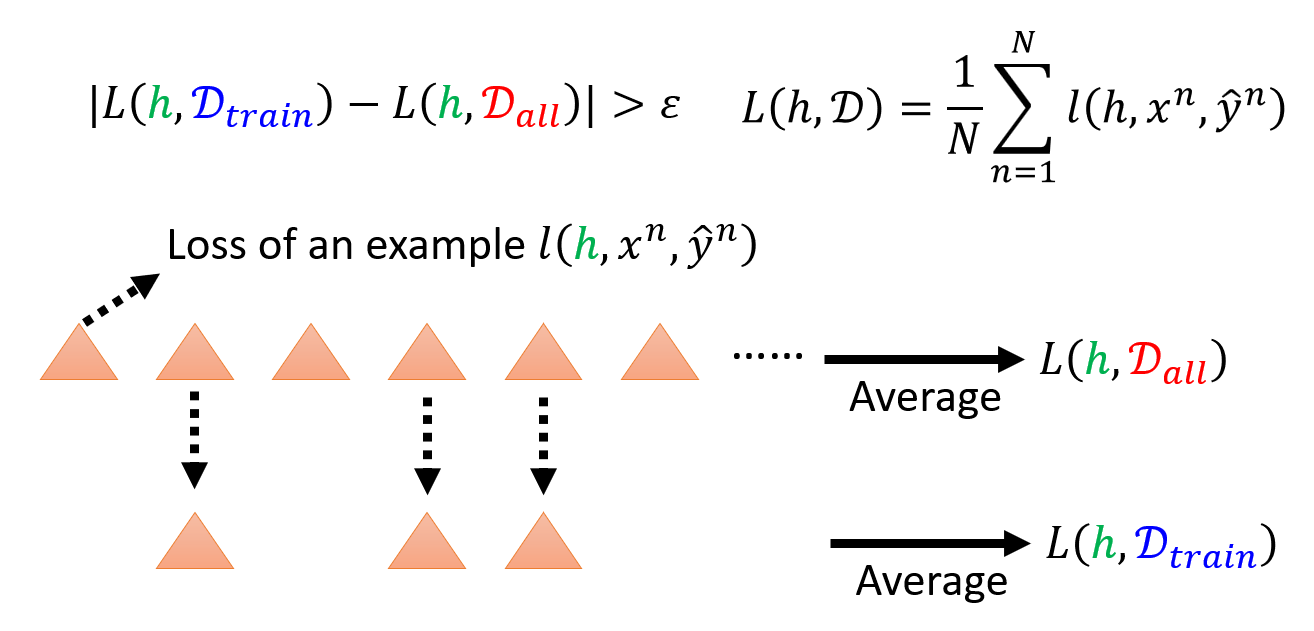Machine Learning - P2⚓︎

More Insight into Optimization⚓︎

Backpropogation⚓︎

在机器学习中，未知参数 \(\theta = \{w_1, w_2, \dots, b_1, b_2, \dots\}\) 通常会包含很多项。在使用梯度下降法时，每次都要对里面的每一项求偏微分；而且如果训练多次的话，计算量就会变得相当地大，因而效率就很低了。为了提高计算的效率，我们引入了一种新的计算技巧：反向传播(backpropogation)。

记第 \(n\) 项数据 \(x^n\) 在神经网络中，训练得到的预测值 \(y^n\) 与实际值 \(\hat{y}^n\) 之差为 \(C^n\)，并且记损失 \(L(\theta) = \sum\limits_{n=1}^n C^n(\theta)\)（\(N\) 项数据的误差和）。因此，对其中的一项参数 \(w\) 求偏微分就是 \(\dfrac{\partial L(\theta)}{\partial w} = \sum\limits_{n=1}^N \dfrac{\partial C^n(\theta)}{\partial w}\)，这样我们将求梯度的问题从对损失 \(L\) 求偏导转换为对每个数据对应的误差 \(C^n\) 求偏导了。

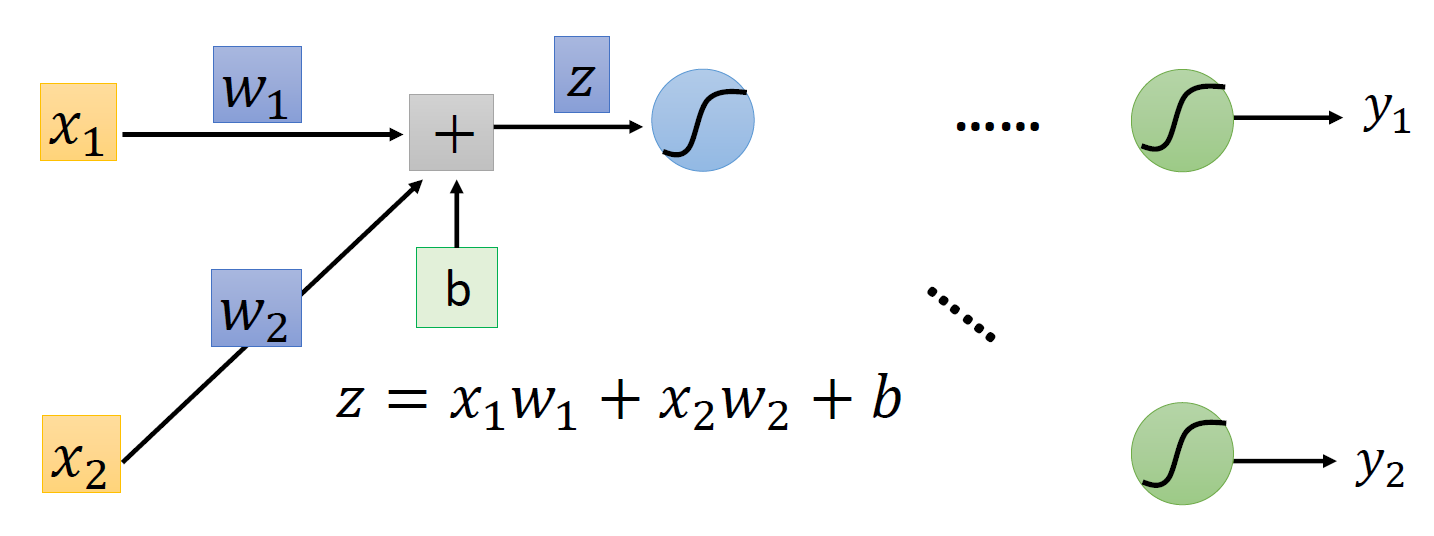
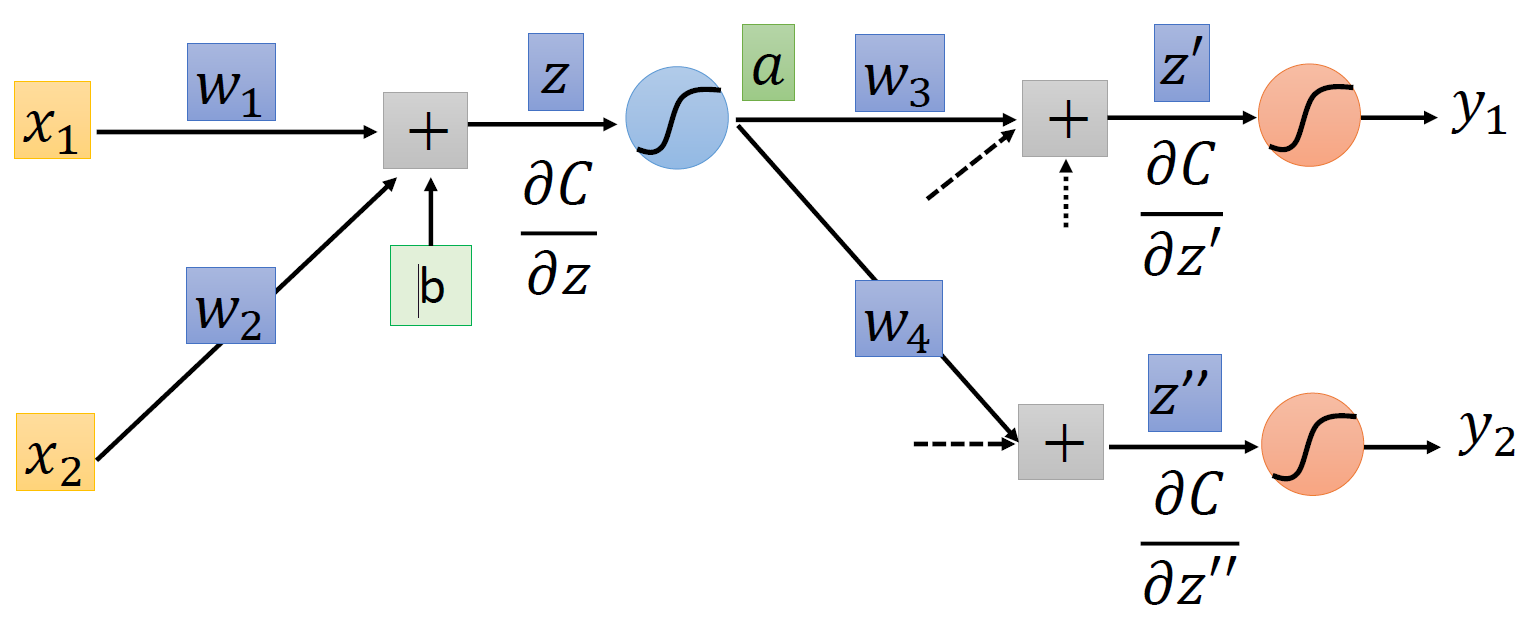
现在考虑如何计算 \(\dfrac{\partial C}{\partial w}\)——根据链式法则，我们可以将其转化为 \(\dfrac{\partial z}{\partial w} \dfrac{\partial C}{\partial z}\)。其中这个 \(z\) 是通过数据输入、权重和偏移计算得到的，如下图所示（简化版本）：

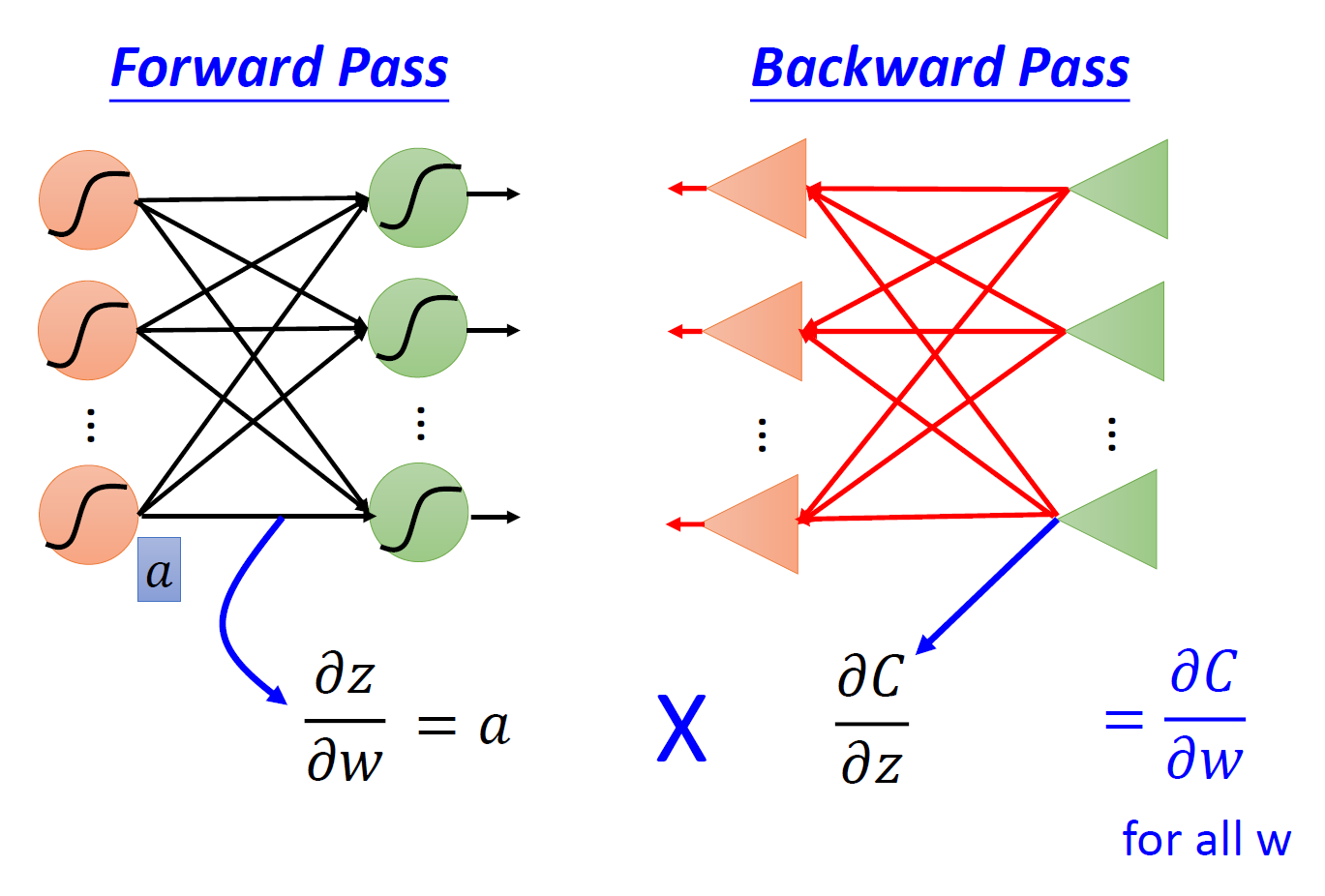
现在计算就被分为两部分了，这两部分同时也是反向传播的组成部分：

• 前递(forward pass)：对所有的参数，计算 \(\dfrac{\partial z}{\partial w}\)
• 后递(backward pass)：对所有的激活函数输入值 \(z\)，计算 \(\dfrac{\partial C}{\partial z}\)

其中前递的计算相当简单：\(\dfrac{\partial z}{\partial w}\) 的值就是与权重相关联的输入数据，因此在训练的过程中，我们顺手就可以将这些值个计算出来。拿上图的例子来说，\(\dfrac{\partial z}{\partial w_1} = x_1, \dfrac{\partial z}{\partial w_2} = x_2\)。

例子

对于更多次的训练，道理也是一样简单。

难点在于计算后递，乍看上去好像无从下手。事实上，后递的计算又一次用到了链式法则：\(\dfrac{\partial C}{\partial z} = \dfrac{\partial a}{\partial z} \dfrac{\partial C}{\partial a}\)，其中 \(a = \sigma(z)\)（sigmoid 函数）。

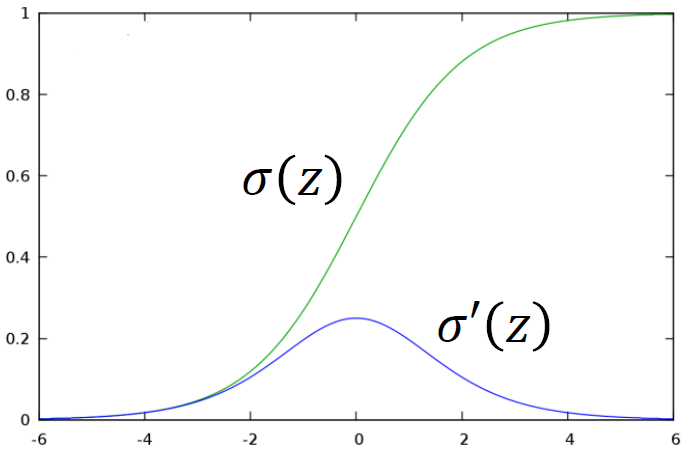
• \(\dfrac{\partial a}{\partial z} = \sigma'(z)\)，因为我们知道 \(z\) 的值（前面的计算中已经算过了），所以 \(\sigma'(z)\) 就是一个常量

  sigmoid 函数及其导函数的图像

  

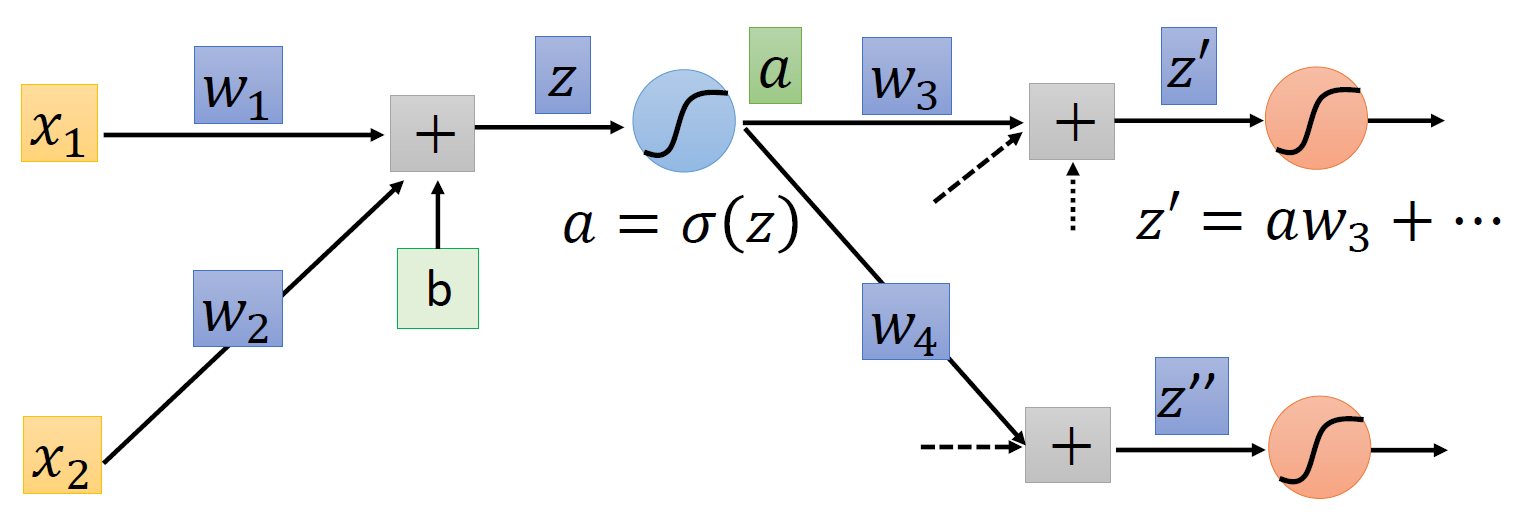
• \(\dfrac{\partial C}{\partial a}\)：又又一次用到链式法则，借助下图来理解这个过程：

  

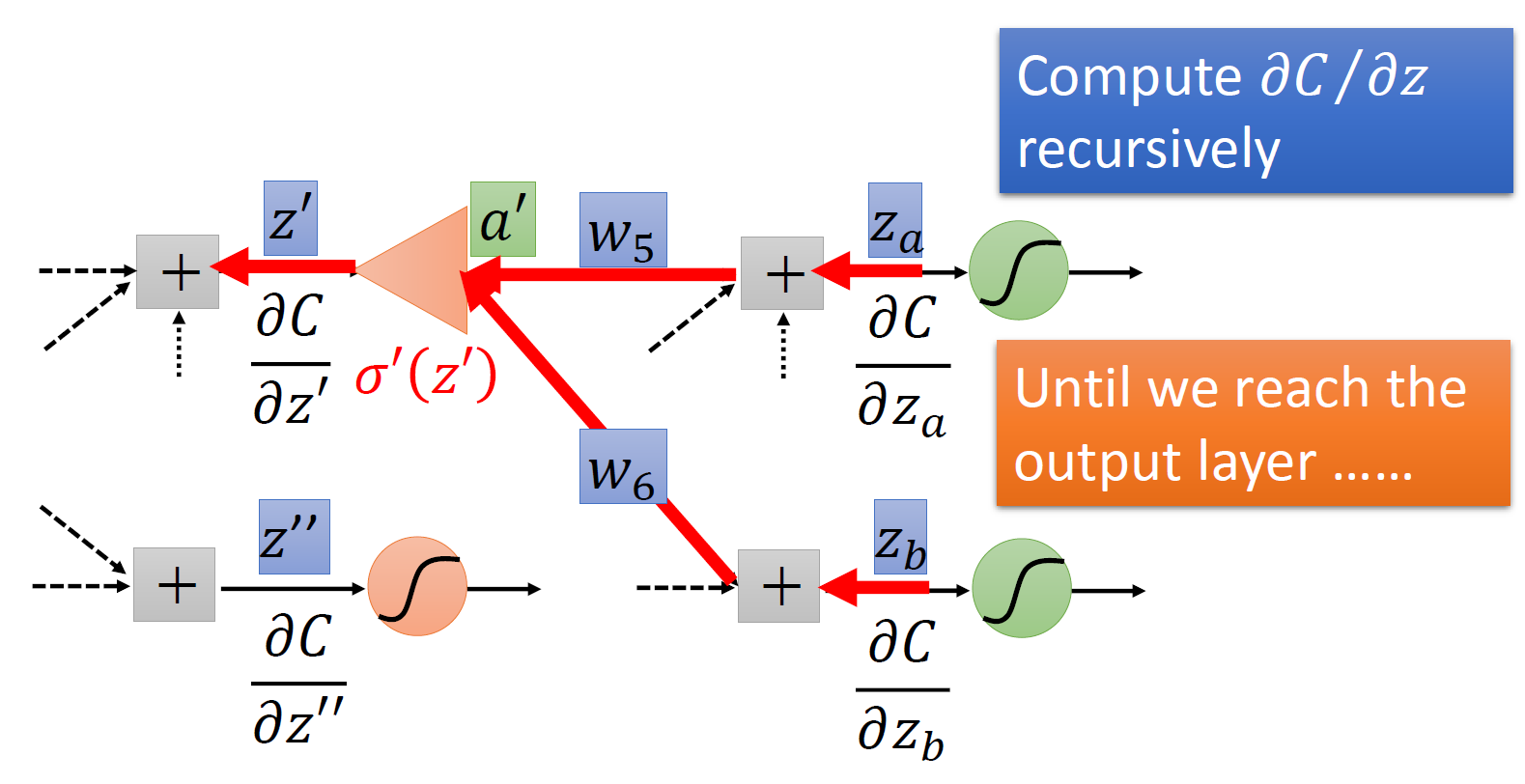
  可以看到，\(a\) 的值会影响到 \(z', z''\)，因此 \(\dfrac{\partial C}{\partial a} = \dfrac{\partial z'}{\partial a} \dfrac{\partial C}{\partial z'} + \dfrac{\partial z''}{\partial a} \dfrac{\partial C}{\partial z''}\)。其中 \(\dfrac{\partial z'}{\partial a}, \dfrac{\partial z''}{\partial a}\) 的值很容易计算，就是对应的权重 \(w_3, w_4\)，而 \(\dfrac{\partial C}{\partial z'}, \dfrac{\partial C}{\partial z''}\) 的值我们先暂时假设它们是已知量

总结一下：\(\dfrac{\partial C}{\partial z} = \sigma'(z) \Big[w_3 \dfrac{\partial C}{\partial z'} + w_4 \dfrac{\partial C}{\partial z''}\Big]\)。最后有待求解的就是刚才假设已知的那两个偏导数，这里我们分为两种情况讨论：

1. 如果它们位于最后一次的训练过程中（即在输出层中），那么：

   
   \[ \dfrac{\partial C}{\partial z'} = \dfrac{\partial y_1}{\partial z'} \dfrac{\partial C}{\partial y_1} \quad \dfrac{\partial C}{\partial z''} = \dfrac{\partial y_2}{\partial z''} \dfrac{\partial C}{\partial y_2} \]

   这些量都是相当好计算的，所以结果自然就求出来了

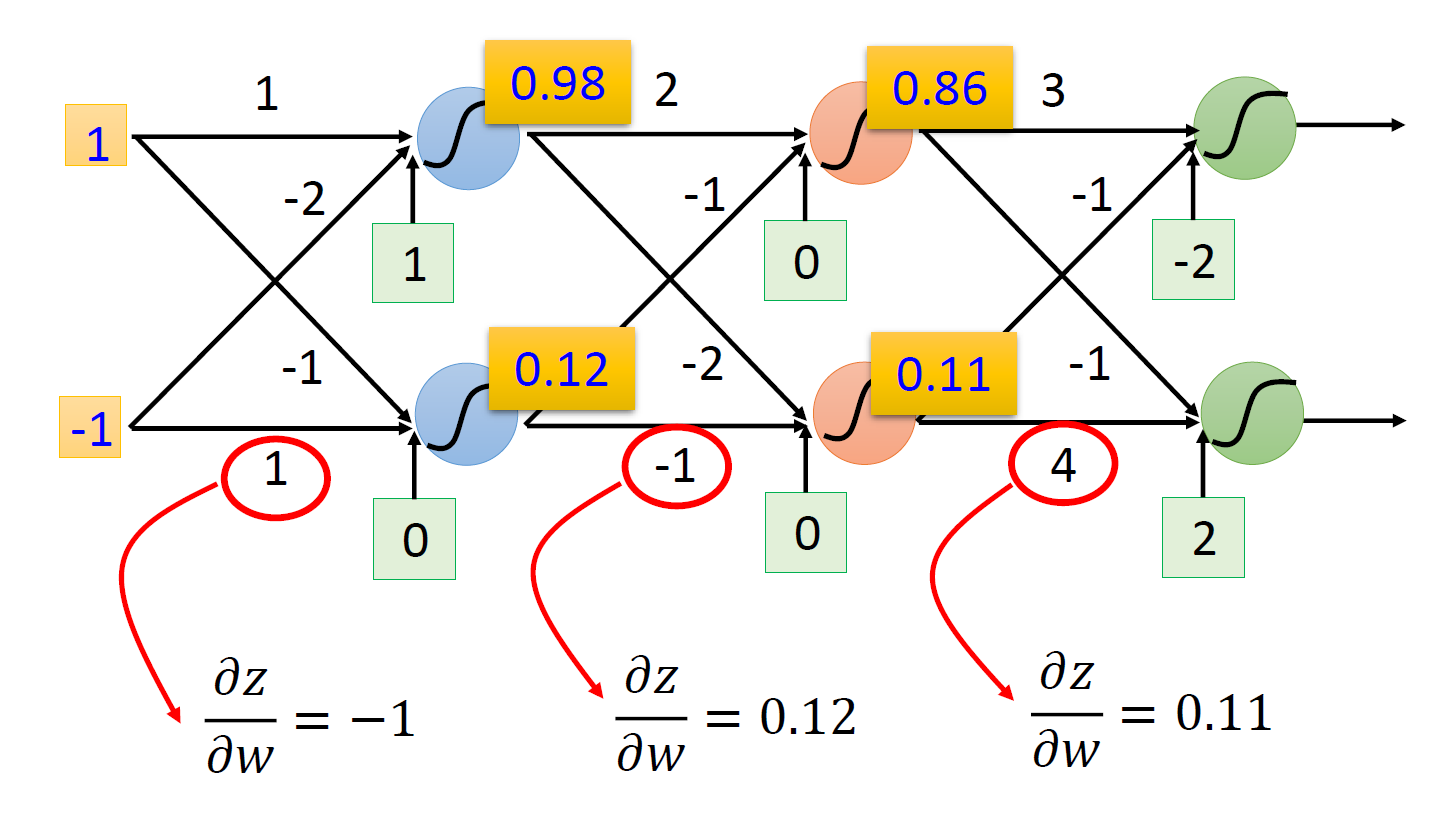
2. 如果是在中间的训练过程中，那计算思路如下图所示：

   

   以 \(z'\) 为例稍作解释：要求 \(\dfrac{\partial C}{\partial z'}\)，可以像求 \(\dfrac{\partial C}{\partial z}\) 那样继续借助后面的计算值 \(z_a, z_b\) 求解，连计算思路都是一样的。如此往复计算，直到计算到达输出层（即第一种情况时），我们可以依次往前计算前面所有的这些偏导数了！

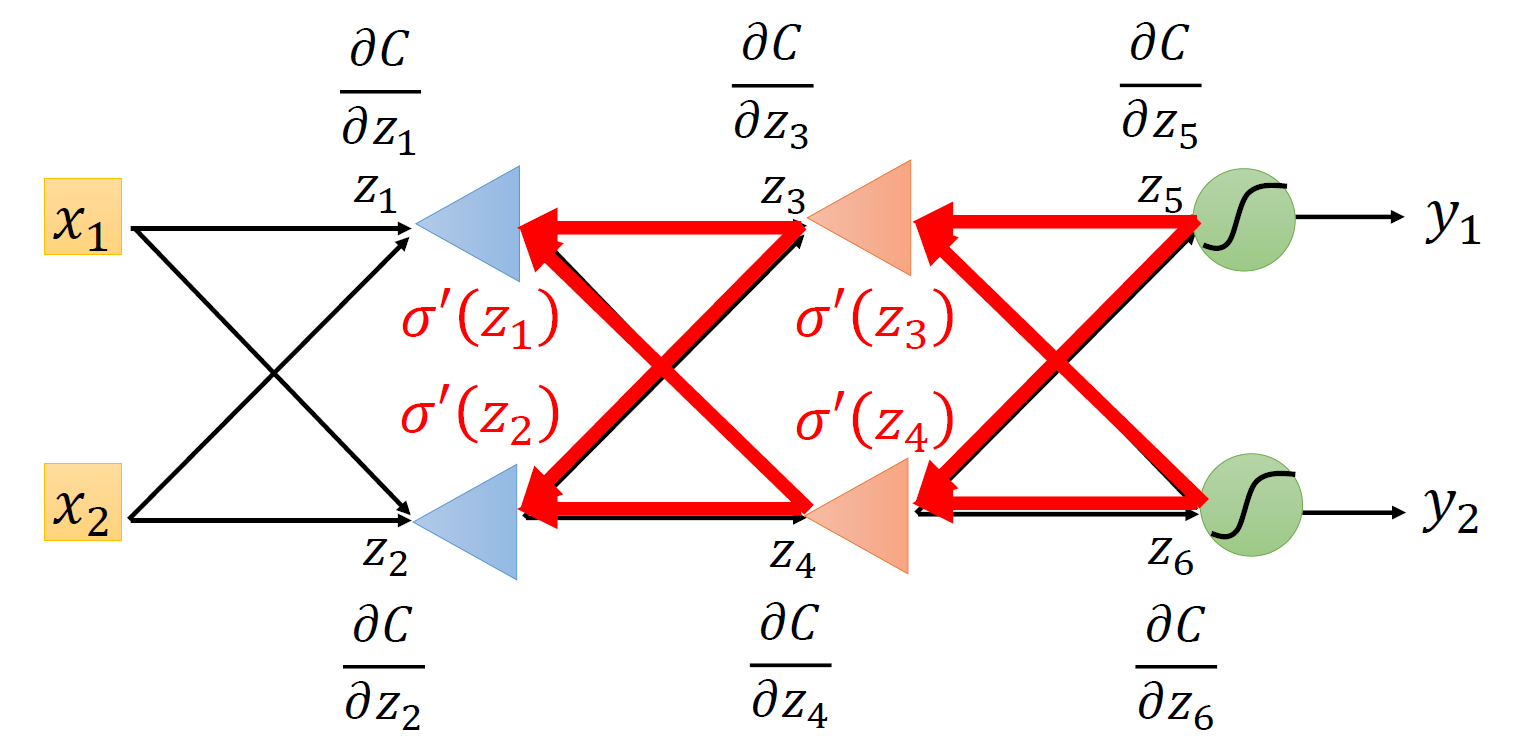
事实上，在计算形如 \(\dfrac{\partial C}{\partial z}\) 这类偏导数时，我们可以直接通过输出值 \(y_1, y_2, \dots\) 按反方向计算，这也就是该算法名称的由来。

总结

Critical Points⚓︎

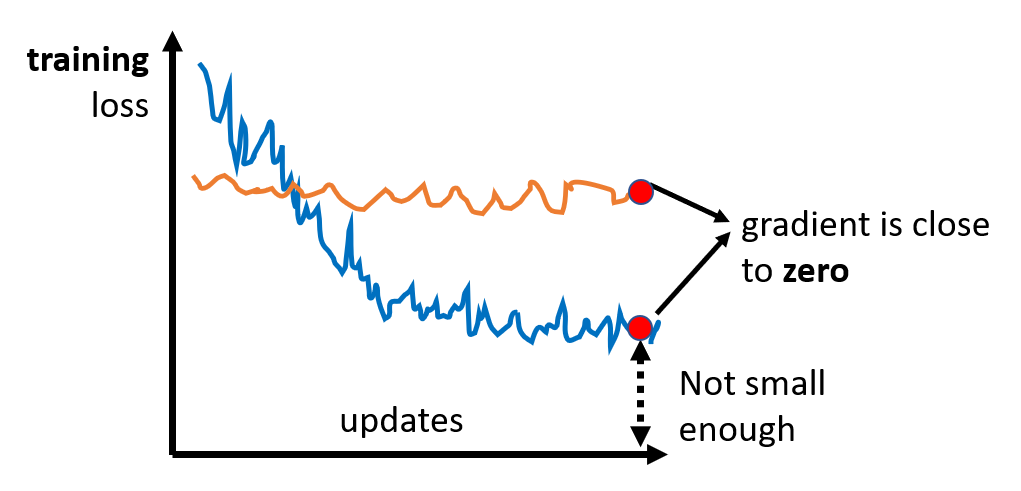
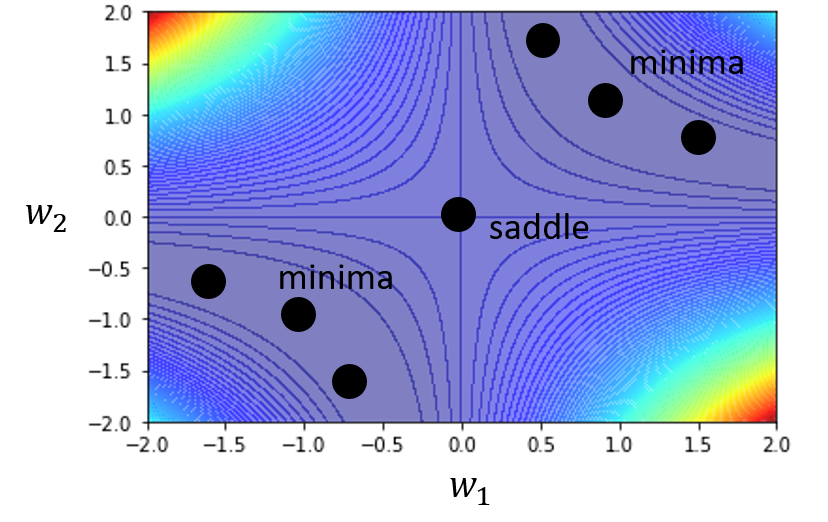
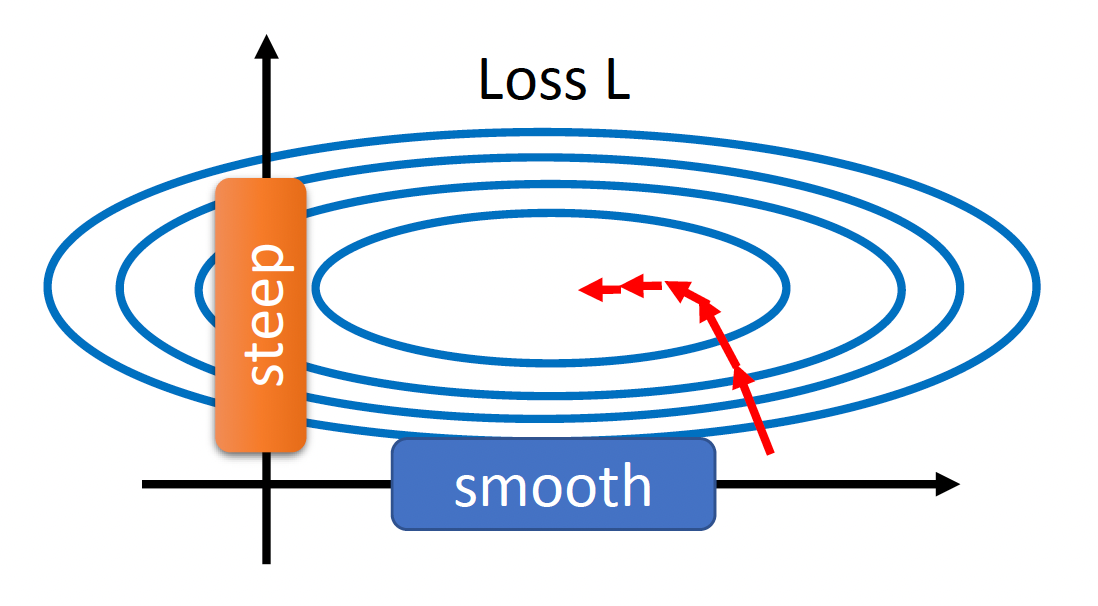
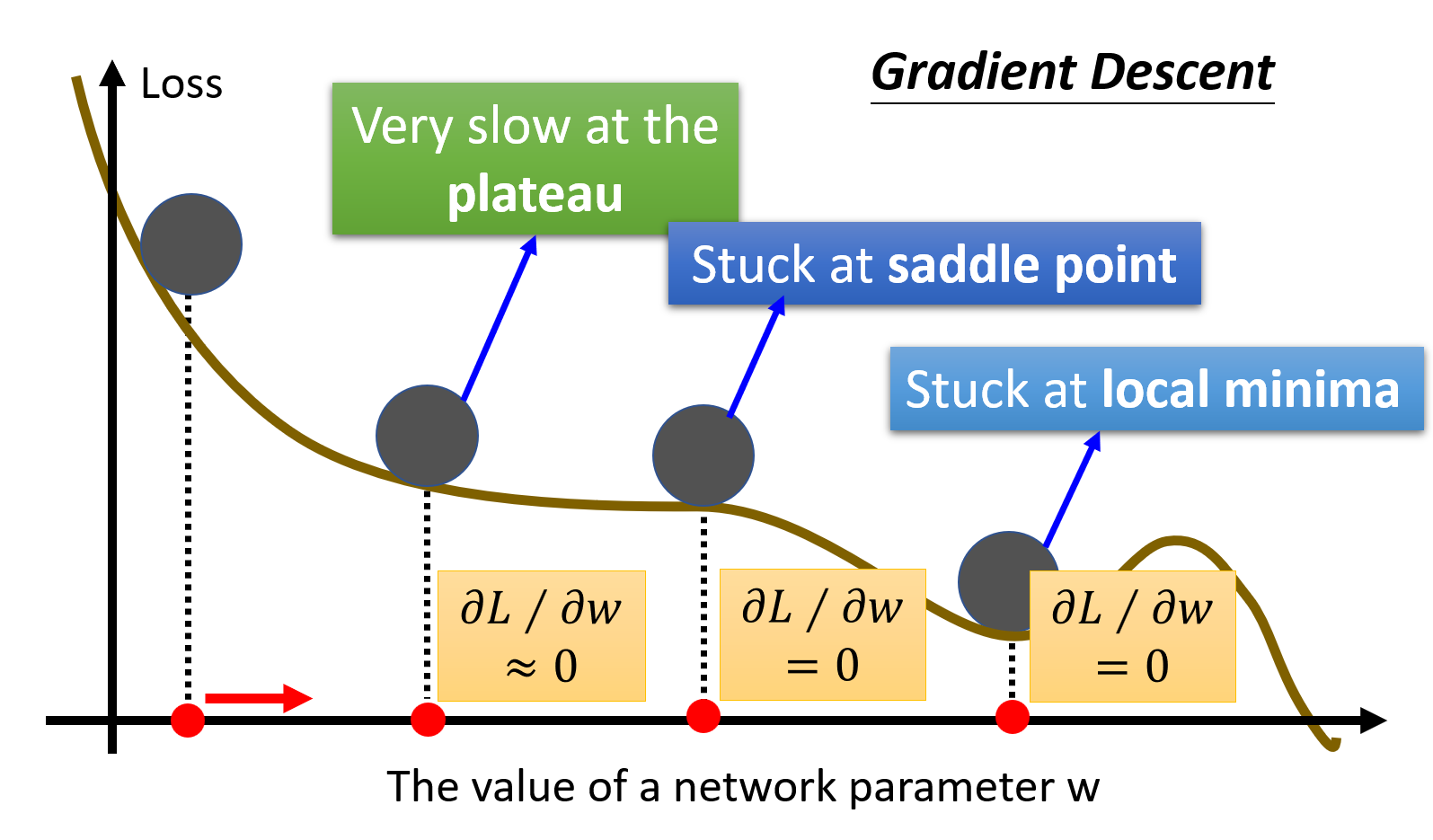
在训练模型的时候，我们可能会遇到模型的损失无法进一步减小，也就是无法继续优化的情况。以梯度下降法为例，当梯度接近 0的时候就会出现这种情况，如下图所示：

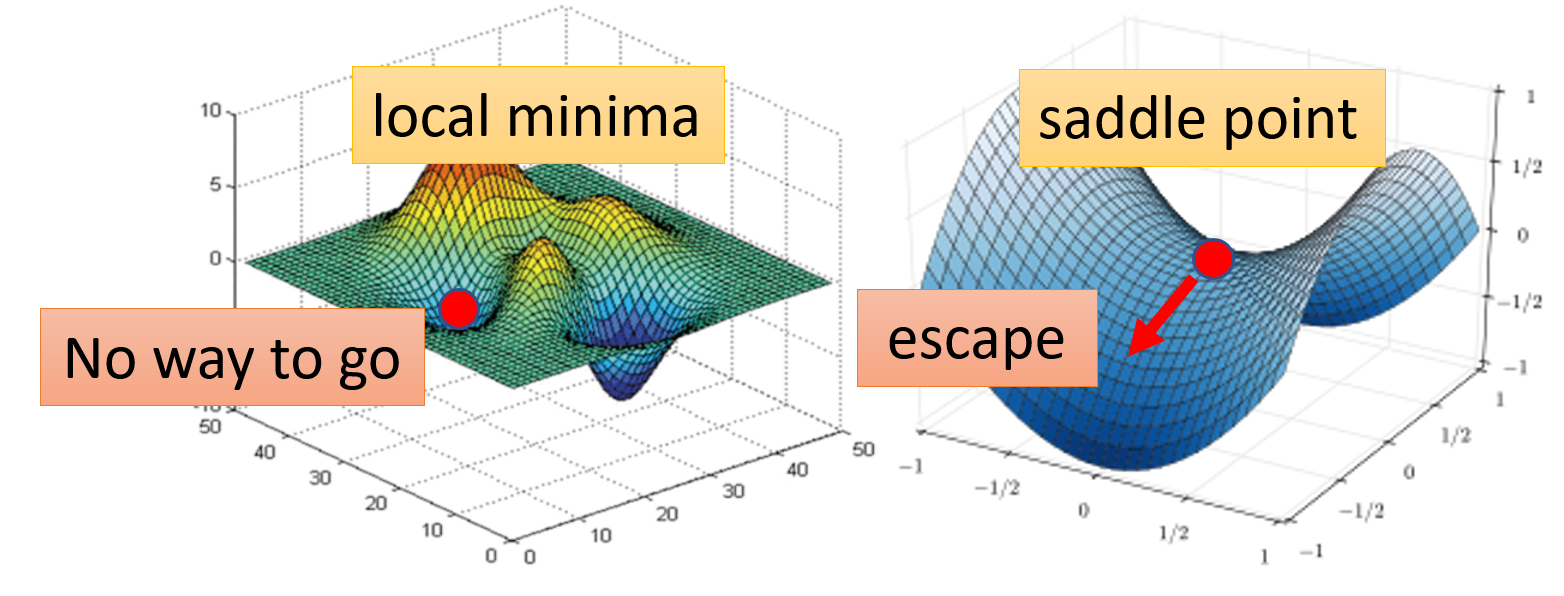
当梯度为 0 时，除了前面介绍过的局部最小(local minima) 的情况，还有一种情况是位于鞍点(saddle point)：在某些方向上它是局部最小值，但是在另外的方向上它是局部最大值，因而可以逃脱局部最小值的困境。从形状看像一个马鞍，因而得名。我们将这两种情况统称为关键点(critical point)。

那么现在的问题是：已知梯度为 0，我们该如何区分这属于哪一类关键点呢？这里就要用到一些微积分和线性代数的知识了。

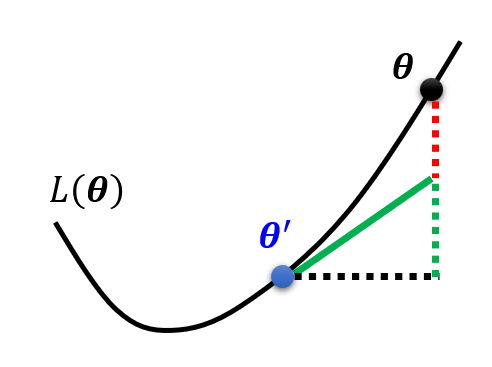
首先要利用泰勒级数(Taylor Series) 进行近似表示。假设某个参数下的损失为 \(L(\bm{\theta})\)，并且已知 \(\bm{\theta}'\) 附近很小的一个范围内的有一个 \(\bm{\theta}\)，那么 \(L(\bm{\theta})\) 可以被表示为：

其中：

• 梯度 \(\bm{g} = \nabla L(\bm{\theta}')\) 是一个向量，向量内元素 \(\bm{g}_i = \dfrac{\partial L(\bm{\theta}')}{\partial \bm{\theta}_i}\)
• 黑塞矩阵(Hessian matrix) \(H\) 的元素为 \(H_{ij} = \dfrac{\partial^2}{\partial \bm{\theta}_i \partial \bm{\theta}_j} L(\bm{\theta}')\)

如果遇到关键点的话，\(\bm{g} = 0\)，那么中间项就可以消掉，只剩下：

我们正是通过最后一项来判断关键点的类型。为了便于后续讲述，先令 \(\bm{v}^T H \bm{v} = (\bm{\theta} - \bm{\theta}')^T H (\bm{\theta} - \bm{\theta}')\)。对于所有的 \(\bm{v}\)，如果：

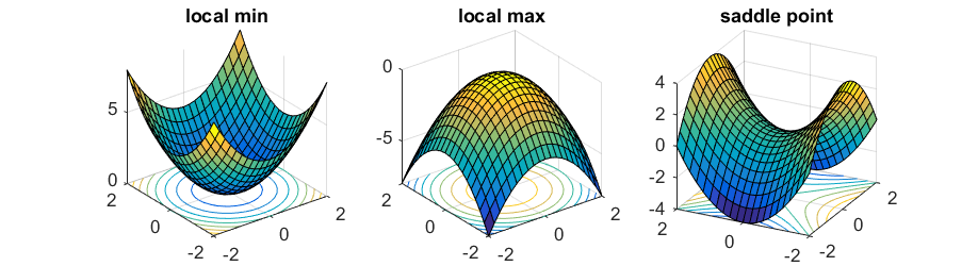
• \(\bm{v}^T H \bm{v} > 0\)，那么对于在 \(\bm{\theta}'\) 附近的 \(\bm{\theta}\)，满足 \(L(\bm{\theta}) > L(\bm{\theta}')\)，因此这是一个局部最小点
  • 等价表述：当 \(H\) 为正定(positive definite) 矩阵，即所有特征值 (eigen values) 均为正数时，表明到达了局部最小点
• \(\bm{v}^T H \bm{v} < 0\)，那么对于在 \(\bm{\theta}'\) 附近的 \(\bm{\theta}\)，满足 \(L(\bm{\theta}) < L(\bm{\theta}')\)，因此这是一个局部最大点
  • 等价表述：当 \(H\) 为负定(negative definite) 矩阵，即所有特征值均为负数时，表明到达了局部最大点
• 有时 \(\bm{v}^T H \bm{v} > 0\)，而有时 \(\bm{v}^T H \bm{v} < 0\)，那么这是一个鞍点
  • 等价表述：当 \(H\) 的特征值有正有负时，表明到达了鞍点

例子

假设有一个很烂的模型 \(y = w_1 w_2 x\)，且已知训练数据 \((x, \hat{y}) = (1, 1)\)（仅 1 组）。那么该模型的误差曲面 (error surface) 如下所示（图上已标出局部最小点和鞍点）：

用 MSE 计算损失为：\(L = (\hat{y} - w_1 w_2 x)^2 = (1 - w_1 w_2)^2\)。然后计算每个参数关于损失的一阶和二阶微分，分别作为梯度和黑塞矩阵的元素：

当 \(w_1 = w_2 = 0\) 时，发现梯度为 0，那么该点就是关键点。而且此时黑塞矩阵 \(H = \begin{bmatrix} 0 & -2 \\ -2 & 0\end{bmatrix}\)，特征值 \(\lambda_1 = 2, \lambda_2 = -2\)，因此可以判定该点为鞍点。

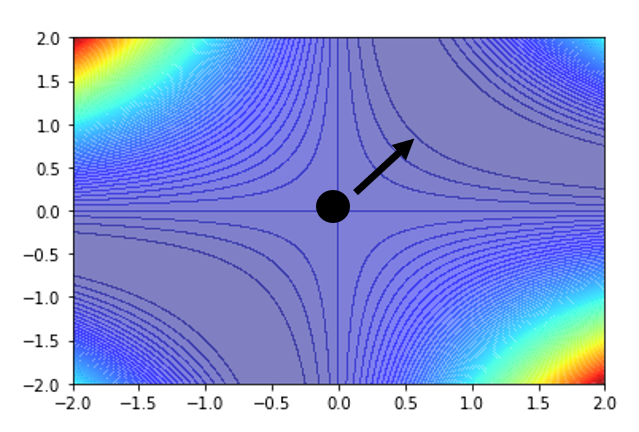
对于鞍点而言，黑塞矩阵除了能够用于判断外，还能为我们指示离开鞍点，即更新参数的方向。现在假设 \(\bm{u}\) 是 \(H\) 的一个特征向量，\(\lambda\) 是 \(u\) 的特征值，那么：

因此，如果 \(\lambda < 0\) 的话，那么 \(\bm{u}^T H \bm{u} < 0\)。回到前面关于损失的泰勒展开式 \(L(\bm{\theta}) = L(\bm{\theta}') + \dfrac{1}{2} (\bm{\theta} - \bm{\theta}')^T H (\bm{\theta} - \bm{\theta}')\)，令 \(\bm{u} = \bm{\theta} - \bm{\theta}'\)，那么 \(\bm{\theta} = \bm{\theta}' + \bm{u}\)。由于此时 \(L(\bm{\theta}) < L(\bm{\theta}')\)，即 \(\bm{\theta}'\) 位于局部最大点，那么从该点沿 \(\bm{u}\) 的方向走的话，损失就会变小，从而离开局部最大点。总之，通过黑塞矩阵的特征向量，我们总能设法离开鞍点。

例子

接着前面的例子，第二个特征值为 \(\lambda_2 = -2\)，对应特征向量 \(\bm{u} = \begin{bmatrix}1 \\ 1\end{bmatrix}\)。只要沿着 \(u\) 的方向更新参数，损失就会减小，如下面的误差曲面所示：

实践上，一般并不会实现这种方法，因为计算二次微分、特征值和特征向量等等运算太过复杂，效率不高。

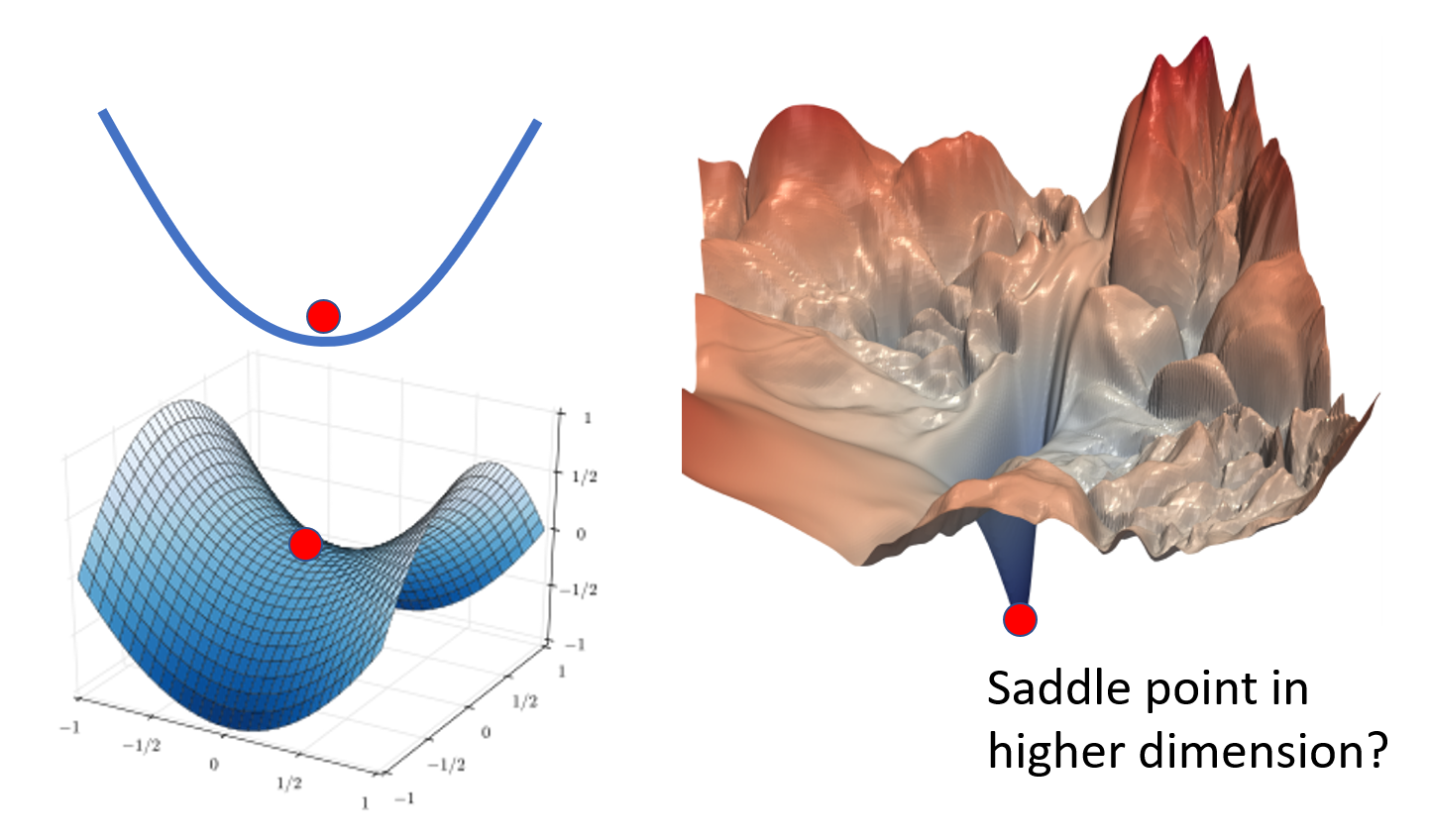
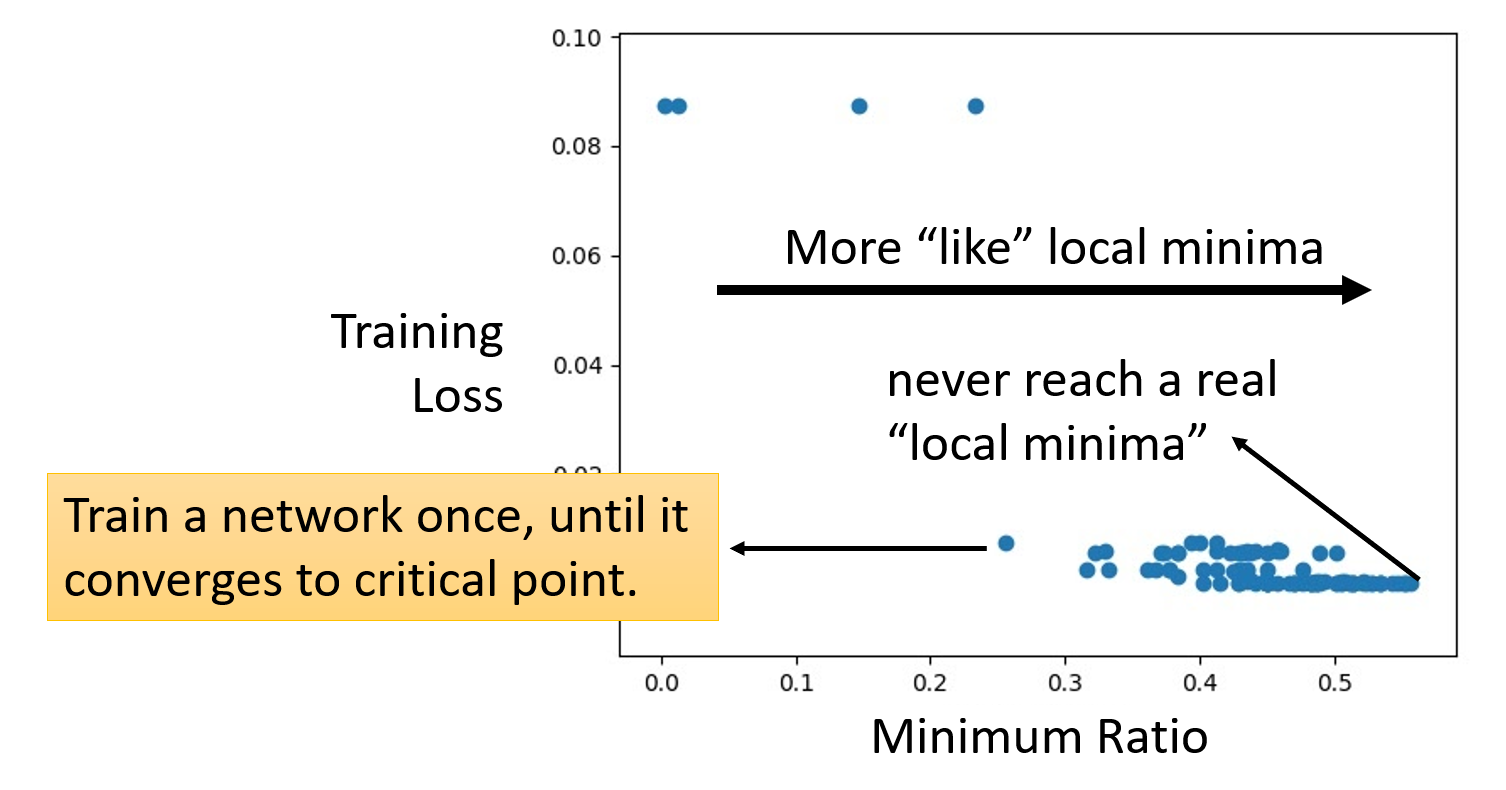
那么鞍点和局部最小点这两种关键点，哪个更为常见呢？

可以看到，二维平面上的局部最小点，可能到三维乃至更高位的空间内就是一个鞍点，因为更多的维数意味着更多的逃离局部最小的可能。所以当参数足够多的时候，鞍点的数量可能相对更多一些。

事实上，上述理论有实践经验的支撑，如下图所示：

其中横轴表示最小值比率(minimum ratio)，即局部最小点在所有关键点中的占比，计算公式为：

可以看到，当我们通过不断的训练将损失降得尽可能低时，最小值比率维持在 0.5-0.6 之间，也就是说始终没法达到真正的局部最小值（最小值比率 = 1），因此局部最小点在具体实现中属于罕见的情况。

Batches⚓︎

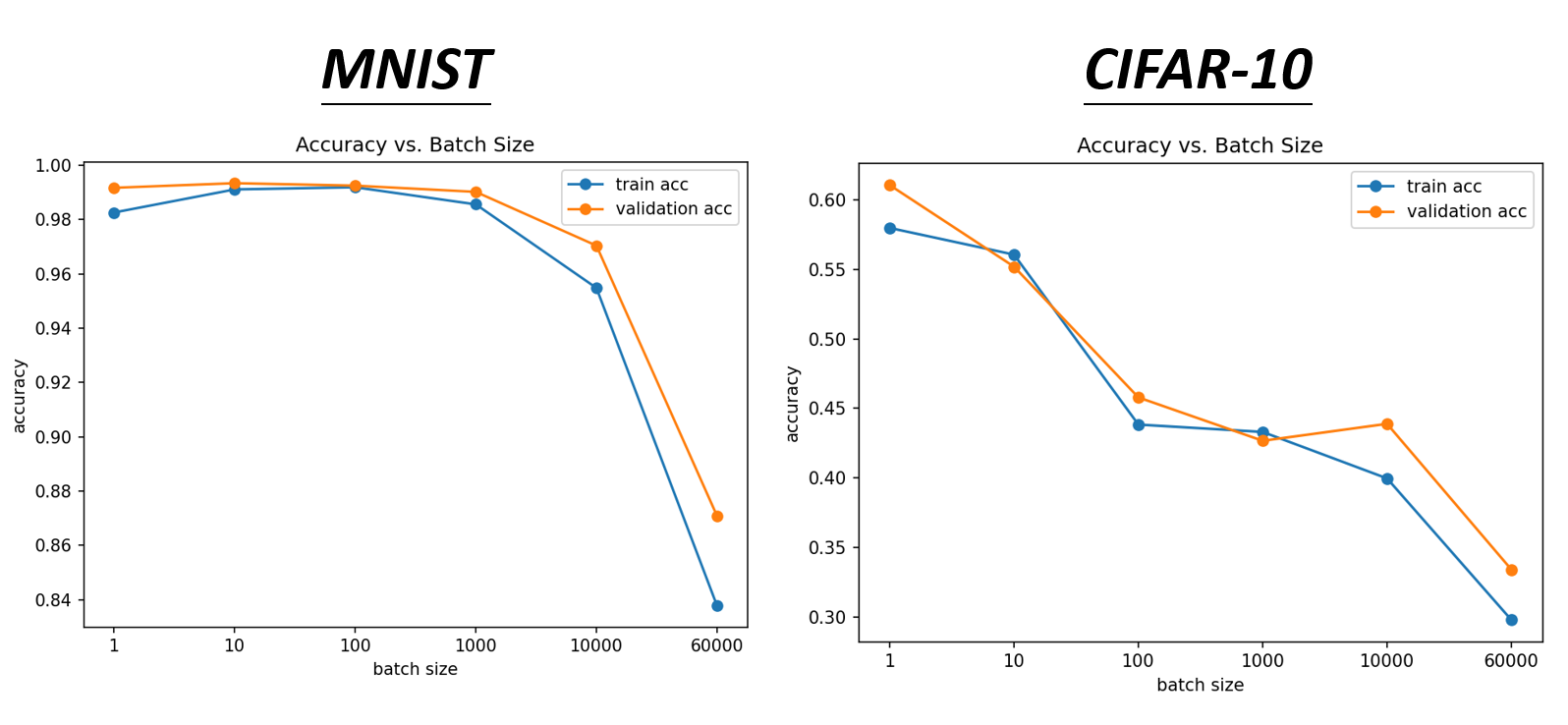
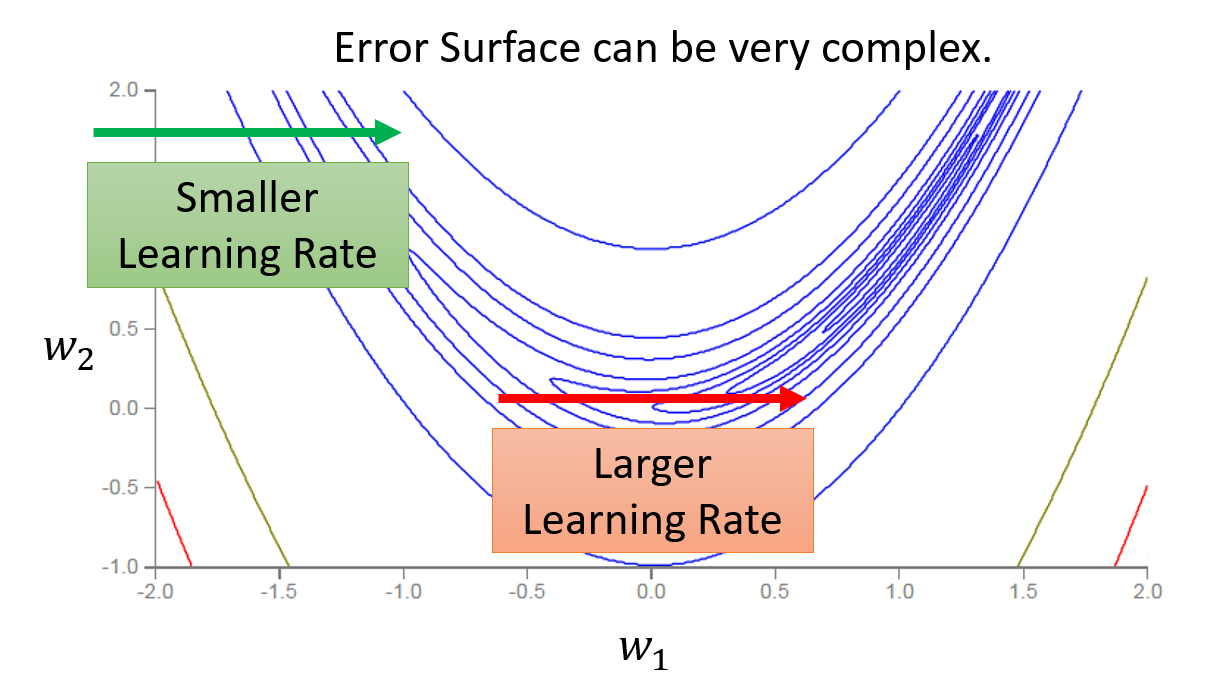
前面提到过，对于参数量很大的模型，会分批(batch) 使用梯度下降法来更新参数，而不是一次性对所有参数求梯度。下面就通过对比更新小批量和大批量参数的效果，来说明为何需要分批更新。

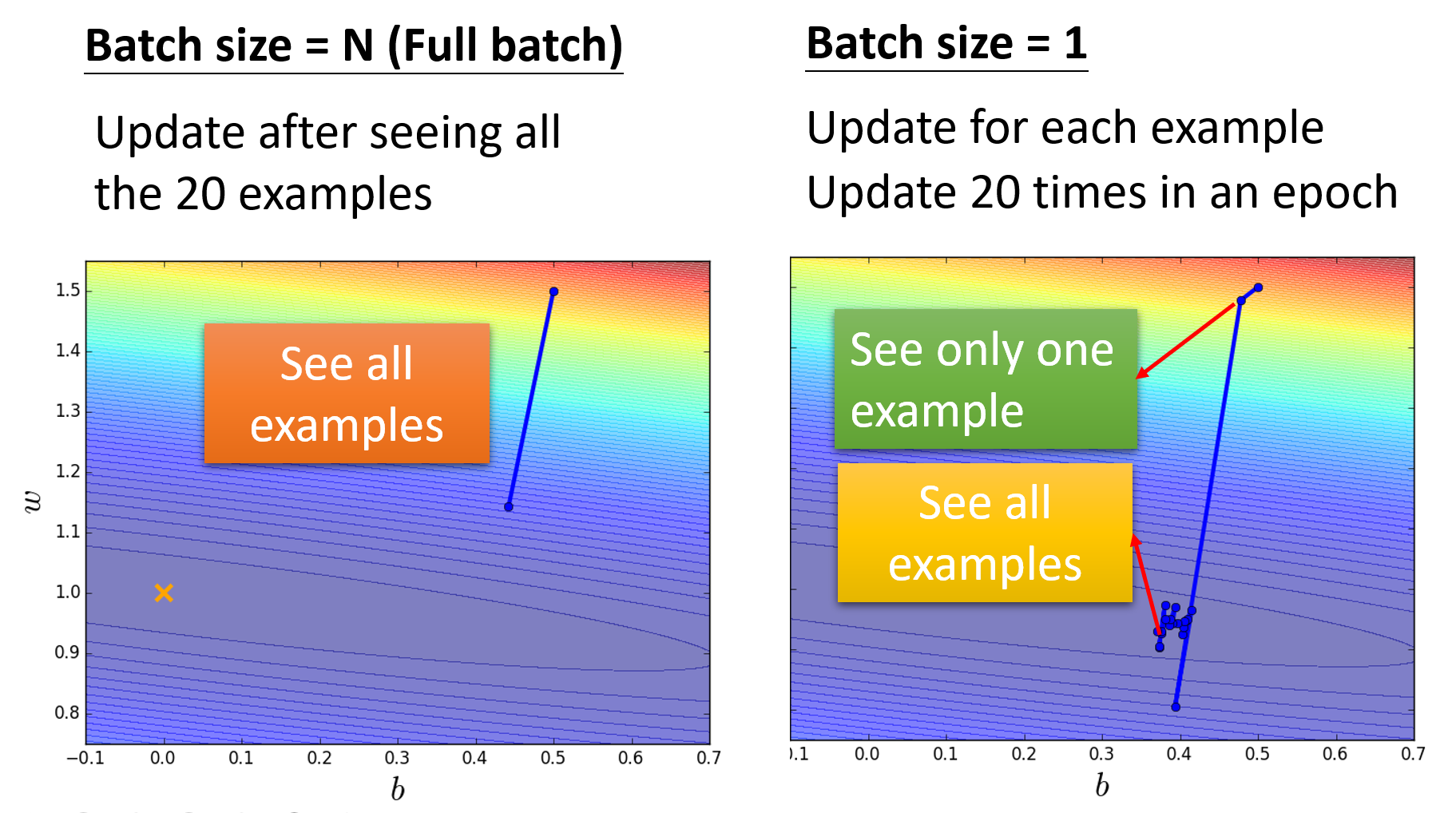
假如模型有 N = 20 的参数，现提供两种（极端的）大小：大批的大小为 N，小批的大小为 1。下面通过误差曲面来分析两者的优化效果：

• 大批量：更新时间长（要处理 20 个参数），但是优化效果很好（powerful）
• 小批量：更新时间很短（1 次只更新 1 个参数），但是有很多噪点（noisy）

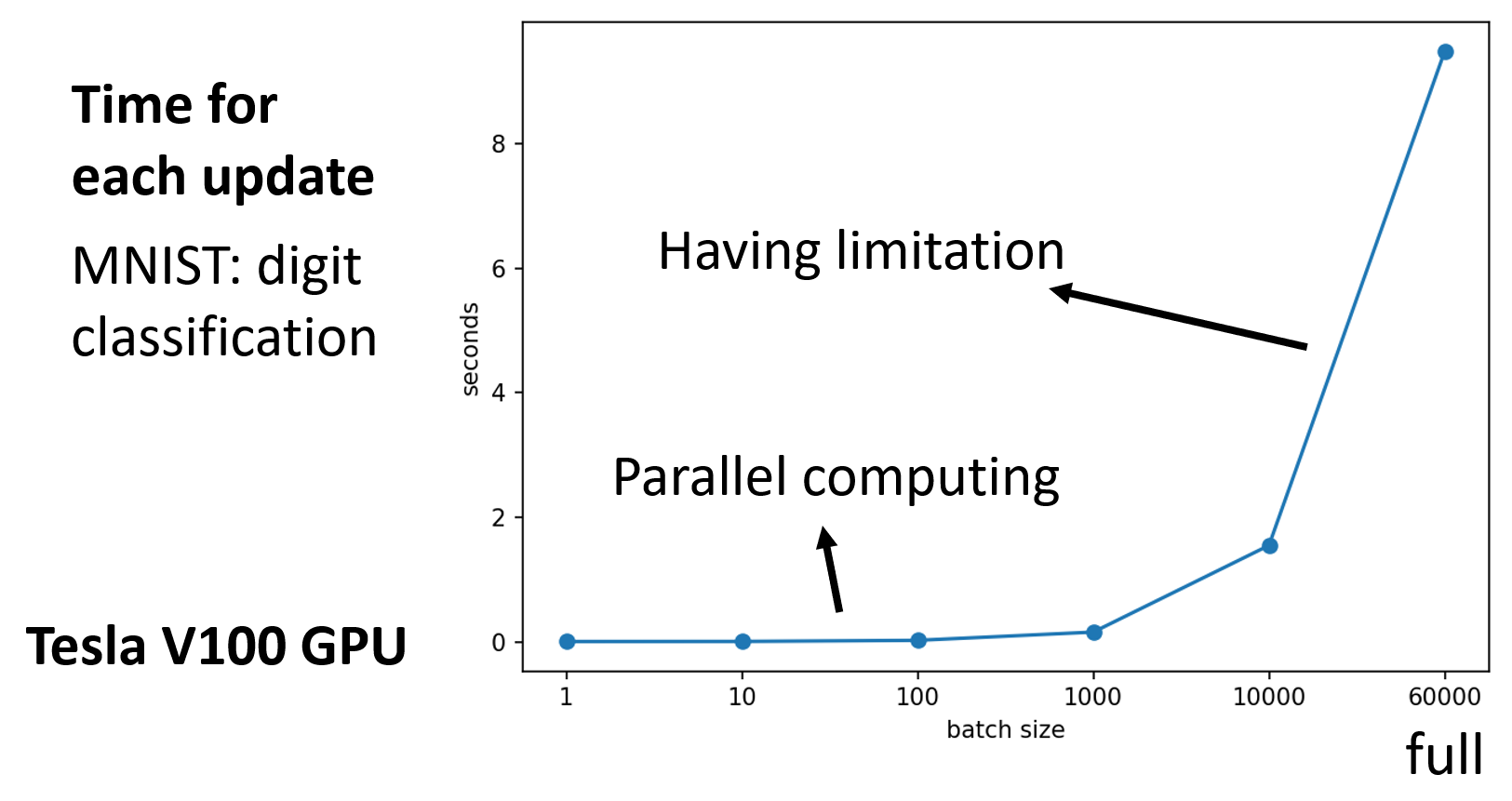
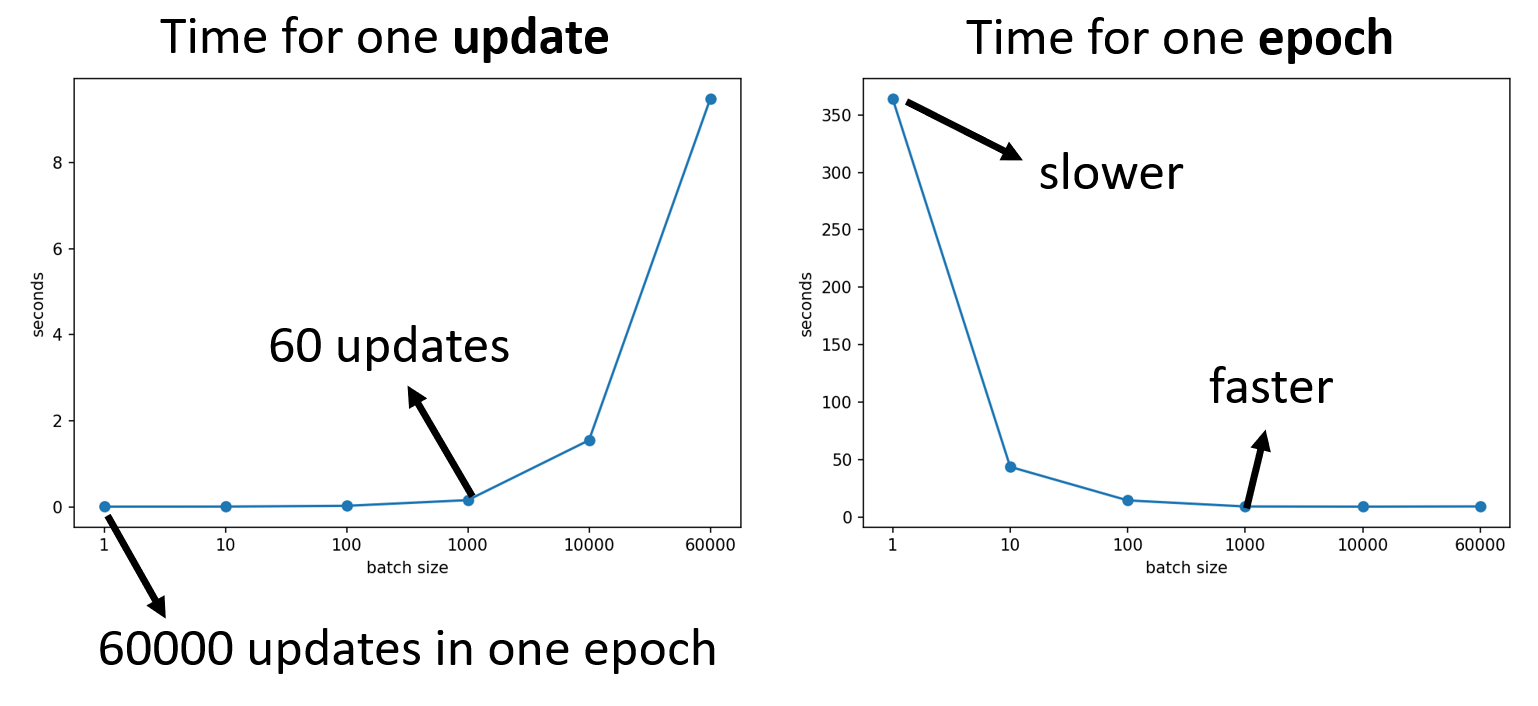
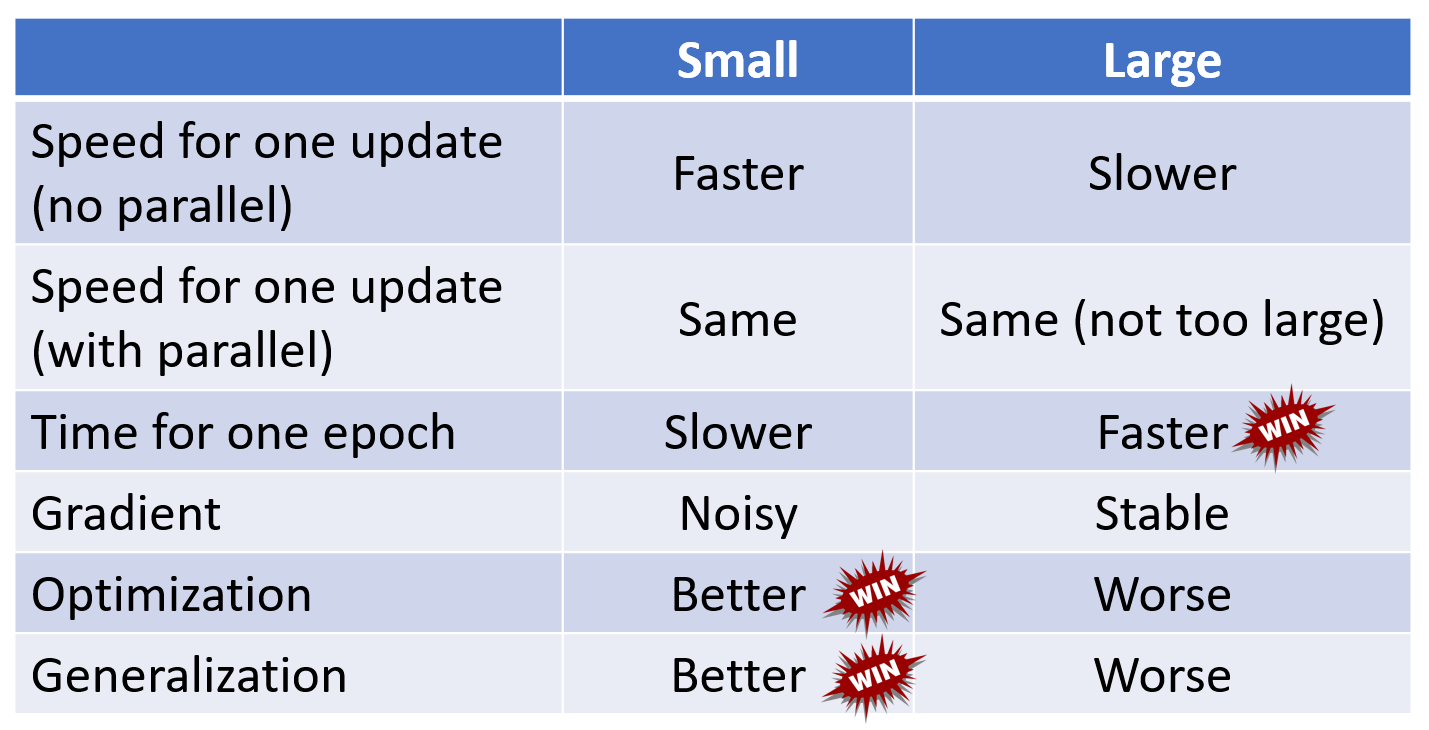
因此直接看貌似看不出两者有哪个能占据很大优势。其实上面只是做了理论层面的分析，实际上在机器学习中常常用到 GPU，而 GPU 的一大优势在于支持并行计算，因此我们得重新考虑时间上的估量了：

• 大批量并不意味着需要花更长的时间计算梯度（除非批量太大）

  

• 在一个时期 (epoch) 内，小批量反而需要花费更多的时间

  

尽管小批量在时间上并不占据太大的优势，但是它的强大之处在于能确保训练模型的精度，使模型具备更好的表现。

例子

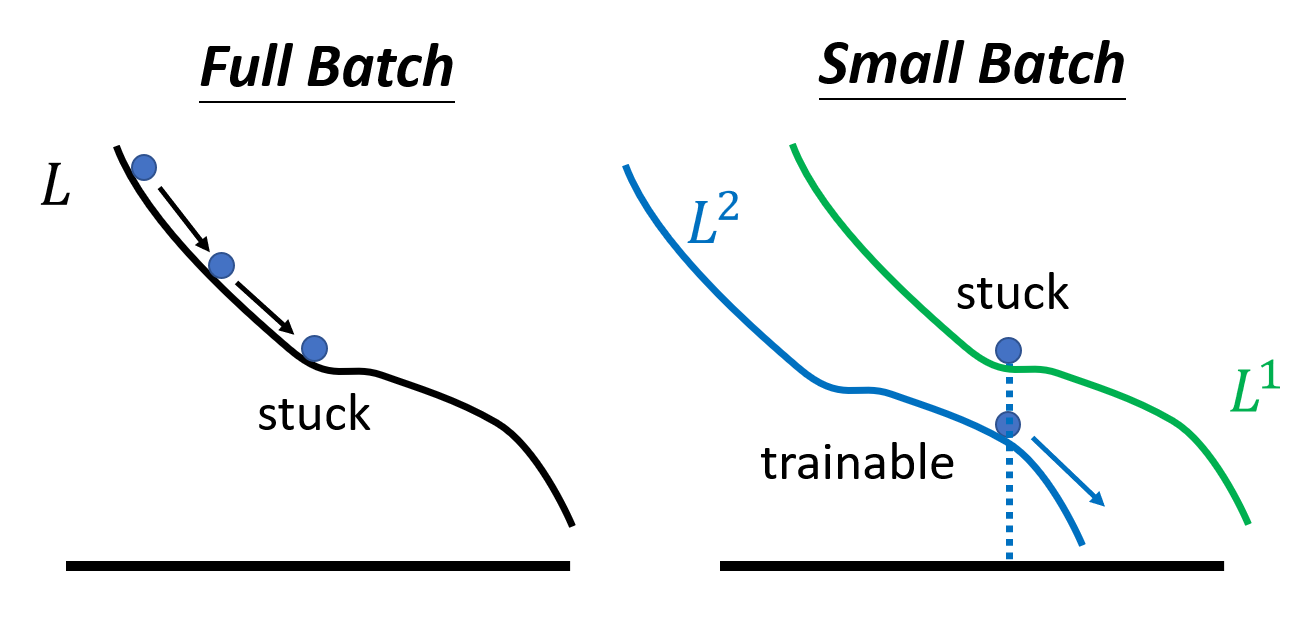
之所以大批量不好，并不是因为模型偏移或过拟合，而是优化上的不足：

• 对于大批量，尤其是全批量，未知参数关于损失的函数通常只有少数几条甚至一条，因此每次更新都顺着几乎既定的路径走。如果遇到了关键点，那么就很容易卡在那里不动了
• 对于小批量，由于每次只更新一小部分，因此会产生不同的损失函数。即使模型在优化的时候卡在某个损失函数上，只需更新一下，就跳到另一个损失函数，从而有很大概率避开了关键点

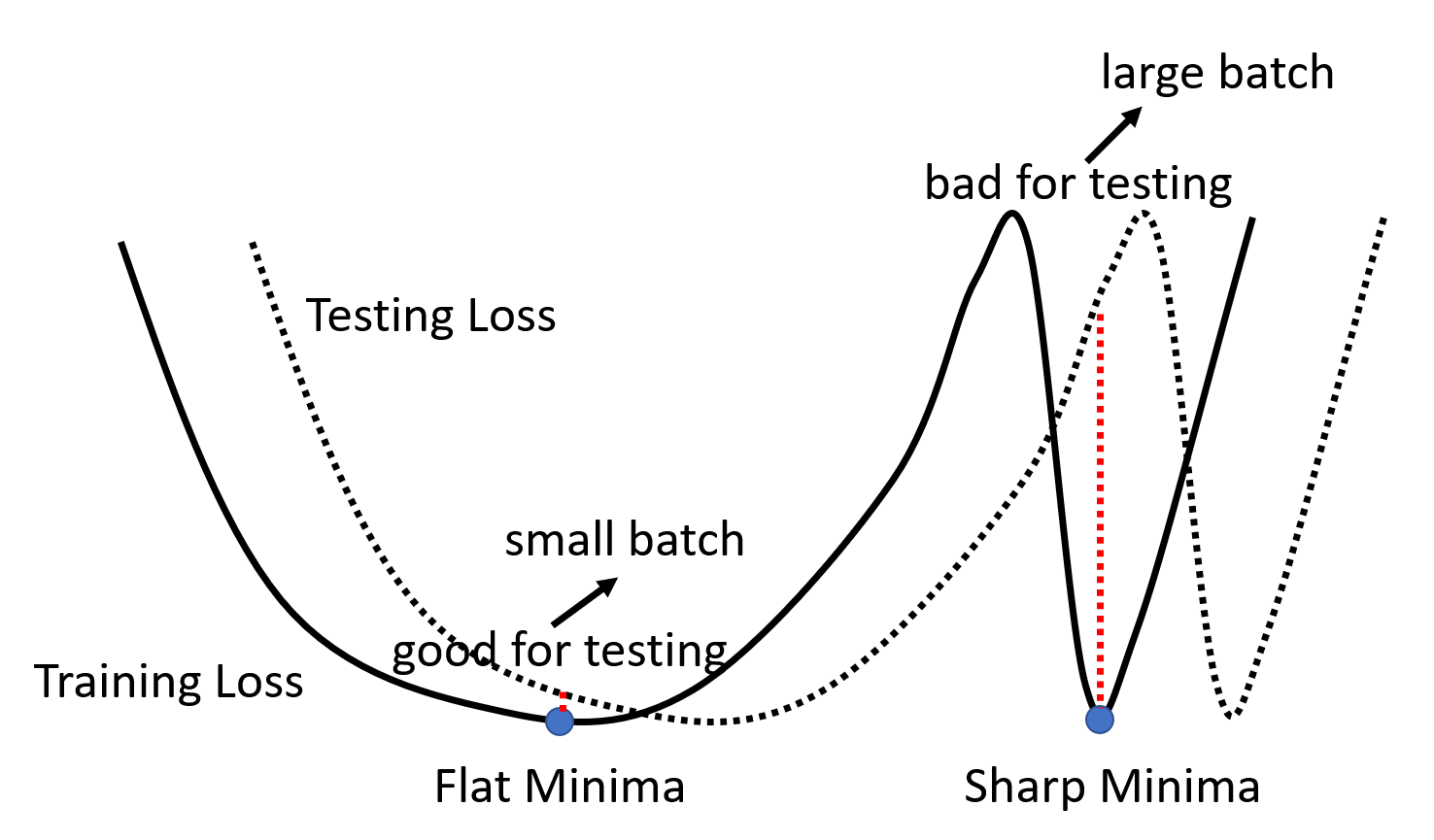
下面从另一个角度解释原因。对于训练数据上的损失函数，不同的局部最小点也有好坏之分，我们会认为狭窄的局部最小点是不利于测试的，而平坦的局部最小点相对而言比较好一些。如下图所示，假如训练数据上和测试数据上的损失函数有些错误匹配 (mismatch)，那么局部最小点的好坏之分就表现得非常明显了：平坦的局部最小点在测试数据上没多大变动，而狭窄的局部最小点在测试数据上的损失就一下子变得很高。对于小批量而言，由于它的更新策略更具灵活性（noisy），因此它很容易跳脱这种狭窄的局部最小点；而对于大批量而言，它的行为有些“循规蹈矩”，因此很容易陷入狭窄的局部最小点而无法逃脱。所以通过小批量优化得到的模型表现会更好。

总结

批量大小是一个超参数(hyperparameter)，我们可以根据需要进行手工调整。

Batch Normalization⚓︎

由于误差曲面过于崎岖对训练带来不小的障碍，因此我们希望改善误差曲面的状况，而本节介绍的批量归一化(batch normalization) 正是其中一种解决方案。在正式介绍前，我们先来看这样一个误差曲面：

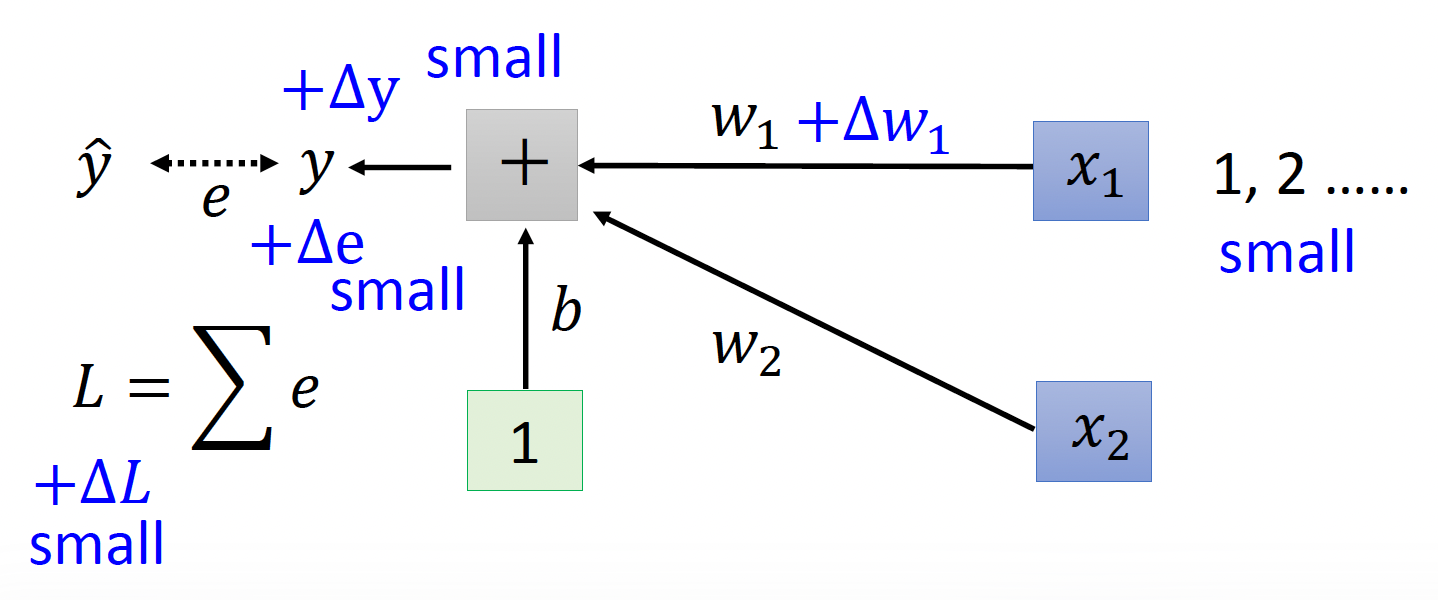
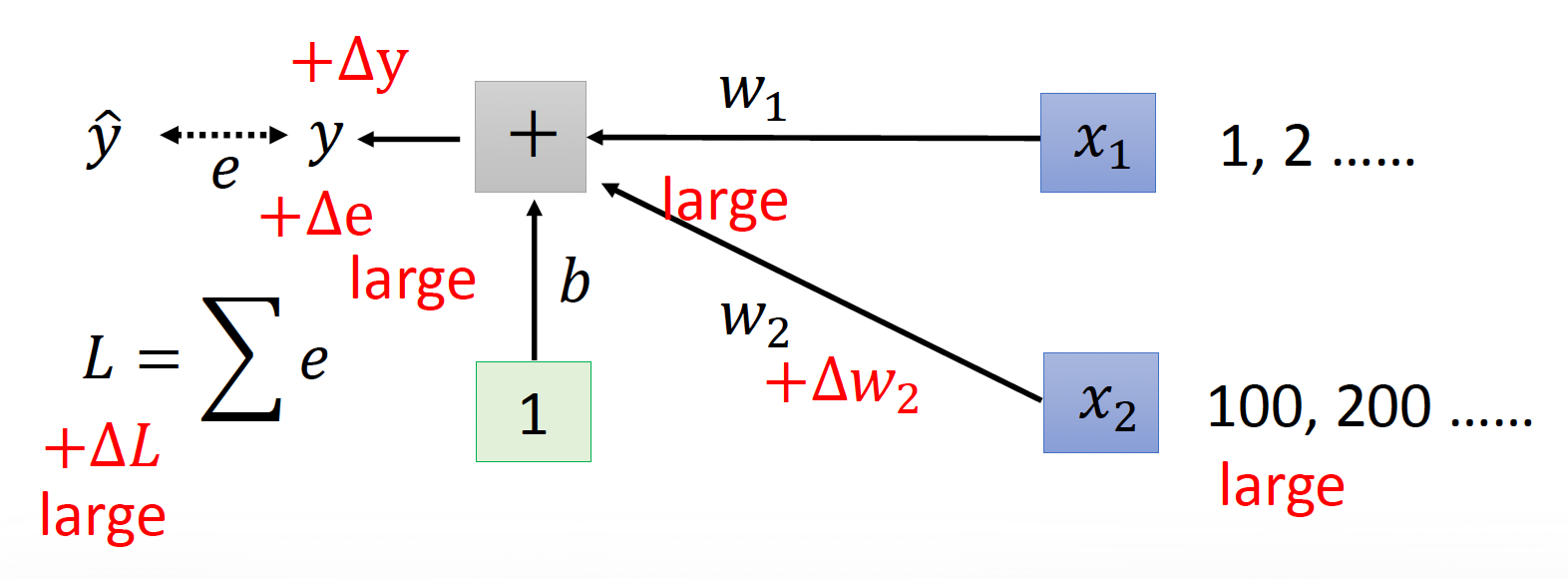
可以看到，沿着参数 \(w_1\) 变化的误差曲面较为平缓，而沿着参数 \(w_2\) 变化的误差曲面就比较陡峭。

一种可能的解释是：

• 假如对 \(w_1\) 做一个微小扰动 \(\Delta w_1\)，如果对应的输入值 \(x_1\) 很小的话，那么该扰动对误差的影响 \(\Delta L\) 也不会很大。

  

• 假如对 \(w_2\) 做一个微小扰动 \(\Delta w_2\)，如果对应的输入值 \(x_2\) 较大的话，那么该扰动对误差的影响 \(\Delta L\) 就相对较大。

  

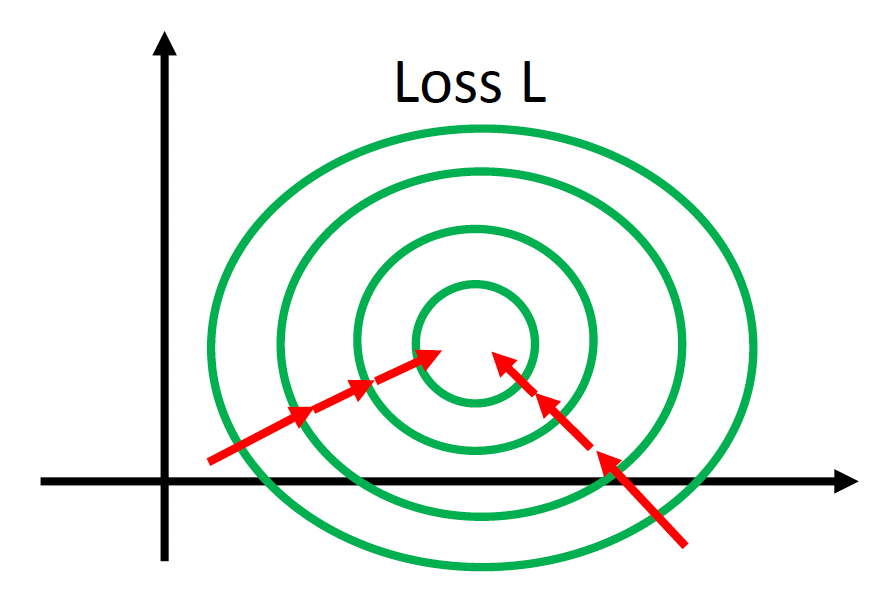
现在，我们的目标是让误差曲面无论沿 \(w_1\) 变化还是沿 \(w_2\) 变化，变化率的差别应尽可能接近，也就是让误差曲面变成这样：

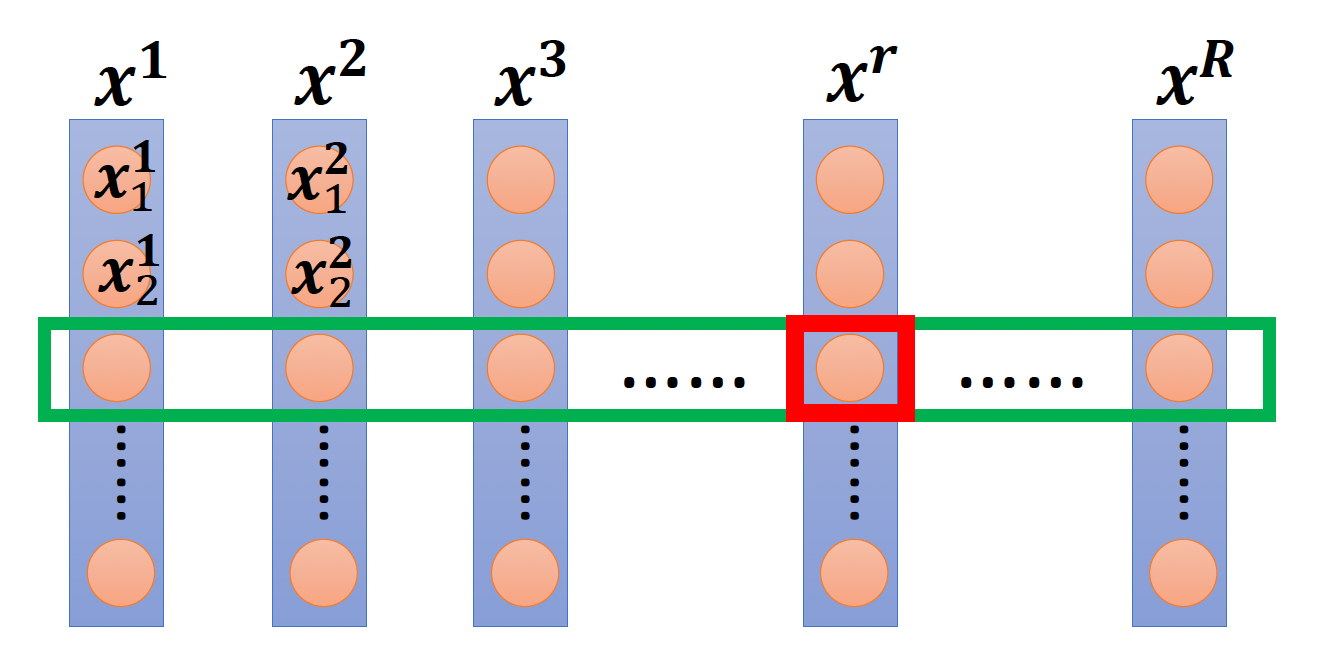
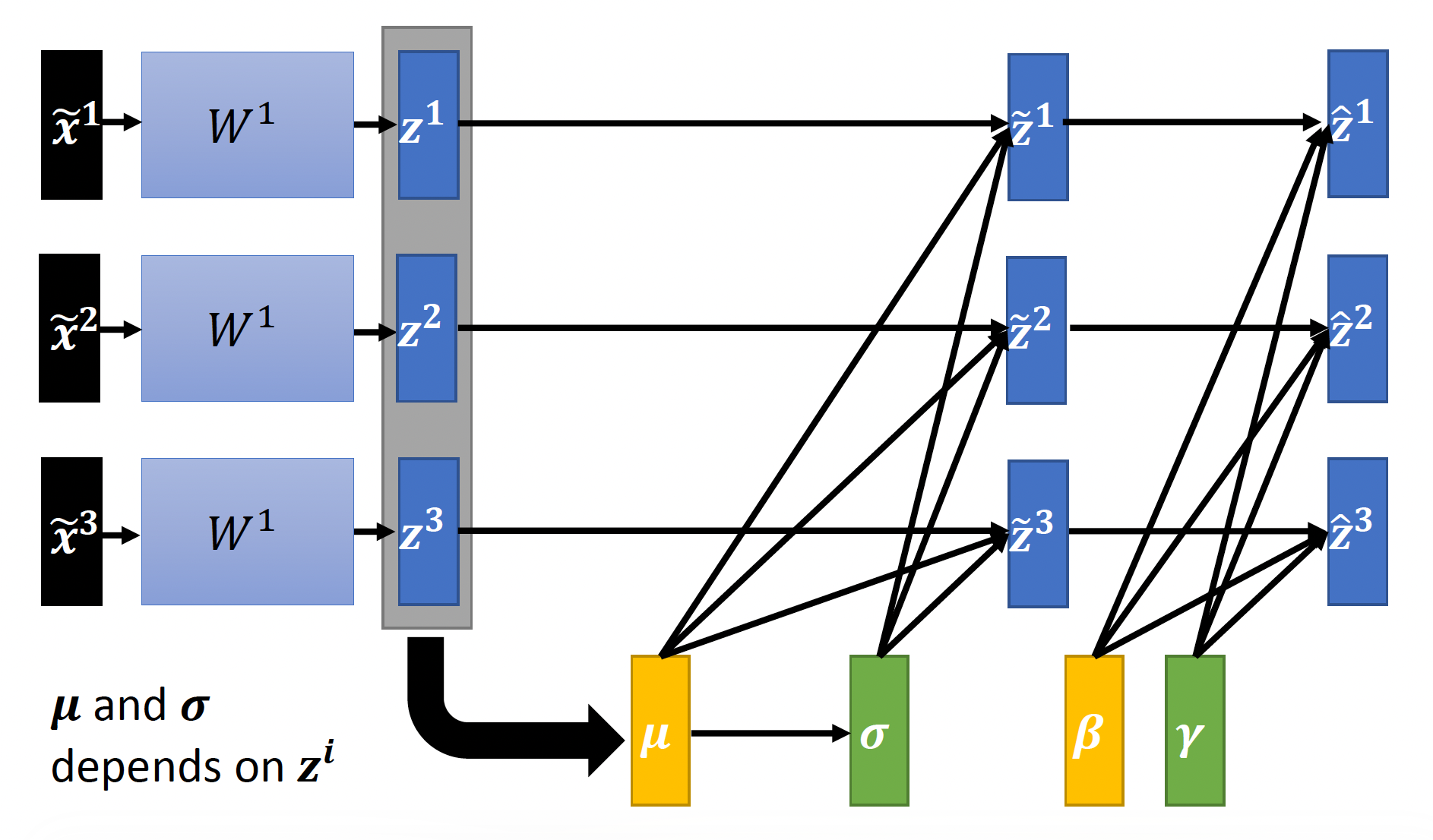
再来看特征归一化(feature normalization) 的操作。下图给出了 \(R\) 个输入向量，每个输入向量 \(x^r\) 的每个元素对应一个维度（用绿色方框框出）。对于每个维度 \(i\)，记均值为 \(m_i\)，标准差为 \(\sigma_i\)。

那么第 \(r\) 个向量在第 \(i\) 个维度上的归一化结果 \(\widetilde{\bm{x}}_i^r \leftarrow \dfrac{\bm{x}_i^r - m_i}{\sigma_i}\)。而归一化操作能确保所有维度的均值为 0，标准差为 1。

一般来说，特征归一化能让梯度下降收敛得更快。

接下来考虑特征归一化在深度学习中的应用：

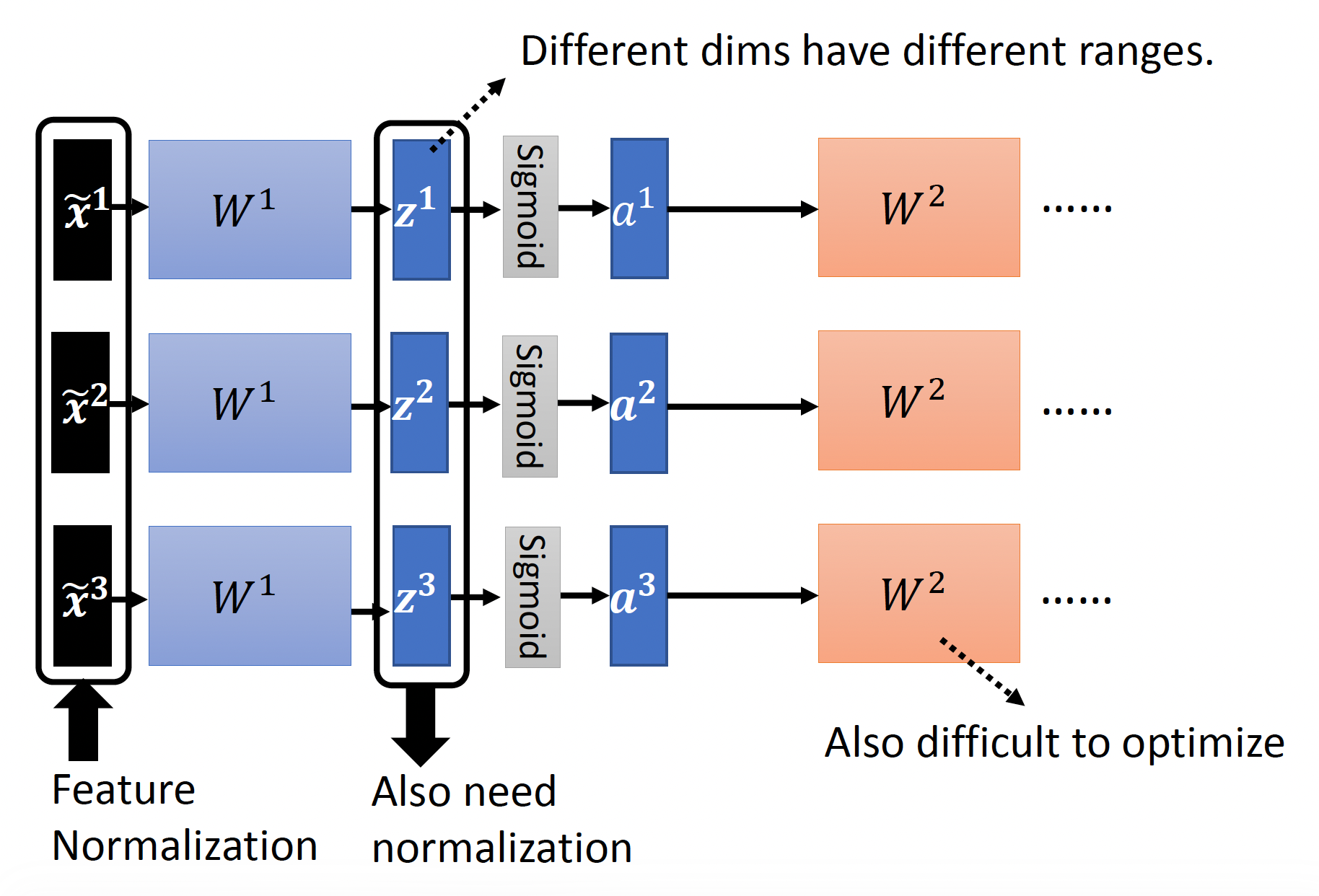
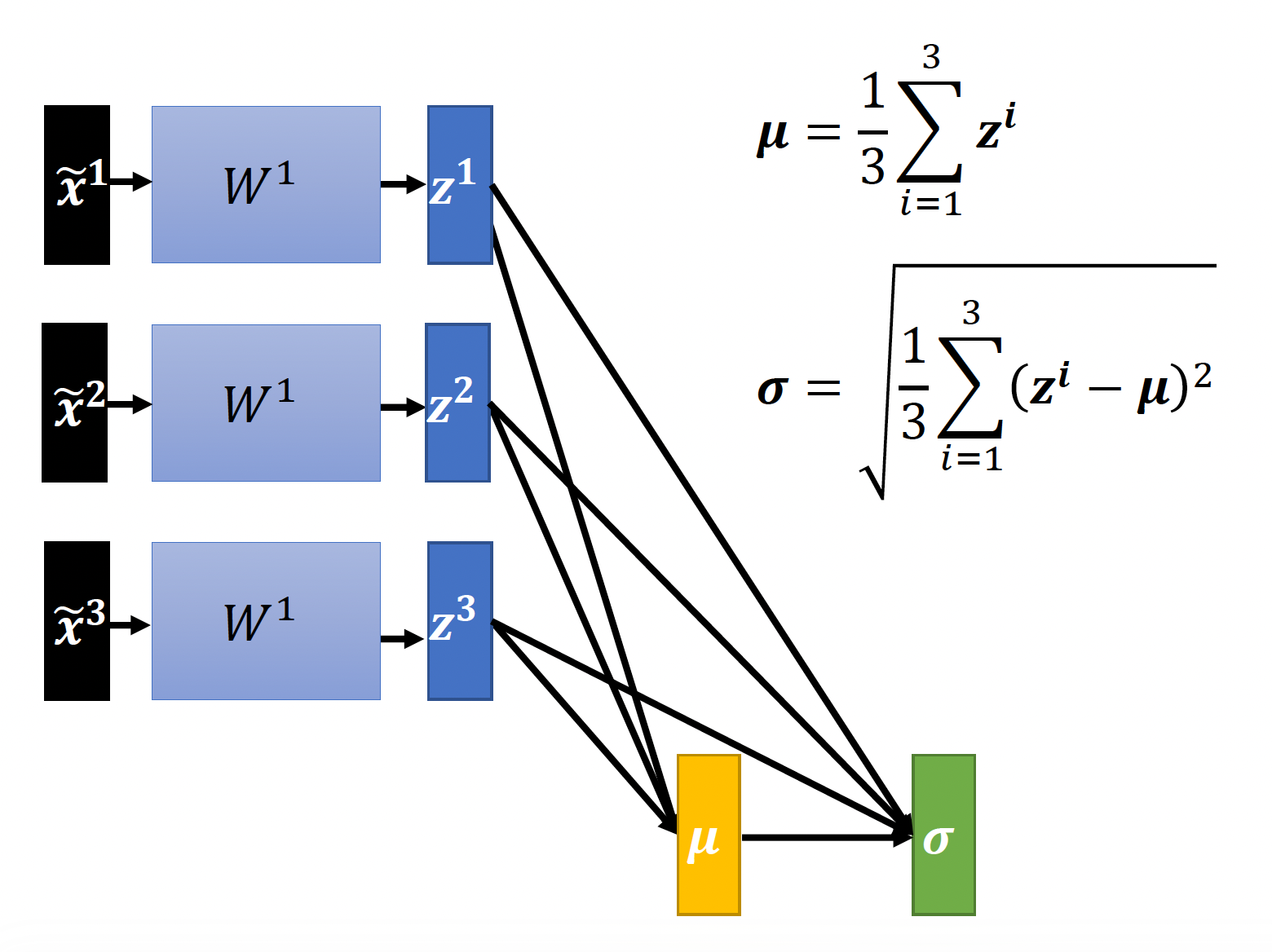
我们将特征归一化后的输入向量丢到隐藏层中继续计算，中间会得到与参数矩阵相乘后的向量 \(\bm{z}\) 和输出向量（或者是下一层的输入向量）\(\bm{a}\)。显然，在进行下一层的计算前也要进行归一化处理，那么到底是归一化 \(\bm{z}\) 还是归一化 \(\bm{a}\)。从实践上来看，两者效果差不多，而且当激活函数是 sigmoid 的时候对 \(\bm{z}\) 做归一化可能更好，所以后面我们就认准对 \(\bm{z}\) 做归一化。计算过程如下：

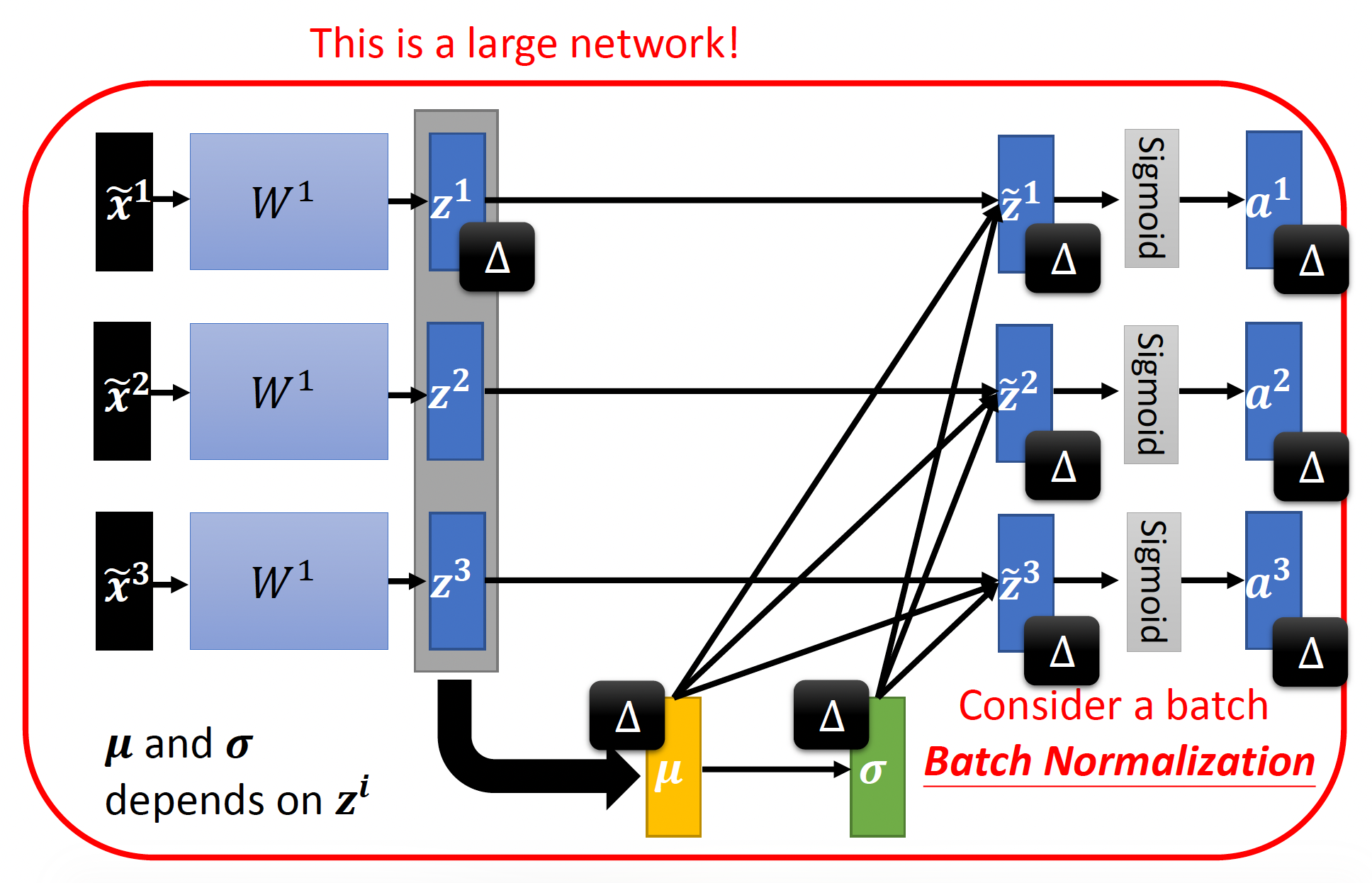
上述操作有个问题：如果这个网络接收的输入量很大很大（这里只画出了 3 个），那么 \(\mu\) 和 \(\sigma\) 的计算量也会很大。更麻烦的是，如果其中一个输入量发生了小小的改动 \(\Delta\)，那就会影响到 \(\mu, \sigma\) 的计算，从而影响到所有输入量对应的输出量的计算（“牵一发而动全身”）。

在硬件资源有限的情况下，这种计算量肯定是吃不消的。所以实际上我们不会一次性去看整个网络的输入，而是一批批地看（每批包含的输入个数不能太少，也不能太多），这种方法就是批量归一化。

前面说过，归一化能保证结果均值为 0，标准差为 1。但有时我们不太希望有这样的限制（也许这种限制会带来负面影响），所以在归一化后可通过参数 \(\beta, \gamma\) 来修正结果（这 2 个参数是通过训练得到的）。计算公式为：\(\widehat{z}^i = \gamma \odot \widetilde{z}^i + \beta\)。

然而，在测试阶段的时候，我们无法保证测试数据都是一批批过来的（总不至于要等达到一定数量后再开始计算吧）。此时我们需要改变计算的策略：

这里的 \(\overline{\mu}, \overline{\sigma}\) 是在训练过程中从每批的 \(\mu, \sigma\) 中得到的移动平均量(moving average)。以 \(\mu\) 为例，假如我们得到了每批对应的 \(\mu\) 为 \(\mu^1, \mu^2, \dots, \mu^t\)，那么 \(\overline{\mu} \leftarrow p \overline{\mu} + (1 - p) \mu^t\)。

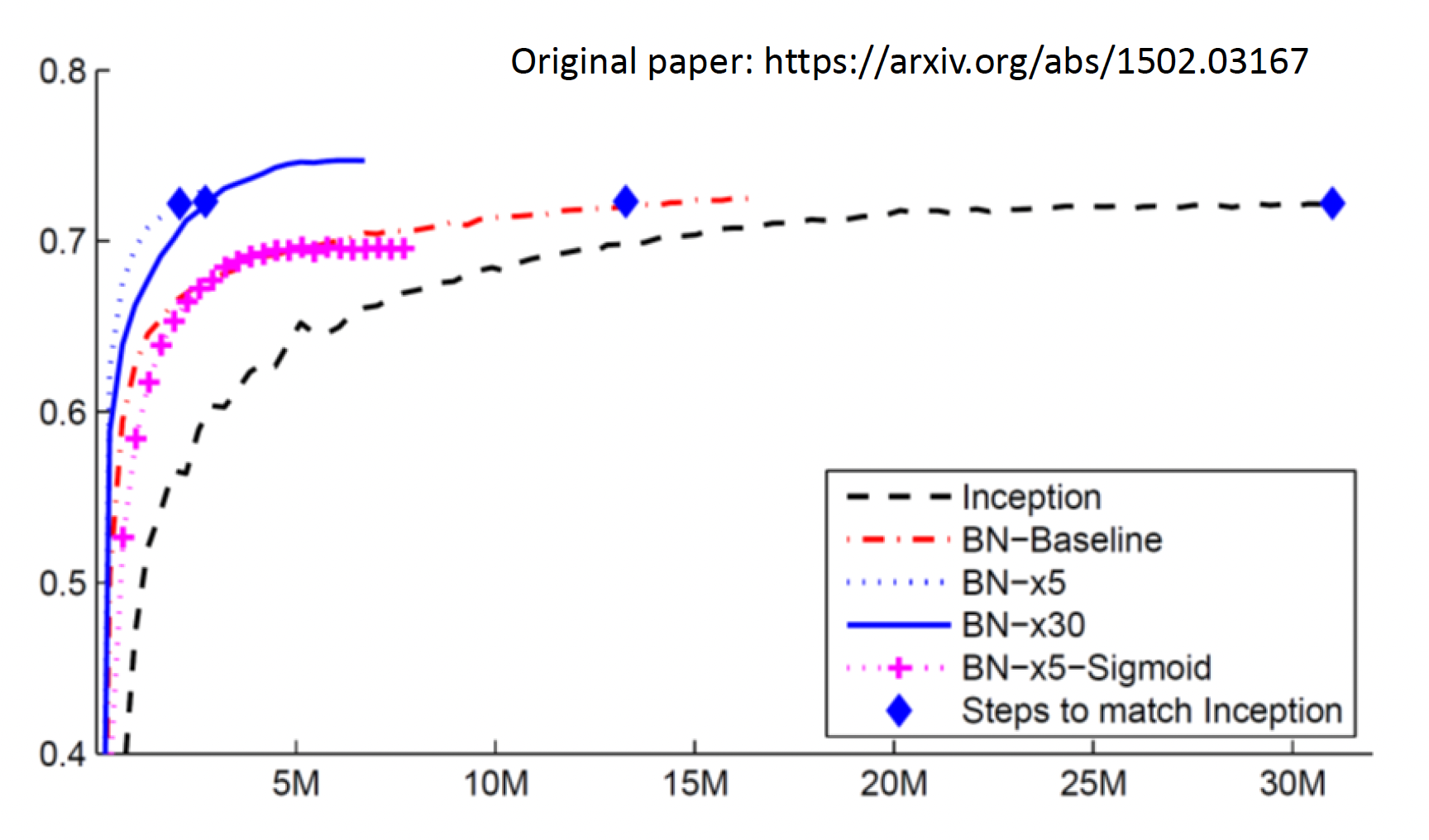
下图展现了各种方法在不同数据量的训练效果（纵轴表示准确率）

其中黑色曲线表示的是一般方法，红色曲线标识最基本的批量归一化。不难发现批量归一化相比一般方法能以更少数据达到相同的准确率，即收敛速度更快。而且如果学习速率更快的话，收敛得还要快。但并不是学习速率越大越好（可以看到 BN-x30 不如 BN-x5）。

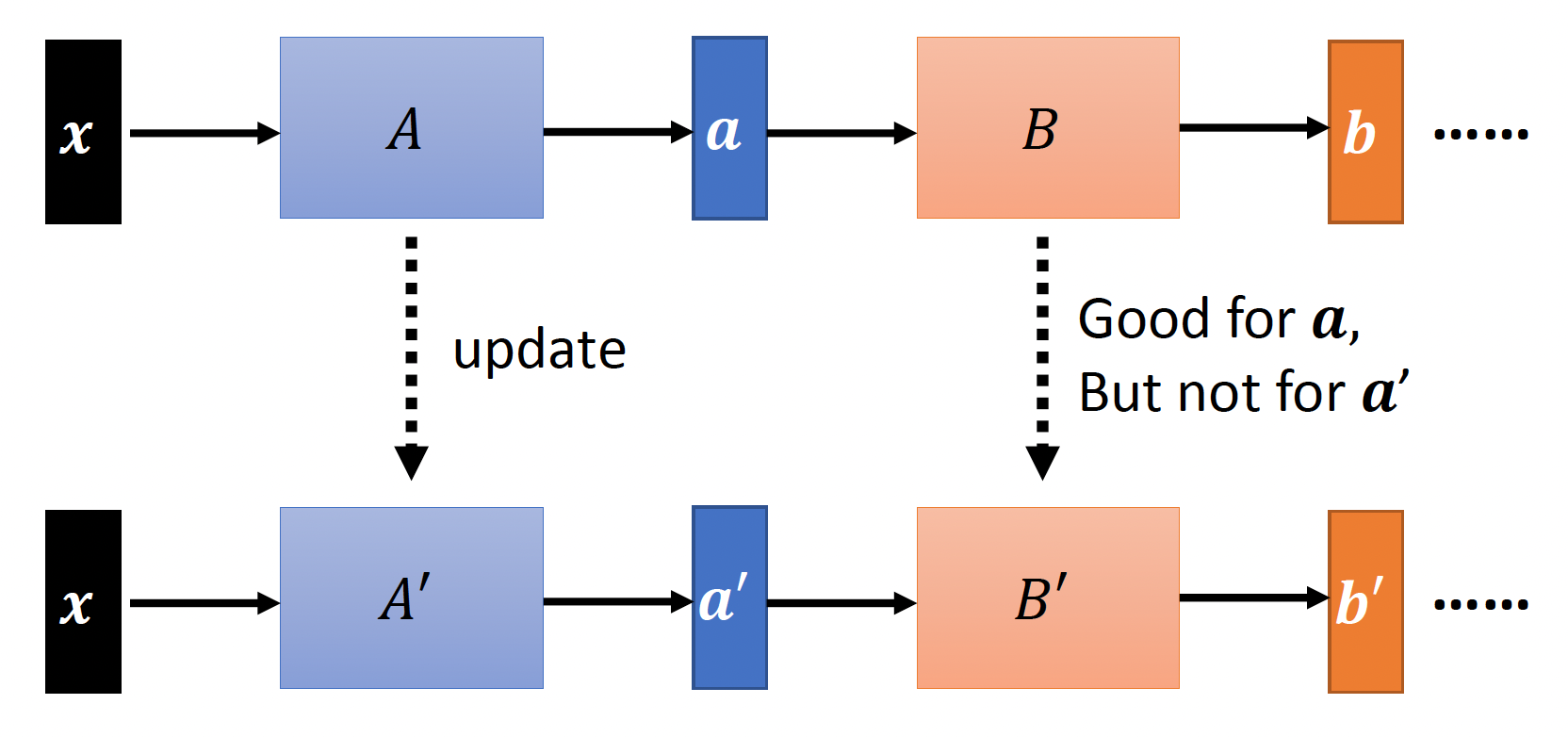
那么为什么批量归一化能够取得这样好的效果呢？有人提出了一种称为内部协变量偏移(internal covariate shift) 的观点。来看这张图：

假如某一层的参数矩阵从 \(A\) 变成了 \(A'\)，这样我们得到了更好的输出 \(a'\)，但是这种改变会影响到后面隐藏层的计算——原来下一层的参数矩阵 \(B\) 更适合算 \(a\) 而不是 \(a'\)，所以问题变得更复杂了。而批量归一化能够保证 \(a\) 和 \(a'\) 有着相似的统计学信息，因此能尽量减小上述问题的影响。

然而，一篇名为 How Does Batch Normalization Help Optimization? 的 paper 通过实验反驳上述观点。它说明了内部协变量偏移不一定是训练时的问题（就算 \(a, a'\) 相差很大也不会对训练效果有太大影响），而且批量归一化不一定能够解决这个问题。此外，这篇 paper 还从实验和理论上都说明了批量归一化能够改变误差曲面的样貌。另外这篇 paper 认为批量归一化的积极影响是一种“偶然的发现”(serendipitous)。

更多的归一化方法

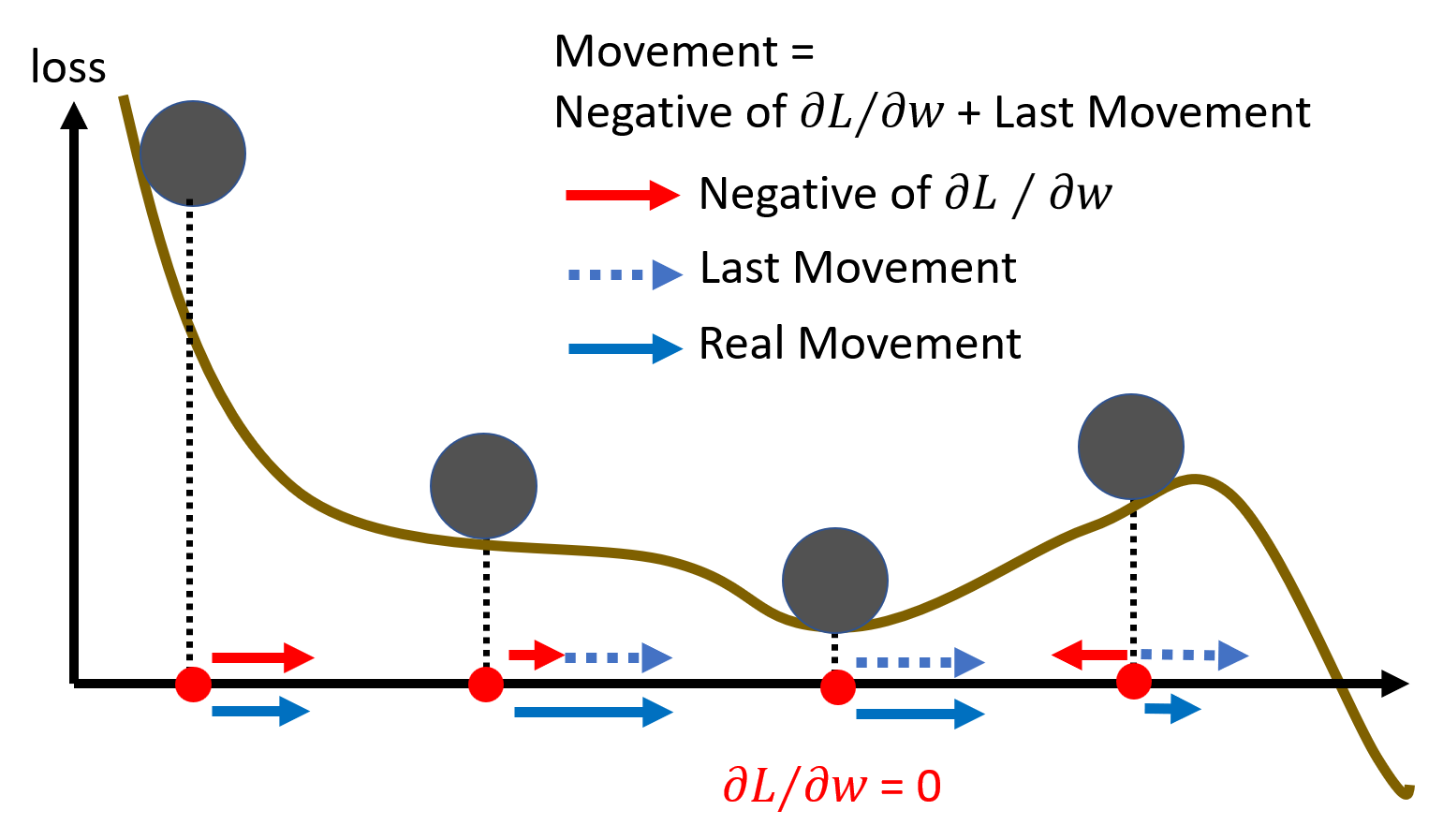
Momentum⚓︎

在梯度下降法中，当梯度接近于 0 的时候，就会停在这些点上了。但是在物理世界中，即使某段路相当平坦（鞍点），甚至是一个小坑（局部最小点），由于物体具有惯性，因此还会继续移动，不会马上停下来。这给我们改进梯度下降法提供了一个不错的想法——引入动量(momentum) 的概念，让之前的移动过程影响当下的移动过程，有助于摆脱局部最小的困境。

对比

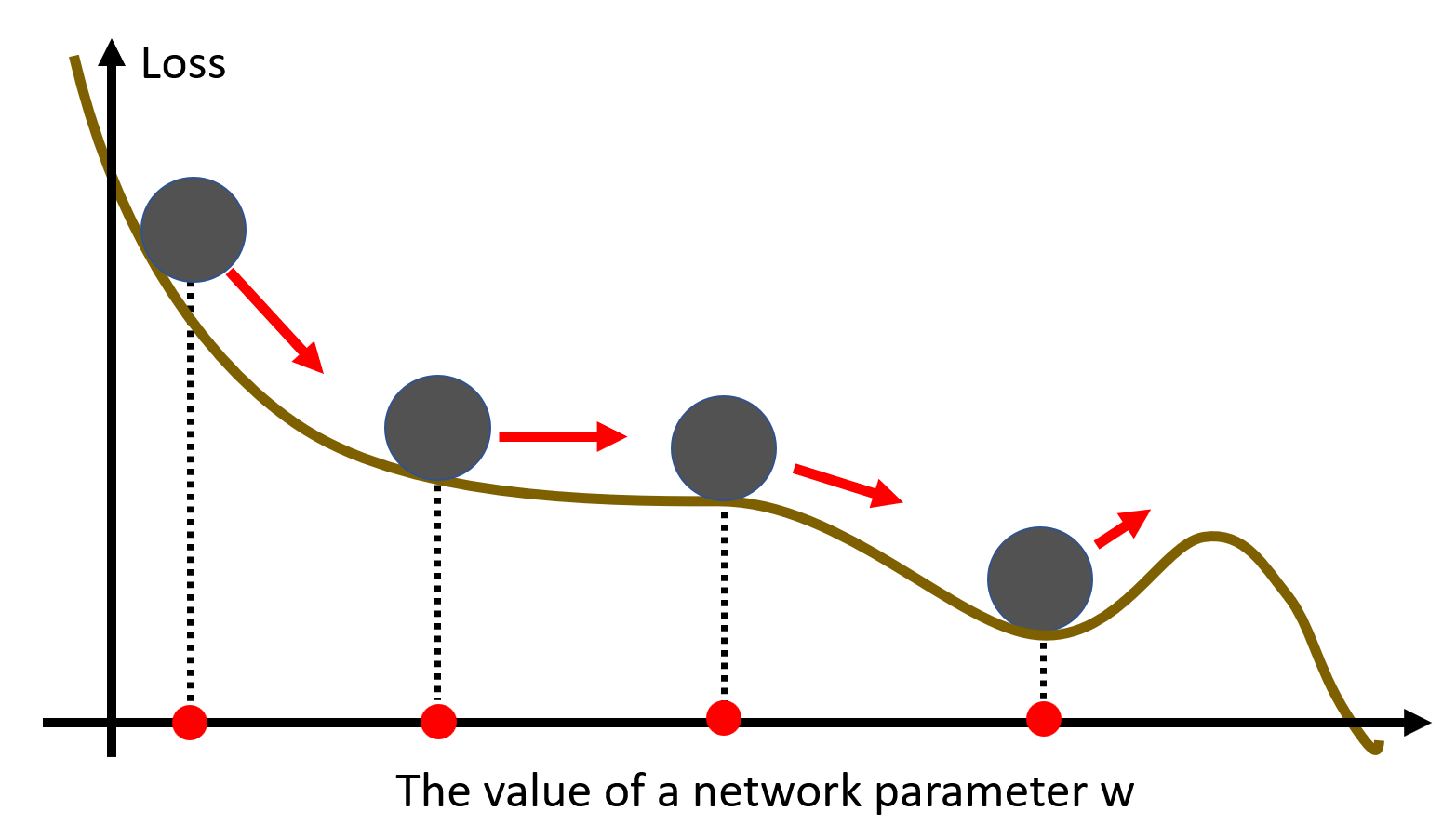
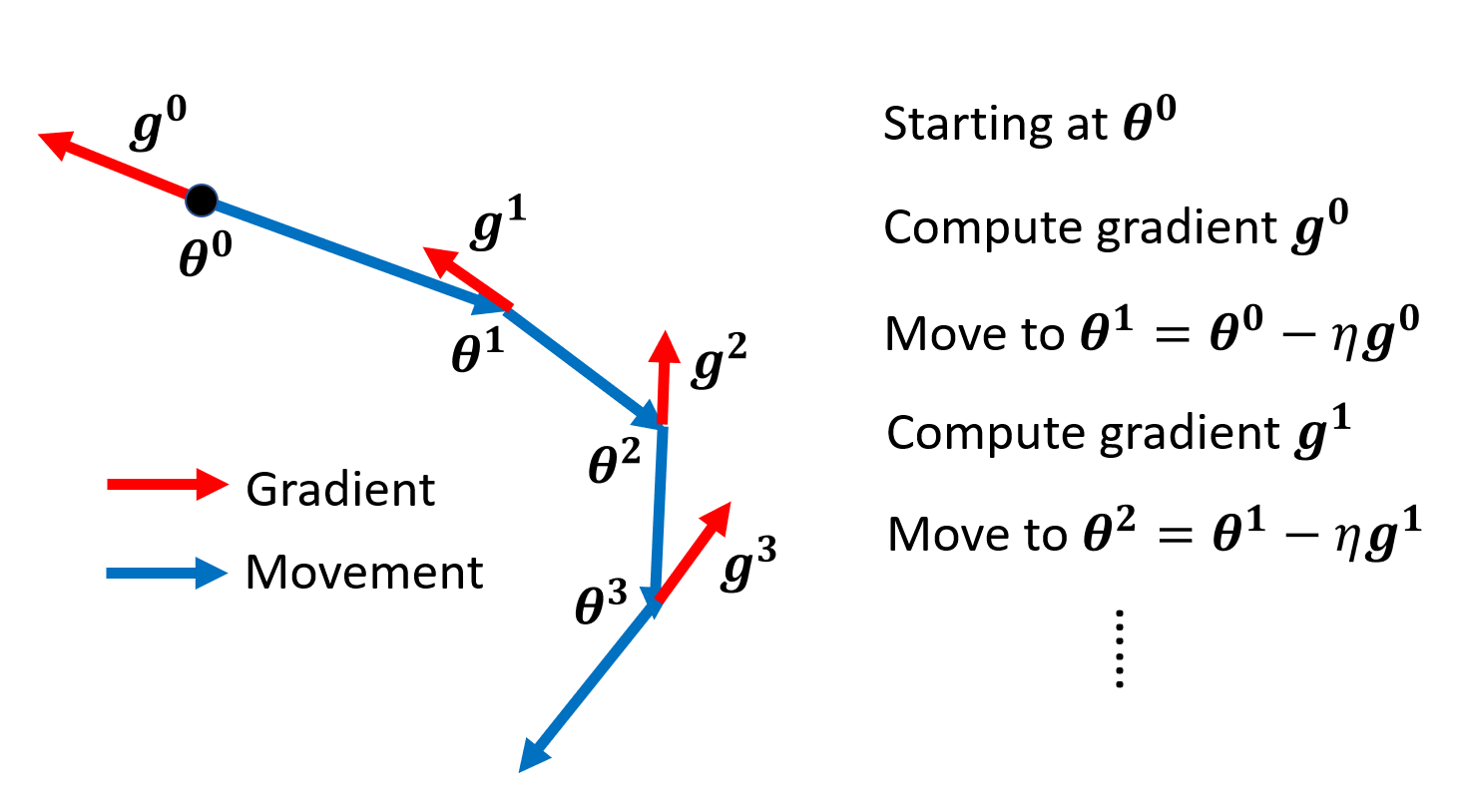
在正式介绍该方法前，先来总结一下一般的梯度下降法，如下图所示。由于比较直观，这里就不再赘述了。

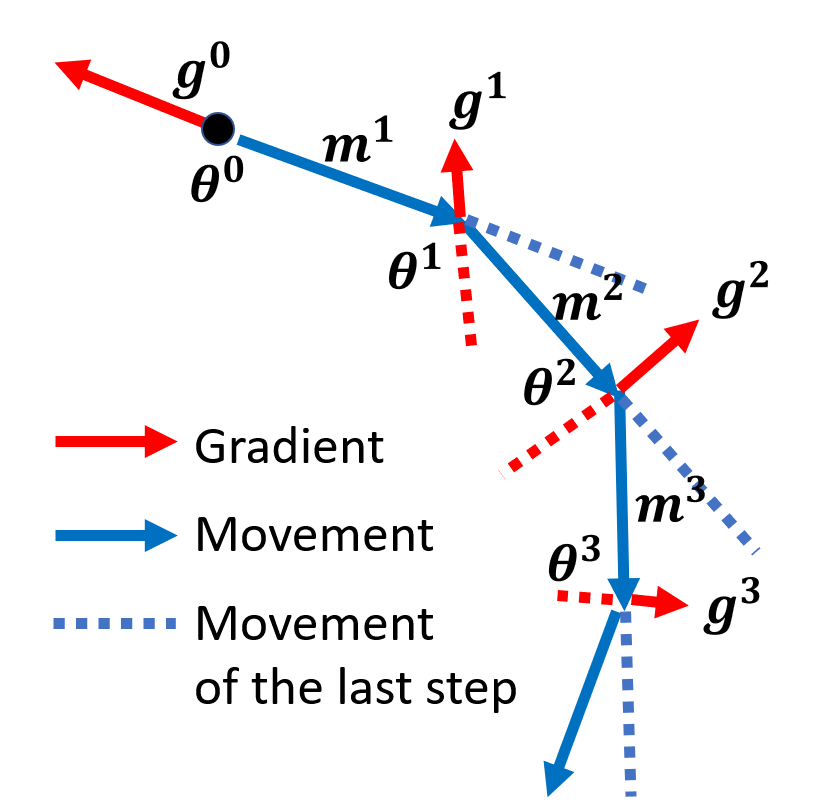
现在引入动量，那么每步的移动就是上一步的移动与当前梯度的差，具体来说：

• 令初始点为 \(\bm{\theta}^0\)，移动量 \(\bm{m}^0 = 0\)，梯度 \(\bm{g}^0\)
• 第一步移动 \(\bm{m}^1 = \lambda \bm{m}^0 - \eta \bm{g}^0\)，下一个目标点 \(\bm{\theta}^1 = \bm{\theta}^0 + \bm{m}^1\)，然后计算梯度 \(\bm{g}^1\)
• 第二步移动 \(\bm{m}^2 = \lambda \bm{m}^1 - \eta \bm{g}^1\)，下一个目标点 \(\bm{\theta}^2 = \bm{\theta}^1 + \bm{m}^2\)，然后计算梯度 \(\bm{g}^2\)
• 以此类推 ...

上述过程如下所示：

观察发现，第 \(i\) 次移动量为前几次梯度 \(\bm{g}^0, \bm{g}^1, \dots, \bm{g}^{i-1}\) 的加权和，比如：

有了动量后，对于本节最开始提到的例子，现在的优化过程就可能像下图一样，不会被某些关键点给困住。

Adaptive Learning Rate⚓︎

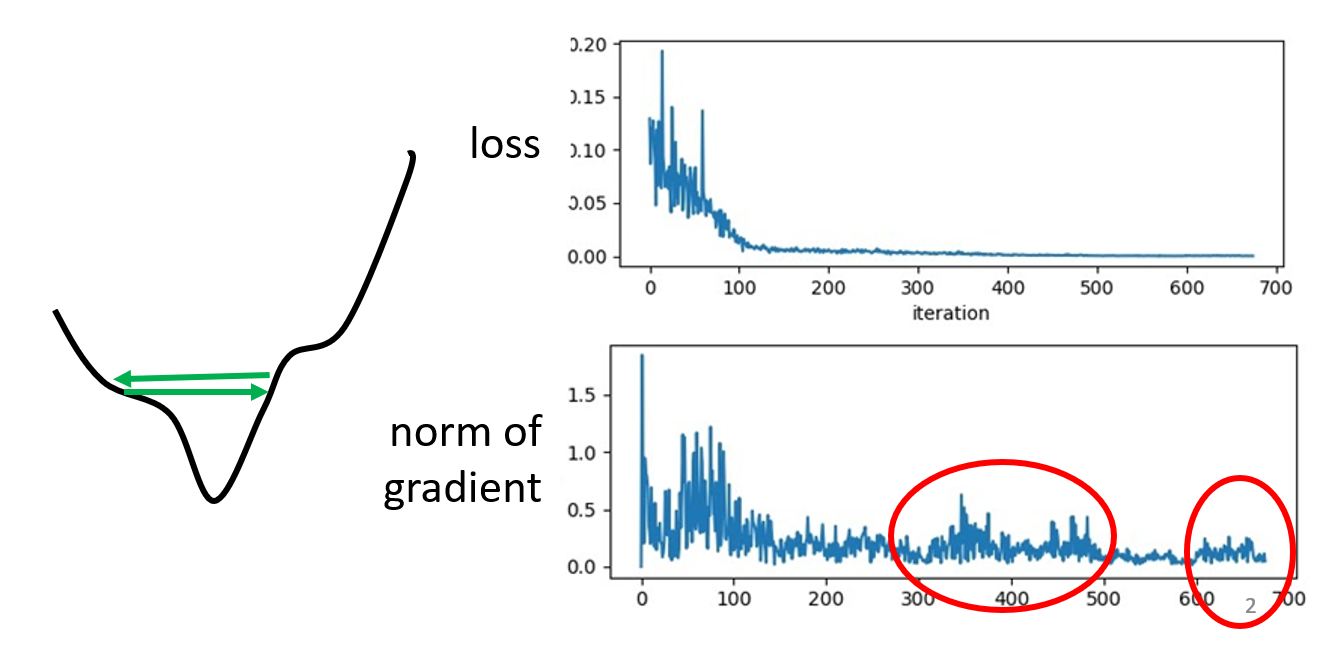
不少人会认为在训练过程中，如果模型无法得到进一步的优化（假定使用梯度下降法优化），那么应该是参数到达关键点附近的位置。然而，实际上并不一定是这种情况 ...

如上图所示，虽然损失值随着迭代次数的增加而逐渐减小，最终趋于稳定，但是梯度的模值仍然不断跳动，这就说明参数并不一定抵达关键点，而有可能出现了像左图所示的情况：由于每次迭代更新的步幅（学习速率）过大，导致参数点在“山坡”之间来回跳动，但此时的梯度值并不接近于 0。接下来再看一个例子：

例子

假如有一张凸 (convex) 的误差曲面，如下所示：

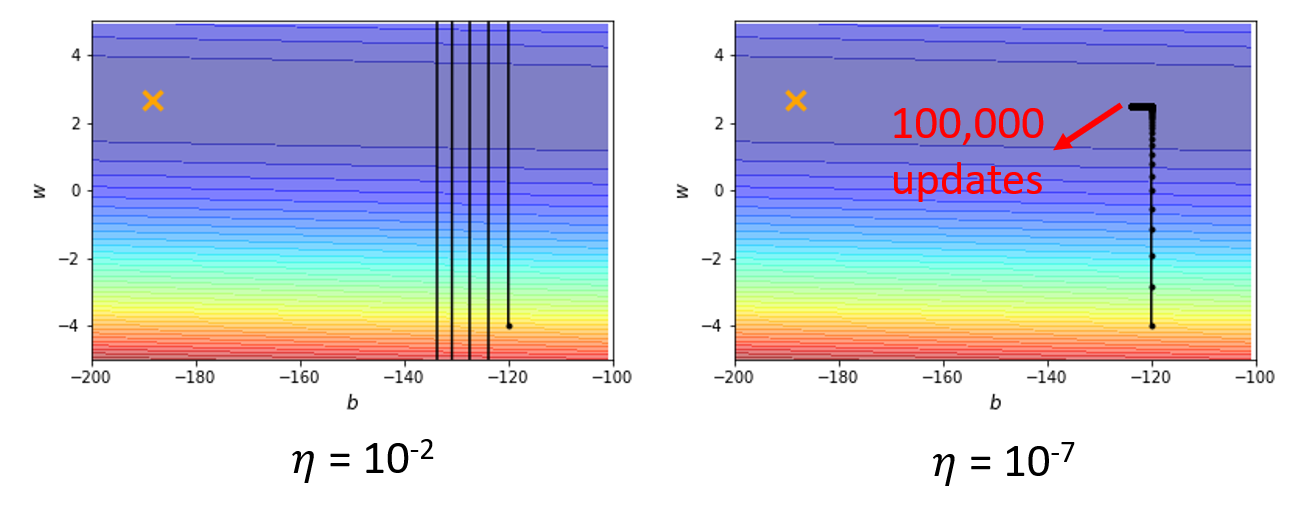
下面是不同学习速率下模型的优化过程：

• 如果学习速率过大，每次迭代更新的步幅就会很大，有些“刹不住车”，难以减小损失
• 如果学习速率过小，每次迭代更新的步幅就会很小，因此当参数点到达了平缓的（梯度较小）区域时，更新速度就会变得很慢很慢，效率就太低了

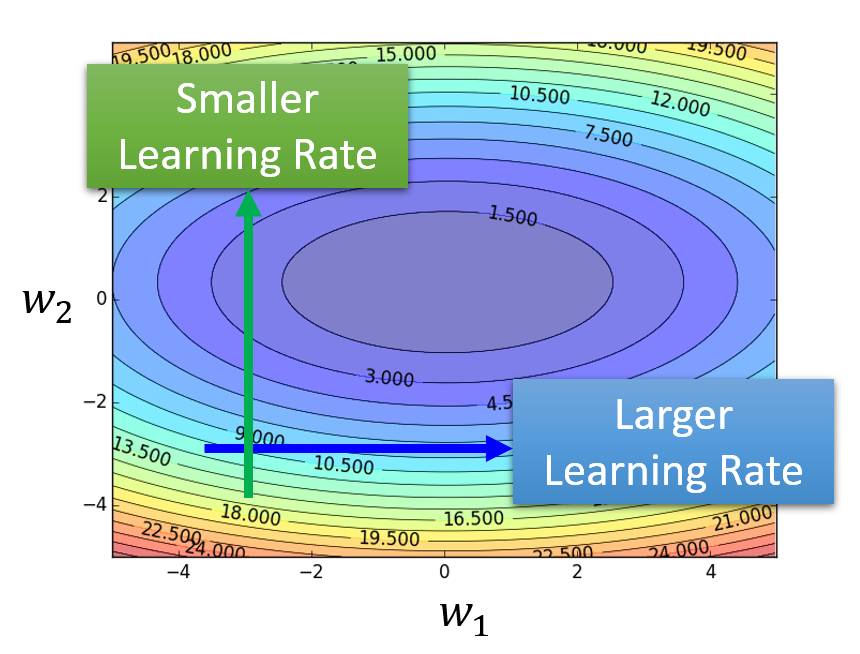
综上，如果学习速率保持不变，就很难达到理想的优化效果。因此，不同的参数应当有不同的学习速率，以适应具体情况：

• 当参数在陡峭的误差曲面上的时候，学习速率应该变得更小
• 当参数在平坦的误差曲面上的时候，学习速率应该变得更大

Adagrad⚓︎

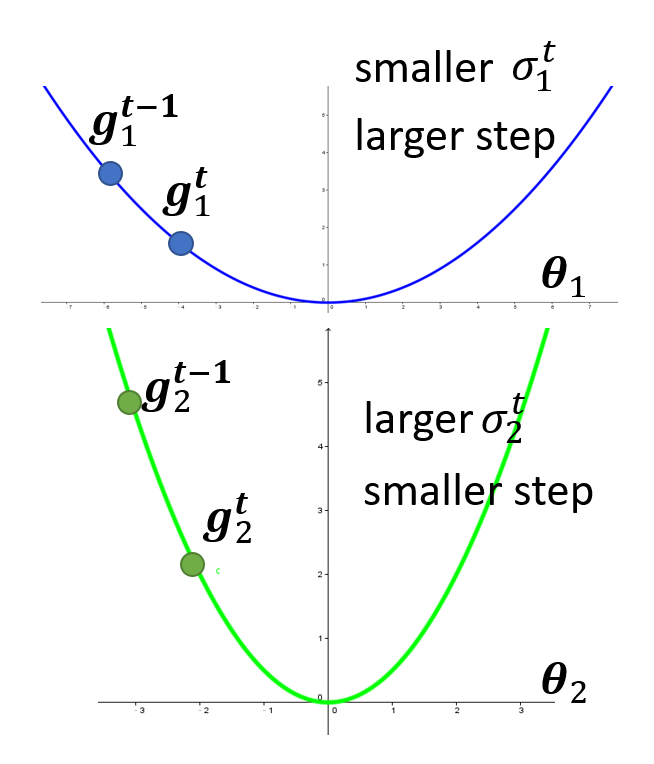
在原来的第 \(t\) 次迭代优化中，参数更新的式子为：\(\theta_i^{t+1} = \theta_i^t - \eta \bm{g}_i^t\)，其中 \(\bm{g}_i^t = \dfrac{\partial L}{\partial \bm{\theta}_i} \Big|_{\bm{\theta} = \bm{\theta}^t}\)，此时的学习速率是固定的 \(\eta\)。为了让学习速率与参数有关，我们将迭代更新的式子转化为：

其中 \(\sigma_i^t\) 的值为前 \(t\) 次（\(0 \sim t - 1\)）迭代的梯度的均方根(root mean square)，即：

实际上，这种优化方法称为 Adagrad。这样，对于不同的参数，便可以做到在梯度小的地方，迈的步子更大；在梯度大的地方，迈的步子更小。

RMSProp⚓︎

Adagrad 的问题

问题 1 问题 2

然而，上述方法仍然有缺陷。对于更为复杂的误差曲面，即使是同一个参数，沿同一个方向（梯度）变化时，所经过的误差曲面有平坦的，也有陡峭的。上述方法在这种情况下仍然保持相同的学习速率，而这是不符合我们预期的。

不难发现，Adagrad 在更新参数的时候会不断累积之前的梯度，那么如果在训练开始的时候，梯度就非常大的话，那么 \(\sigma\) 也变得非常大，所以没走几步就走不下去了，影响到训练的效果了。

所以，接下来引入一种更好的优化方法，称为 RMSProp。它的迭代更新公式与 Adagrad 类似，区别在于 \(\sigma_i^t\) 的公式发生了变化：

此时 \(\sigma_i^t\) 的值不仅和当前的梯度有关，还受之前迭代的梯度的影响（可通过展开 \(\sigma_i^t\) 发现）。此外，我们可以通过超参数 \(\alpha \in (0, 1)\) 来调整 \(\sigma_i^t\) 中 \(\bm{g}_i^t\) 以及 \(\sigma_i^{t-1}\) 的比例。如果 \(\alpha\) 较小，那么当前梯度对 \(\sigma_i^t\) 的影响更大，而之前的梯度影响更小。下图展现了使用 RMSProp 优化的大致效果：

Adam⚓︎

将前面介绍过的动量方法与 RMSProp 结合起来，我们便可以得到一种很常用的优化方法，称为 Adam，其算法实现如下所示：

更新公式为：\(\theta_i = \theta_{i-1} - \dfrac{\eta}{\sqrt{\hat{v_t}} + \varepsilon} \hat{m_t}\)，其中：

• \(\hat{m_t} = \dfrac{m_t}{1 - \beta_1^t} = \dfrac{\beta_1 m_{t-1} - (1 - \beta_1)g_{t-1}}{1 - \beta_1^t}\)
  • 当 \(t\)（迭代次数）比较小的时候，\(\hat{m_t}\) 会比较大，因为初始情况下不会有多少动量，所以需要适当增大，以避免在一开始就陷入关键点的情况出现；随着迭代次数的增加，\(\hat{m_t}\) 会越来越小，趋于稳定
• \(\hat{v_t} = \dfrac{v_t}{1 - \beta_2^t} = \dfrac{\beta_2 v_{t-1} + (1 - \beta_2)(g_{t-1})^2}{1 - \beta_2^t}\)
  • 其设置也和 \(\hat{m_t}\) 同理
• \(\beta_1 = 0.9\)
• \(\beta_2 = 0.999\)
• \(\varepsilon = 10^{-8}\)
  • 这些常数值是 Adam 的作者提出来的，通常不需要我们调整（调一下往往会得到更烂的结果）

Learning Rate Scheduling⚓︎

回到前面提到过的凸误差曲面的例子，如果采用 Adagrad 方法的话，结果为：

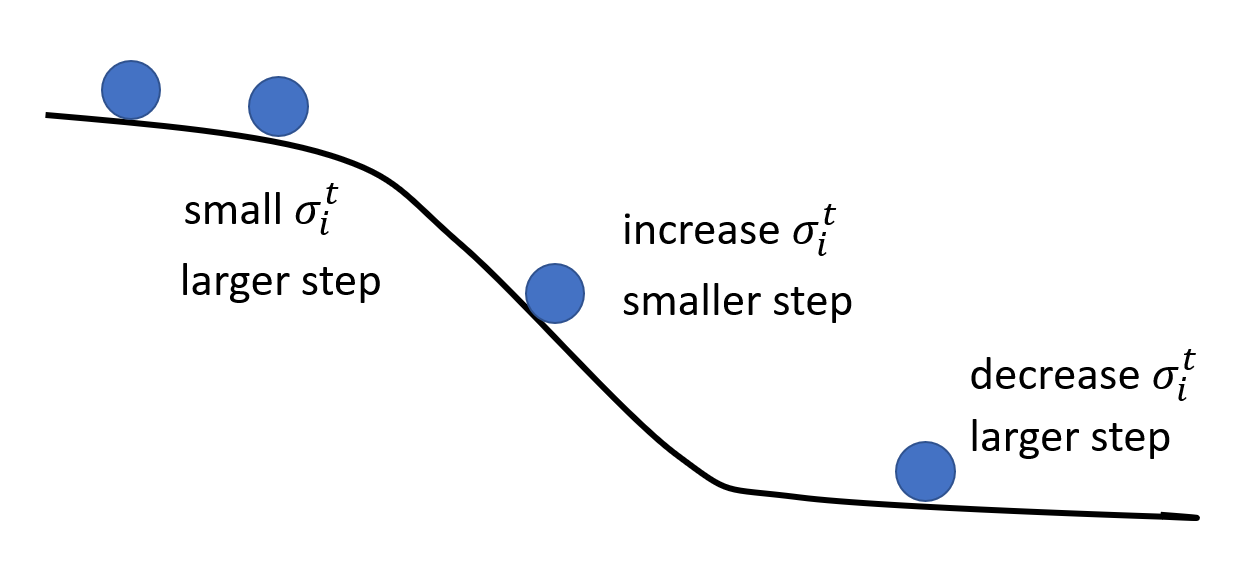
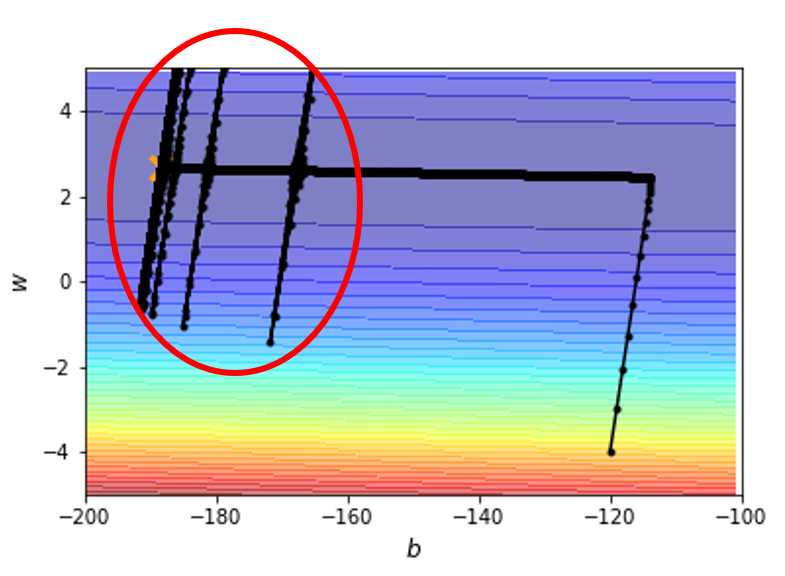
可以看到，使用这种方法可以使模型获得最优的参数，但是在优化过程中会出现红圈所示的一些“爆炸”的情况。这是因为刚开始的时候沿竖直方向的梯度很大，但后来梯度变得很小（来到了平坦的区域）；而 \(\sigma_i^t\) 会计算之前迭代过程中计算的所有梯度值，所以在平坦区域时，\(\sigma_i^t\) 会累积一些沿竖直方向很小的梯度，那么有的时候学习速率就会变得很大，因此就会一下子“飞出去”，偏离预期更新的路径。

但是该优化方法有办法修正这一偏离，因为当偏出去后，梯度就会变大，那么学习速率就会减小（好比有股“摩擦力”），于是就又慢慢回到正轨了。

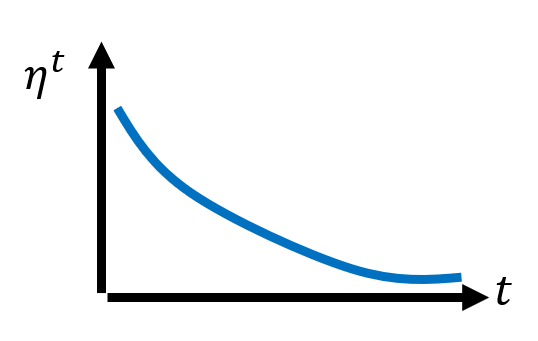
这样的优化并不完美，还有改进的空间，使其不会出现这么多的偏离现象，具体做法是使用一种叫做学习速率调度(learning rate scheduling) 的方法，让学习速率不仅随梯度（空间）变化，还随迭代次数（时间）的变化而变化（下面记第 \(t\) 次迭代的学习速率为 \(\eta^t\)）。这里介绍两种不同的方法：

• 学习速率衰减(learning rate decay)：由于随着训练的深入，模型逐渐靠近最合适的参数目标，因此学习速率会随迭代次数的增加而下降，如下图所示：

  

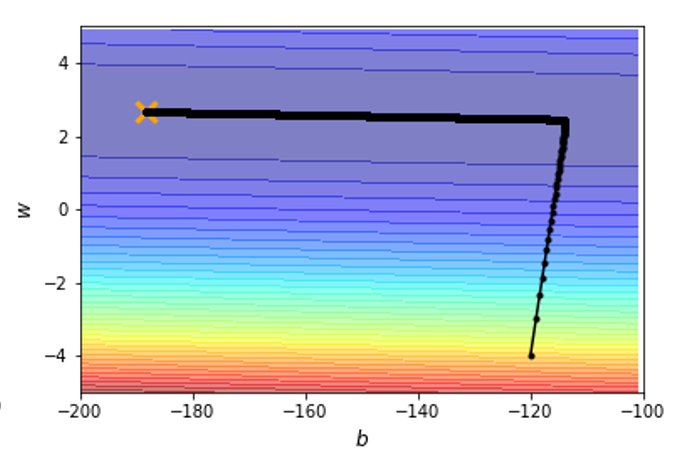
  在上面的凸误差曲面的例子中，采用该方法后的优化过程为：

  

  现在的优化过程变得非常“丝滑”了 ~

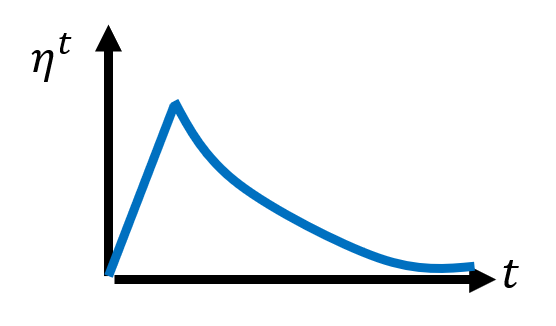
• 热身(warm up)：随着迭代次数的增加，学习速率先增后减

  

  之所以这样设定，是因为在训练刚开始的时候，还不清楚具体的误差曲面应该长什么样子，此时得到的 \(\sigma_i^t\) 就有可能偏离过大，因而需要更小的学习速率以降低影响。而随着训练的进行，会逐渐摸清楚误差曲面大致的样子，因此学习速率会逐渐上升。

  • 残差神经网络和 Transformer 都提到了这种方法
  • RAdam -> Adam + 热身

总结

结合前面提到的各种改进优化的技巧，可以得到以下式子：

\(\sigma_i^t\) 和 \(\bm{m}_i^t\) 都与前面的梯度有关，但是一个在分母，一个在分子上。然而这并不意味着两者的效果会相互抵消，因为前者是标量，只影响学习速率的大小；而后者是向量，需要考虑方向，因此两者无法完全抵消。

Other Optimizer⚓︎

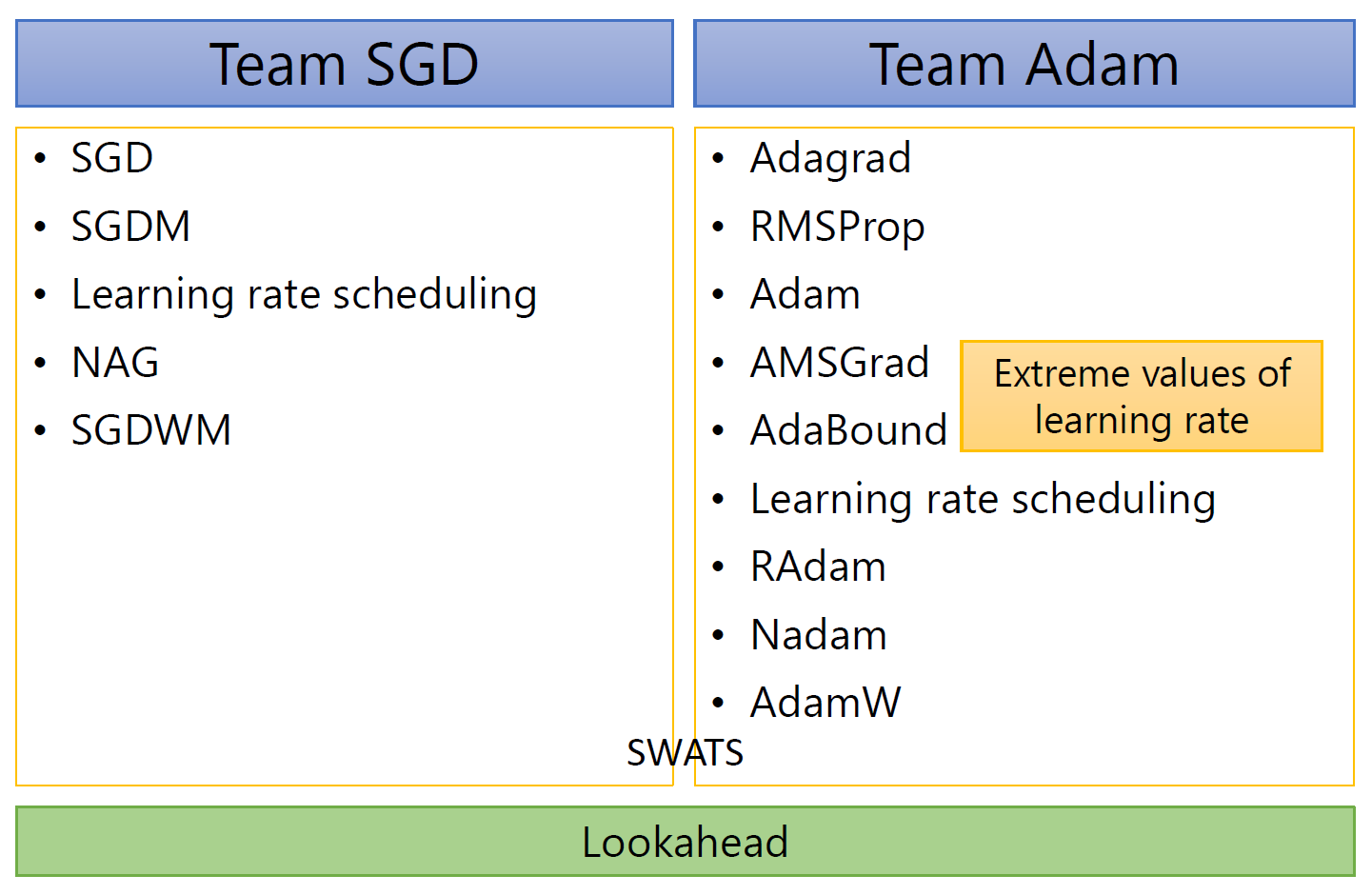
现在的优化器大多数可以分为 SGD 和 Adam 两大阵营：

• SWATS 同时利用了 SGD 和 Adam
• Lookahead 是一个对所有优化器都适用的包装器 (wrapper)，大致思路是每向前走 k 步就向后退 1 步，这样的好处是更稳定，且具备更好的泛化能力

遗憾的是，世界上没有一种通用的优化器，还需后人不断地探索出更棒的优化器！

Classfication⚓︎

前面介绍的机器学习研究的都是回归(regression) 问题，即模型根据输入数据集，输出单个标量 \(y\)，并于真实值（标签）\(\hat{y}\) 比较。现在我们来探讨分类(classification) 问题，它与回归的不同在于：模型会从多个选项（称为类别 (classes)）中挑选一个作为输出。

那我们是否可以将分类问题转化为回归问题呢？因为输出的都是单个量，那么也许可以尝试用单个标量表示挑选出来的类别；并且规定每个选项都用一个数值表示，便于将输出 \(y\) 与标签 \(\hat{y}\) 比较。然而，这样会带来一个明显的问题：类别之间的关系可不像数值之间的大小这么直接，也许类别之间的关系很复杂，也许压根没有关系，那么 \(\hat{y} - y\) 也就无法准确表示输出类别与真实类别之间的关系，所以这不是一个好方法。

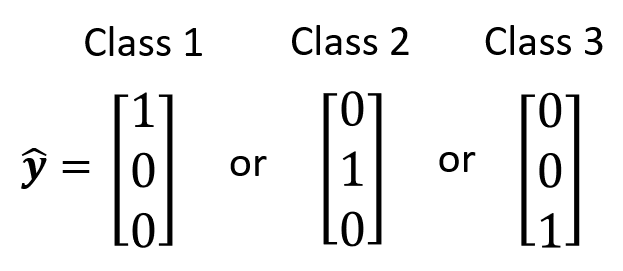
实际上，我们采用独热向量(one-hot vector) 来表示每个类别。独热向量的特点是：向量里面的元素只有 0 和 1，而且只有其中一位是 1，其余位均为 0。对于任意两个不同类别的独热向量，它们值为 1 的元素是不同的。这种方法的好处在于：任意不同两个类别之间的区别是一致的，因为它们对应的独热向量之间的距离是一样的，这样便于输出类别与真实类别的比较。

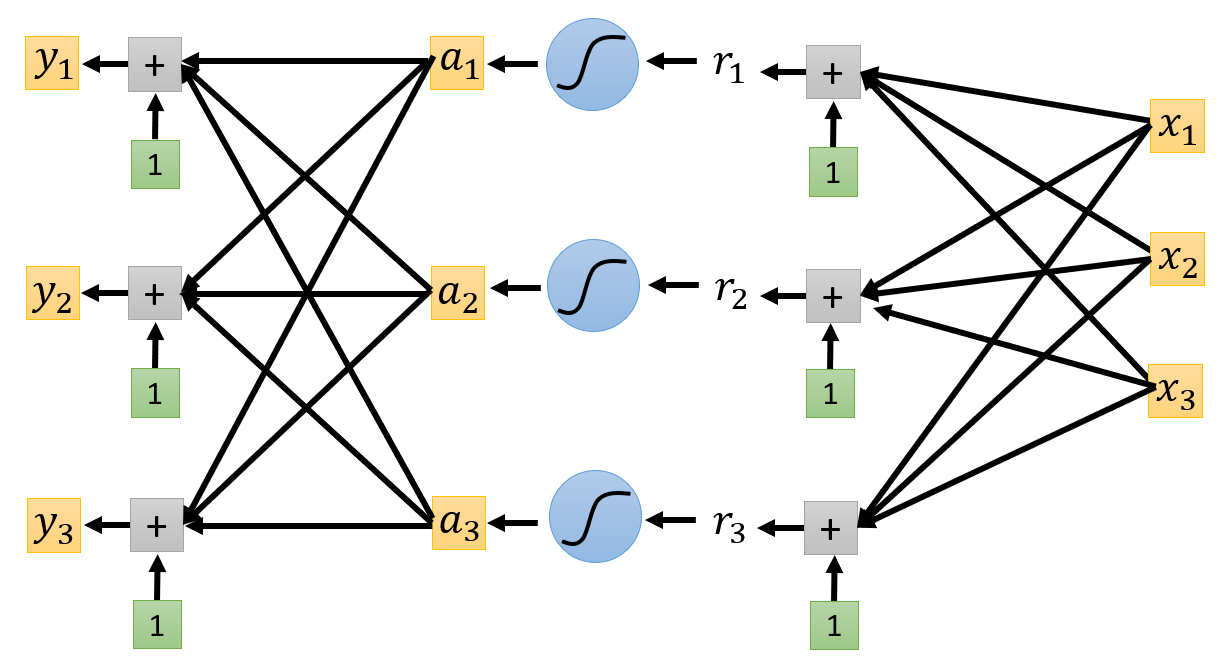
因为向量里面包含多个标量，那么模型就要从输出单个值转变为输出多个值，因此需要稍微改变一下模型的样子，如下所示：

重点关注输出部分的改变。以上图为例，现在的输出由 \(y_1, y_2, y_3\) 三部分构成，每个输出都有各自不同的权重和偏移，但接收的都是来自激活函数的输出。

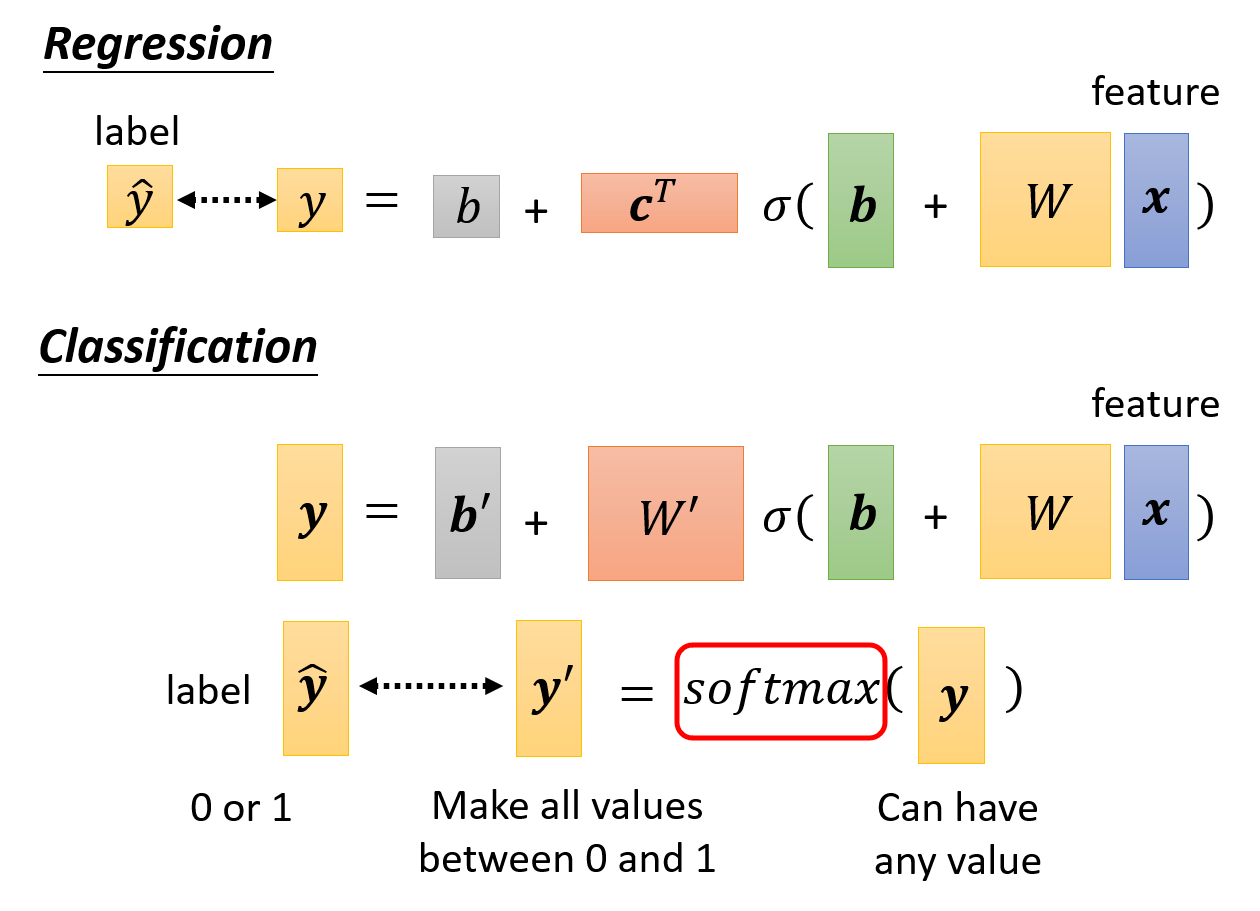
现在来比对一下回归和分类两类问题对应的模型（方程）：

相比回归模型，分类模型有一些小变化：

• 由于输出量从标量变为向量，因此对应地，权重从向量 \(\bm{c}^T\) 变为矩阵 \(W'\)，偏移从标量 \(b\) 变成向量 \(\bm{b}'\)
• 最后，还要将模型的输出值放到 softmax 函数做进一步的转化。这是因为通过模型得到的输出量可以是任意值，而我们要求的输出量中每个元素只能是 0 和 1。而 softmax 就帮我们做了这步转化，它能将任何值映射到 0 或 1 上

Softmax⚓︎

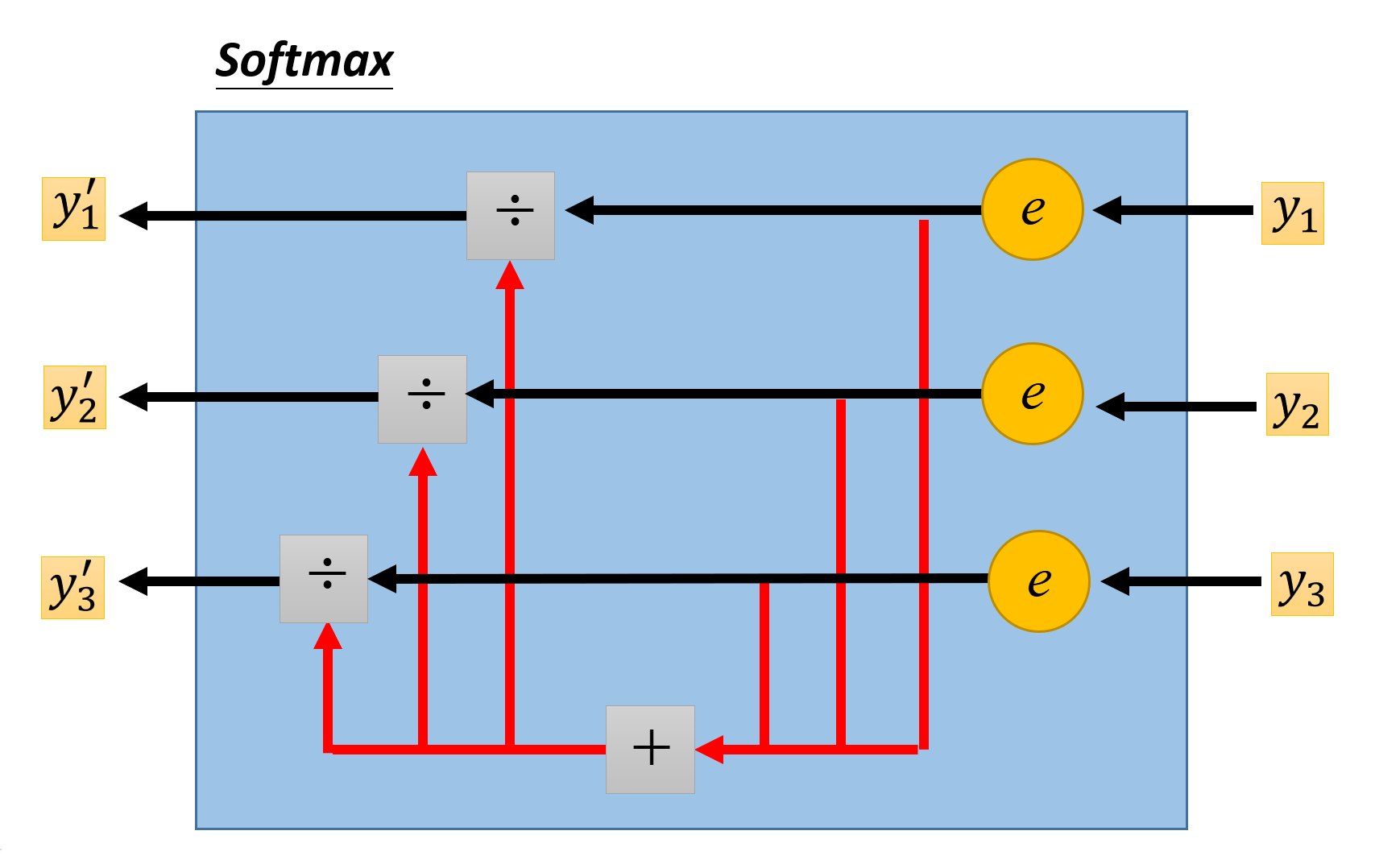
下面大致介绍一下 softmax 函数的原理。假设原始的输出向量中包含 \(y_1, y_2, y_3\) 三个元素，它们在 softmax 函数的输出分别为 \(y_1', y_2', y_3'\)，那么 softmax 的计算公式为：

下图形象展示了这一过程：

\(y_i'\) 还有以下性质：

• \(y_i' \in (0, 1)\)
• \(\sum_i y_i' = 1\)
• 对于原始输出向量中的两个元素，它们之间的差距大小也能在对应的 softmax 结果中体现出来

例子

实际上，如果只有两个类别的话，sigmoid 函数与 softmax 函数是等价的，但在这种情况下 sigmoid 函数会用的更多一些（虽然两者并没有孰优孰劣）。

Loss⚓︎

完善好我们的分类模型的输出后，现在来考虑如何计算损失。

• 损失 \(L\) 还是可以用误差的均值计算

• 误差 \(e\) 也可以继续沿用回归模型中的 MSE，即 \(e = \sum\limits_i (\hat{\bm{y}}_i - \bm{y}_i')^2\)。然而，在分类模型中，更好的误差计算方法是交叉熵(cross-entropy)，即 \(e = -\sum\limits_i \hat{\bm{y}}_i \ln \bm{y}_i'\)。虽然两者都能正确反映误差的大小，但是交叉熵更适用于分类模型的优化过程。下面通过一个例子来解释原因（严谨的数学推导过程见过去的视频）：

  例子

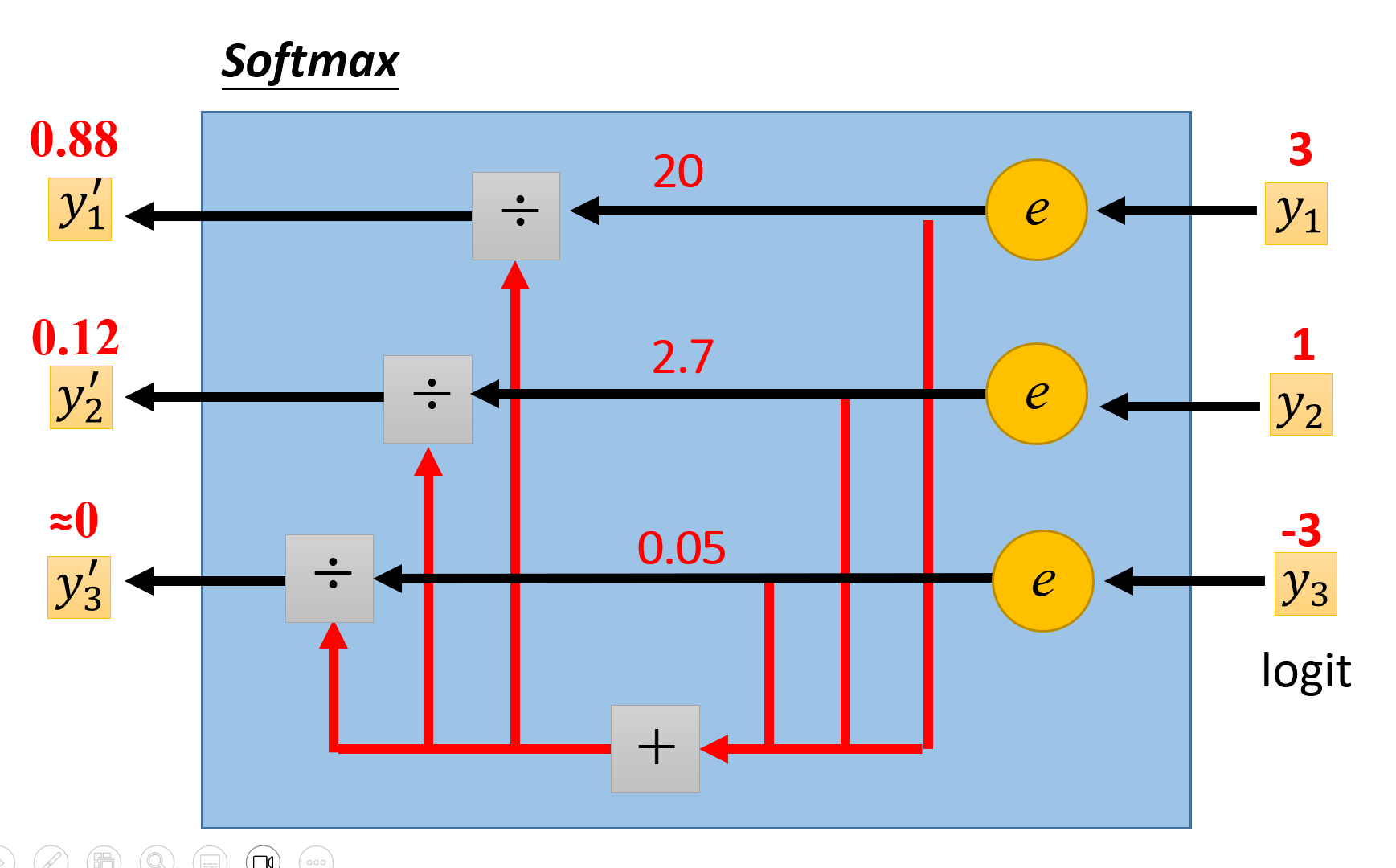
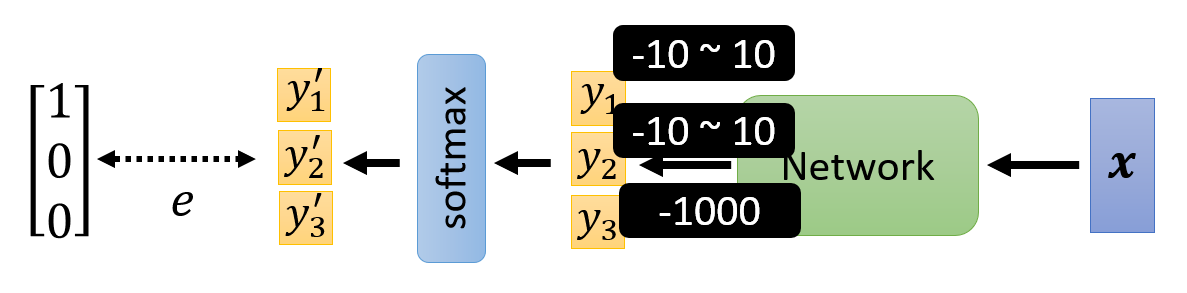
  给定以下分类模型：

  

  • 方便起见，规定输出量的范围为：\(y_1, y_2 \in [-10, 10]\)，\(y_3 = -1000\)（很小的常量，通过 softmax 后就接近于 0）
  • 标签为 \(\begin{bmatrix}1 \\ 0 \\ 0\end{bmatrix}\)

  现在来比较通过 MSE 和交叉熵得到的误差曲面：

  

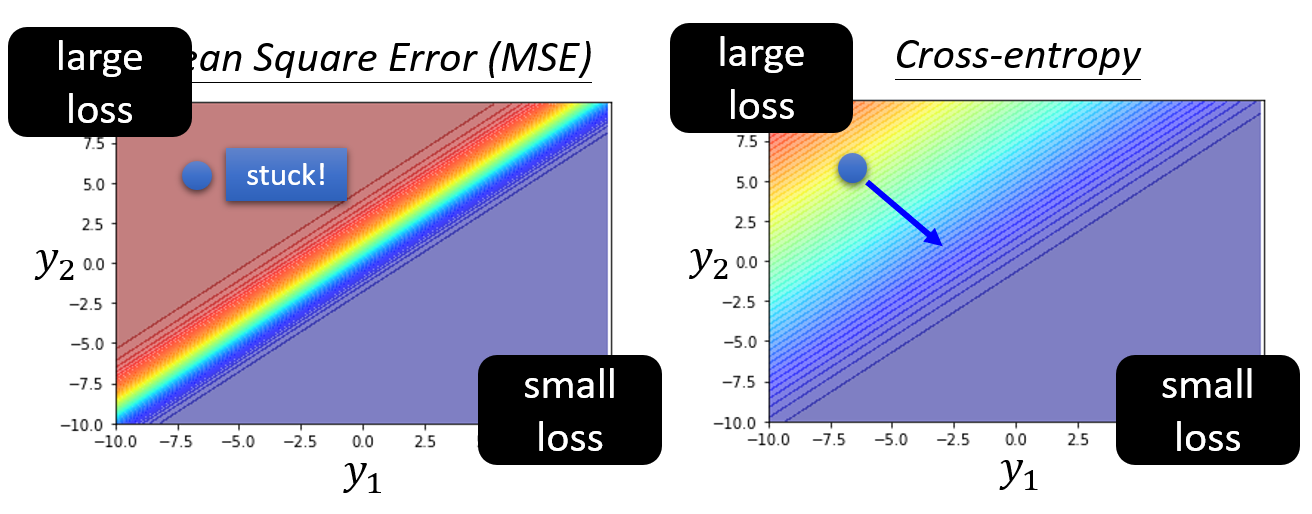
  可以看到：

  • 当 \(y_1\) 很大，\(y_2\) 很小的时候，两者得到的损失都很小；当 \(y_1\) 很小，\(y_2\) 很大的时候，两者得到的损失都很大
  • 然而，如果初始参数位于图上蓝点所示位置，并且使用一般的梯度下降法（即学习速率不变）的话，由于 MSE 的误差曲面过于平坦，即梯度很小，因此就会卡在原地不走了；而交叉熵的误差曲面较为陡峭，即有一定的梯度，因此可以继续走下去

  所以在分类模型中，交叉熵的计算方法更适用于优化过程。

Example: Pokémon/Digimon Classifier⚓︎

下面将以宝可梦 / 数码宝贝分类器为例，加深对机器学习原理的认识，同时也会学习到模型复杂度(model complexity) 对训练的影响。

Function with Unknown Parameters⚓︎

回顾一下训练的过程——第一步是基于我们的领域知识，去找一个带有未知参数的函数。这个函数大致长这样：

现在从宝可梦和数码宝贝中进行随机采样，观察它们的特征：

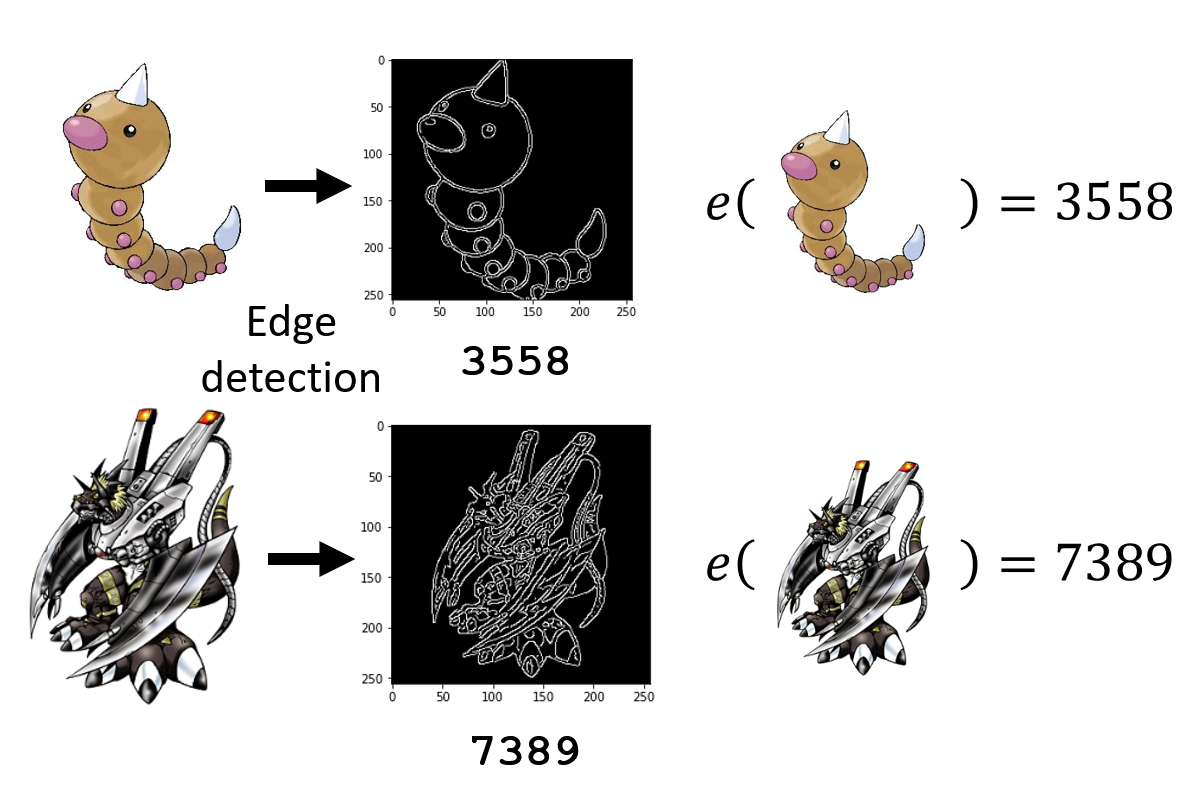
比对两者的画风，不难发现数码宝贝的线条较为复杂，而宝可梦的线条更为简单。为了验证这一发现的正确性，可以用一些图像处理工具来提取这些图片的线条：

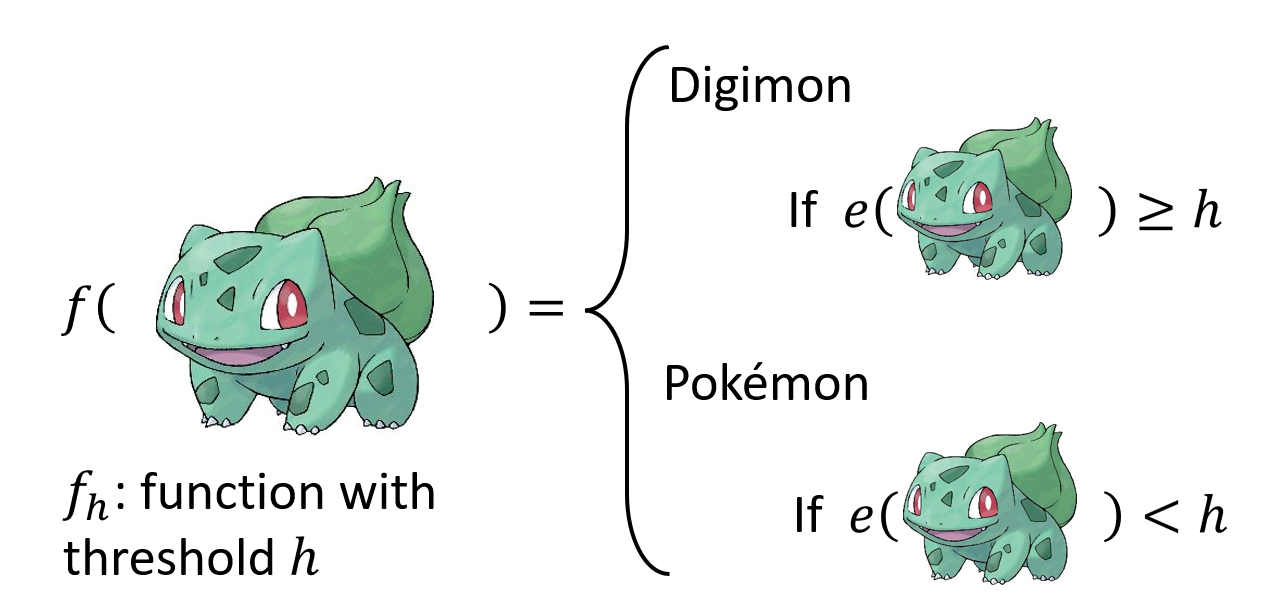
使用边缘检测工具后，可以得到中间的图片，其中白色的像素表示精灵的线条。很明显，上面的宝可梦的线条比下面的数码宝贝的线条少得多。根据这一发现，我们可以确定大致的函数形式为：

• 函数用 \(f_h\) 表示，其中 \(h\) 是一个阈值，作为划分宝可梦和数码宝贝的依据：当超过该阈值时，说明该图像表示的是数码宝贝，否则的话就是宝可梦
  • 并且假定阈值的取值范围为 \(H = \{1, 2, \dots, 10000\}\)（图片最多有 10000 个像素点），因此 \(|H|\) 可以表示候选函数的个数，即模型的“复杂度”(model "complexity")
• 另外用函数 \(e\) 表示边缘检测工具计算得到的线条像素数

Loss of a Function⚓︎

接下来进入训练的第二步：对于给定的数据，定义一个损失函数。

• 假如给定一个数据集 \(D = \{(x^1, \hat{y}^1), (x^2, \hat{y}^2), \dots, (x^N, \hat{y}^N)\}\)，其中 \(x^n\) 表示输入的图片，\(y^n\) 表示输出的宝可梦 / 数码宝贝的选项

• 此时损失函数是一个关于阈值 \(h\) 和数据集 \(D\) 的函数，即：

  \[ L(h, D) = \dfrac{1}{N} \sum\limits_{n=1}^N l(h, x^n, \hat{y}^n) \]
  • 每个数据的损失（或者说误差）可以用一个简单的函数计算：\(I(f_h(x^n) \ne \hat{y}^n) = \begin{cases}1 & \text{If } f_h(x^n) \ne \hat{y}^n \\ 0 & \text{Otherwise}\end{cases}\)
  • 那么损失函数的取值范围为 \([0, 1]\)，因此这里的损失函数又称为错误率(error rate)
  • 当然，由于这是一个分类问题，所以也可以用交叉熵来计算误差。但为了方便后续的解释，而且这是一个二项分类问题，所以后面还是按照这里定义的误差函数来分析

如果我们能够收集世界上所有的宝可梦和数码宝贝，由此构建了一个数据集 \(\textcolor{red}{D_{all}}\)，那么就能从中找出最佳的阈值 \(\textcolor{red}{h^{all}}\)，即 \(\textcolor{red}{h^{all}} = arg \min\limits_h L(h, \textcolor{red}{D_{all}})\)。然而，事实上我们只能从 \(\textcolor{red}{D_{all}}\) 中收集部分的例子 \(\textcolor{cornflowerblue}{D_{train}} = \{(x^1, \hat{y}^1), (x^2, \hat{y}^2), \dots, (x^N, \hat{y}^N)\}\)，其中 \(\{x^n, \hat{y}^n\} \sim \textcolor{red}{D_{all}}\) 是独立同分布的 (i.i.d.)；而从 \(\textcolor{cornflowerblue}{D_{train}}\) 上得到阈值为 \(\textcolor{cornflowerblue}{h^{train}} = arg \min\limits_{h} L(h, \textcolor{cornflowerblue}{D_{train}})\)。

所以，\(\textcolor{red}{h^{all}}\) 只是我们的理想，但现实是我们只能通过机器学习得到 \(\textcolor{cornflowerblue}{h^{train}}\)（理想很丰满，现实很骨感（悲））。因此，机器学习的目标就是要让现实尽可能地接近理想，在这个例子中就是要让 \(L(\textcolor{cornflowerblue}{h^{train}}, \textcolor{red}{D_{all}})\) 与 \(L(\textcolor{red}{h^{all}}, \textcolor{red}{D_{all}})\) 尽可能地接近。下面通过一个例子来加深对“理想和现实”的认识：

例子

理想现实 1 现实 2

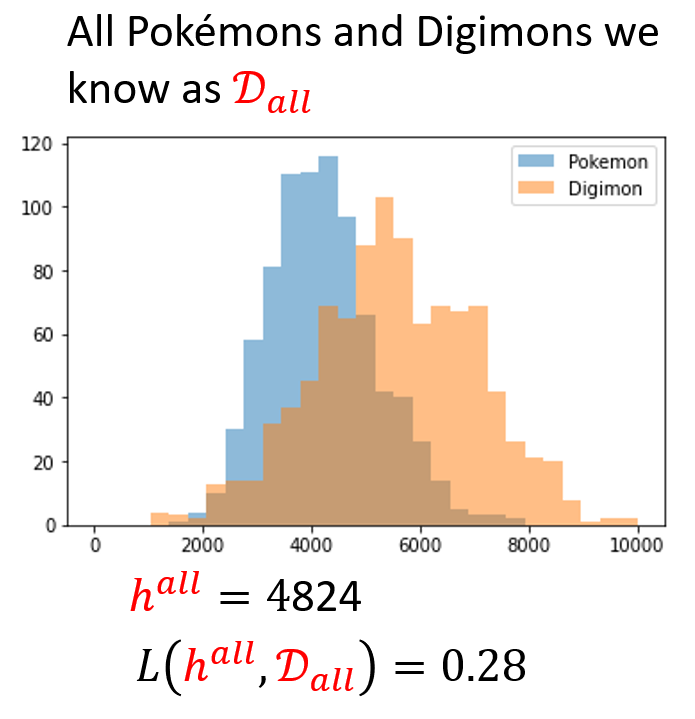
假设我们收集到了世界上所有的宝可梦和数码宝贝。下面给出了相应的数据分布图，并计算了最佳阈值及其损失：

注意

要清楚实际上是不可能获得所有数据的，这里只是一个假设。在现实中，一般会用测试数据 \(D_{test}\) 作为 \(D_{all}\) 的代表，因为 \(D_{test}\) 可以反映 \(D_{all}\) 的数据特征。

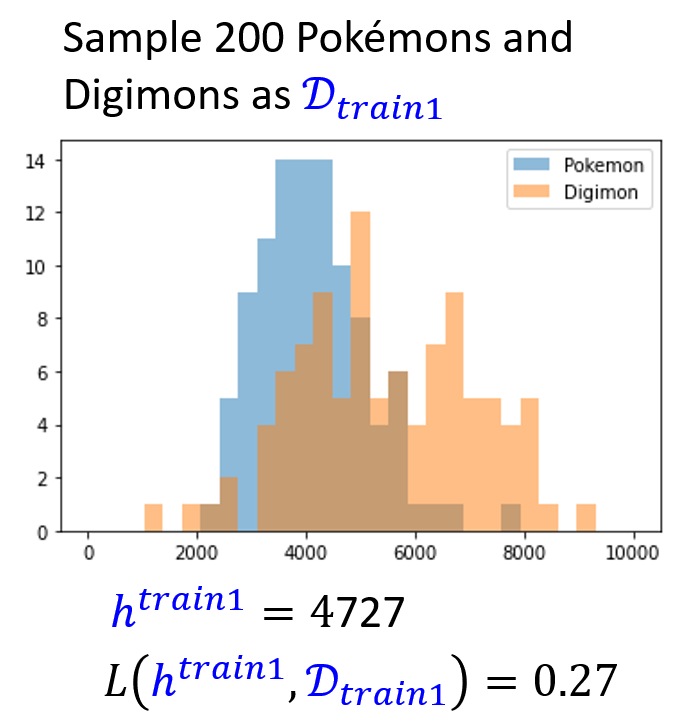
现在随机采样得到 200 只宝可梦和数码宝贝，得到以下数据分布图，并计算了最佳阈值及其损失：

思考

诶，怎么 \(L(\textcolor{cornflowerblue}{h^{train1}}, \textcolor{cornflowerblue}{D_{train1}})\) 比 \(L(\textcolor{red}{h^{all}}, \textcolor{red}{D_{all}})\) 还要低呢？事实上，这样的比较是没有意义的，因为这两个损失值是根据不同的数据集计算得到的，两者没有可比性。

我们应该关注的是 \(L(\textcolor{cornflowerblue}{h^{train1}}, \textcolor{red}{D_{all}})\) 的值。在这个例子中，其值为 0.28，与 \(L(\textcolor{red}{h^{all}}, \textcolor{red}{D_{all}})\) 一致，这说明了“现实与理想”近乎一样 ~

然而，这只是最理想的情况，后面的“现实”可没有这么“理想”！

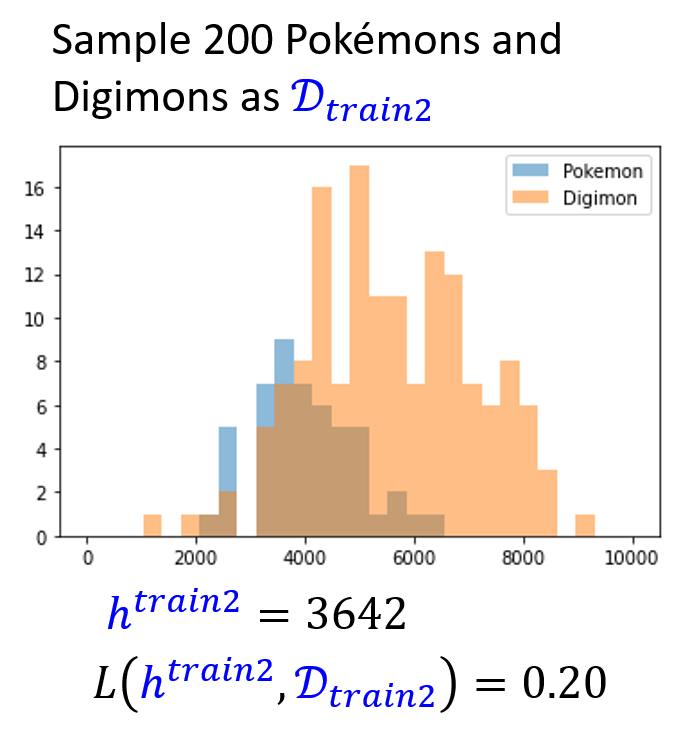
现在另外随机采样得到 200 只宝可梦和数码宝贝，得到以下数据分布图，并计算了最佳阈值及其损失：

通过前面的分析，我们知道即使 \(L(\textcolor{cornflowerblue}{h^{train2}}, \textcolor{cornflowerblue}{D_{train2}})\) 再小也无济于事，效果好不好还得看 \(L(\textcolor{cornflowerblue}{h^{train2}}, \textcolor{red}{D_{all}})\)——其结果为 0.37，比 \(L(\textcolor{red}{h^{all}}, \textcolor{red}{D_{all}})\) 大好多，这说明了本次训练的效果比较糟糕。

下面从定量的角度分析训练的目标——我们希望 \(L(\textcolor{cornflowerblue}{h^{train}}, \textcolor{red}{D_{all}}) - L(\textcolor{red}{h^{all}}, \textcolor{red}{D_{all}}) \le \delta\)，其中 \(\delta\) 是我们人为设定的范围——如果希望理想和现实很接近，那么就调小这个值。接下来就要考虑什么样的 \(\textcolor{cornflowerblue}{D_{train}}\) 能够满足这一不等式的要求呢？这里直接给出结论：

当这一不等式满足时，我们希望的不等式条件就能成立。此时在对任意 \(\textcolor{green}{h}\) 求解损失 \(L\) 时，这个 \(\textcolor{cornflowerblue}{D_{train}}\) 是 \(\textcolor{red}{D_{all}}\) 的一个不错的代表。

更一般地，我们希望采样得到一个好的数据集 \(\textcolor{cornflowerblue}{D_{train}}\)，满足：

那么我们便想知道采样到一个坏的数据集 \(\textcolor{cornflowerblue}{D_{train}}\) 的概率是多少，下面就来讨论这一问题

Probability of Failure⚓︎

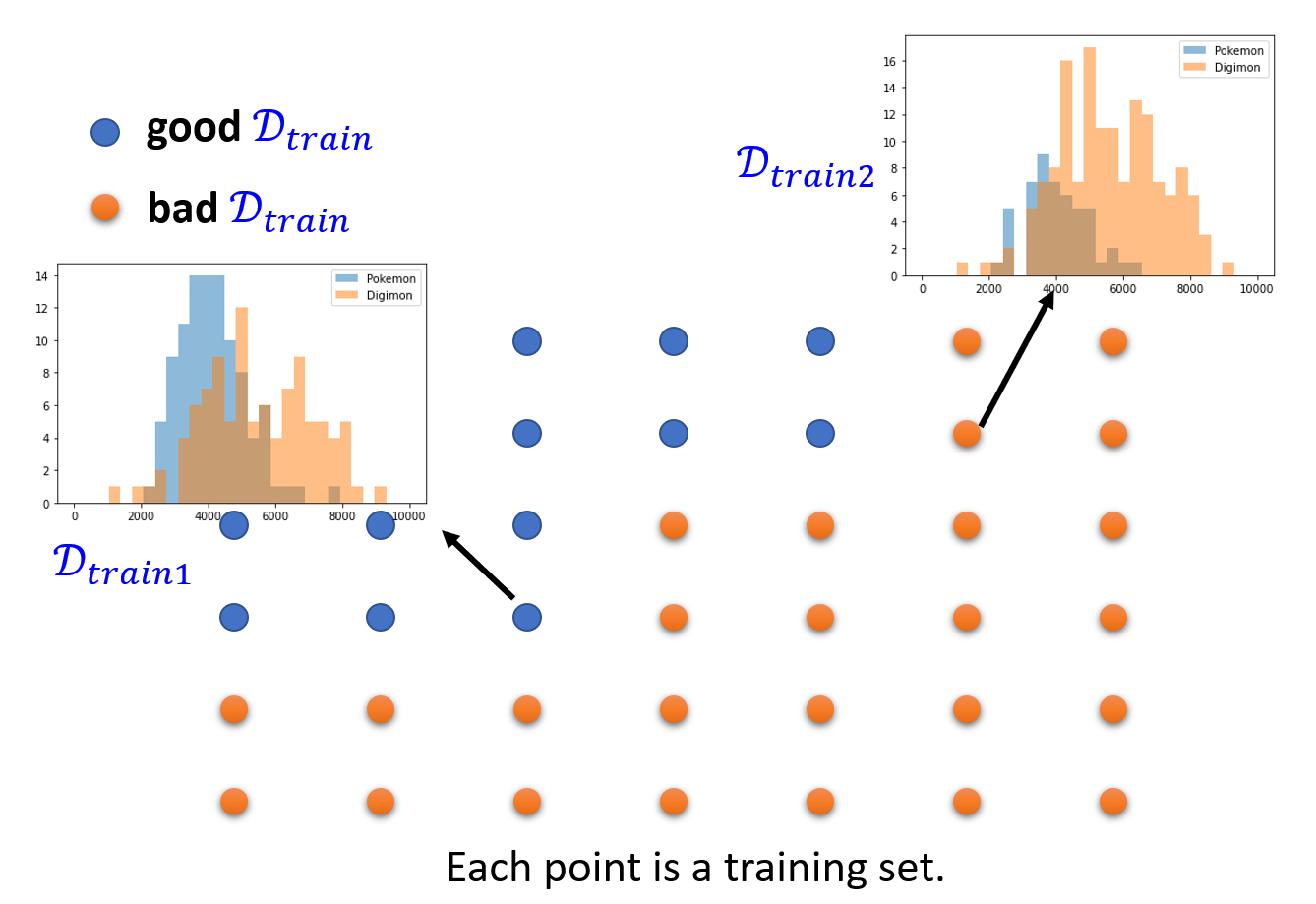
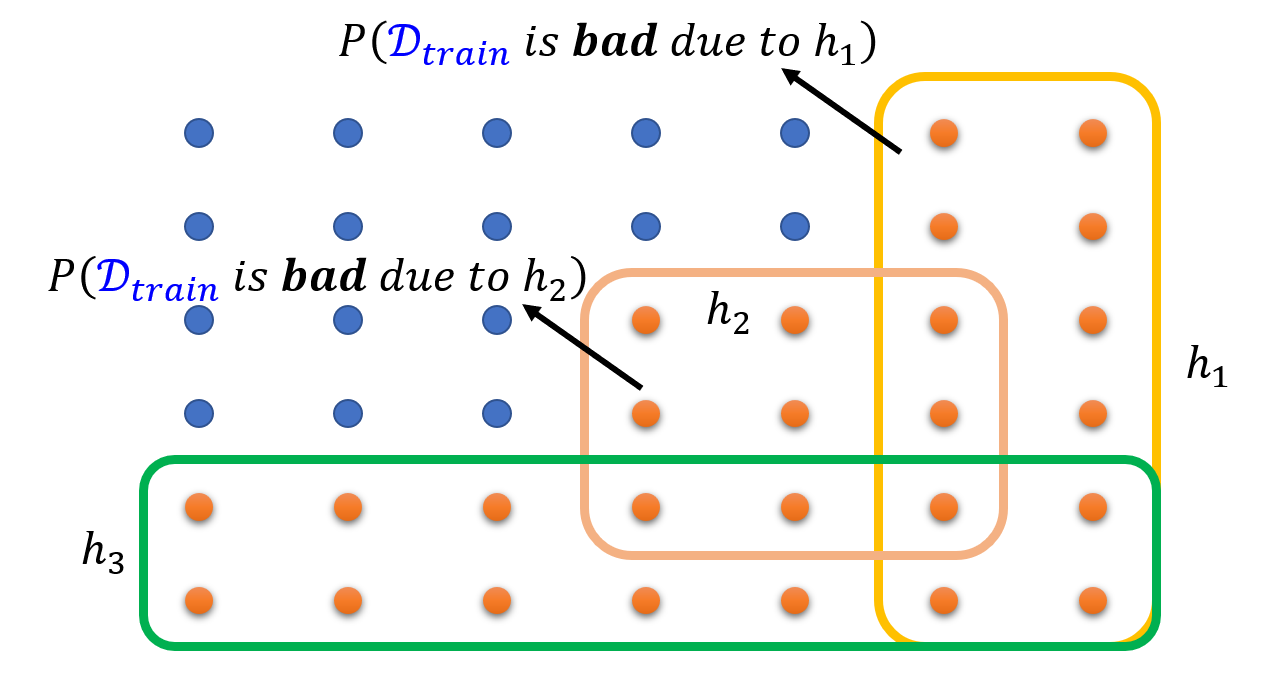
假设我们随机采样多次，得到多组如下所示的训练数据集。其中用蓝色的点表示好的数据集，黄色的点表示坏的数据集。那么黄色点的数量占所有点的数量就是采样到坏的数据集的概率 \(P(\textcolor{cornflowerblue}{D_{train}}\ is\ \bm{bad})\)。

如果 \(\textcolor{cornflowerblue}{D_{train}}\) 是坏的话，那么至少有一个阈值 \(\textcolor{green}{h}\)，使得 \(\forall \textcolor{green}{h} \in H, |L(\textcolor{green}{h}, \textcolor{cornflowerblue}{D_{train}}) - L(\textcolor{green}{h}, \textcolor{red}{D_{all}})| > \varepsilon\)。下图展示了其中一种可能的情况：

用数学语言描述为：

• 为了计算方便，我们将集合的并运算转化为求和公式。这一放缩比较大胆，因为求和的结果很可能超过 1，但为了后续讲解的方便，所以就不再深究这个问题了

• 下面用数学公式和一些图形来回顾何为“\(\textcolor{cornflowerblue}{D_{train}}\ is\ \bm{bad}\ due\ to\ \textcolor{green}{h}\)”

  

• 用霍夫丁不等式计算这个概率值：

  \[ P(\textcolor{cornflowerblue}{D_{train}}\ is\ \bm{bad}\ due\ to\ \textcolor{green}{h}) \le 2exp(-2N \varepsilon^2) \]
  • 该不等式要求损失值 \(L \in [0, 1]\)
  • \(N\) 表示 \(\textcolor{cornflowerblue}{D_{train}}\) 中的样例数

继续化简式子：

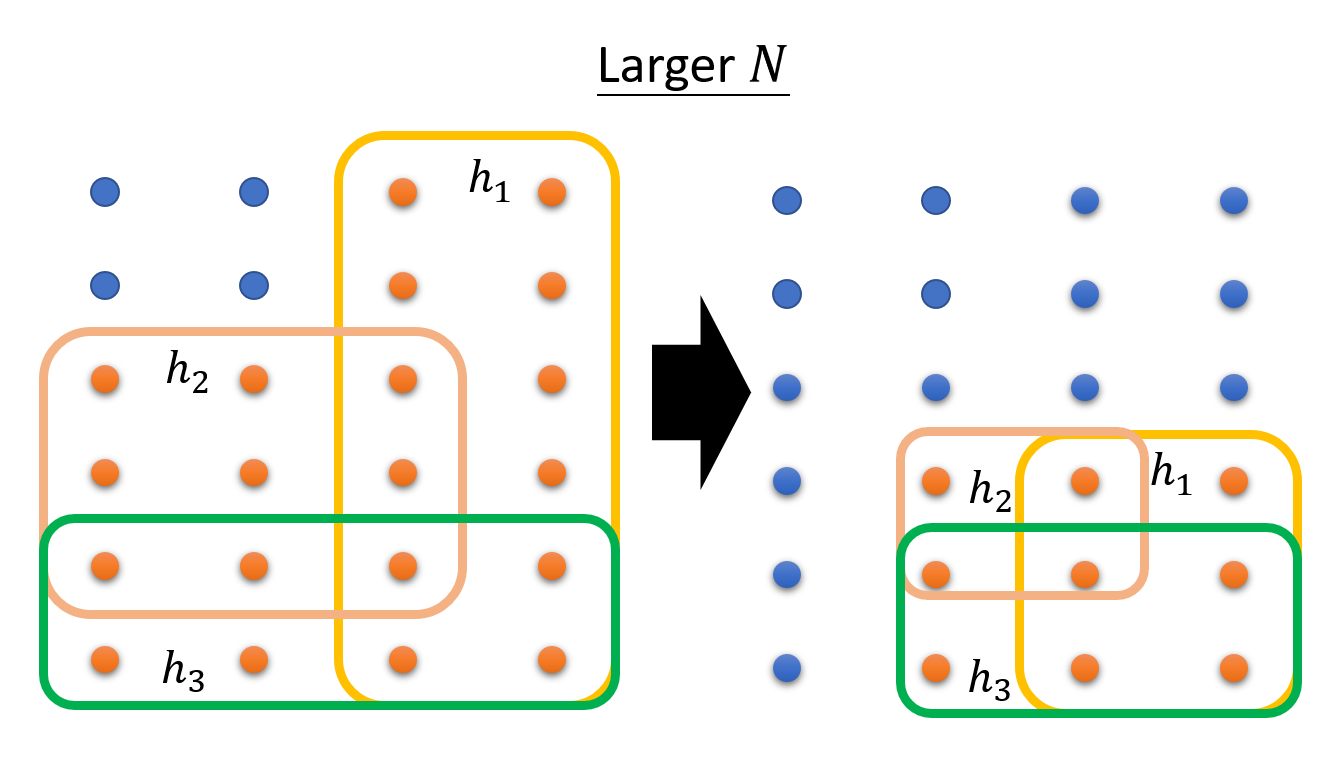
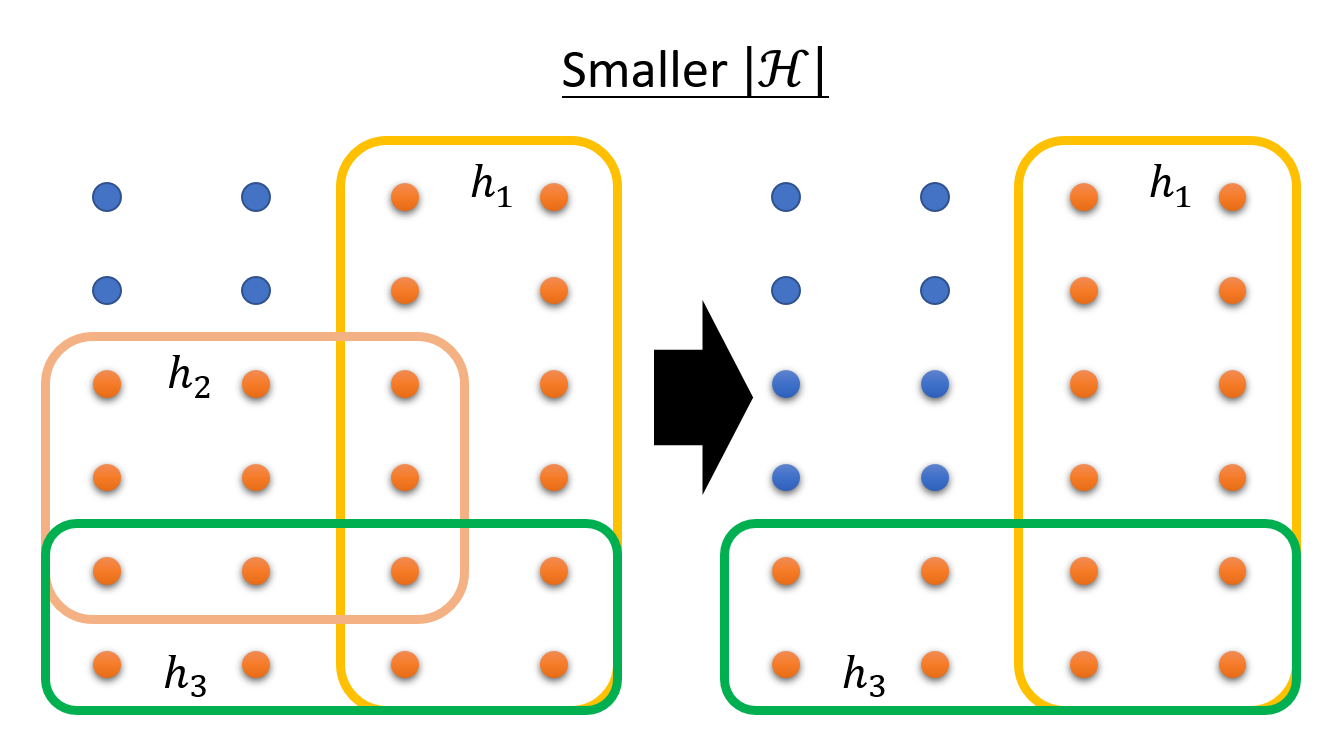
很明显，要想减小概率 \(P(\textcolor{cornflowerblue}{D_{train}}\ is\ \bm{bad})\)，可以做的调整有：

• 增大 \(N\)

  

• 减小 \(|H|\)

  

例子

如果我们希望 \(P(\textcolor{cornflowerblue}{D_{train}}\ is\ \bm{bad}) \le \delta\)，需要多少的训练样本呢？

\[ |H| \cdot 2exp(-2N\varepsilon^2) \le \delta \Rightarrow N \ge \dfrac{\log(\frac{2|H|}{\delta})}{2\varepsilon} \]

假设 \(|H| = 10000, \delta = 0.1, \varepsilon = 0.1\)，可以解得 \(N \ge 610\)

Model Complexity⚓︎

再次观察霍夫丁不等式：其中的 \(|H|\) 表示可选的函数个数。然而，可能会出现一种情况：函数的参数是连续的，那么 \(|H|\) 不就是 \(\infty\) 了吗，此时上面的不等式也就没有用了。关于这个问题，有以下几种解答：

• 计算机能做的事情都是离散的（好像很有道理）
• 使用 VC-dimension（本笔记中不会涉及到）

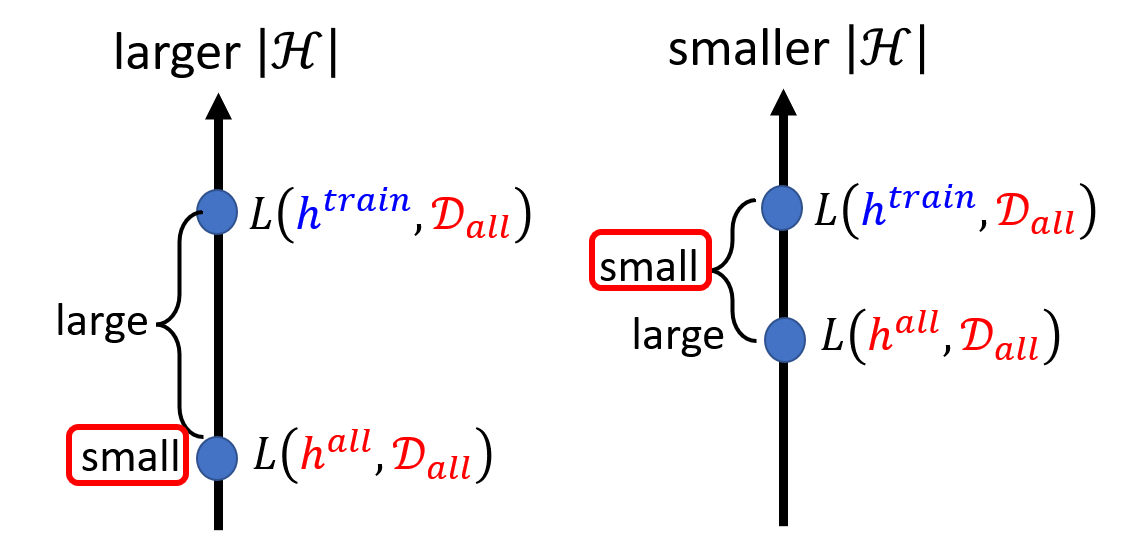
既然可以通过减小 \(|H|\) 来降低 \(P(\textcolor{cornflowerblue}{D_{train}})\)，但为什么实际上我们不会让 \(|H|\) 变得很小？原因在于：更小的 \(H\) 意味着更少的候选函数（模型），那么 \(\textcolor{red}{h^{all}} = arg \min\limits_{h \in H} L(h, D_{all})\) 的变动余地也很小，这可能导致 \(L(\textcolor{red}{h^{all}}, \textcolor{red}{D_{all}})\) 变得更大。此时让 \(L(\textcolor{cornflowerblue}{h^{train}}, \textcolor{red}{D_{all}})\) 再接近 \(L(\textcolor{red}{h^{all}}, \textcolor{red}{D_{all}})\)，前者的值会跟着后者的值一起变得很大，那么训练效果就不是很好了。下图形象地说明这一问题：

那么，是否存在一种“鱼和熊掌可以兼得”的方法呢？答案便是下一节介绍的深度学习(deep learning)！