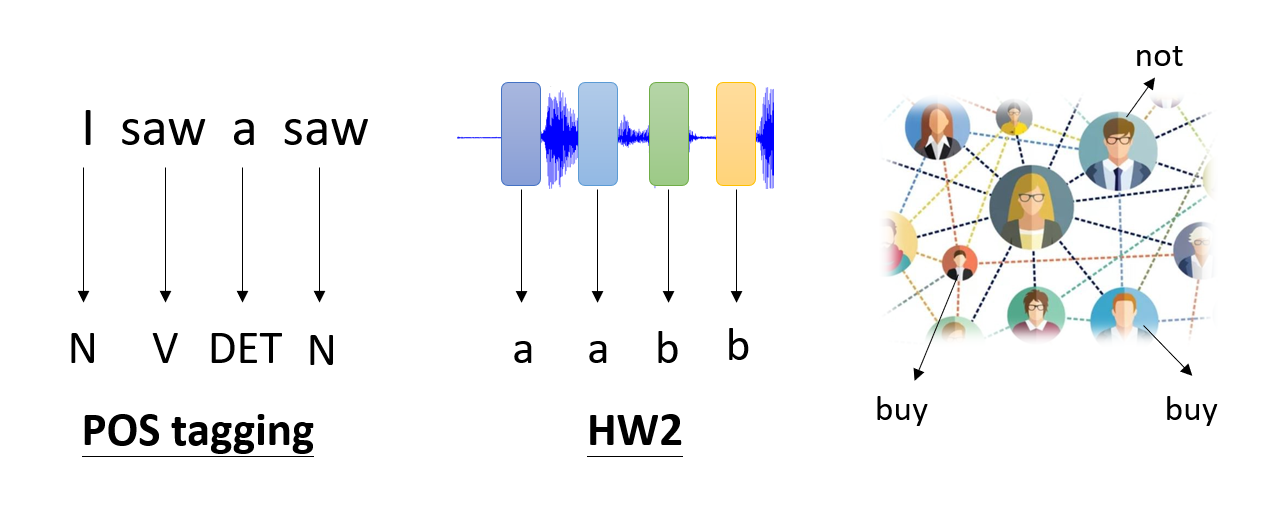
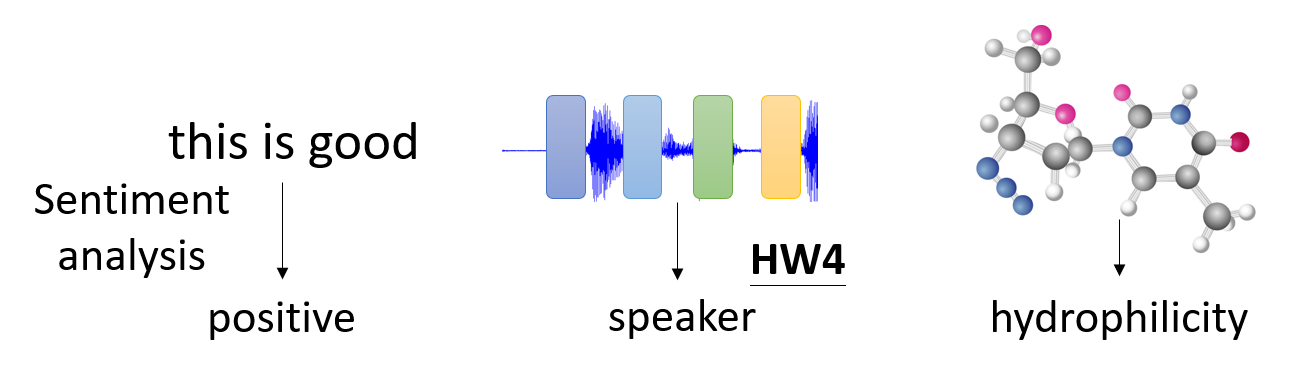
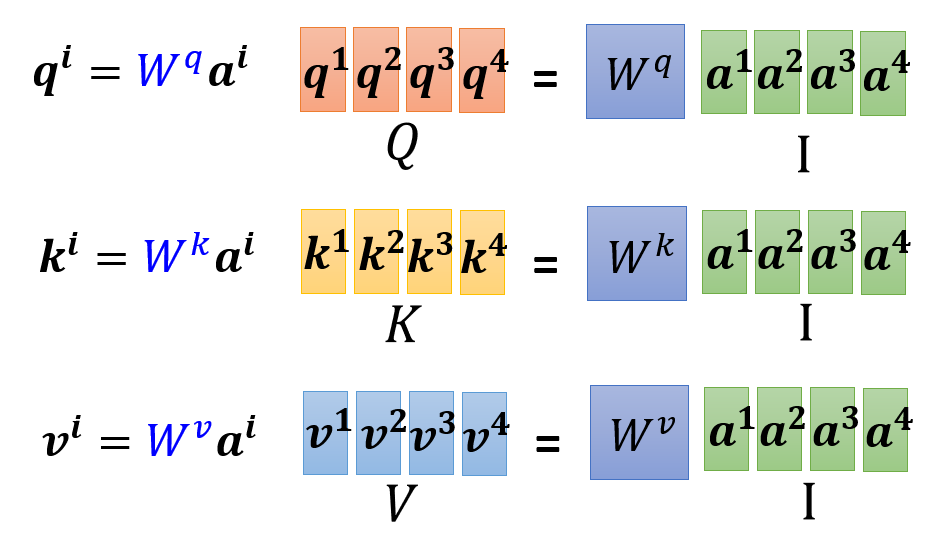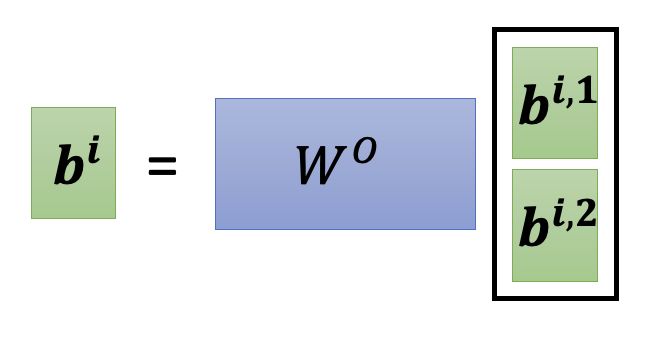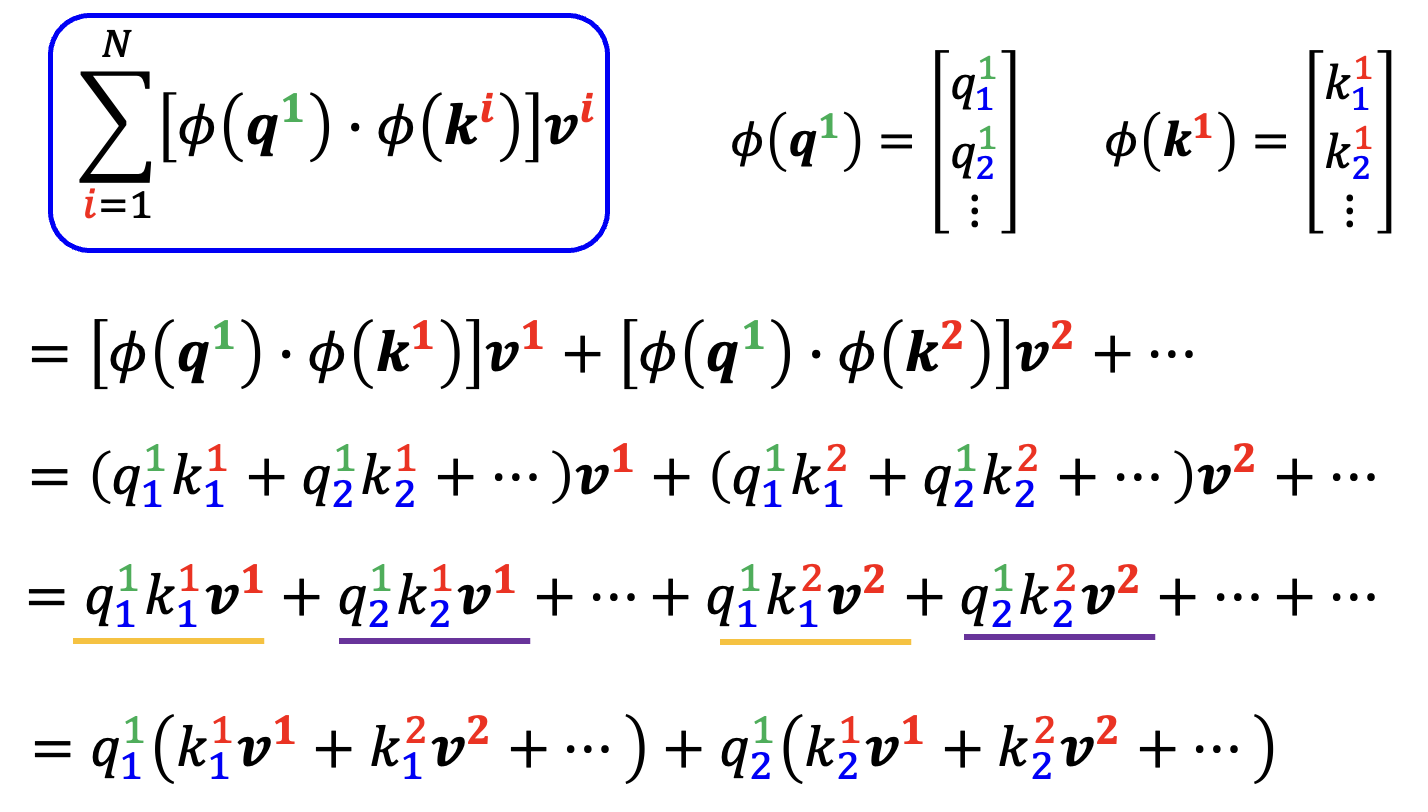Self-Attention⚓︎
约 6118 个字 预计阅读时间 31 分钟
之前我们介绍的模型,都只是将一个向量作为输入(比如 COVID-19 感染人数预测、图像处理等问题
Inputs and Outputs⚓︎
首先需要考虑的一个问题是:如何将实际问题的输入转化为一组向量的形式呢?来看下面几个例子:
例子
一个句子就是一个向量序列,而句子中的每个单词对应一个个的向量。将单词转化为向量的方式有:
-
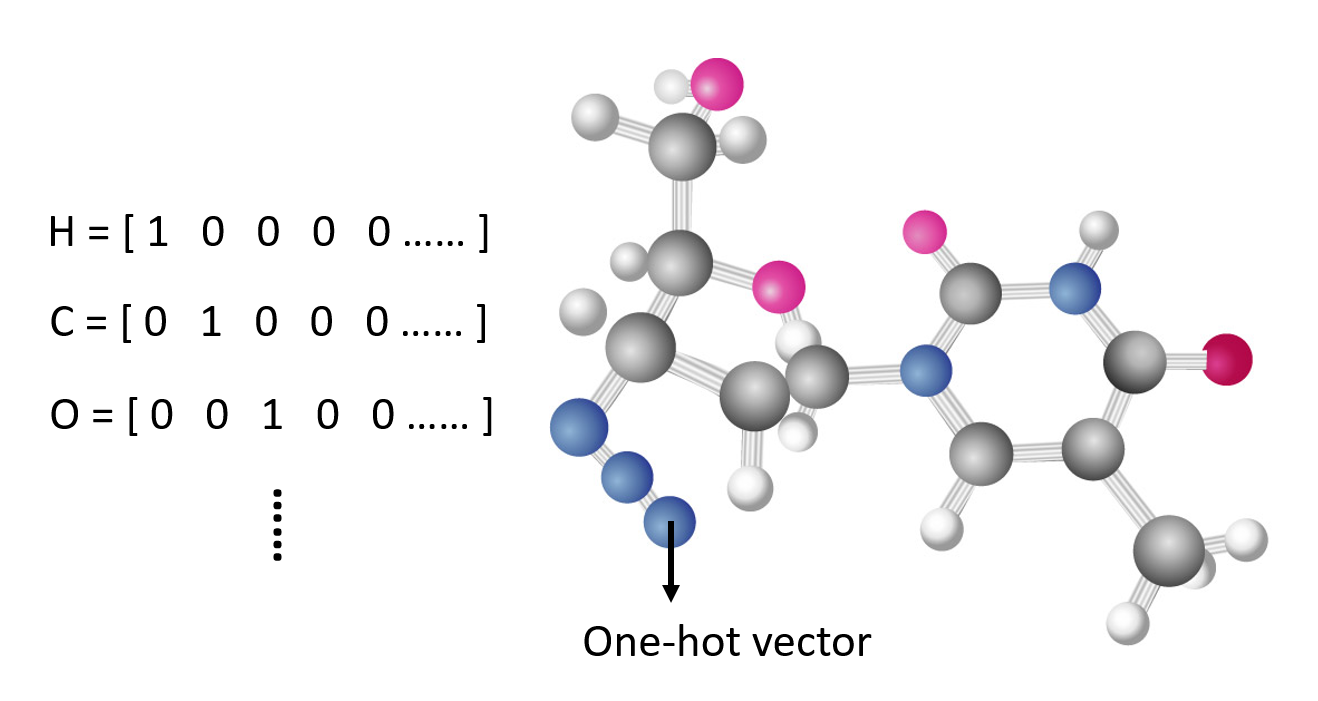
独热编码(one-hot encoding):假如所有单词的个数为 n,那么我们就用一个大小为 n 的向量来表示每个单词,每个位置上的元素表示唯一的单词
-
这种方式简单粗暴,但是不仅占用内存空间大,而且无法体现出两个单词之间的联系,即没有考虑到语义信息
-
-
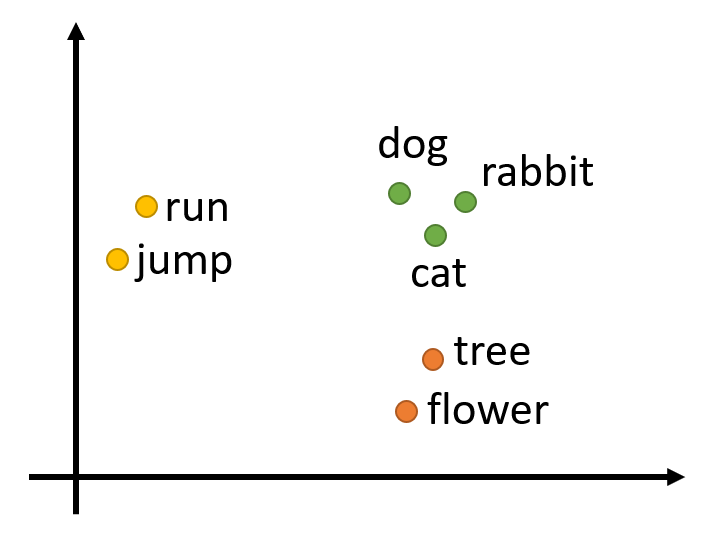
词嵌入(word embedding):语义关系越接近的两个单词,它们对应的向量值会更加接近,如下图所示:
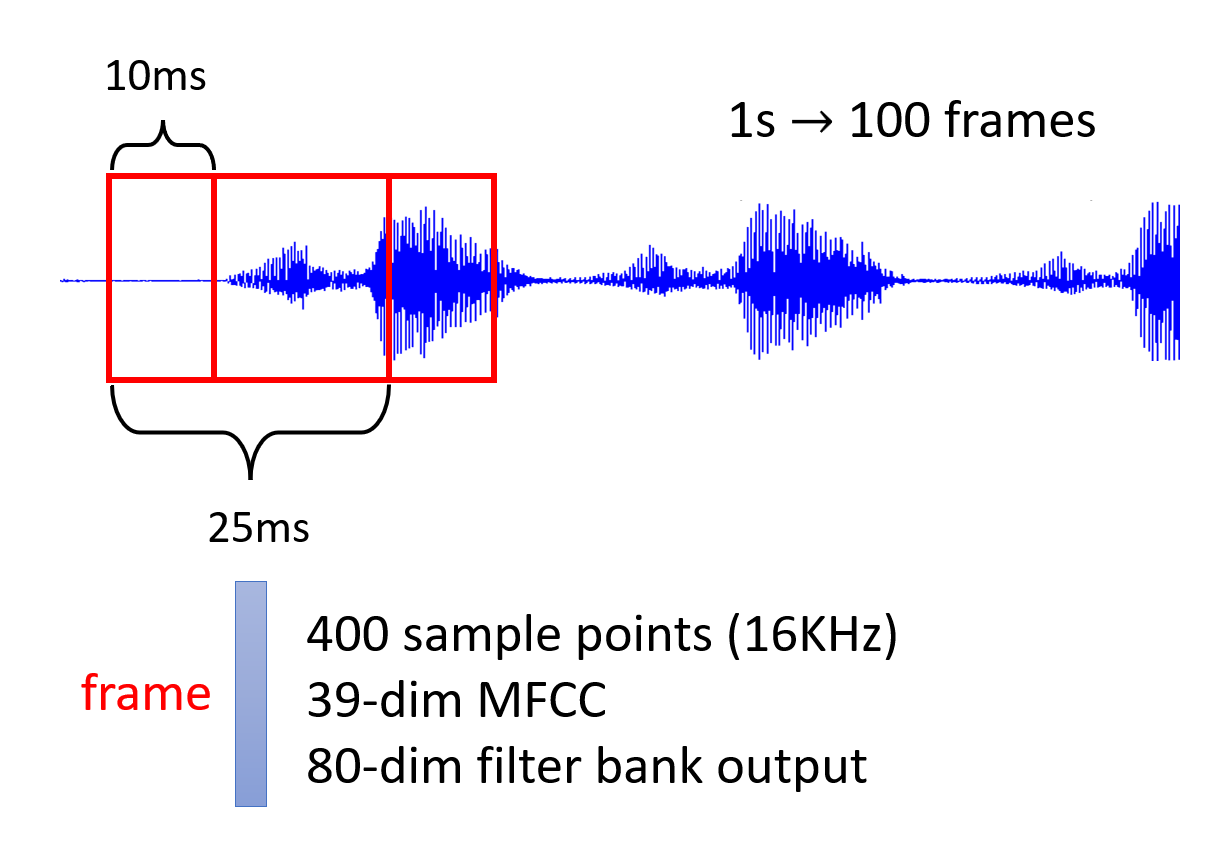
在机器学习课程 HW2 中,我们将语音看作一段段的帧(25ms 的语音
而输出的内容则可以分为以下几种情况:
-
每个输入向量对应一个输出标签 (label)(即预测值)
-
对于整组向量,输出一个标签
-
由模型决定输出标签的数量(seq2seq,序列到序列)
不过之后我们只专注第一种输出情况,即对于 N 个向量的输入,输出相应的 N 个标量或类。
Self-Attention⚓︎
接下来考虑如何构建适用于向量序列输入的模型。
Naive Idea
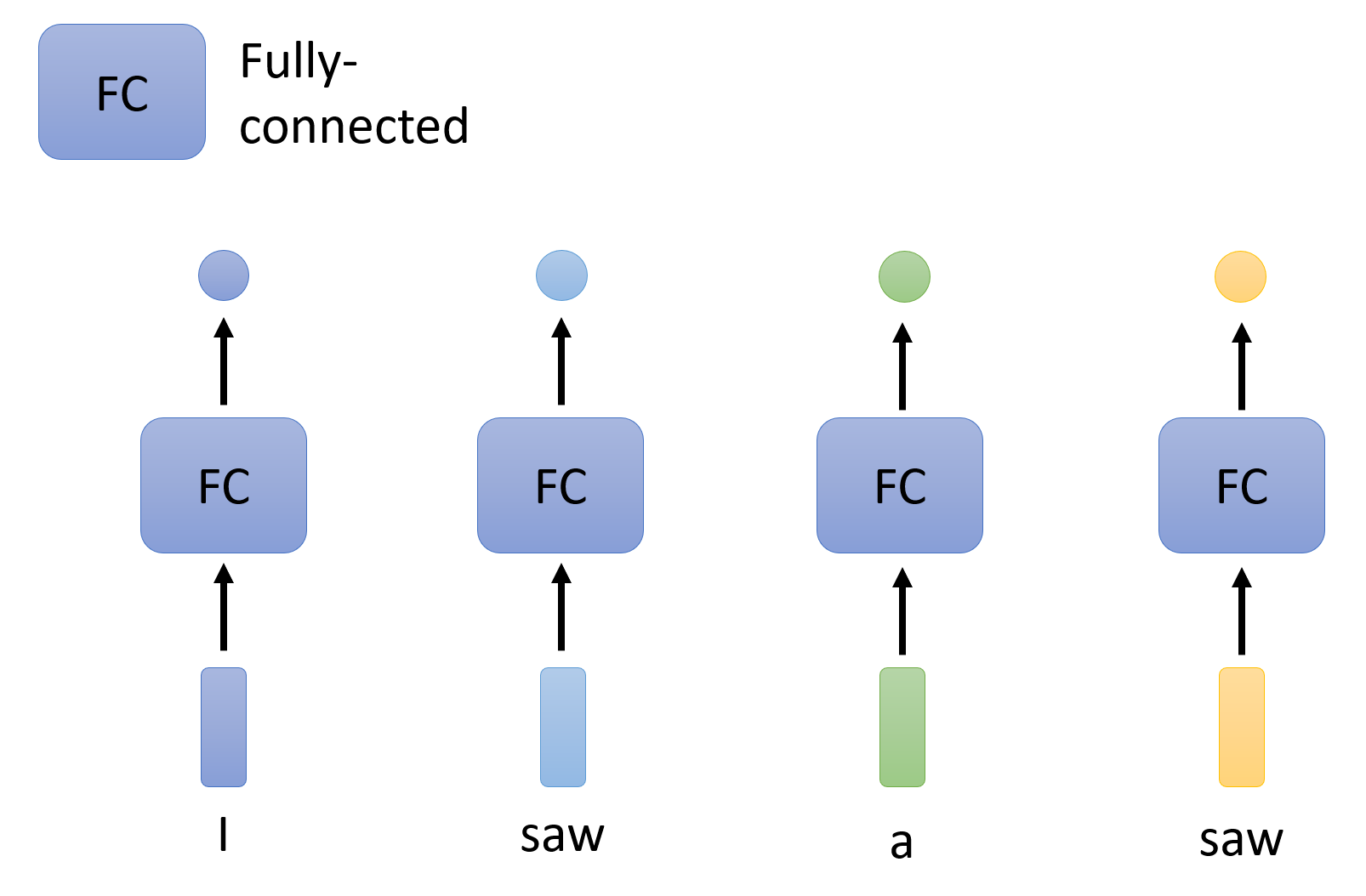
既然 N 个向量输入对应 N 个输出,那么不妨让每个向量单独进入一个全连接层得到一个输出,如下图所示:
显然,这样有一个很大的缺陷:我们没有考虑到向量序列各个向量之间的联系,各个向量都是“各自为政”的。所以,如果有两个向量的值是相等的,那就会被视为意义相同的两个东西,从而产生两个相同的输出。
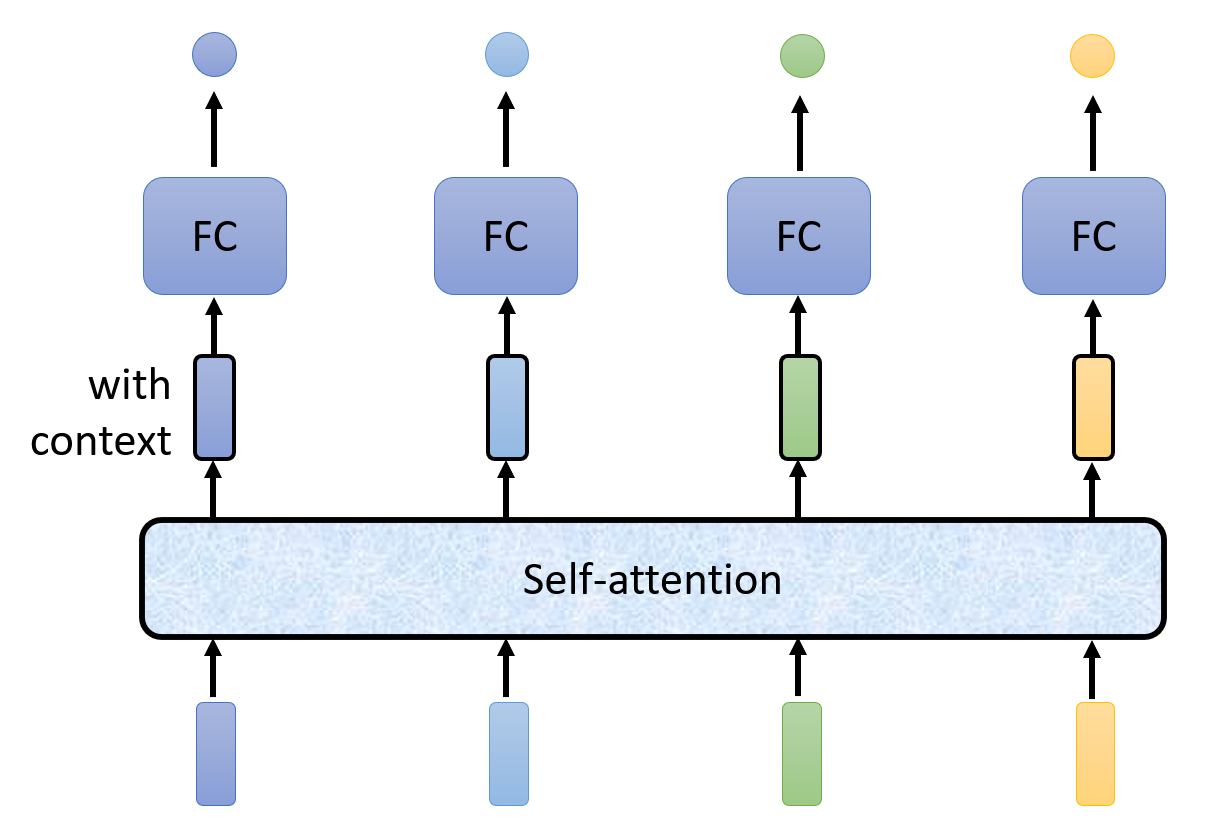
每个向量输入都有一个对应的全连接层,这个全连接层不仅应该接收对应的向量输入,同时也要顾及整个上下文(context) 中的向量。
-
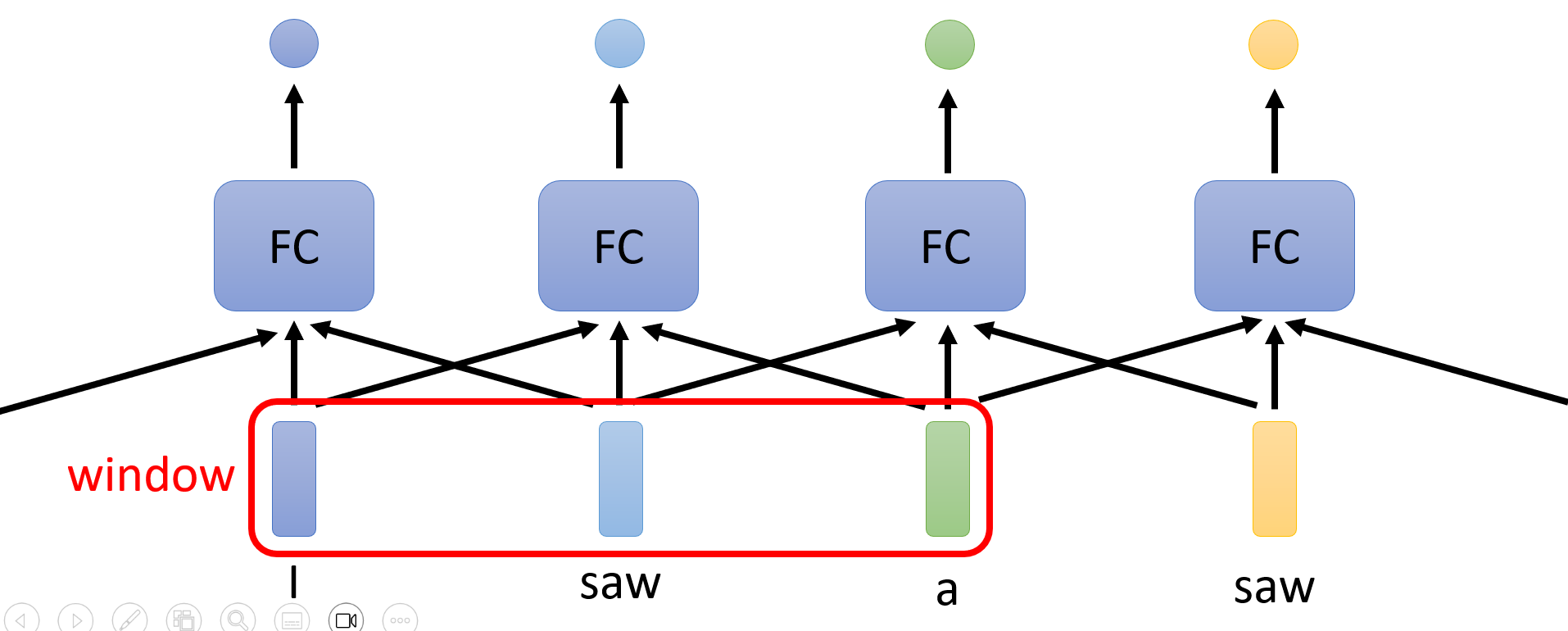
这个上下文的范围可以是一个局部的窗口,这样就仅考虑与对应输入向量相邻的部分向量
-
也可以将整个向量序列都纳入考虑范围内,这样考虑得更全面些,比如用一个固定大小的窗口覆盖整个向量序列
- 但是向量序列的长度可长可短,所以不能简单地使用窗口来实现这一点
- 再说,就算有一个足够大小的窗口可以容纳所有向量,但是这样也意味着全连接层需要非常多的参数(\(n\) 个向量就会产生 \(n^2\) 个参数
) ,而过多的参数意味着很容易出现过拟合的问题
因此,这里引入一种更好的做法——使用一种名为“自注意”(self-attention) 的机制:
- 将输入向量送入全连接层之前,先让这些向量经过一种“自注意”的运算。对于每个输入向量,经过“自注意”运算后都会得到一个对应的输出,我们可以把这个输出看作是包含整个向量序列上下文信息的新向量,但同时也保留了原来输入向量的特征。
- 然后将这个新向量传给全连接层进行训练
这一过程如下图所示:
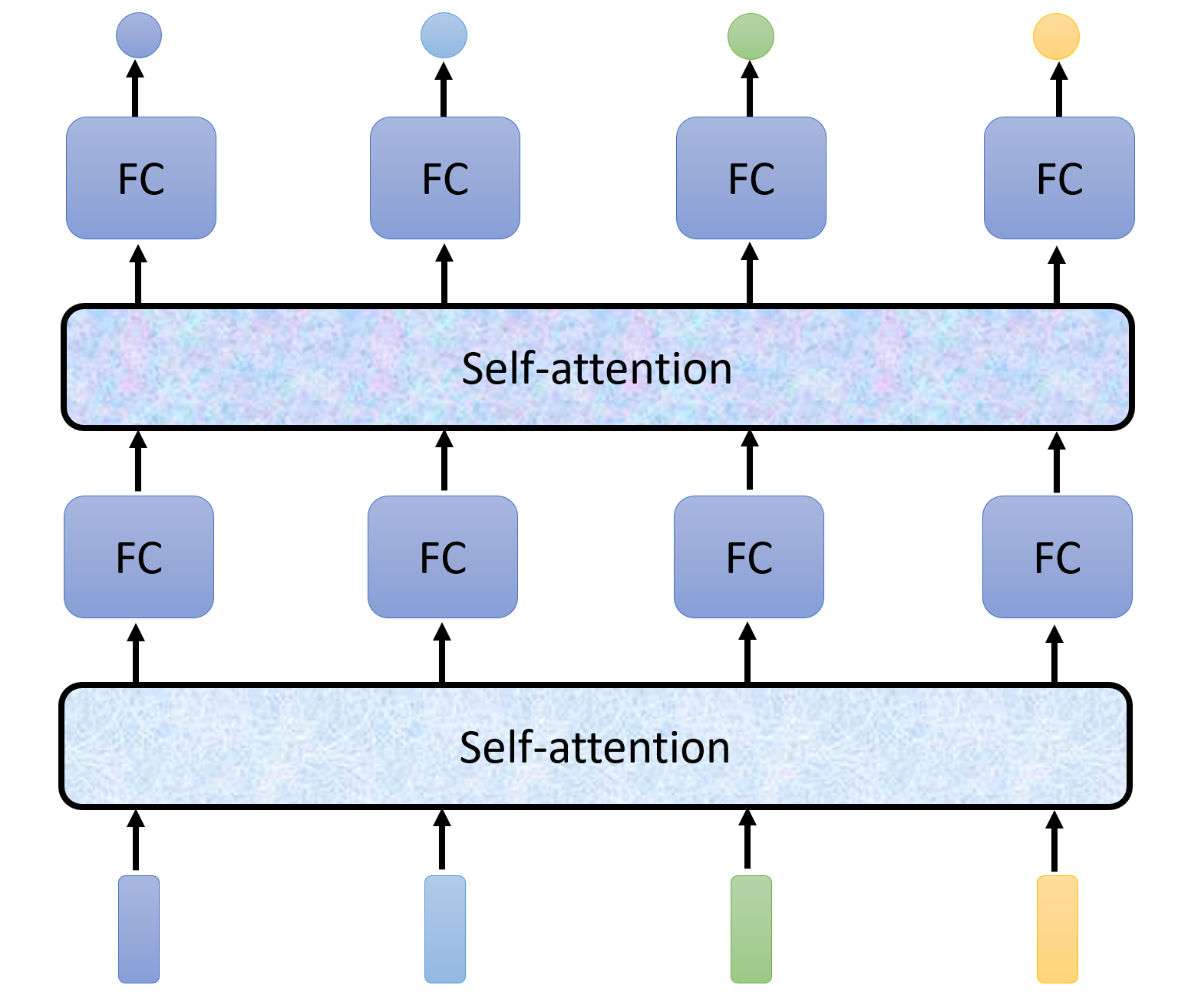
当然,在多层神经网络中,可以在每两个隐藏层之间塞一个自注意计算:
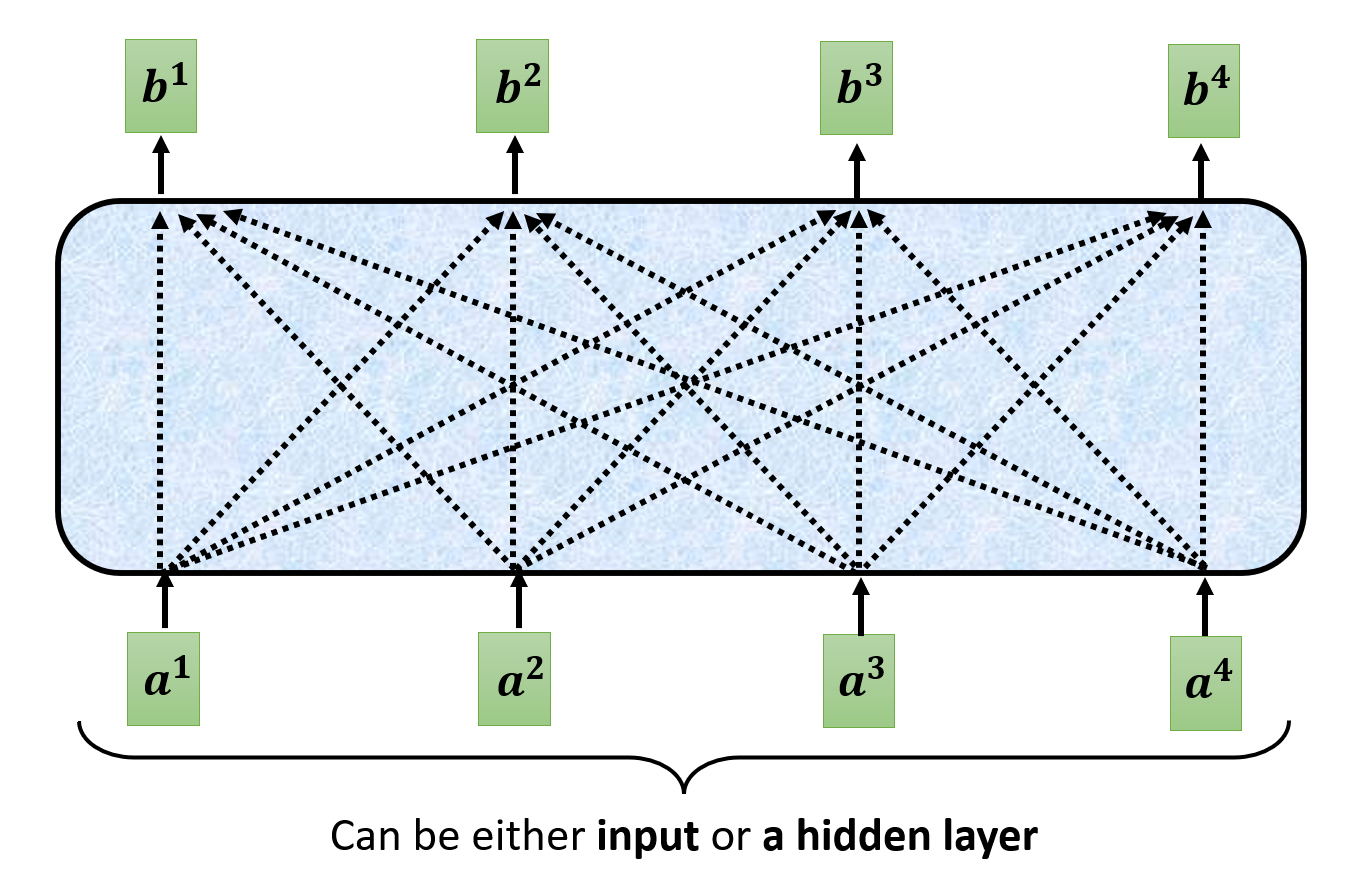
在自注意计算这个“盒子”的内部,输入和输出的关系如下所示:
其中输入既可以是最外面的向量序列,也可以是经过几层训练后得到的输出向量序列。现在我们就考虑某一个输出向量,比如 \(\bm{b^1}\),来认识一下自注意的计算过程。
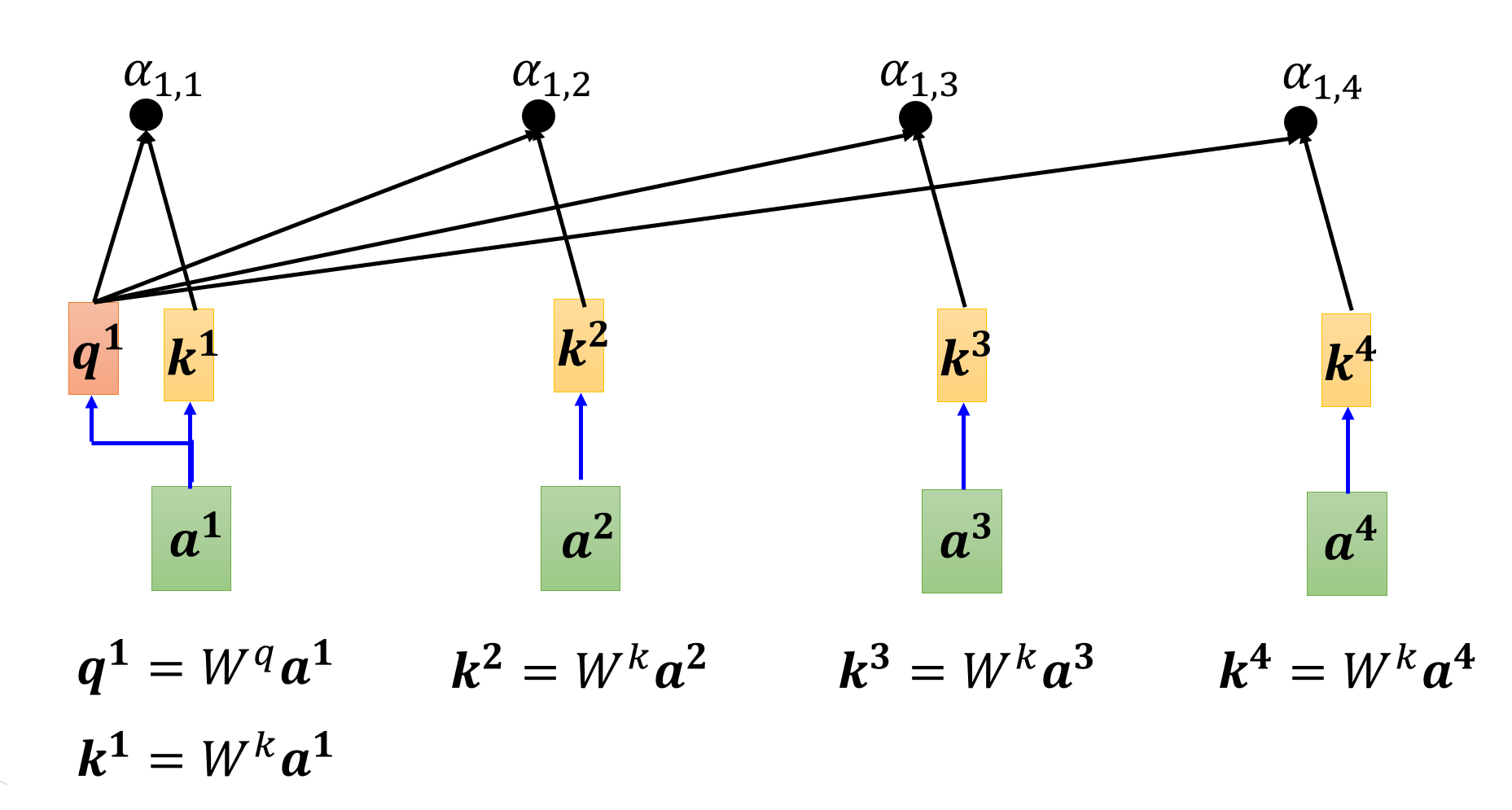
首先,我们要计算 \(\bm{b^1}\) 对应的输入向量 \(\bm{a^1}\) 与其他输入向量的相关程度(用 \(\alpha\) 表示
注
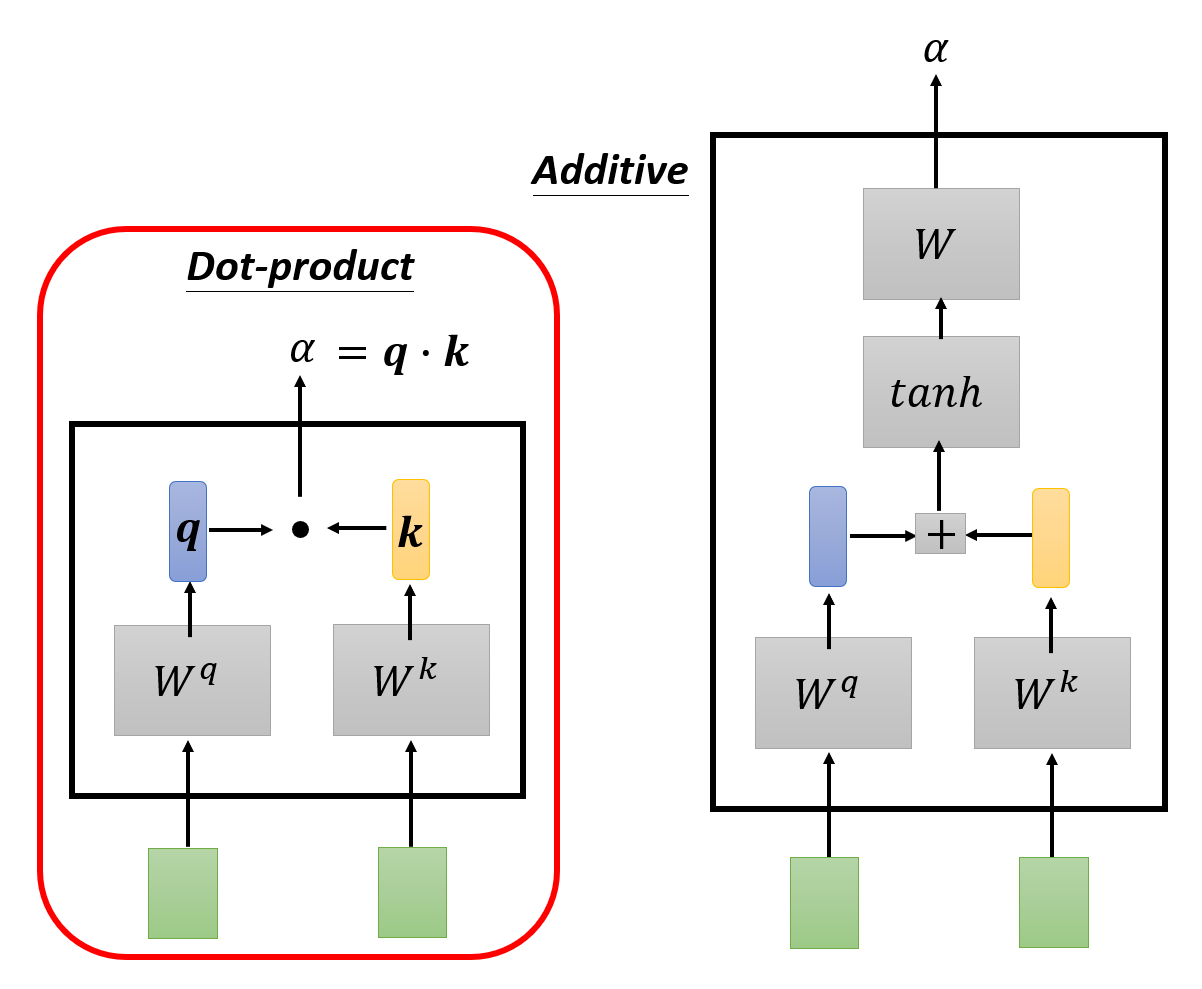
下面我们会将主要考虑的输入向量称为查询(query),而把另外的向量看作键(key),所以它们分别对应的矩阵为 \(W^q\) 和 \(W^k\),与矩阵相乘的结果分别为 \(\bm{q}\) 和 \(\bm{k}\)。
- 点积(dot-product):相关程度 \(\alpha = \bm{q} \cdot \bm{k}\)(向量的点积,得到一个标量)
- 加法 (additive):将 \(\bm{q} + \bm{k}\) 的结果丢给 \(\tanh\) 函数计算,然后再经过一次转换(用矩阵 \(W\) 表示)得到 \(\alpha\)
下面我们仅考虑点积这一方法。
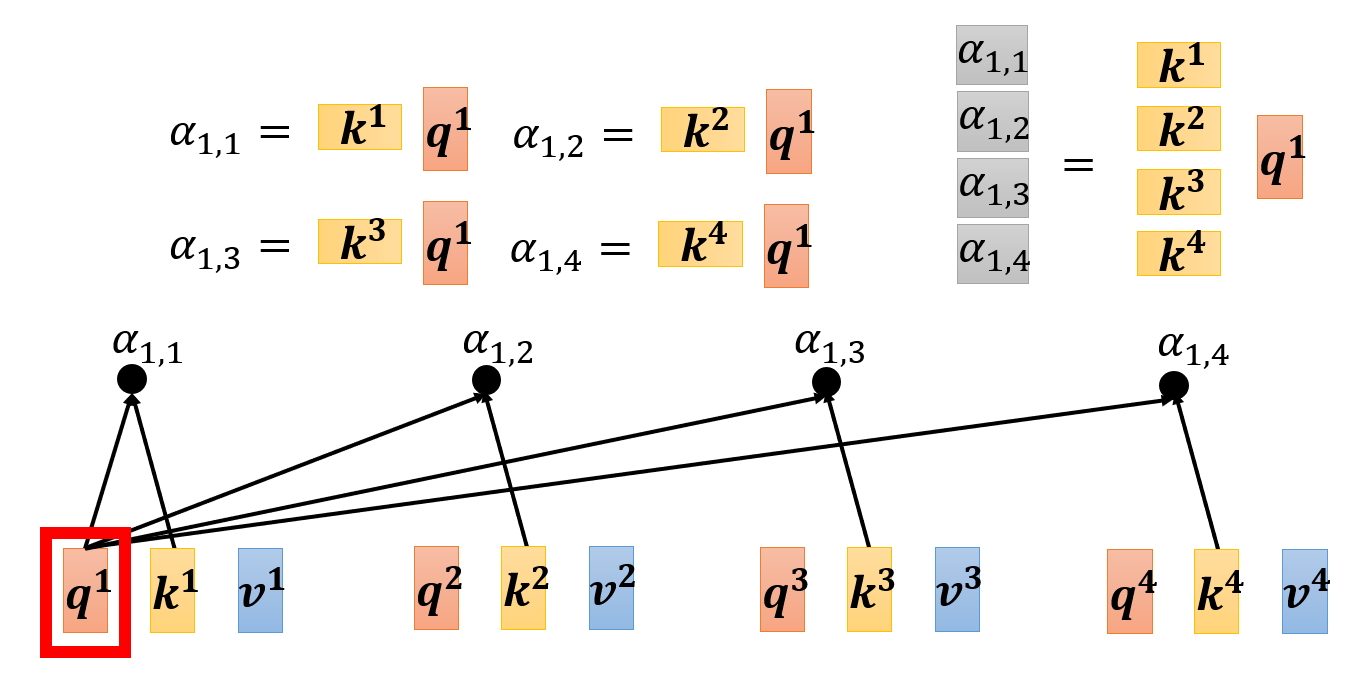
回到前面有 4 个输入的例子,先将 \(\bm{a^1}\) 作为查询,其他几个输入向量(也可以包括 \(\bm{a^1}\))作为键,计算相关程度 \(\alpha_{1, j}\ (j = 1, \dots, 4)\):
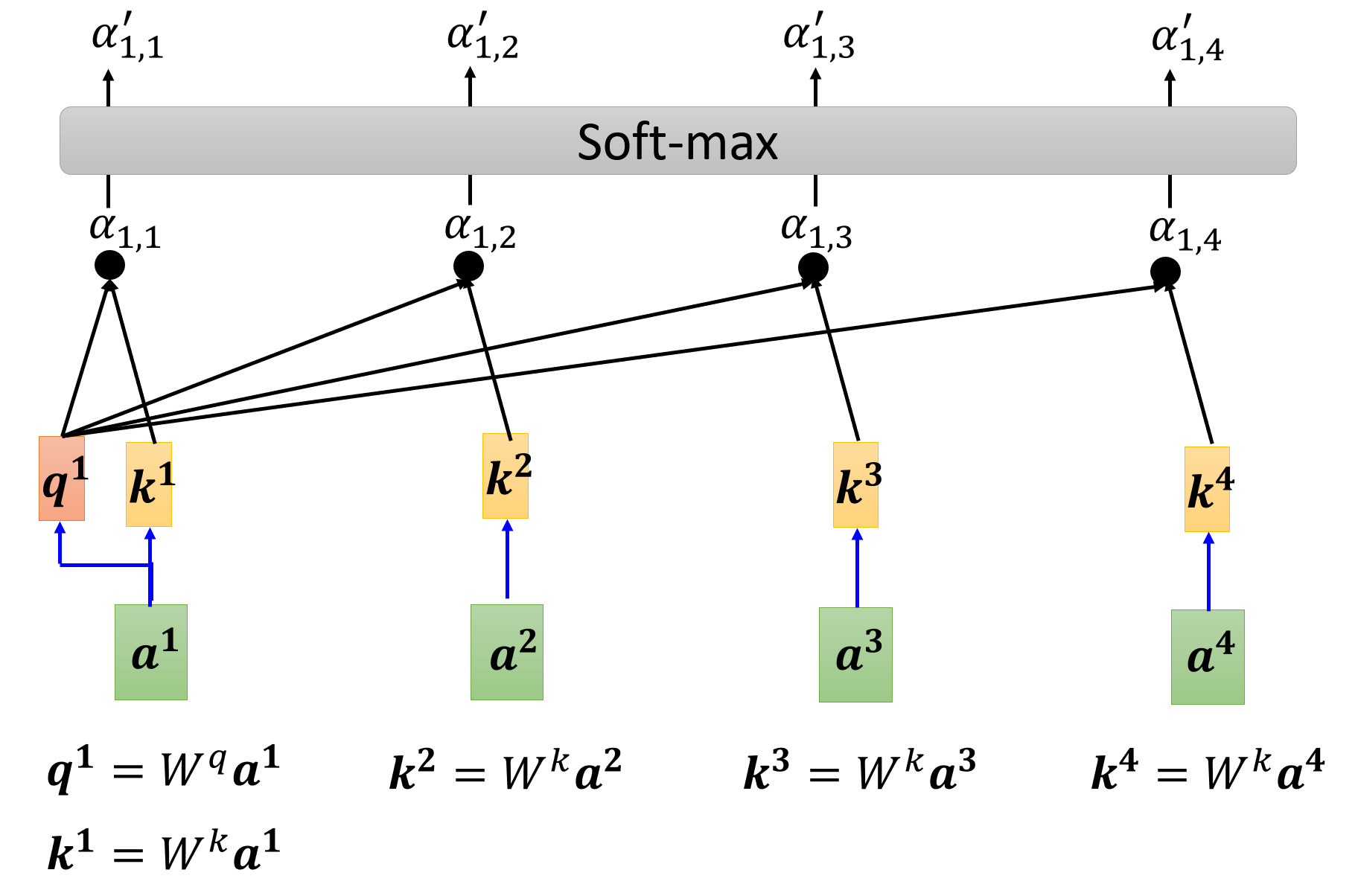
实际上,相关程度的值应该在 \([0, 1]\) 这一范围内,所以让这些相关程度值再经过一次 softmax 函数的运算,将它们的值映射到 \([0, 1]\) 上(用其他激活函数也没有问题
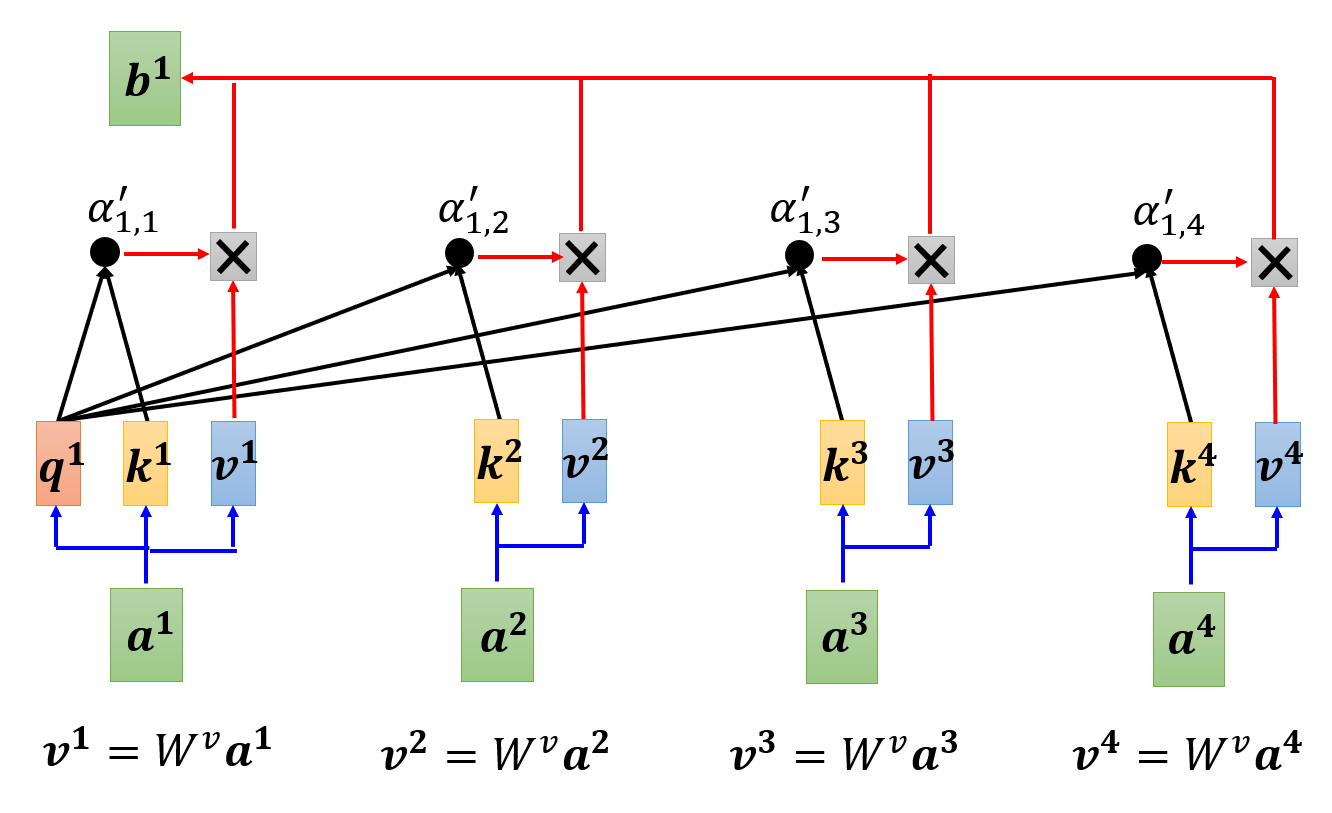
另外,对于每个输入向量,我们还要为它们计算第三个向量 \(\bm{v} = W^v \bm{a}\),然后将这个向量与刚刚经过 softmax 得到的相关程度值相乘,再将这些乘积相加(加权和
剩下的 \(\bm{b^2}, \bm{b^3}, \dots\) 等输出向量可以一起计算计算(并行计算
现在我们从矩阵的角度研究一般情况下的计算过程:
-
对于每个输入向量 \(\bm{a^i}\),需要得到三个向量 \(\bm{q^i}, \bm{k^i}, \bm{v^i}\),而这些向量分别通过三个矩阵 \(W^q, W^k, W^v\) 和 \(\bm{a^i}\) 相乘得到。与其让矩阵分别和单个的输入向量相乘,不如将这些向量拼在一起,形成一个矩阵,这样就将多次的矩阵 \(\times\) 向量的运算转化为一次的矩阵 \(\times\) 矩阵的运算,如下所示:
-
我们知道,计算相关程度 \(\alpha\) 的过程是一个向量乘法,但是我们也可以将其转化为一个矩阵乘法,一次性算出所有的相关程度值
-
先将所有的 \(\bm{k}\) 拼在一起,一次性计算某个查询下的所有相关程度:
-
然后将所有的 \(\bm{q}\) 拼在一起,这样就可以将所有的相关程度一次性算出来了!
-
-
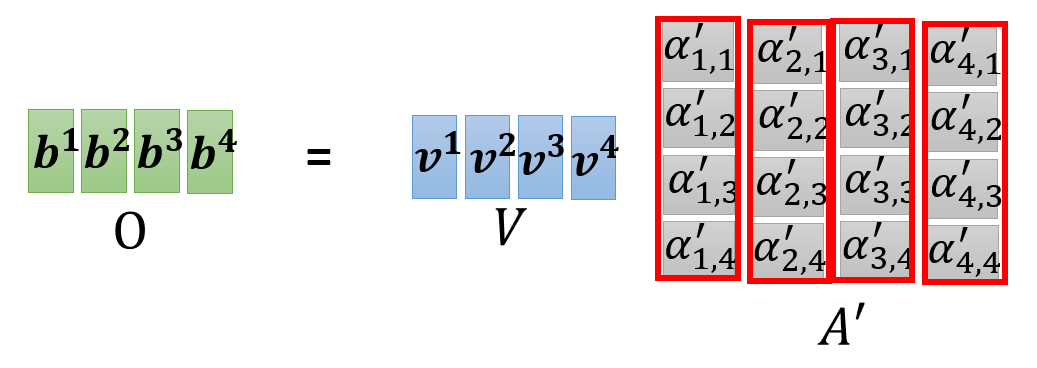
同理,将所有的向量 \(\bm{v}\) 拼在一起,与相关程度构成的矩阵 \(A'\) 相乘,得到所有的输出向量:
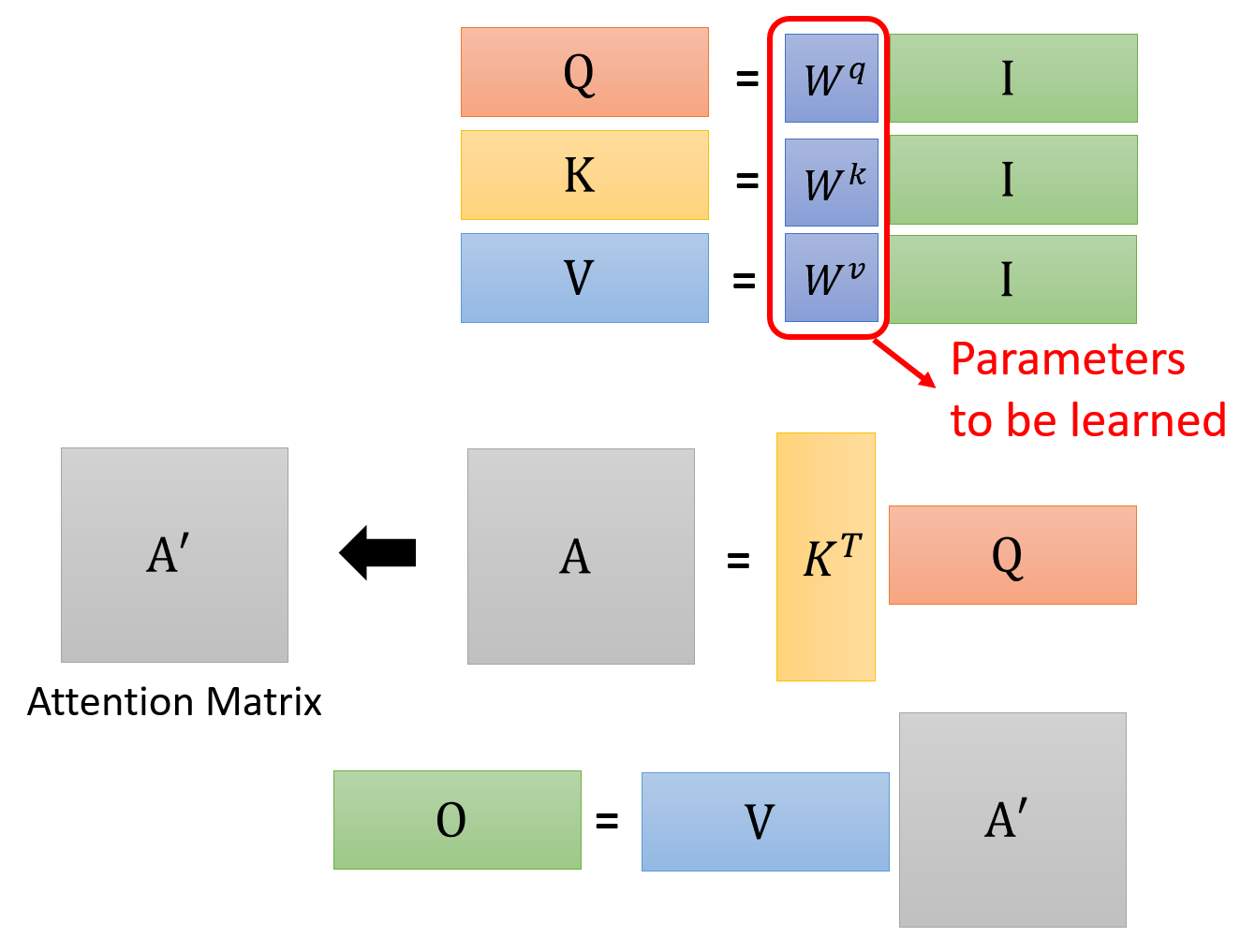
综上,整个自注意的计算过程可以抽象为以下一系列的矩阵运算:
其中三个矩阵 \(W^q, W^k, W^v\) 是我们需要通过训练学习的参数。而由相关程度构成的(且经过 softmax 归一化处理后的)矩阵称作注意矩阵(attention matrix)。
Multi-head Self-Attention⚓︎
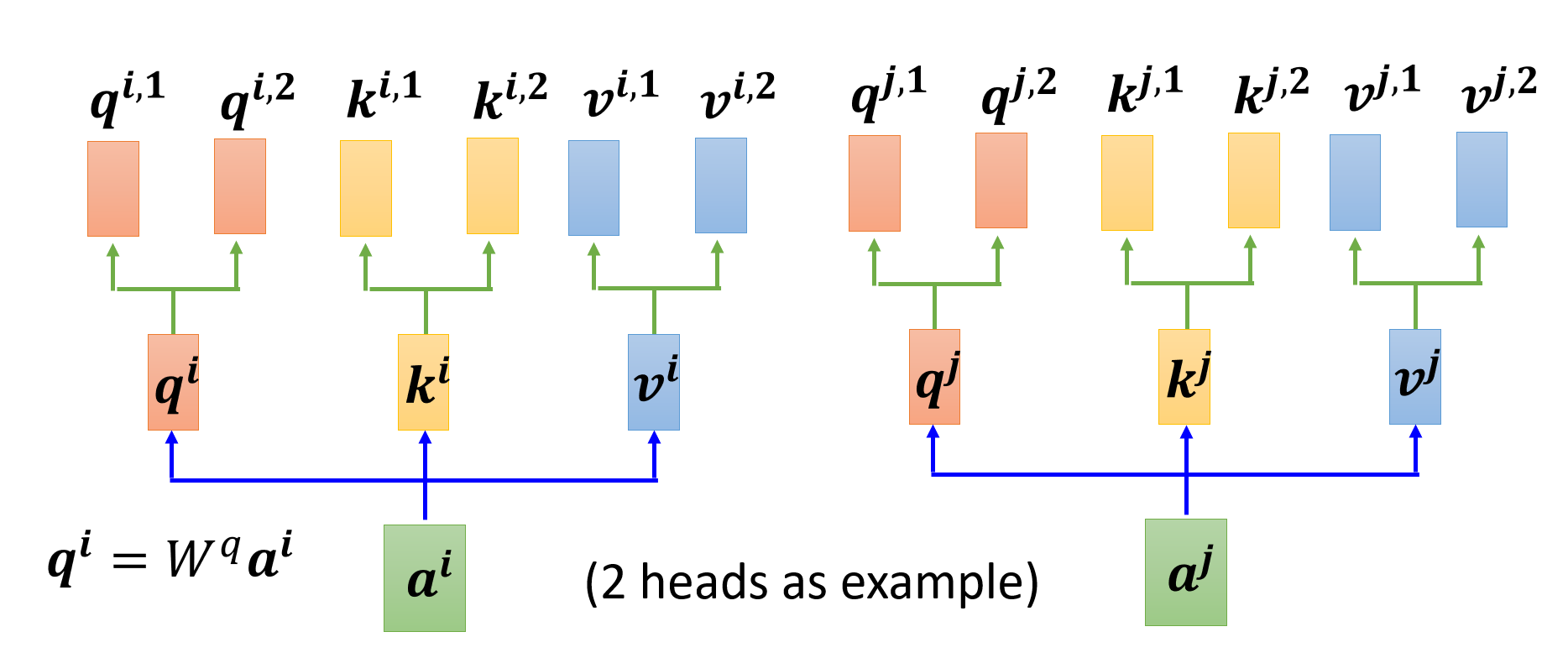
对于那些需要学习的参数 \(\bm{q}, \bm{k}, \bm{v}\),我们可以将同一个参数拆成多份(即“多个头”(multi-head),通过原参数 x 不同的矩阵得到
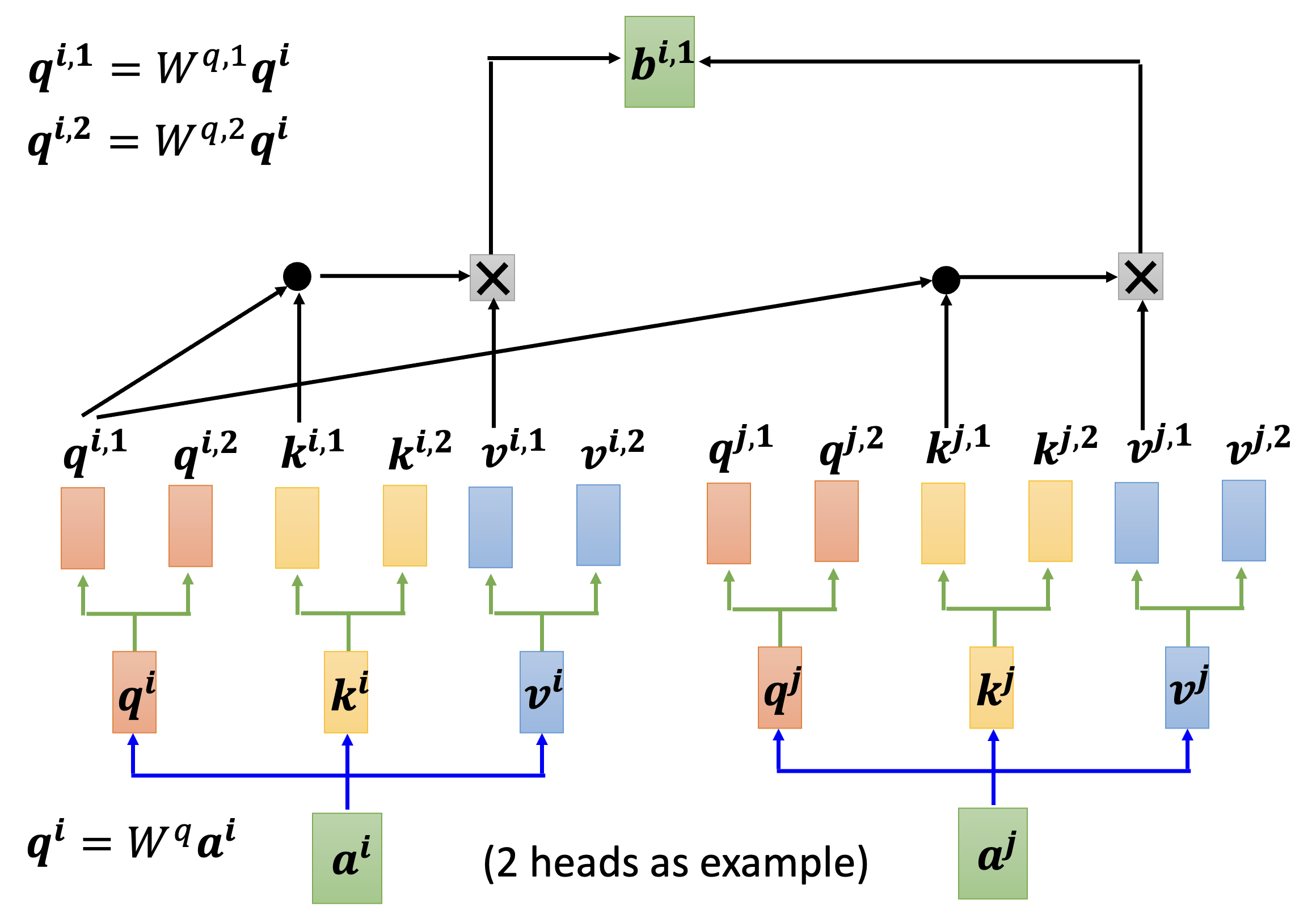
下面以第 \(i\) 个输入 \(\bm{a^i}\) 为例介绍输出 \(\bm{b^i}\) 的计算过程。先算出第一个头对应的输出 \(\bm{b^{i, 1}}\):
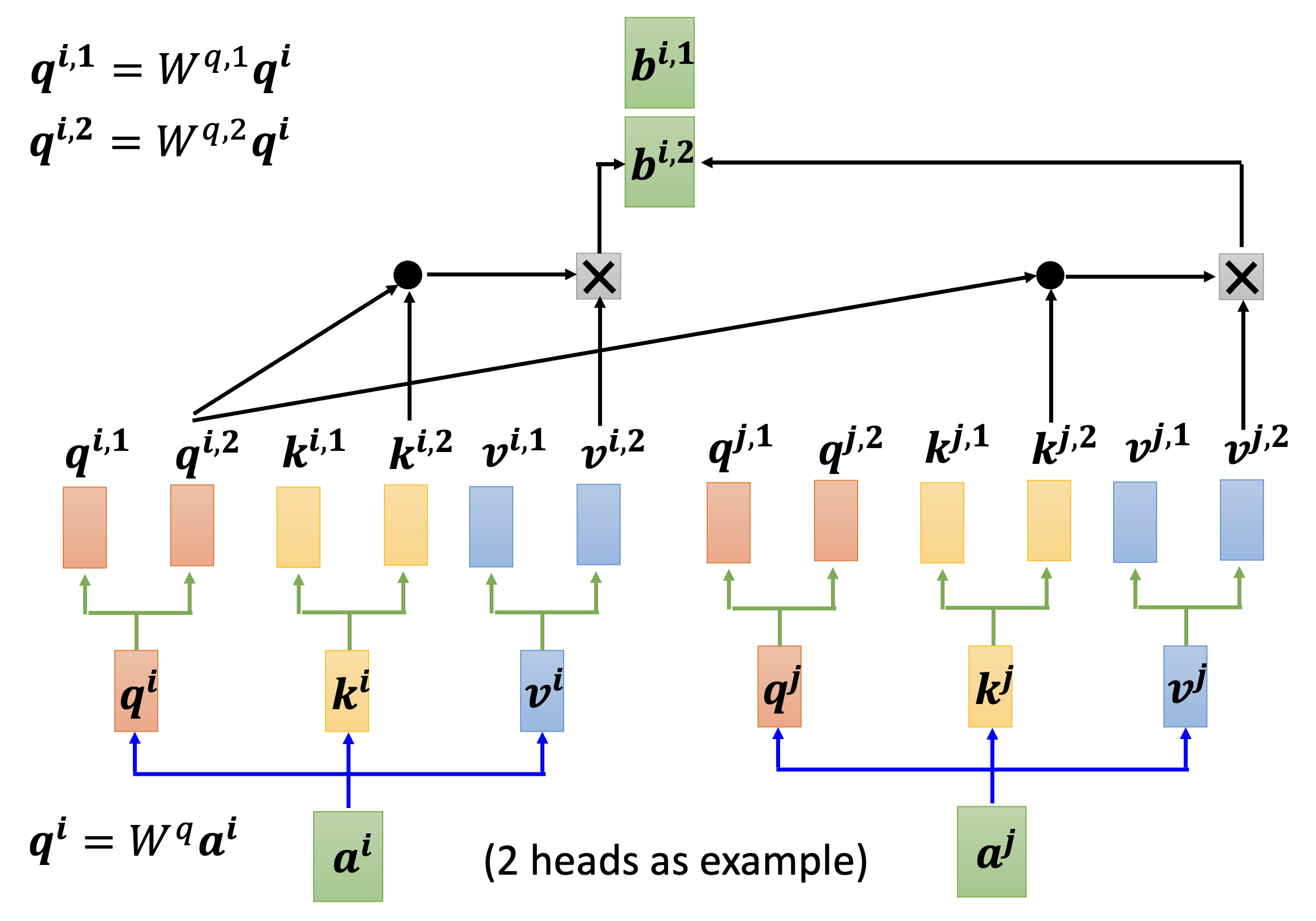
然后算出第二个头对应的输出 \(\bm{b^{i, 2}}\):
最后将这 2 个向量拼起来,乘上某个矩阵 \(W^O\) 后,就能得到完整的输出 \(\bm{b^i}\) 了:
Positional Encoding⚓︎
自注意机制的一个缺陷是:没有考虑位置信息,比如输入序列中第 i 个和第 j 个向量无论它们之间距离多远,都不会影响到它们在自注意机制中的计算结果。但有时候我们希望将这些位置信息考虑在内,比如在做词性标记的时候,我们知道动词一般不会出现在句首,这就是个值得考虑的位置信息。所以这里引入了一种叫做位置编码(positional encoding) 的技术——它会为每个输入向量设置一个唯一的位置向量 \(\bm{e^i}\),在进入自注意计算前,将其和输入向量 \(\bm{a^i}\) 相加,这样自注意计算时就将位置信息考虑进去了。
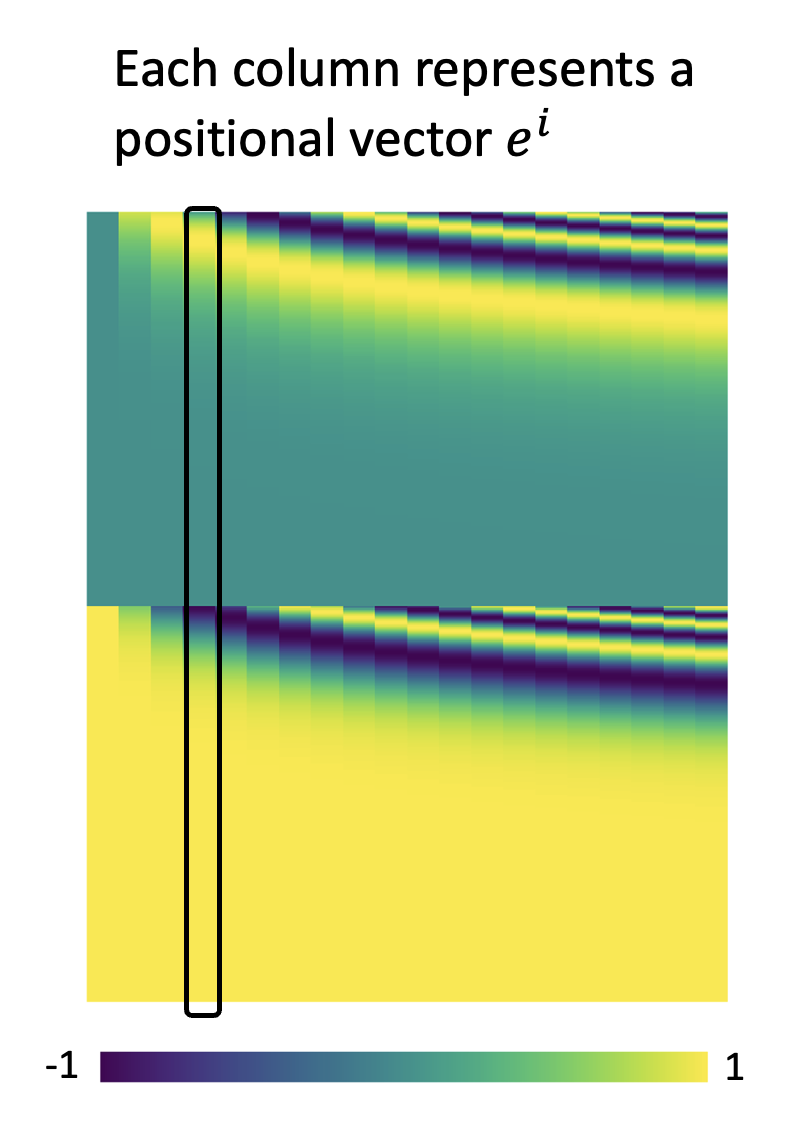
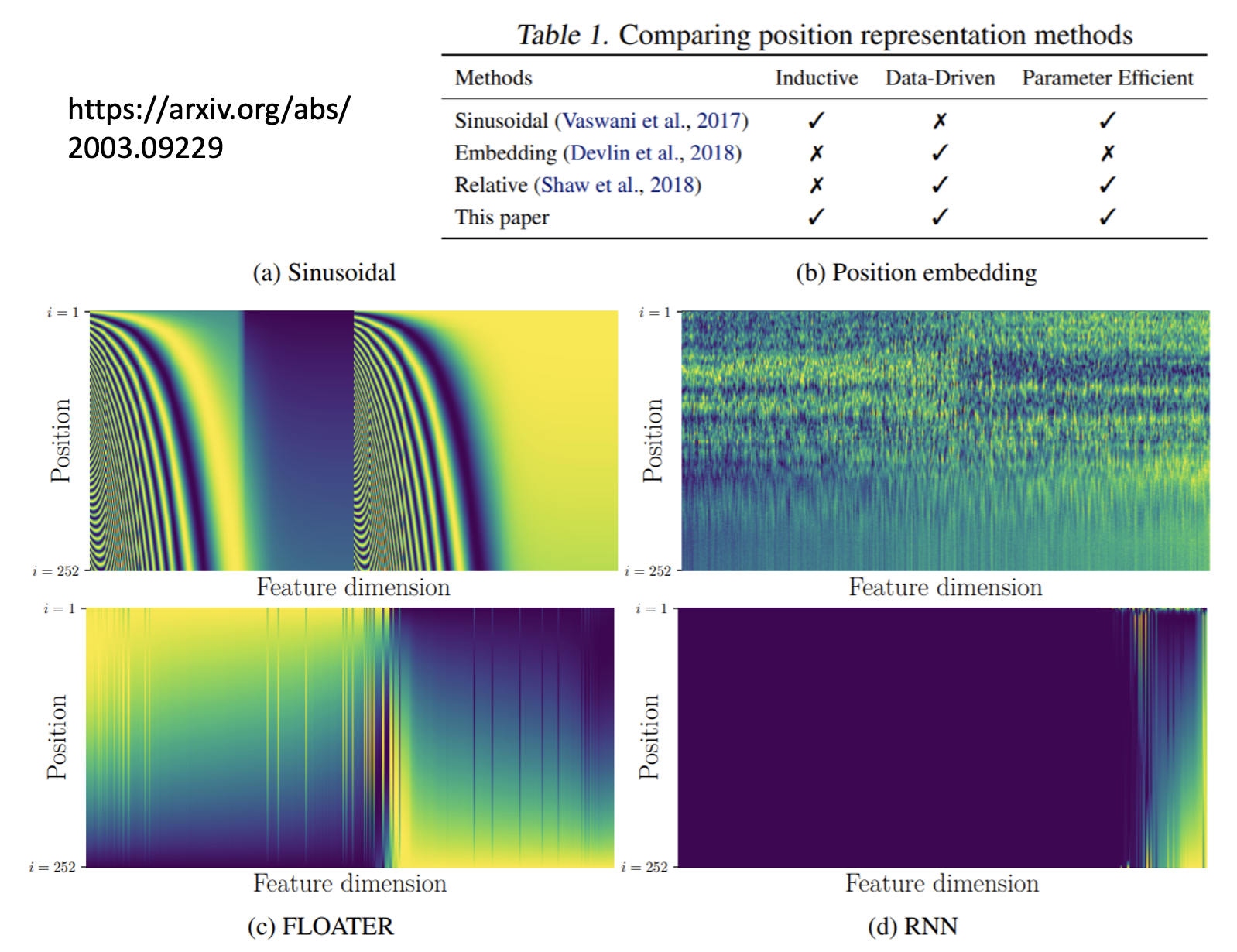
下图展示了一种可行的位置向量序列(这也正是经典论文 Attention Is All Your Need 中最早用到的位置向量
上面的位置向量是人为设定的(hand-crafted)——其实还可以通过数据训练出位置向量,下面就是一些典型的例子:
注意,这里的图需要横着看,也就是说一行表示一个位置向量。
Applications⚓︎
自注意机制被广泛应用在 NLP 中,而且我们熟知的 Transformer 和 BERT 中也用到了自注意。下面来认识一下常见的应用!
Speech⚓︎
在语音识别中也可以用自注意机制,但是存在一个问题:正如前面提到的,我们会把一段 10ms 的语音当做一个向量,那么随便将一两句话,这个输入序列的长度 \(L\) 就大到吓人;而且注意矩阵 \(A'\) 的规模是 \(L \times L\) 的,甚至大到无法被内存容纳。
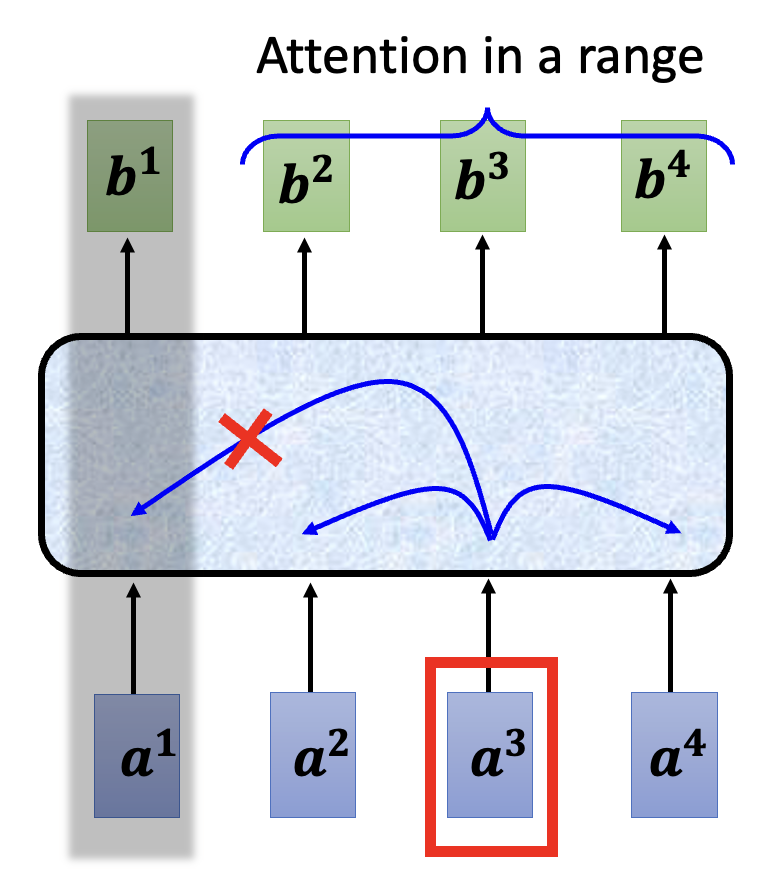
所以我们采取一种改进手段,叫做截断自注意(truncated self-attention)。简单来说就是:对于某个输入向量,我们仅考虑那些和当前输入向量比较接近的向量作为键,不去考虑更远的向量。在语音识别中,这种做法是合理的,因为要识别一句话中的一个字,我们往往无需得知整个段落的内容,也许仅靠这一句话甚至半句话就能判断出来了。
下面就是一个简化的示意图:
Images⚓︎
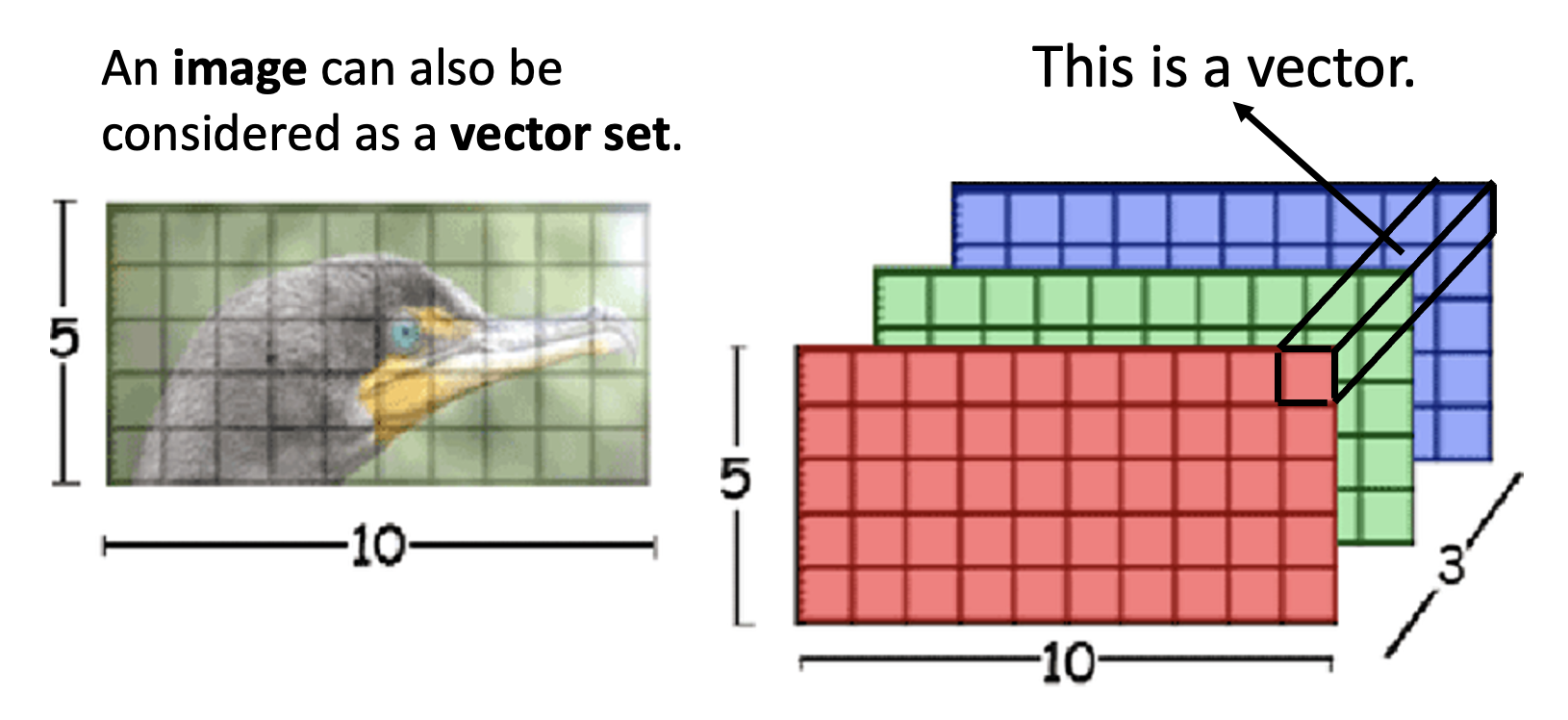
图像除了能用 CNN 来训练外,也可以用自注意来训练。我们可以将一张图像看作是一个向量集,而每个像素点就是一个向量,每个通道就是向量的元素。
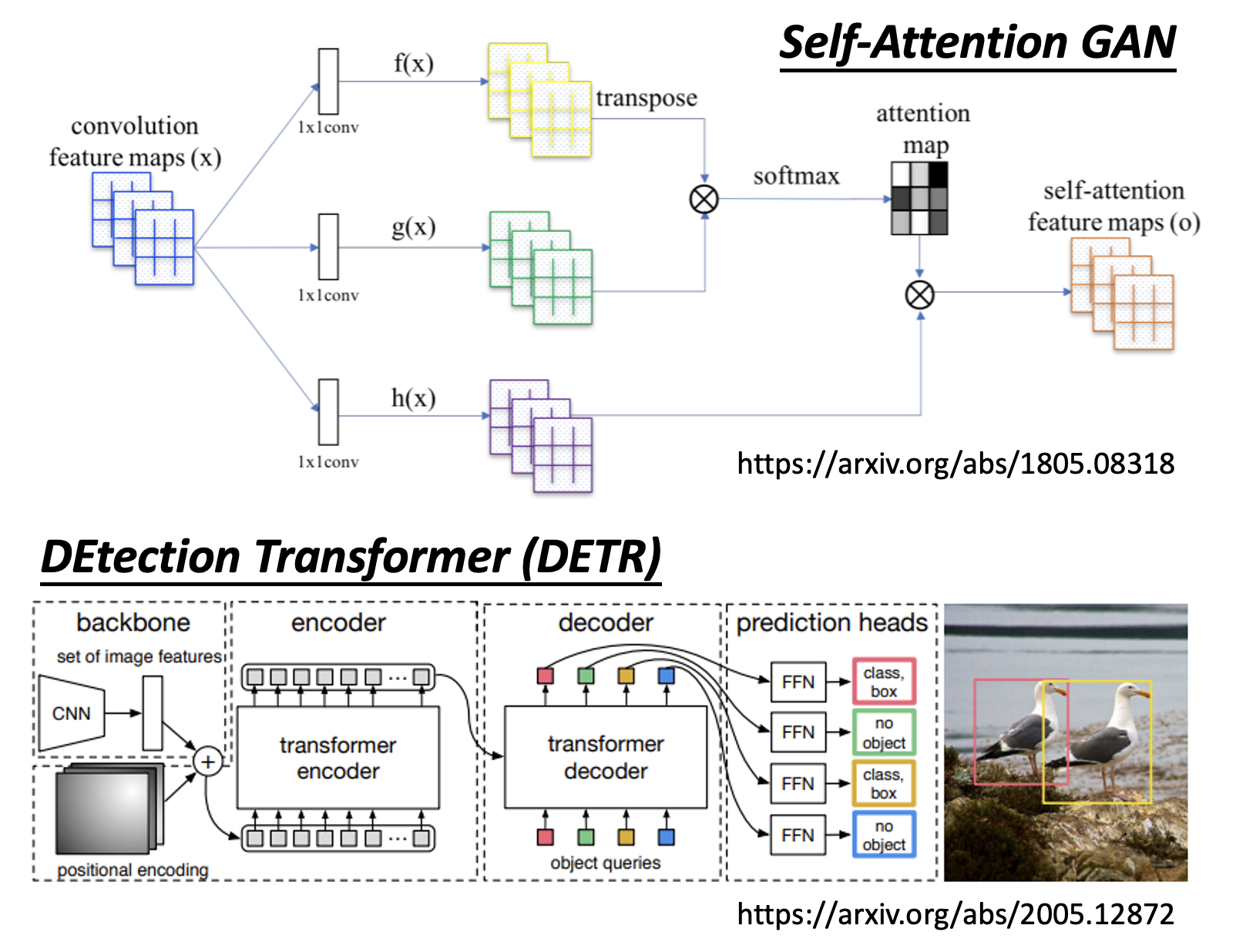
下面就是一些具体的应用:
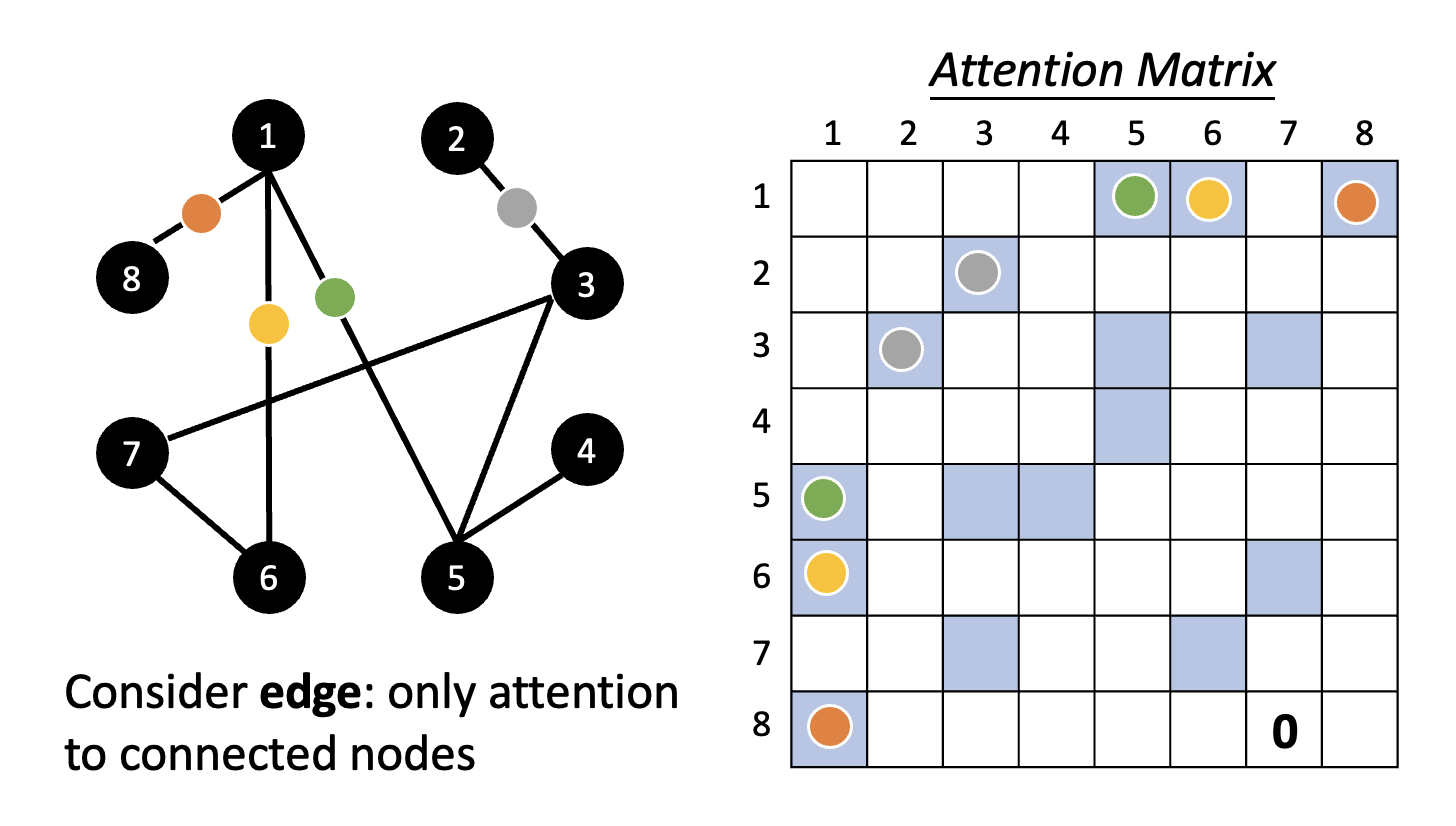
Graphs⚓︎
自注意 + 图 = 图神经网络(graph neural network)
这里利用了图的信息,尤其是边的信息。我们仅考虑有边相连的两个节点对应的注意矩阵上的元素(蓝色方框
Comparison⚓︎
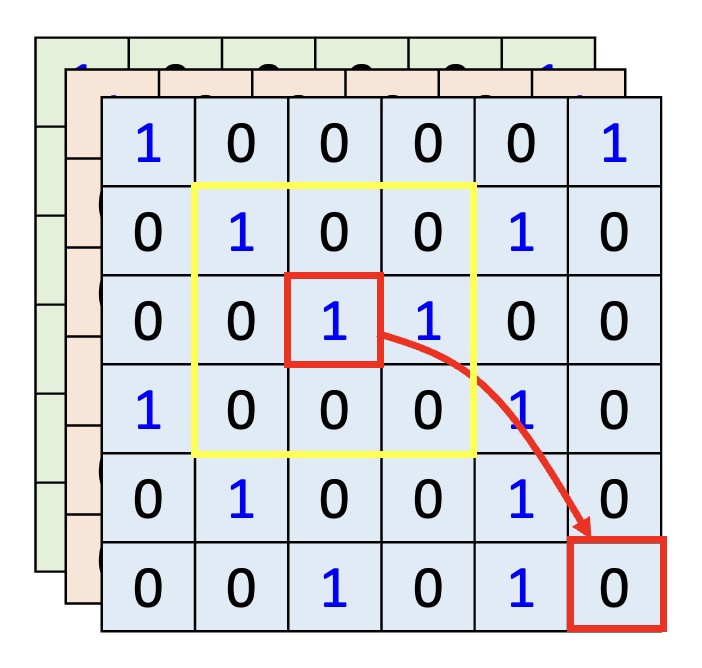
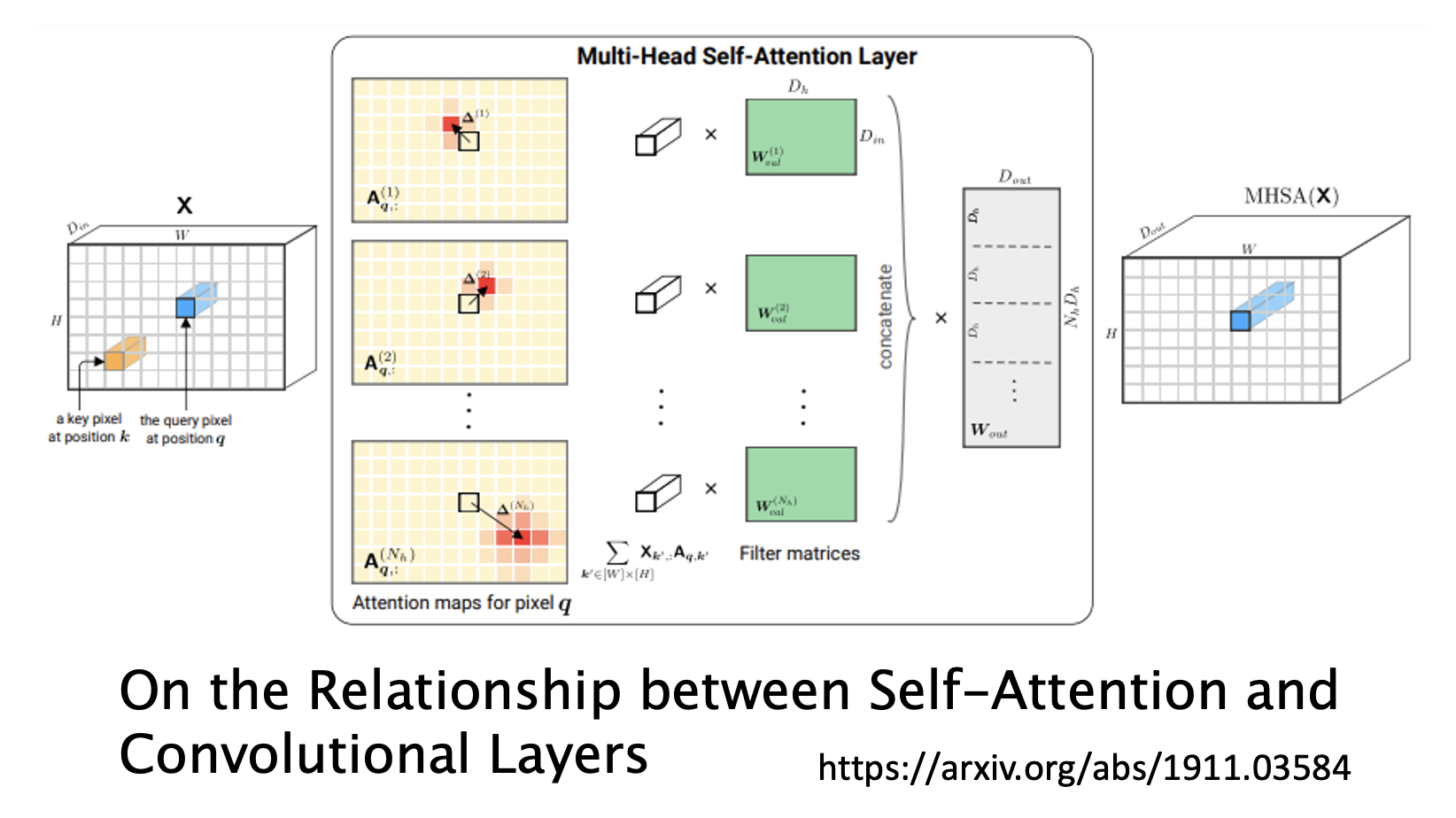
Self-Attention v.s. CNN⚓︎
上图中,黄色方框对应的是 CNN 的感受野,而红色方框对应的是自注意的查询和键。我们不难发现:
- CNN 是一种只考虑感受野范围内的自注意机制,即 CNN 是一种简化的自注意机制。
- 自注意机制是一种感受野范围更大(按 PPT 说法是可学习的 (leanable))的 CNN,即自注意机制是一种复杂版本的 CNN。
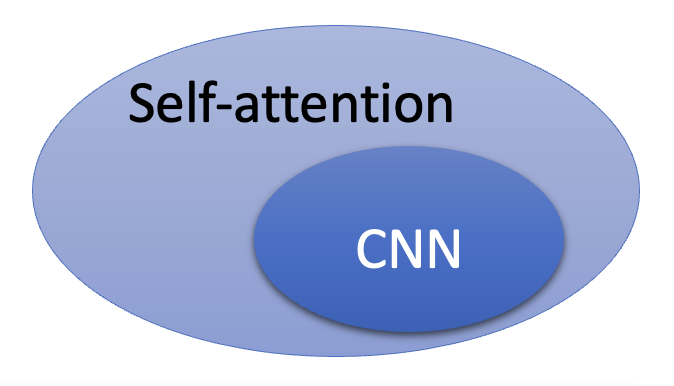
用维恩图可以形象表示两者的关系:
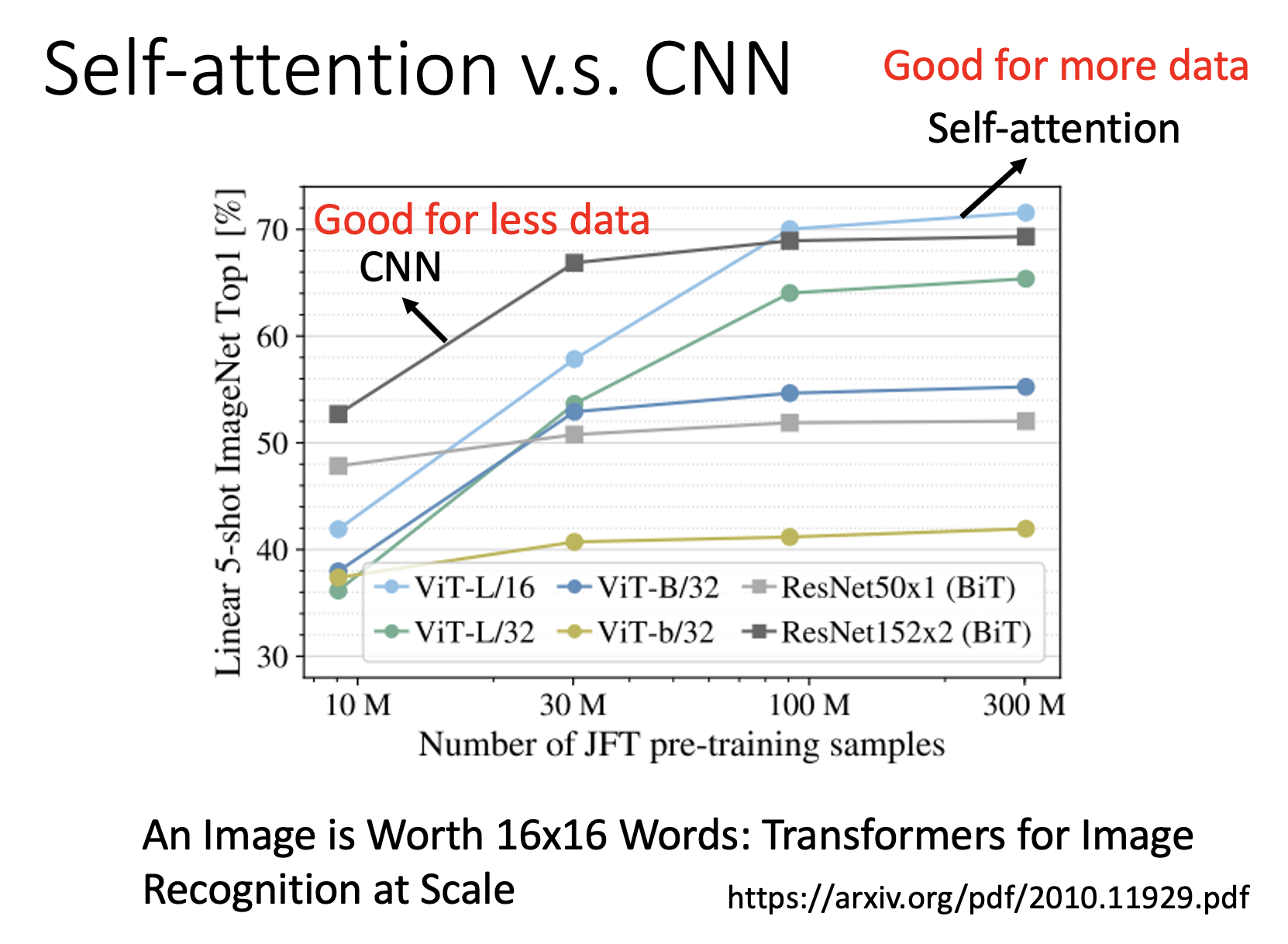
由于自注意机制会考虑更多的输入,因而更加灵活,所以在数据不多的情况下更容易出现过拟合现象,效果就不如 CNN 了;而一旦数据量大到一定程度后,自注意机制的优势就显现出来了。
下面这篇论文详细介绍了两者的关系,感兴趣的同学可自行上网搜索:
Self-Attention v.s. RNN⚓︎
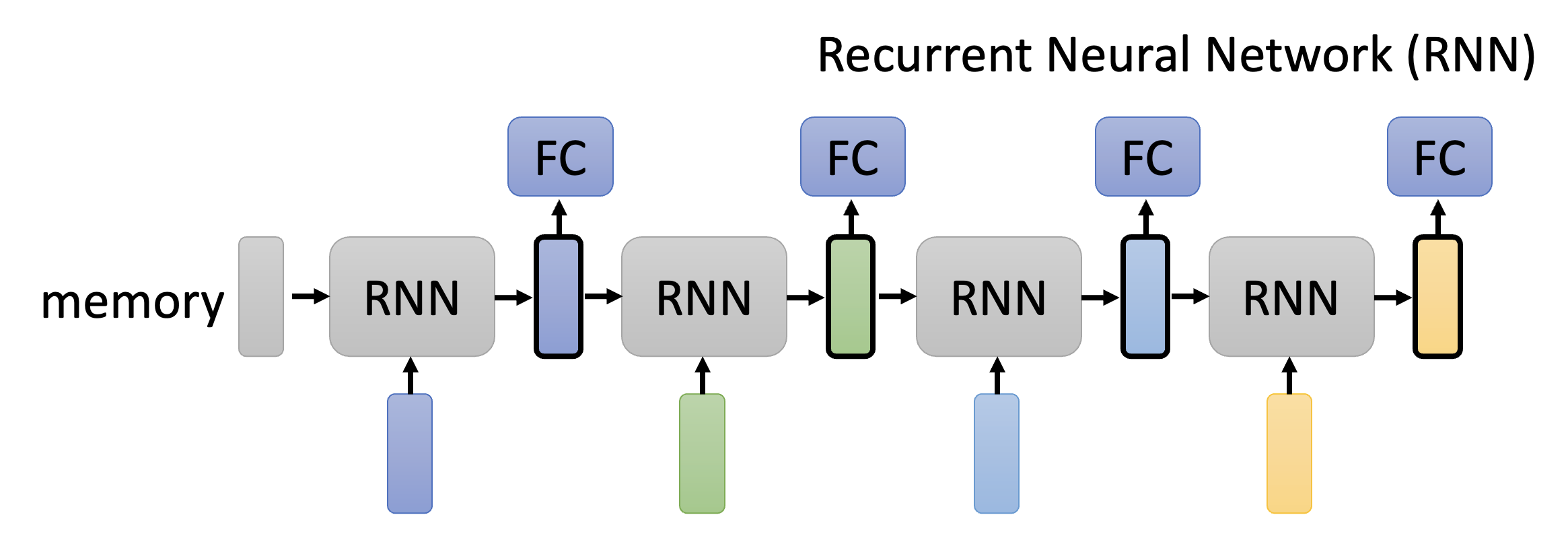
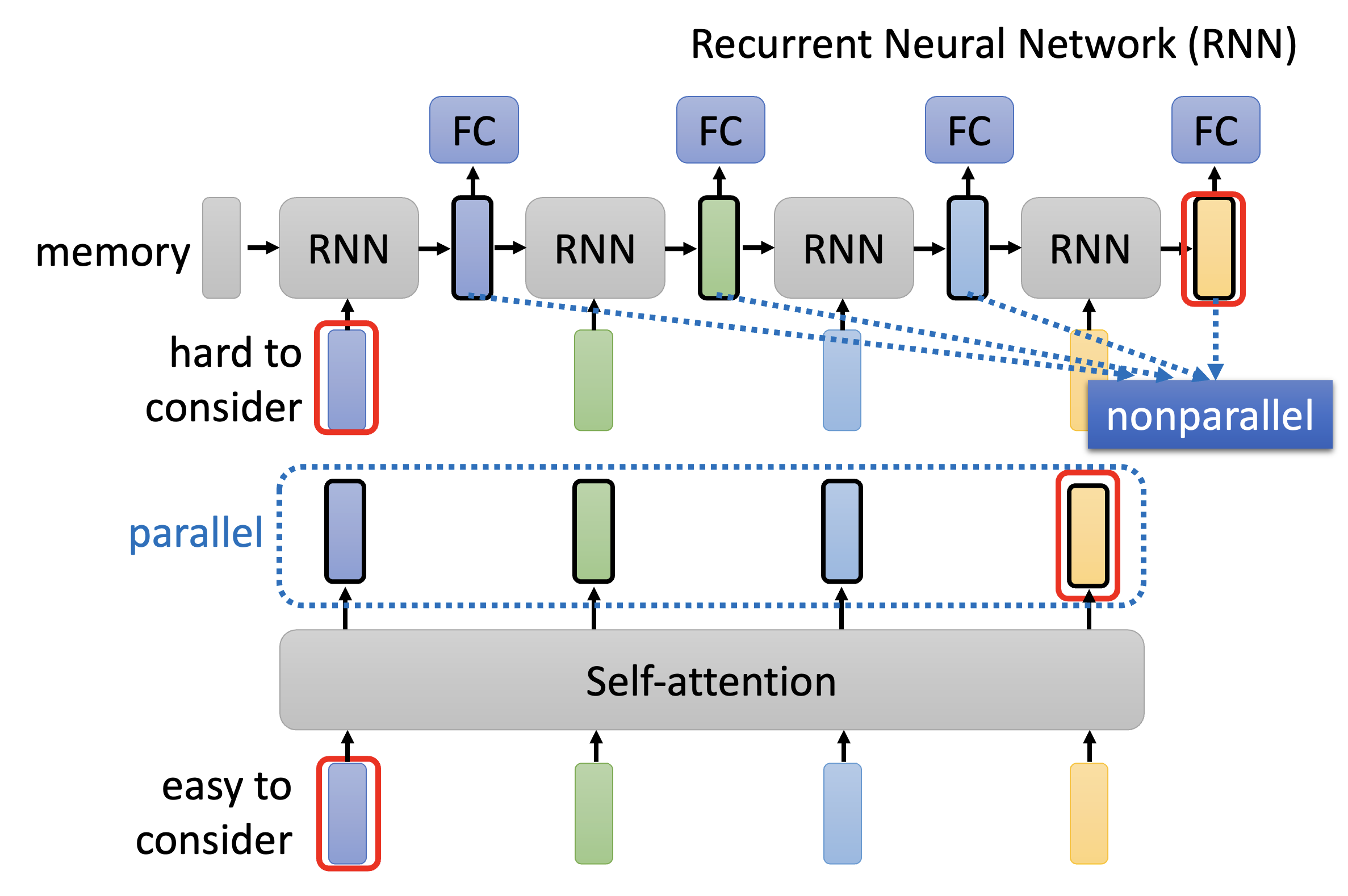
目前循环神经网络(recurrent neutral network, RNN) 基本上能被自注意机制给替代了,所以这里就简单介绍一下 RNN 的机制:
- 底下 4 个小矩形就是输入,最开始会有一个初始内存
- 将这块内存和第一个输入向量一同放到 RNN 中,得到一个输出(中间用黑框包裹的矩形
) ,该输出可进入 FC(全连接层)的训练中。 - 这个输出将和第二个输入向量一同放到 RNN 中,得到下一个输出,该输出也会进入 FC(全连接层)的训练中。之后就以此类推下去,故不再赘述。
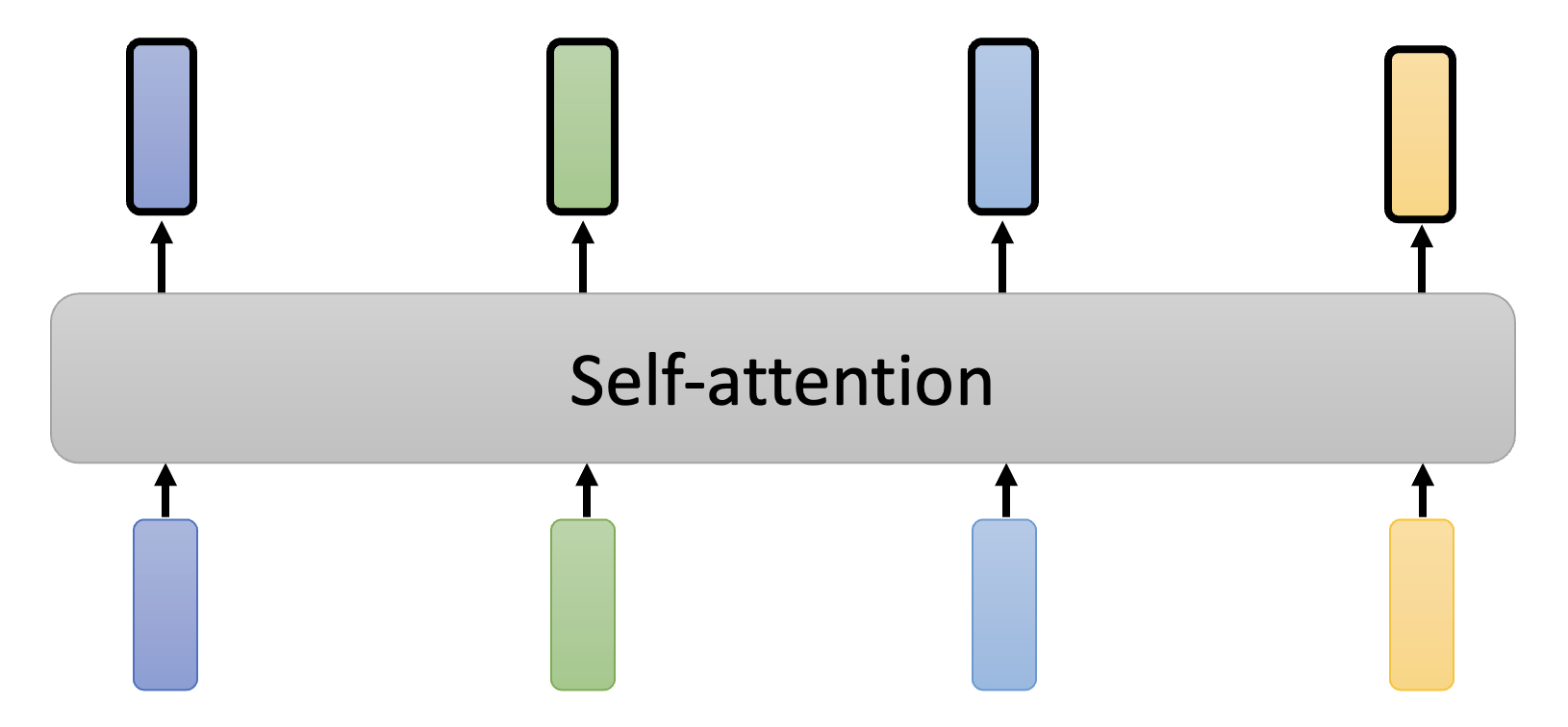
对应的自注意机制示意图为:
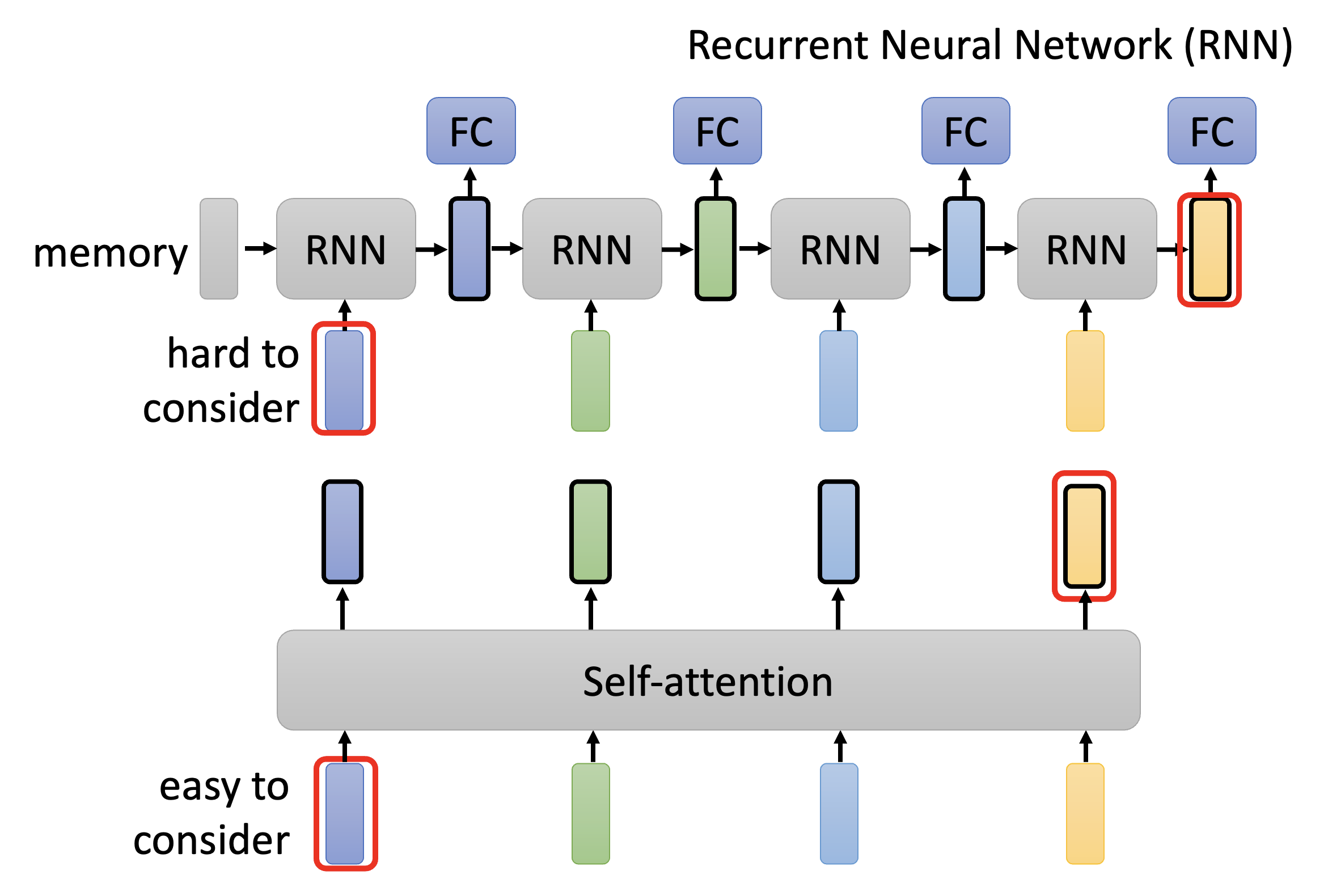
RNN 的劣势
-
难以考虑太远的输入向量:虽然我们可以将 RNN 改为双向的(这样的话输出向量都能包含任意输入向量,而不是像图示那样只能考虑左侧的输入向量
) ,但相比自注意机制能一次看透所有输入的能力,读取较远位置的输入向量还是有些差劲的。 -
无法并行:其实解释和前面的差不多,就是 RNN 需要一个个看输入,不能并行加速;而自注意能通过并行一次看完所有输入,所以效率之间有着很大差别。
正因为这些劣势,那些采用 RNN 的应用开始改用自注意机制了。
Variants⚓︎
前面介绍的都是一般的自注意机制技术,实际上后人们在此基础上设计出各种“魔改版本”,想要在确保不影响表现的同时提升效率。下面我们就来认识这些各式各样的自注意机制变体吧!
Skipping Some Calculations with Human Knowledge⚓︎
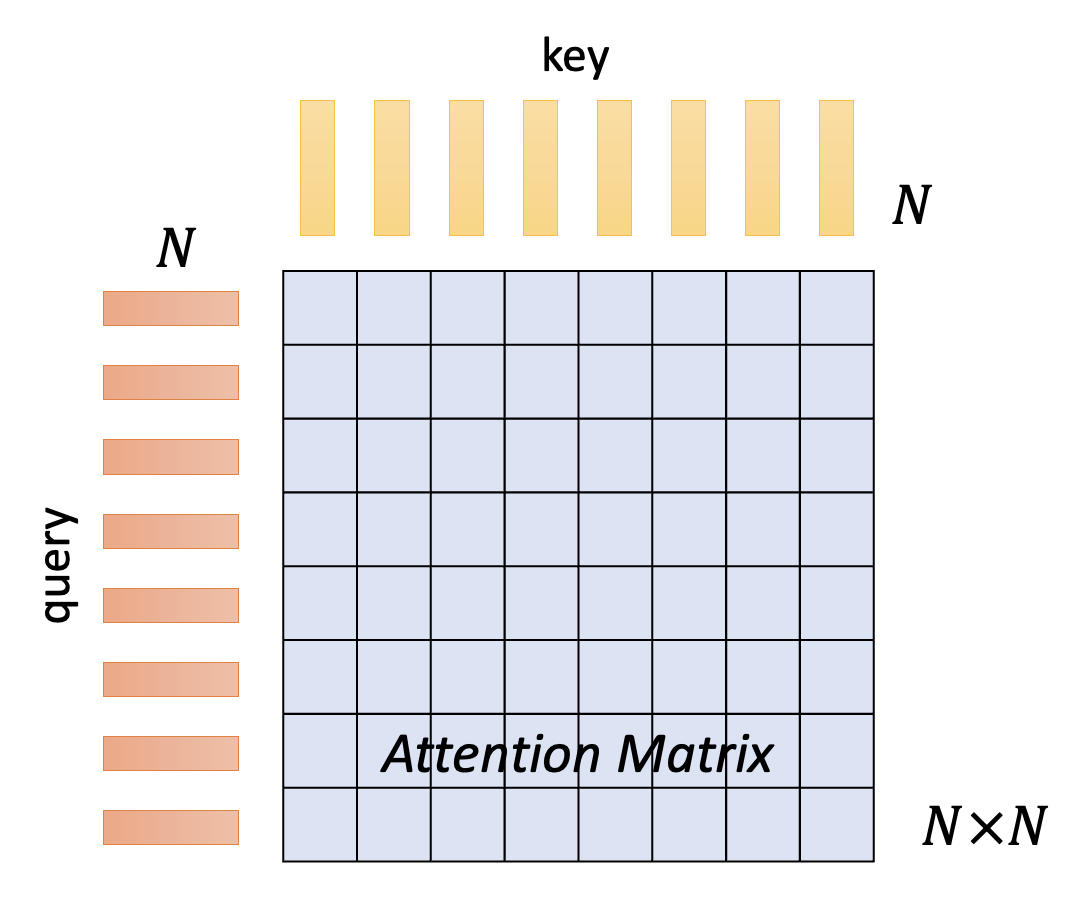
先来回顾一般的自注意机制:假如序列长度为 \(N\),那么中间产生的查询和键的数量也是 \(N\),而查询序列和键序列相乘得到的注意矩阵的规模就是 \(N \times N\) 的了。
另外,我们还有以下发现:
- 自注意机制只是整个网络中的一个模块
- 当 \(N\) 很大时,自注意机制决定了整个的计算量
- 上一点通常体现在图像处理等任务中
- 比如有一张 256x256 的图片,那么 \(N = 256 \times 256\),注意矩阵就有 \(256^4\) 个元素,足以体现计算量之大
第一种提升计算效率(或减小计算量)的思路是利用我们人类已有的知识来避免不必要的计算。下面给出一些具体的方法。
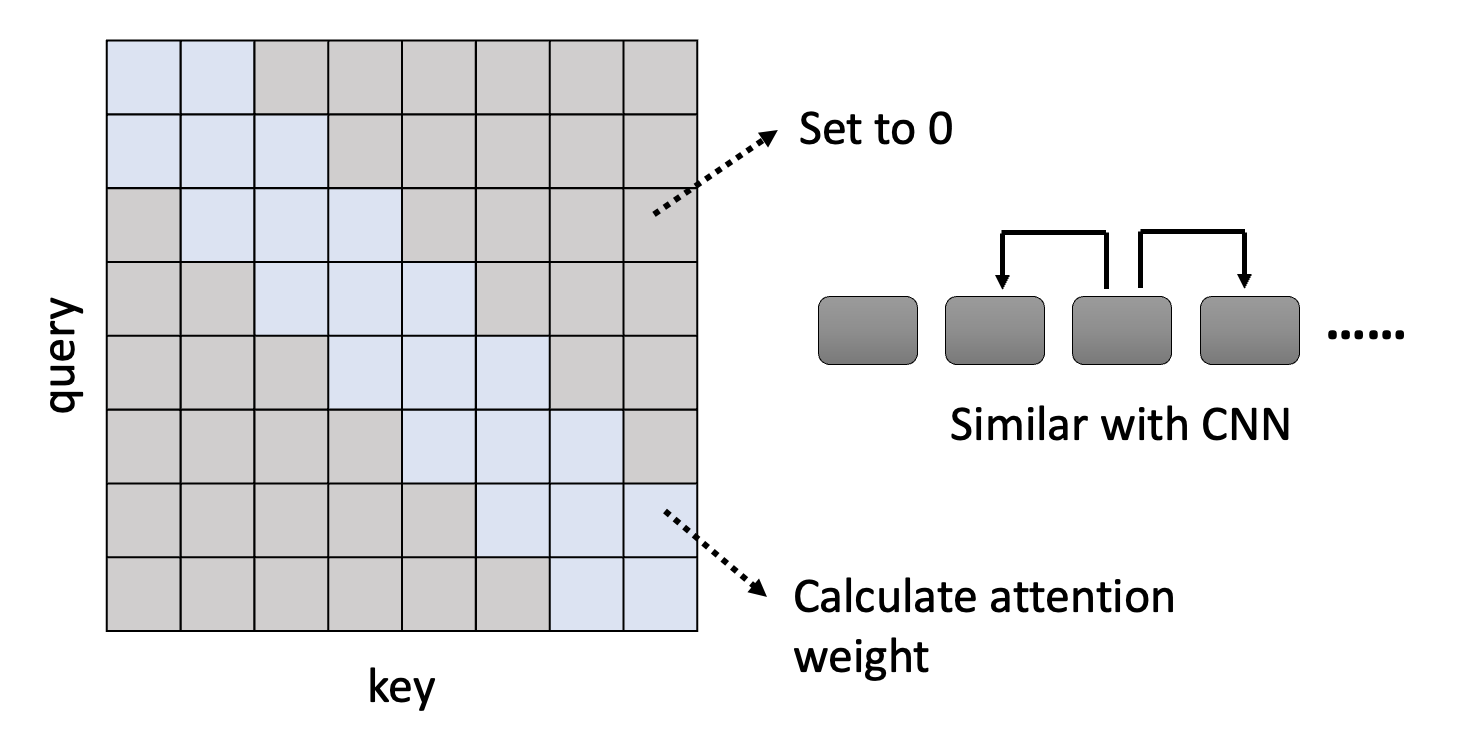
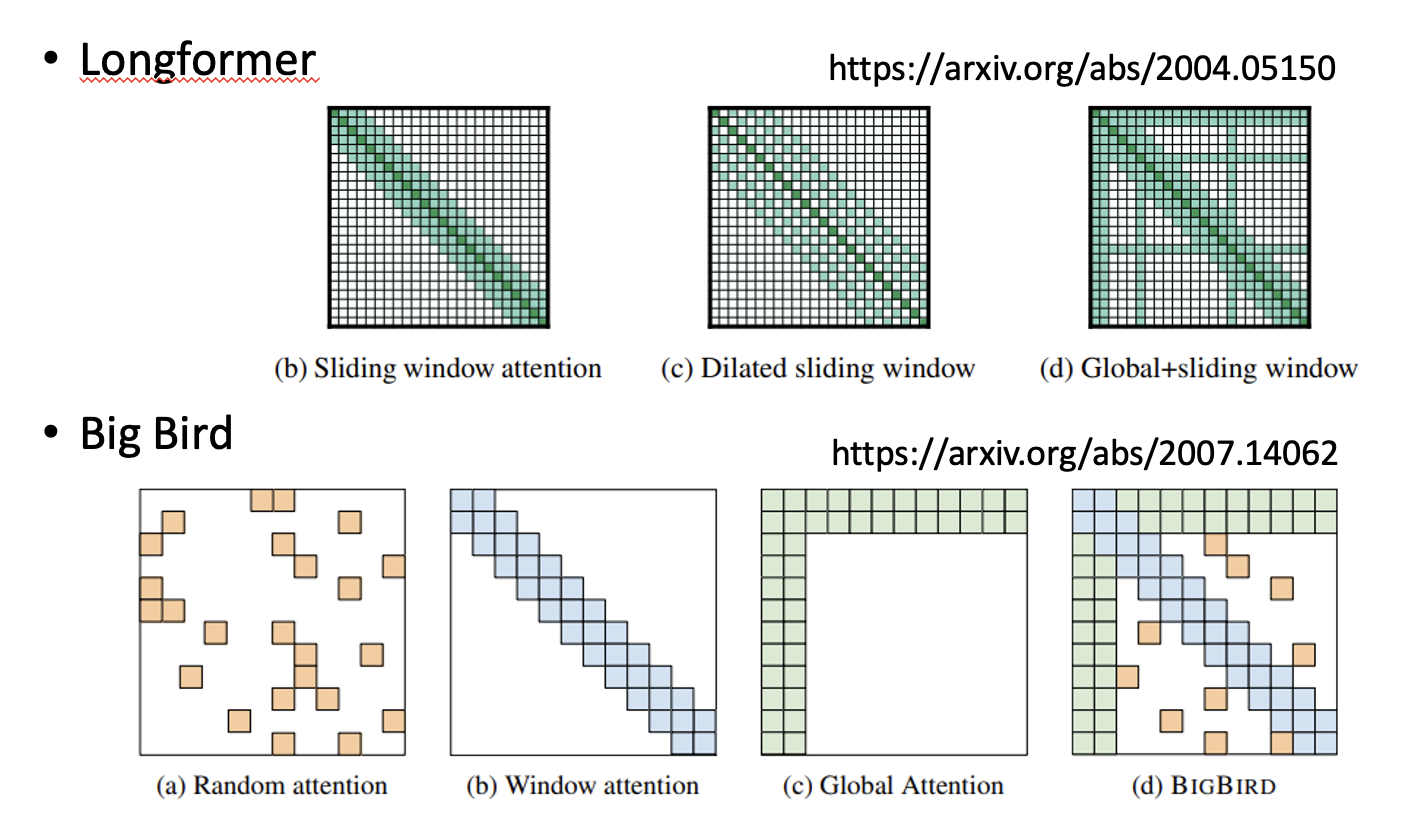
Local Attention/Truncated Attention⚓︎
- 注意矩阵中灰色方块对应的元素直接置 0,不去计算;蓝色方块对应的元素需要计算注意权重
- 该方法的思路是:输入向量只看相邻的 2 个向量,其他向量就不去管它
- 思路上和 CNN 类似
- 该方法能够加快计算速度,但不一定能给出非常好的结果
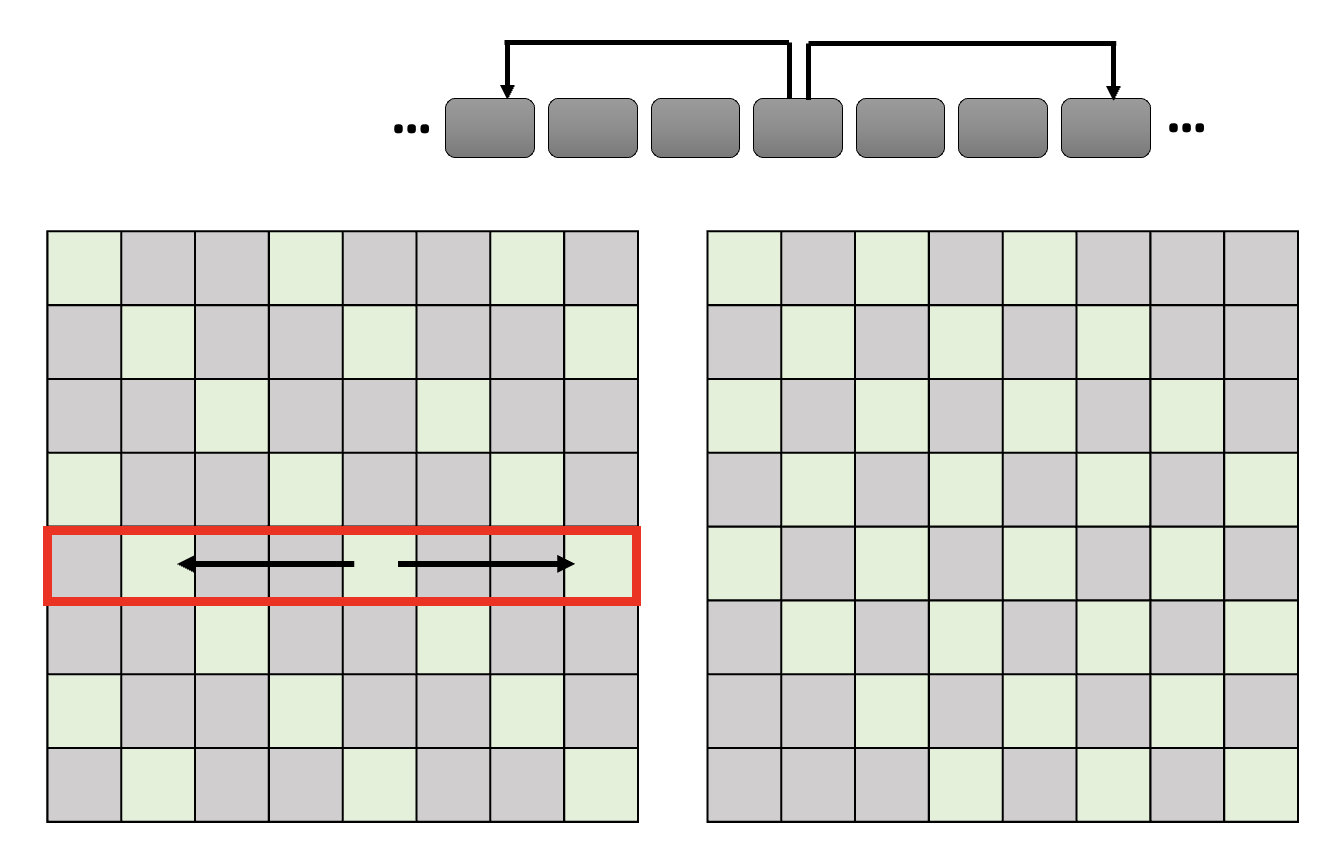
Stride Attention⚓︎
- 类似前一种方法,但是看的是跳过几个向量后的向量
- 跳过的步幅可以根据任务需求自行调整
Global Attention⚓︎
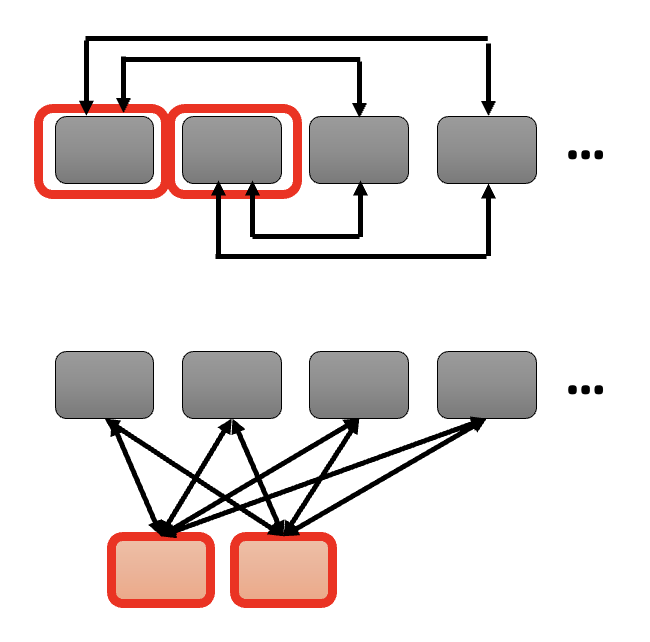
全局注意(global attention) 的思路是:
-
在序列中设置一类带有特殊记号的向量
-
可以给原向量做特殊标记(上图
) ,也可以插入带有这种特殊记号的新向量(下图)
-
-
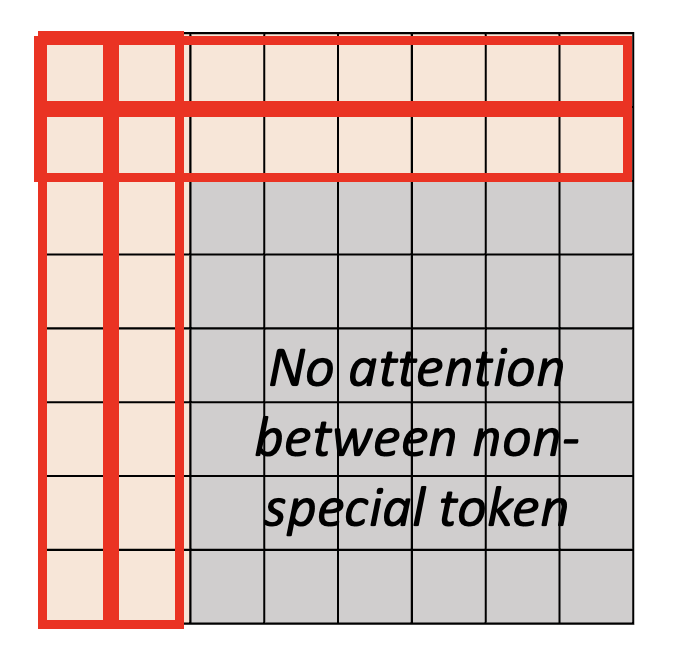
这些特殊向量会考虑序列中所有的向量,因而掌握了全局信息
- 其他向量也会考虑所有的特殊向量,从而得知全局信息
- 一般向量就不会考虑其他一般向量
上述这些方法并不互相排斥,实际上可以一起使用(小孩子才做选择,我全都要!
Focusing on Critical Parts⚓︎
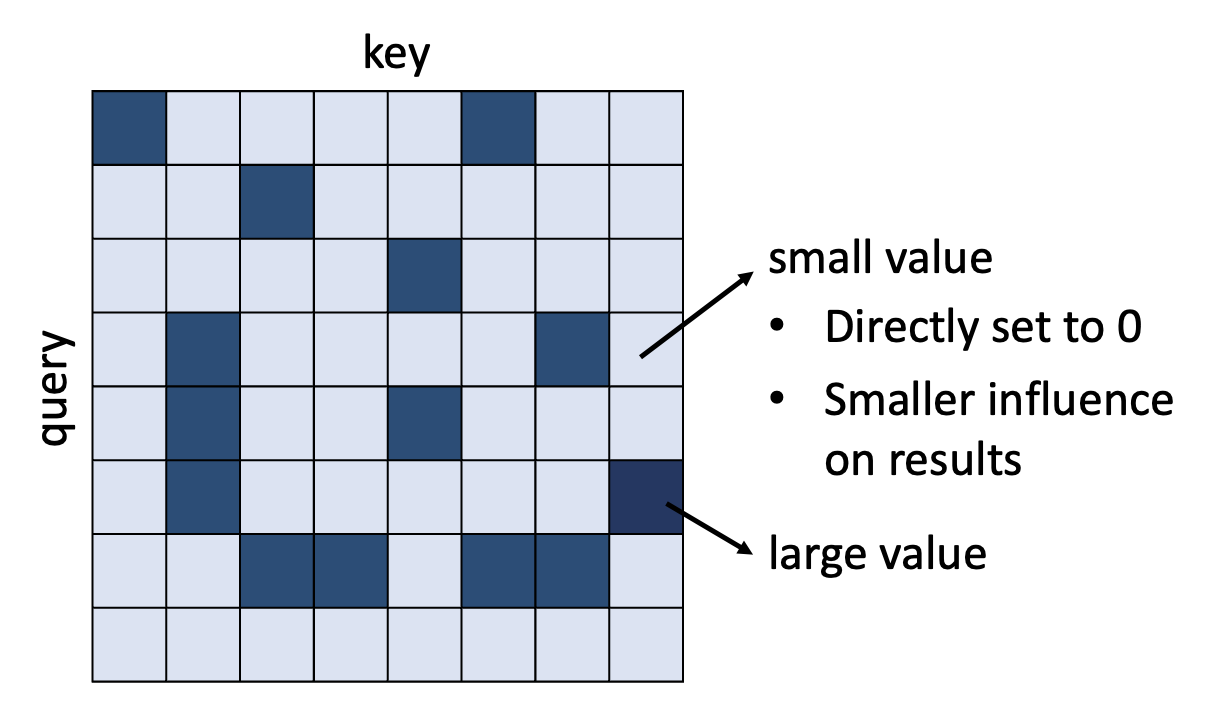
上面通过人类知识简化计算的思路不一定给出最好的结果,所以我们来看另一种思路:对于一个已有的注意矩阵,每个元素的值有大有小。我们决定:
- 对于较小的值,直接设为 0,因为它们的影响不大,可以忽略
- 所以计算时只关心较大的值
那么,接下来的问题就是:如何快速评估较小注意权重的占比呢?下面介绍一些相应的技术。
Clustering⚓︎
注
Reformer 和 Routing Transformer 用到了这类技术。
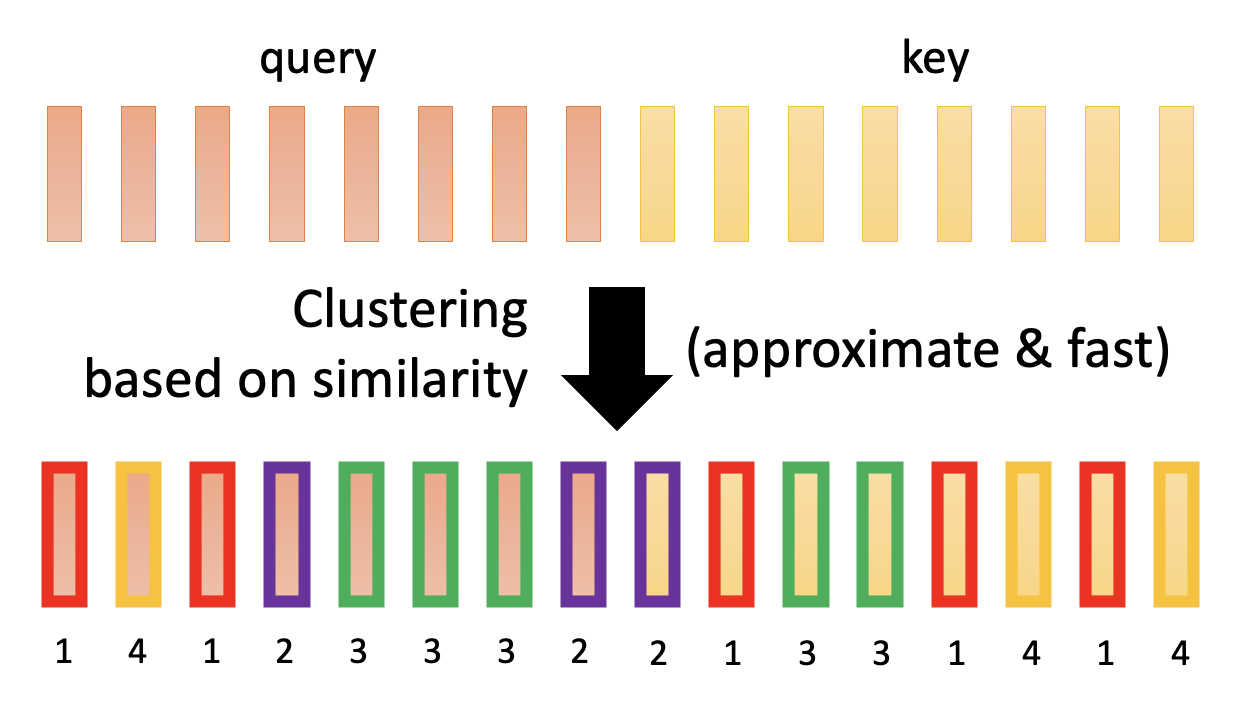
聚集(clustering) 技术的步骤如下:
-
基于查询和键的相似性分成多个集群 (cluster)
- 该步一般采用近似方法来做,计算量不会很大
- 下面的例子就是将查询和键划分成 4 个集群
-
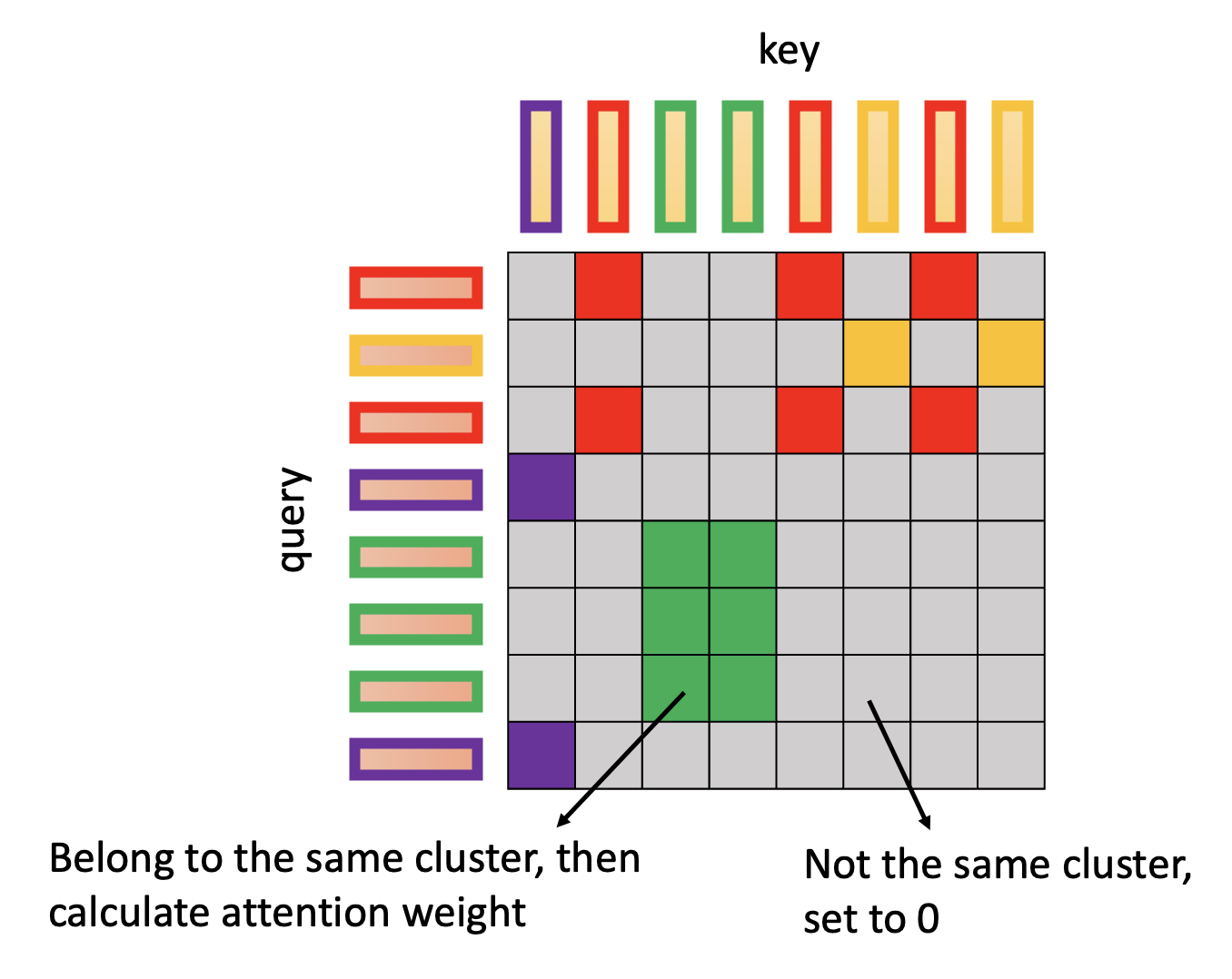
在注意矩阵中,我们只计算那些位于同一集群中的查询和键的乘积,不同集群的就不去计算,直接置 0 就好了
Learnable Patterns: Sinkhorn Sorting Network⚓︎
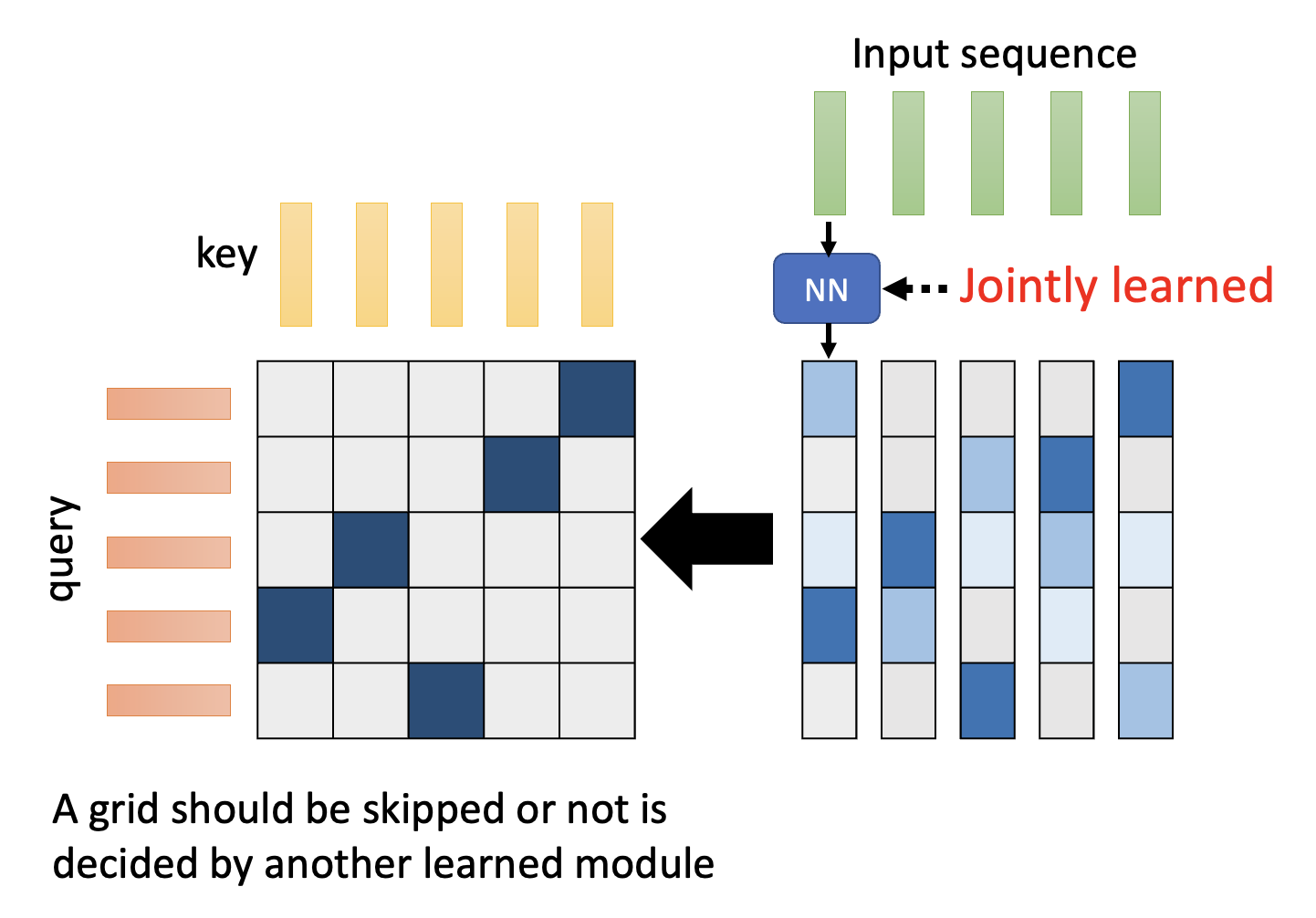
到目前为止,所有的技术都是基于人类知识来实现的,但实际上还可以通过机器学习,让模型自己决定哪些注意权重需要计算,哪些可以忽略。有一种叫做 Sinkhorn 排序网络(Sinkhorn sorting network) 的技术便能做到这一点。
大致思路如下:
- 输入序列的每个向量会经过一个神经网络,得到一组规模和注意矩阵一致的向量,这组向量会转化成要求的注意矩阵
- 然而注意矩阵的注意权重只有 0 和 1(离散的
) ,而刚刚得到的那组向量是连续的,因此需要做进一步的处理 - 这个处理过程正是原论文探讨的重点,这里不会细讲,感兴趣的读者可以网上搜索阅读
- 由于通过神经网络得到的向量组是可微分的,因此可以通过训练提高精度
- 实际上在原论文中,多个输入向量会共用一个经过神经网络得到的向量,从而减小计算量
- 但这样得到的向量组规模就比注意矩阵小了,因此在转化时还要“放大”这个向量组,使得规模匹配的上
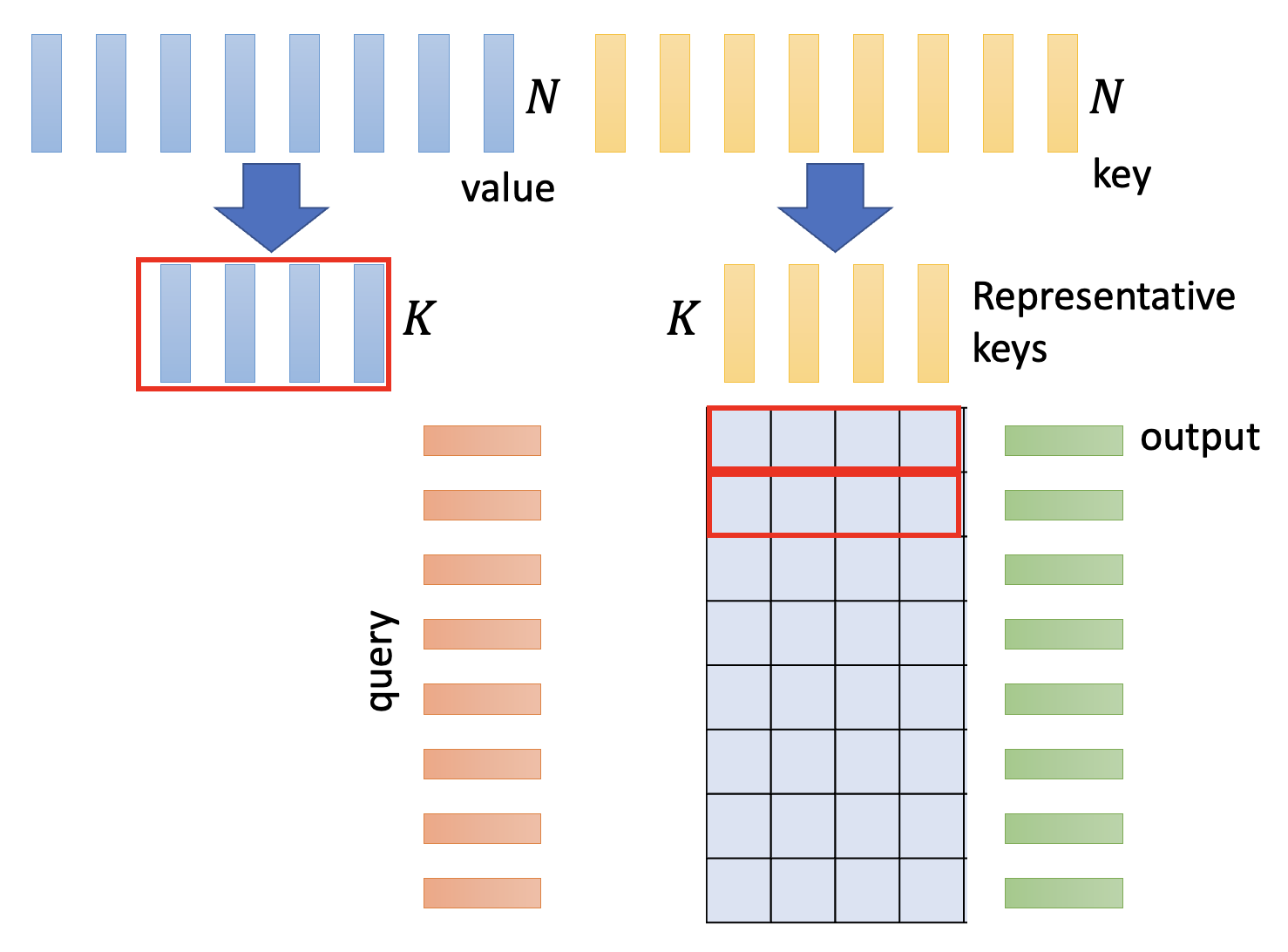
Reducing Number of Keys⚓︎
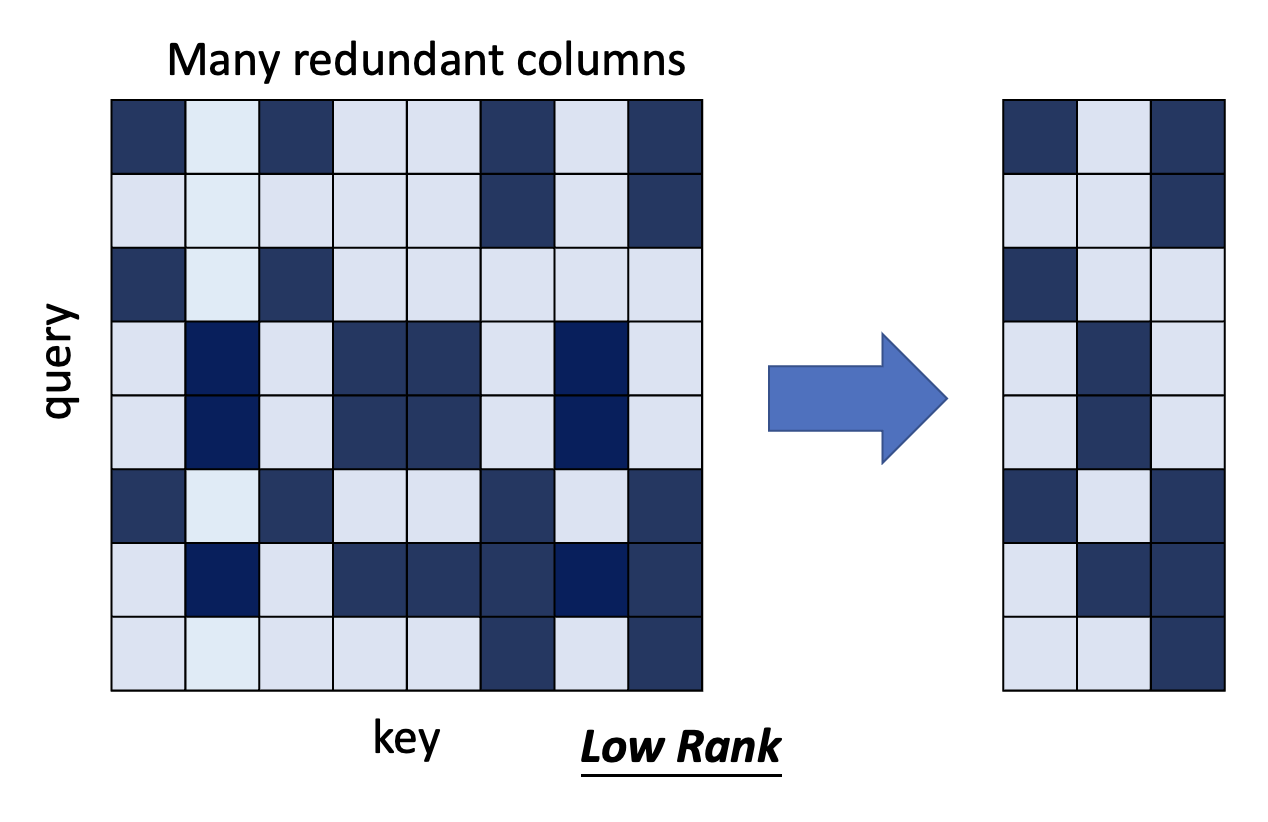
现在来思考一下:我们是否真的需要一个完整的注意矩阵吗?Linformer 这篇论文探讨了这个问题,发现注意矩阵的秩(rank) 并不大,也就是说不少列是相互依赖的,是冗余的,那么我们可以尝试将这些多余的列删掉,从而减小计算量。
注意矩阵的列对应的是键,所以我们从原来 \(N\) 个键中挑出一些具有代表性的键出来,共计 \(K\) 个。相应地,值的数量也要从 \(N\) 降至 \(K\) 个。
思考
能否减小查询的数量?
视情况而定。首先要注意的一点是:查询的数量决定了输出的数量。
- 有些任务(比如分类)可能只需要一个输出,这时可以尝试减小查询数量
- 但有的任务要求每个输入都要有对应的输出,那么不应该改变输出长度,此时就不得减小查询数量
那么具体该如何减小键的数量呢?下面给出一些方法:
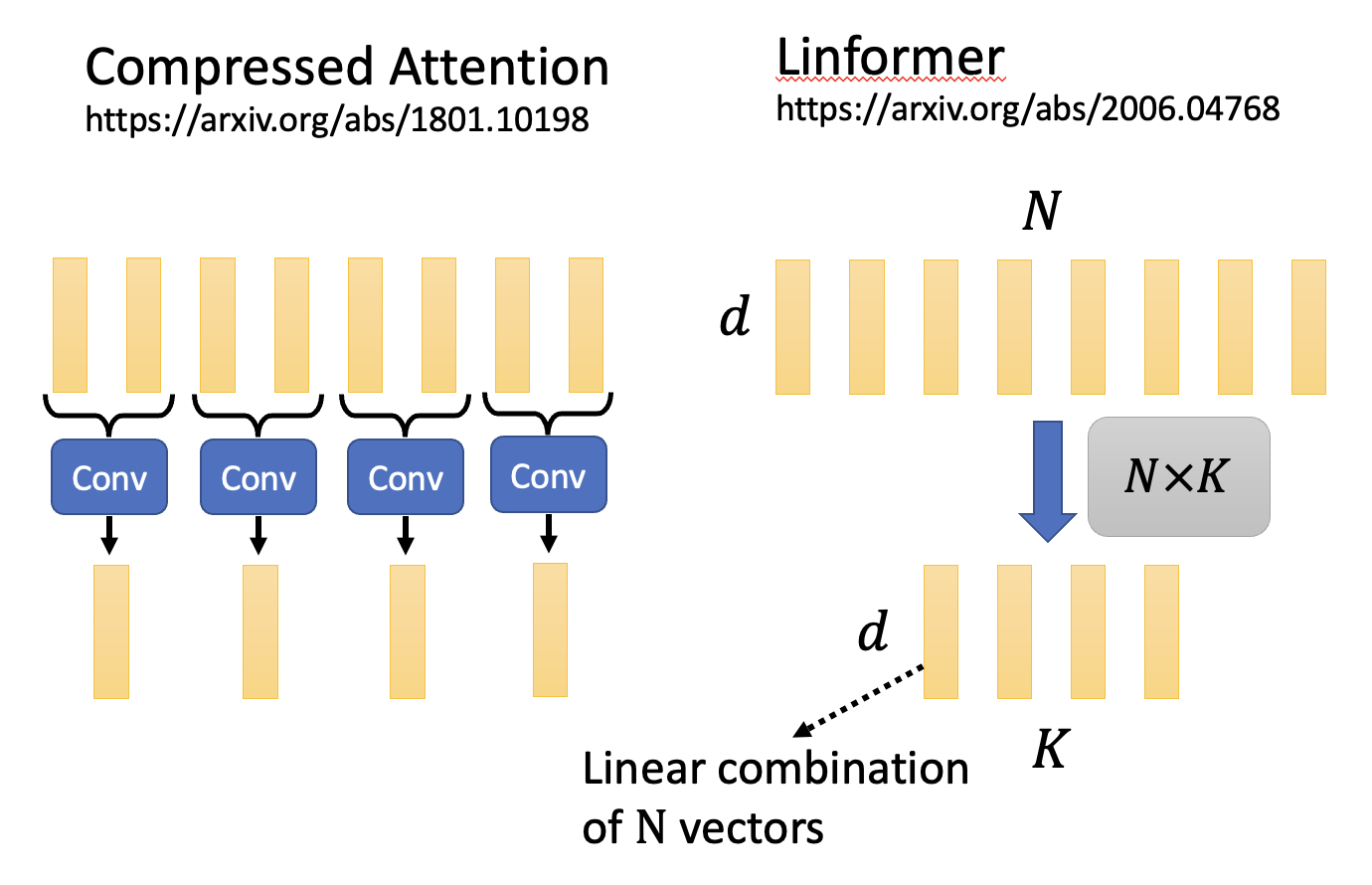
- 压缩注意(compressed attention):
- 采用 CNN,对整个序列扫描一遍,从而找出代表性的限量,缩短了序列长度
- Linformer:
- 将 \(N \times N\) 的注意矩阵和一个 \(N \times K\) 的矩阵相乘,从而得到让键的数量降至 \(K\) 个
- 实际上实现了 \(N\) 个向量的线性组合(linear combination)
Changing the Order of Matrix Multiplication⚓︎
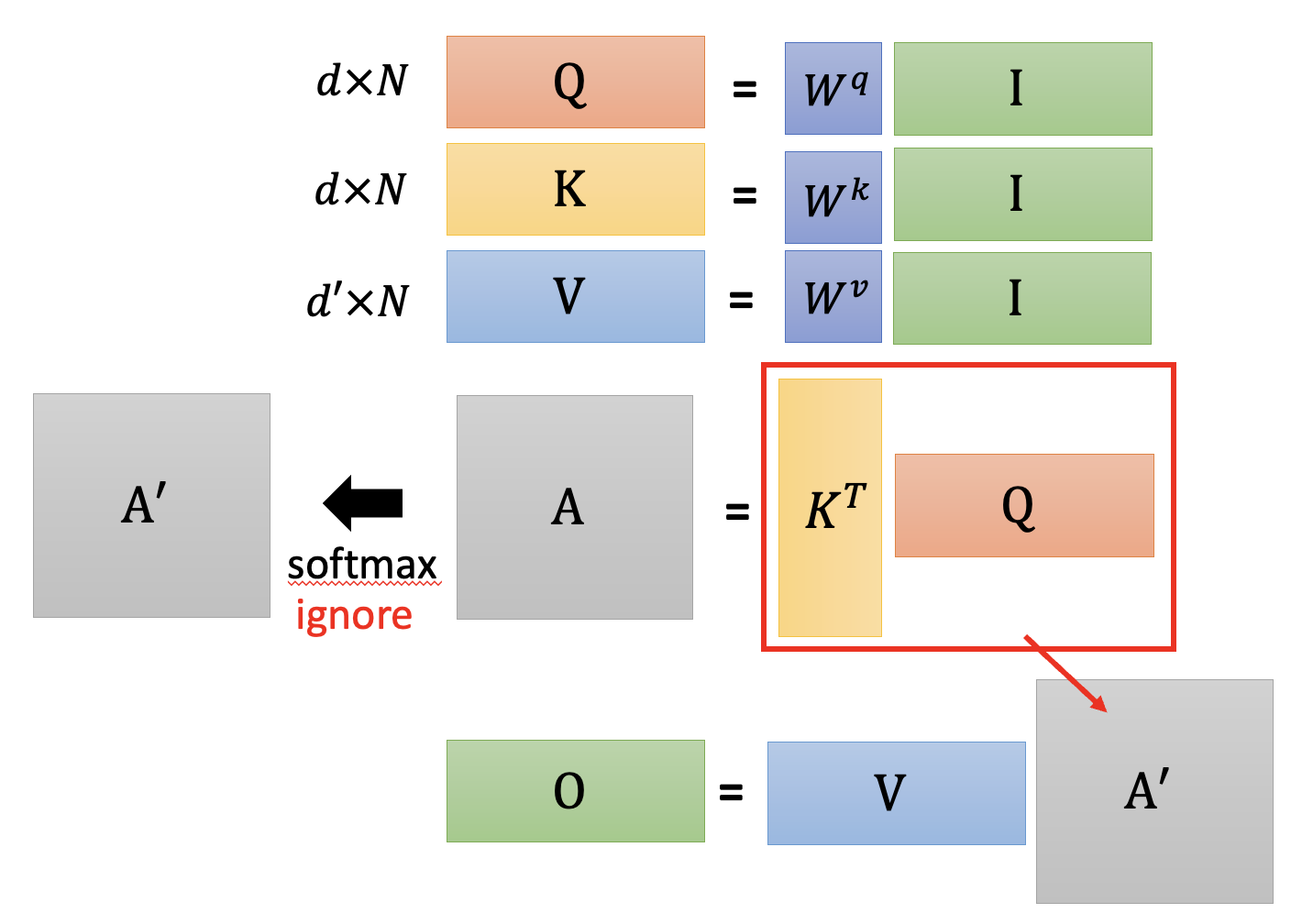
回顾一下:从数学层面上看,自注意机制本质上就是在做下面这样的矩阵乘法。
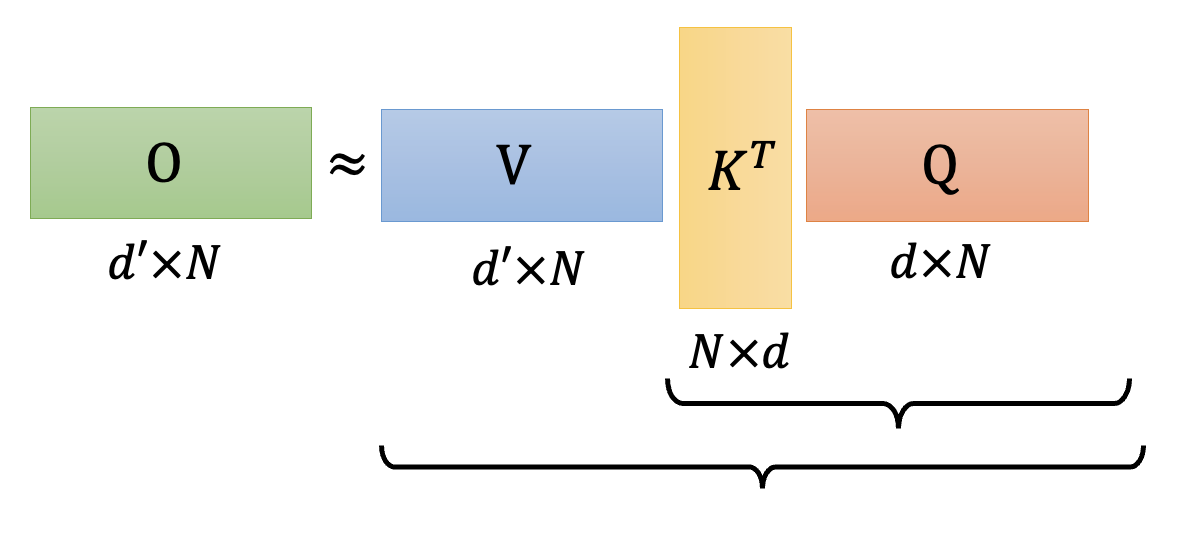
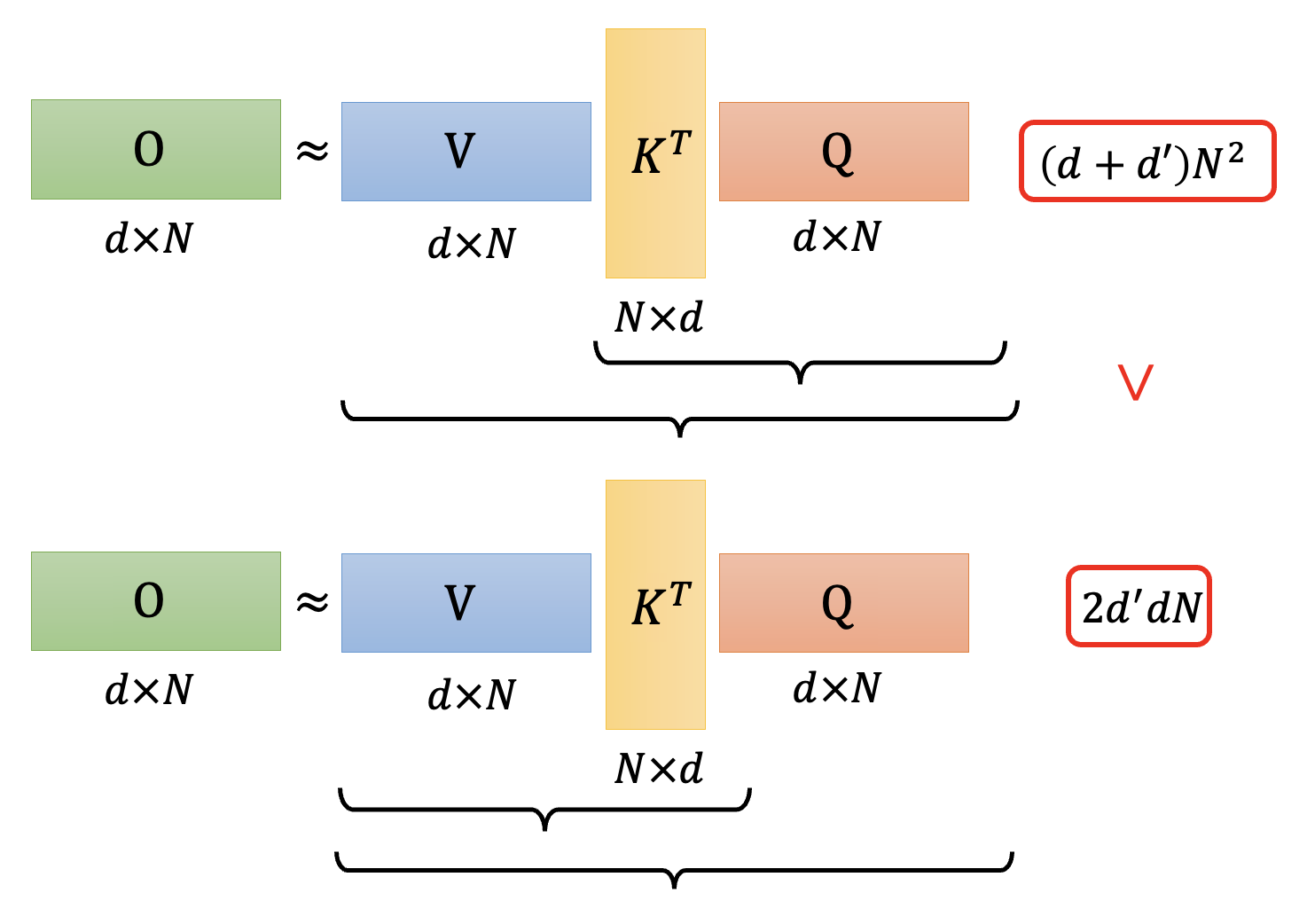
将最后一个矩阵乘法展开,我们发现实际上做的是一个三矩阵的乘法:
在 ADS 中,我们讨论过:选择适当的矩阵乘法顺序有时可以显著降低计算量(甚至能减小好几个量级
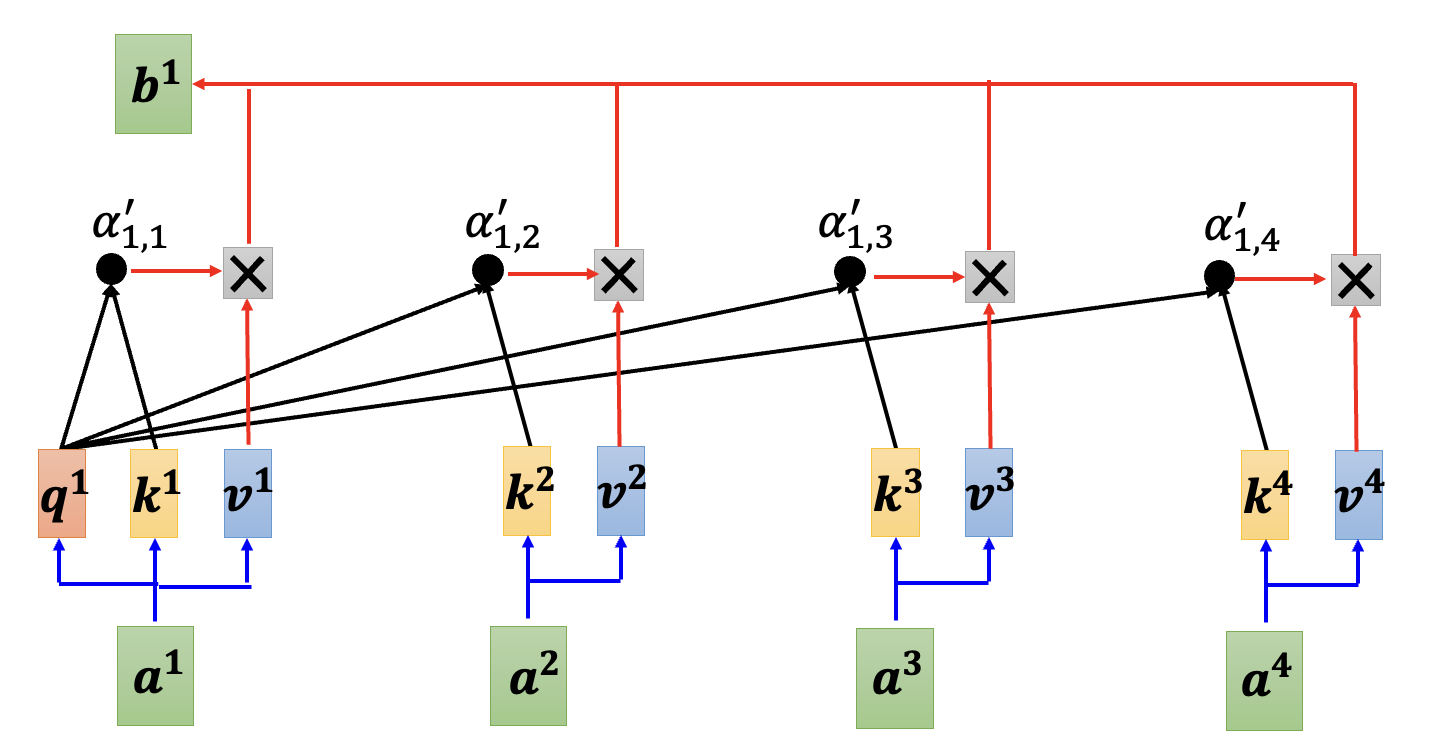
上图是原来的矩阵乘法,时间复杂度是 \(O(N^2)\) 的;下图就是改变顺序后的乘法,可以看到时间复杂度降至 \(O(N)\)。显然我们会采用下面这种乘法顺序,那么具体该怎么做呢?我们就从其中某个输出向量 \(\bm{b}^1\) 来分析——其计算公式为(用到了 softmax
继续展开这个计算公式:
-
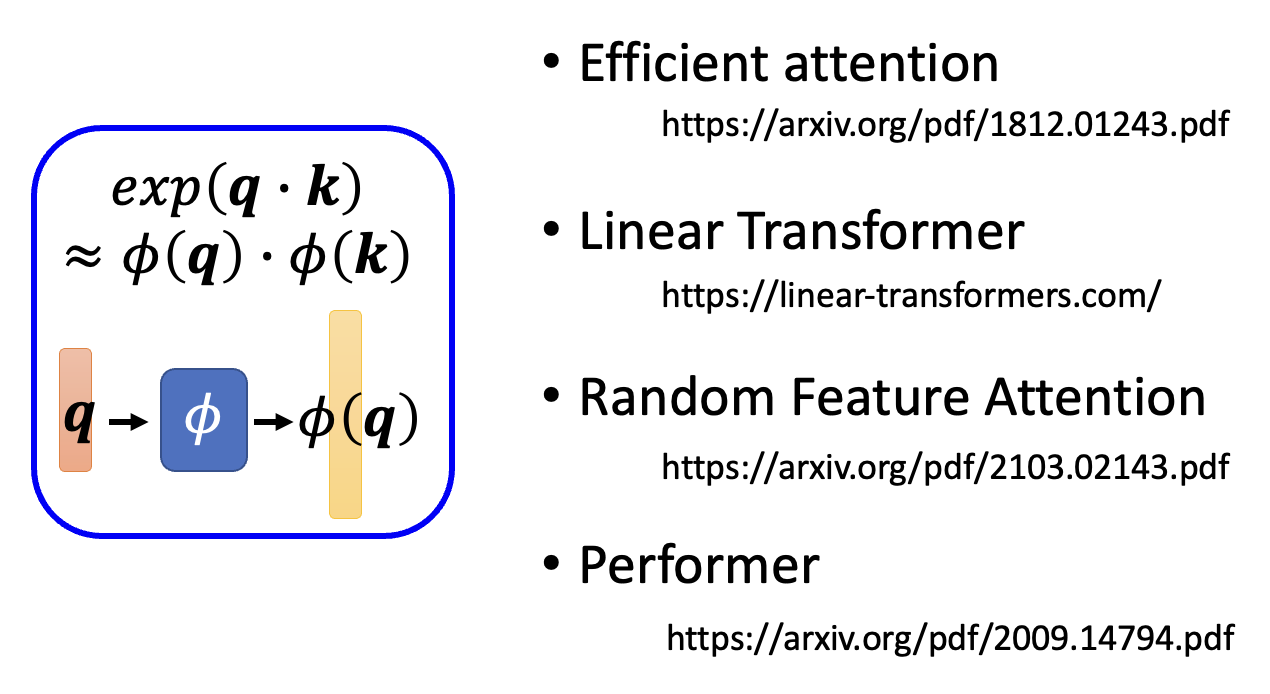
第一行到第二行,我们用了这样的公式: $$ \exp(\bm{q} \cdot \bm{k}) \approx \varphi(\bm{q}) \cdot \varphi(\bm{k}) $$
其中 \(\varphi()\) 是一个接收向量,输出也是向量的转换函数(暂时不用管具体是什么)
-
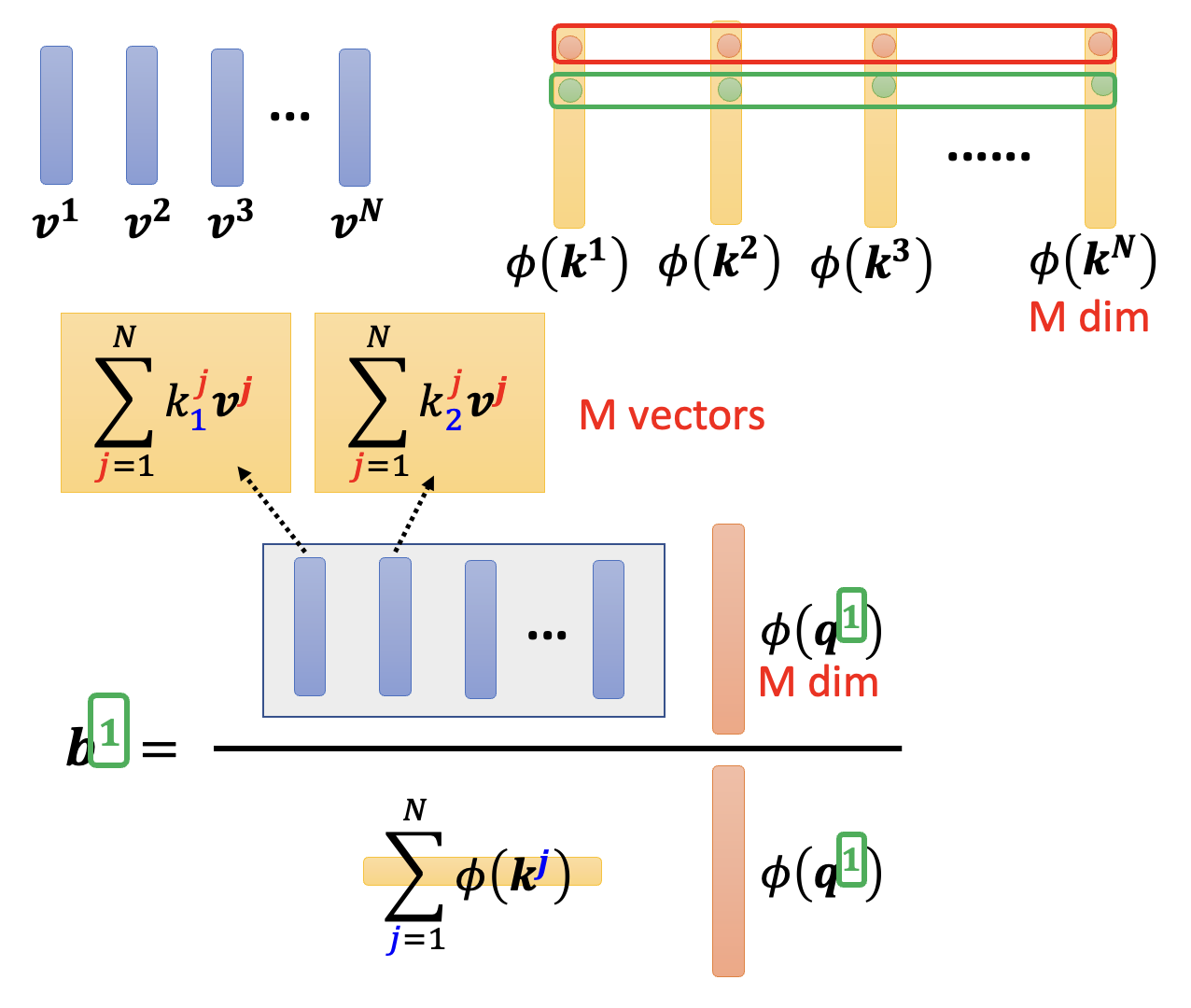
对于最后一行公式中的分母部分,还可以进一步转化为: $$ \varphi(\bm{q}^{\textcolor{green}{1}}) \cdot \sum_{\textcolor{cornflowerblue}{j}=1}^N \varphi(\bm{k}^{\textcolor{cornflowerblue}{j}}) $$
这实际上是一个向量乘法:
黄色部分就是 \(\sum_{\textcolor{cornflowerblue}{j}=1}^N \varphi(\bm{k}^{\textcolor{cornflowerblue}{j}})\),而红色则对应 \(\varphi(\bm{q}^{\textcolor{green}{1}})\)
-
再来看分子部分(下图蓝框框出来的公式
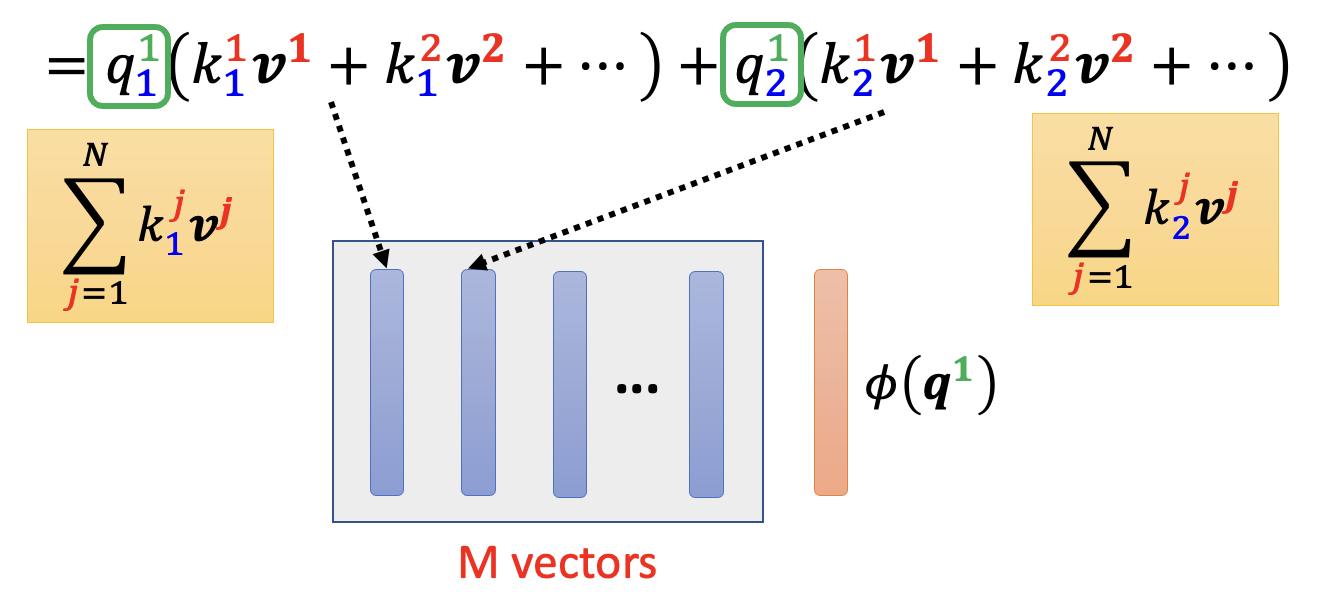
) ,我们可以像这样展开 >字太多了,不想打 \(\LaTeX\) 公式了,所以就直接贴个截图...用矩阵表示最后一行的式子(注意查询向量是 \(M\) 维的
) : -
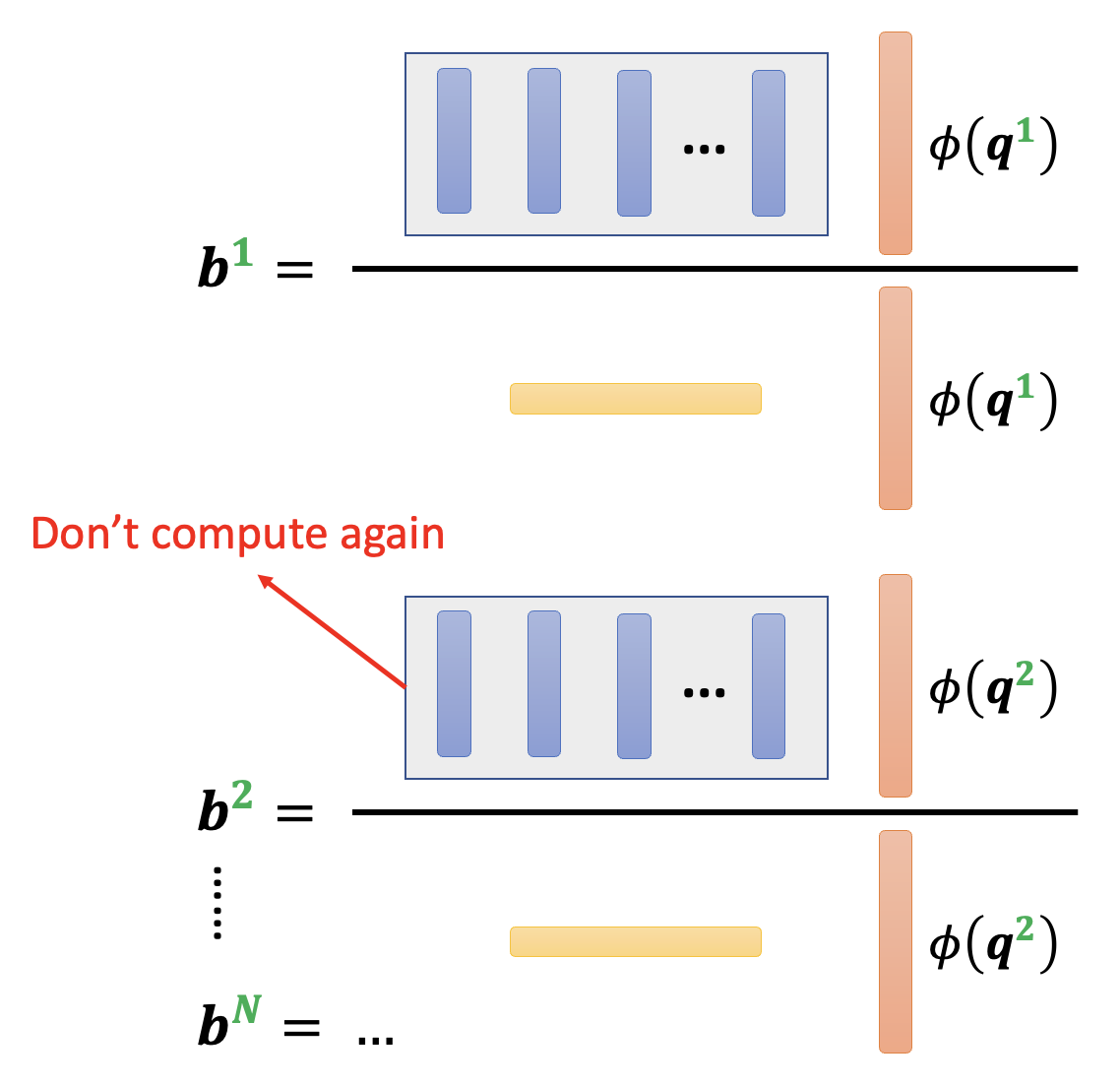
同时考虑分子分母,现在 \(\bm{b}^1\) 的计算变成了多个向量的乘除法了
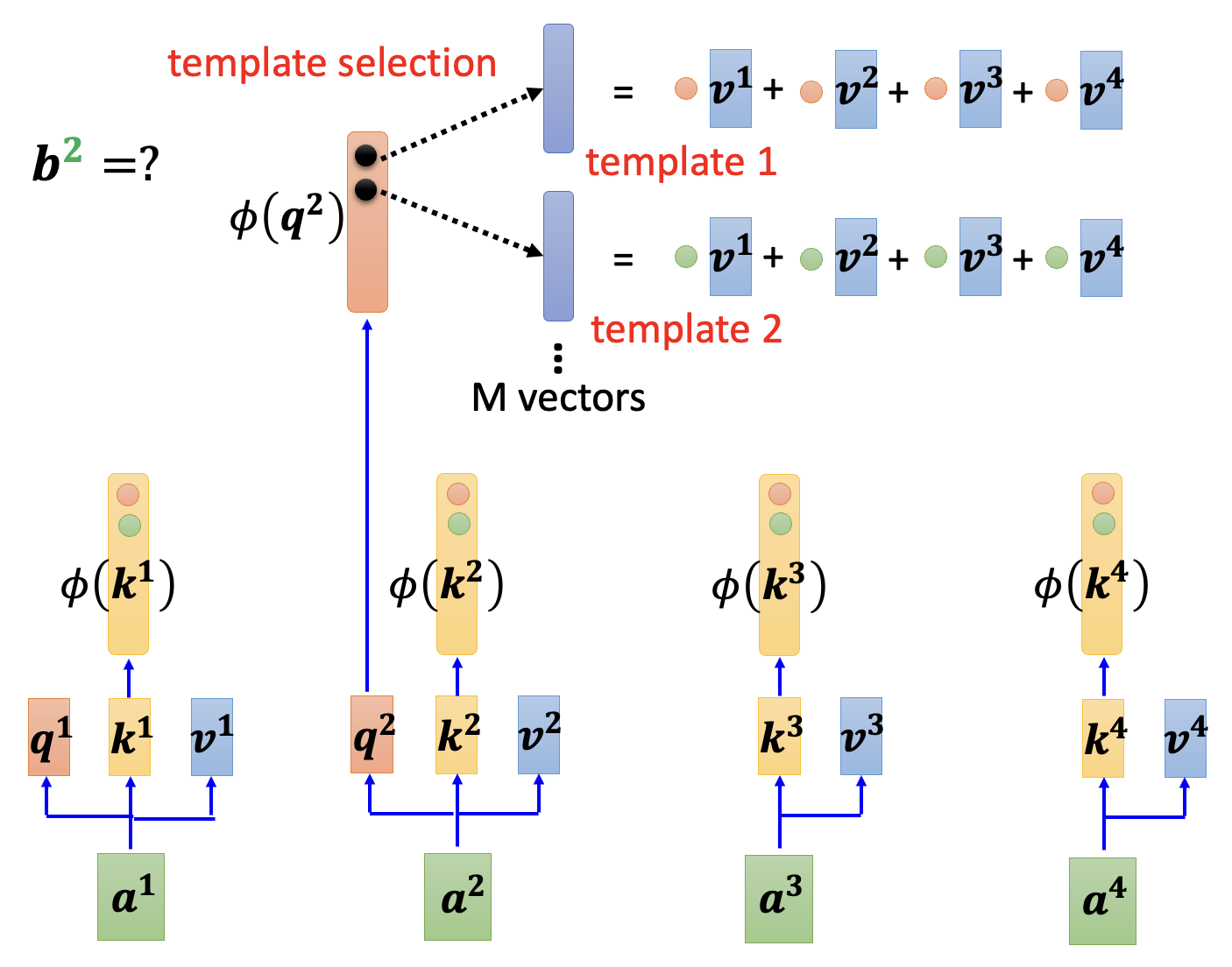
上面这种处理的好处是:图中灰色方框和黄色方框对应的部分仅需计算一次,之后计算输出向量时就可以复用这些结果,从而减小计算量。
其中灰色方框内的 \(M\) 个向量(蓝色方块)称为模板(template)。
关于函数 \(\varphi()\) 的具体实现,可以参考以下几篇 paper:
Synthesizer⚓︎
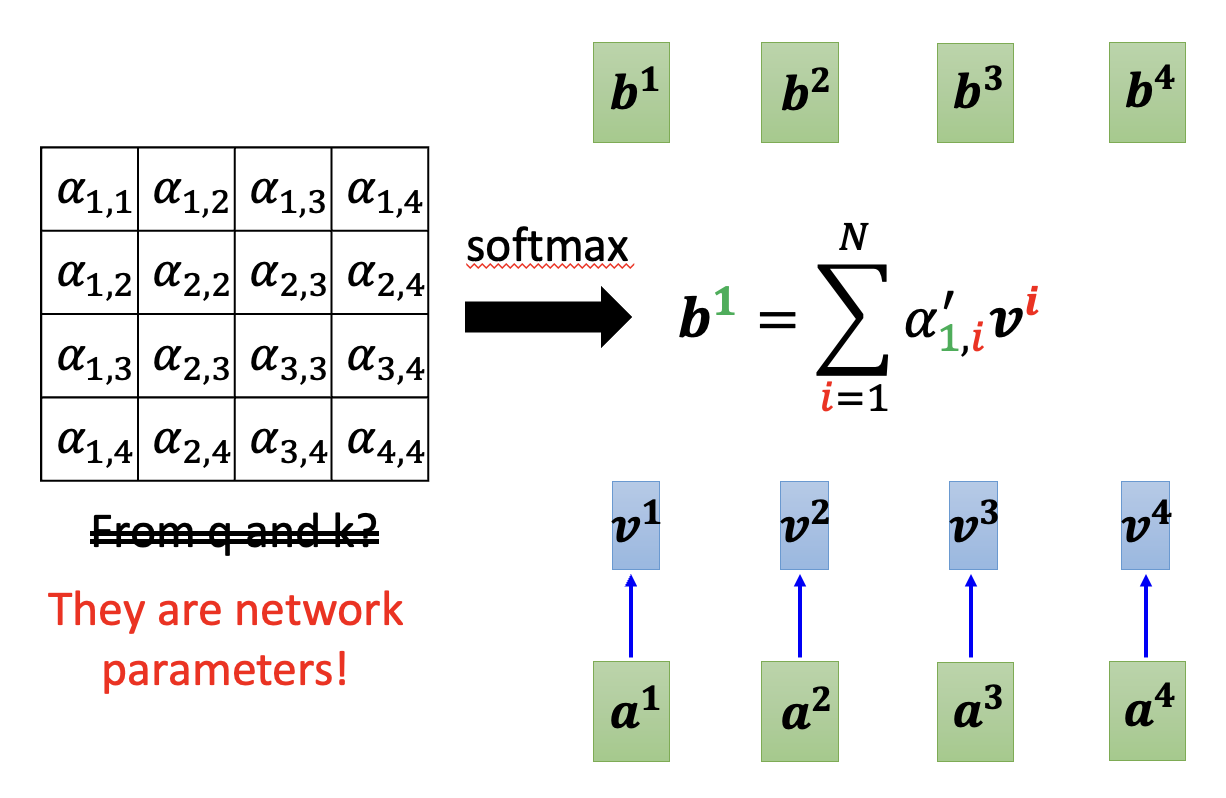
我们还可以再脑洞大开一点——计算自注意的时候一定要先算出查询和键吗?一种称为合成器(synthesizer) 的技术就跳过这个步骤——它的注意权重作为网络参数,是从模型中学出来的(和 Sinkhorn 排序网络很像
Attention-free Techniques⚓︎
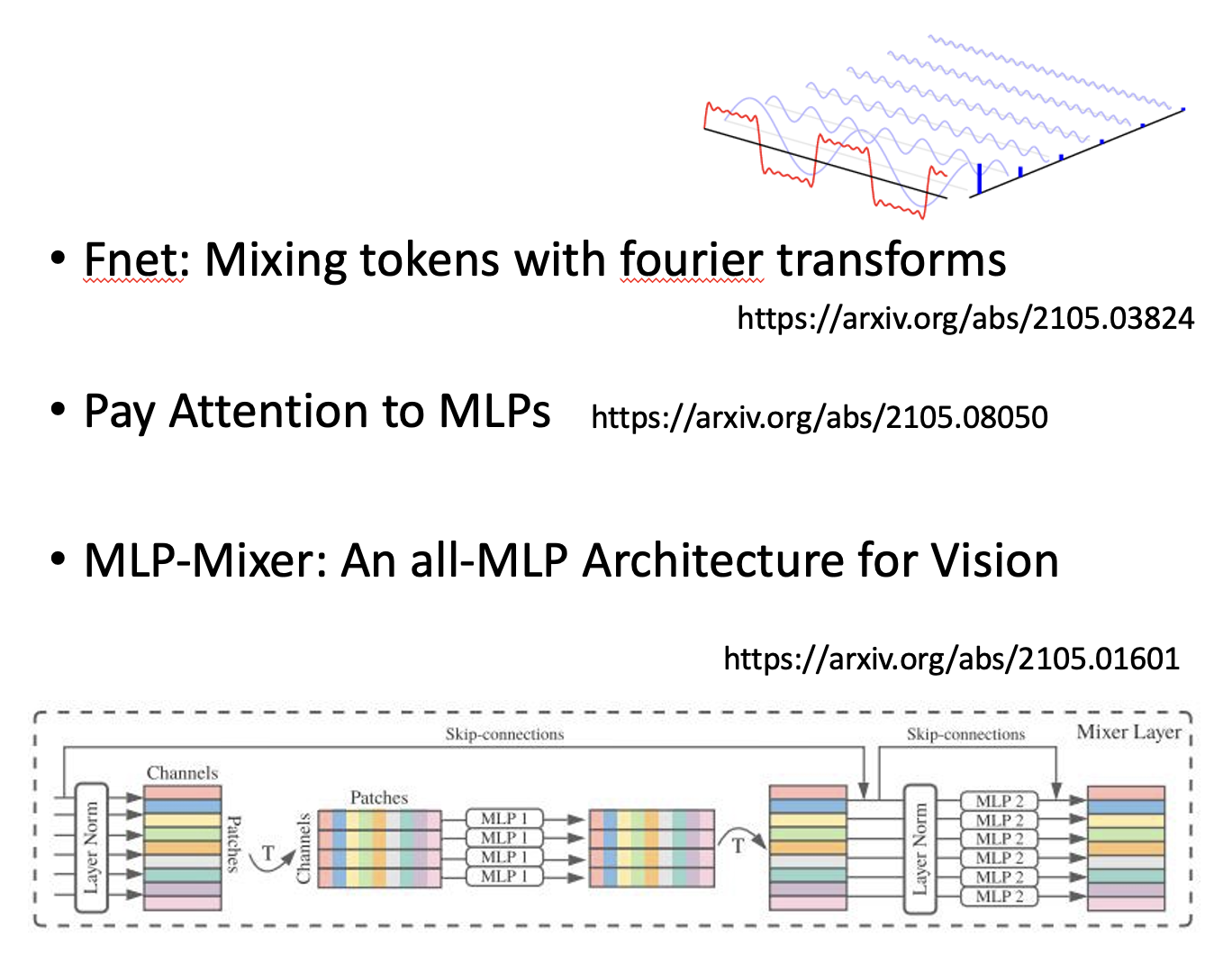
更进一步思考——处理序列的模型非要用到自注意机制吗?下面是一些尝试丢掉自注意机制的方案:
评论区