第 1 章 概率论的基本概念⚓︎
约 2119 个字 预计阅读时间 11 分钟
核心知识
- 一些基本概念
- 条件概率、乘法公式、全概率公式、贝叶斯公式
- 独立事件
样本空间,随机事件⚓︎
概念⚓︎
随机试验的特点:
- 可以在相同的条件下重复进行
- 每次试验可能出现的结果是不确定的,但能事先知道试验的所有可能结果
- 每次试验完成前不能预知哪一个结果会发生
- 样本空间 \(S\):随机试验的所有可能结果构成的集合,包括:
- 有限样本空间
- 无限样本空间
- 可数(与自然数集一一对应)
- 不可数(任意实数区间)
- 样本点:随机试验的每一个结果
- 随机事件(简称事件
) :样本空间的任一子集 - 基本事件:只含有一个样本点的事件
- 事件发生:试验所出现的结果(即样本点)属于某一事件,即这一事件所包含的样本点恰好为此次试验的结果
- 样本空间可视为一事件,这样的事件必定发生,被称为必然事件
- 空集 \(\emptyset\) 也可视为一事件,被称为不可能事件
基本运算⚓︎
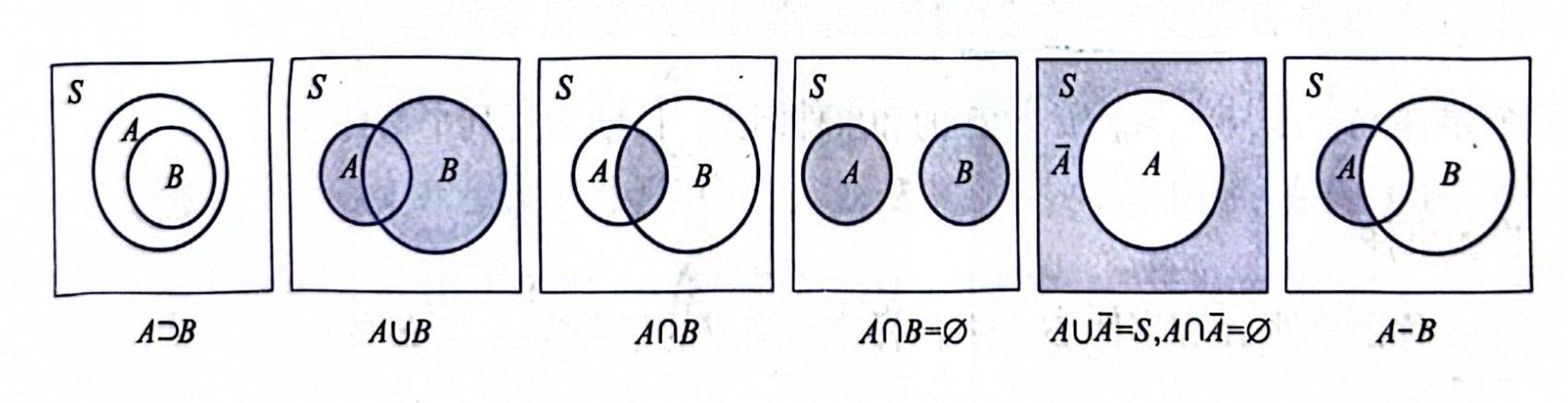
- 包含 / 包含于:\(A \supset B/B \subset A\)
- 相等:\(A = B \Leftrightarrow (A \subset B) \wedge (B \subset A)\)
- 和事件:\(A \cup B = \{x: x \in A \ \mathrm{or}\ x \in B\}\)
- 有限个事件:\(\bigcup\limits_{i=1}^n A_i\)
- 无限个事件:\(\bigcup\limits_{i=1}^{+\infty} A_i\)
- 积事件:\(A \cap B = AB = \{x: x \in A \ \mathrm{and}\ x \in B\}\)
- 有限个事件:\(\bigcap\limits_{i=1}^n A_i\)
- 无限个事件:\(\bigcap\limits_{i=1}^{+\infty} A_i\)
- 互不相容 / 互斥:\(A \cap B = \emptyset\)
- 逆事件 / 对立事件:\((A \cap B = \emptyset) \wedge (A \cup B = S)\),其中事件 \(B\) 记作 \(\overline{A}\),即 \(\overline{A} = \{x: x \notin A\}\)
- 差事件:\(A - B = A \cap \overline{B} = \{x: x \in A \wedge x \notin B\}\)
维恩图:
运算规则:
- 交换律:
- \(A \cup B = B \cup A\)
- \(A \cap B = B \cap A\)
- 结合律
- \(A \cup (B \cup C) = (A \cup B) \cup C\)
- \(A \cap (B \cap C) = (A \cap B) \cap C\)
- 分配律
- \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
- \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)
- 德摩根定律
- \(\overline{\bigcup\limits_{j=1}^n A_j} = \bigcap\limits_{j=1}^n \overline{A_j}\)
- \(\overline{\bigcap\limits_{j=1}^n A_j} = \bigcup\limits_{j=1}^n \overline{A_j}\)
频率与概率⚓︎
频率⚓︎
- 频数 \(n_A\):事件 \(A\) 在 \(n\) 次重复试验中发生的次数(\(0 \le n_A \le n\))
- 频率 \(f_n(A) = \dfrac{n_A}{n}\)
频率的性质:
- 对任一事件 \(A\),\(0 \le f_n(A) \le 1\)
- \(f_n(S) = 1\)
- 若 \(A \cap B = \emptyset\),则 \(f_n(A \cup B) = f_n(A) + f_n(B)\)
- 扩展版:若 \(A_1, A_2, \dots, A_k(k \ge 3)\) 两两互斥时, $$ f_n(\bigcup\limits_{j=1}^k A_j) = \sum\limits_{j=1}^kf_n(A_j) $$
概率⚓︎
- 定义 1:\(A\) 的频率 \(f_n(A)\) 的稳定值 \(p\) 被认为是事件 \(A\) 的概率。
-
定义 2:设样本空间 \(S\) 的任一事件 \(A\),定义一个实数 \(P(A)\),若它满足以下三条公理:
- 非负性:\(P(A) \ge 0\)
- 规范性:\(P(S) = 1\)
- 可列可加性:对 \(S\) 中可列个两两互斥的事件 \(A_1, A_2, \dots, A_n, \dots\)(即 \(A_iA_j=\emptyset, i \ne j, i, j = 1, 2, \dots\)
) ,有 \(P(\bigcup\limits_{j=1}^{+\infty}A_j) = \sum\limits_{j=1}^{+\infty}P(A_j)\)
则称 \(P(A)\) 为事件 \(A\) 发生的概率。
根据定义 2,可以引申出以下性质:
- 有限可加性:对于有限个两两互斥的事件,有 \(P(\bigcup\limits_{j=1}^{n}A_j) = \sum\limits_{j=1}^{n}P(A_j)\)
- \(P(A) = 1 - P(\overline{A})\)
- \(P(\emptyset) = 0\)
- 当 \(A \supset B\) 时,\(P(A-B) = P(A) - P(B) \Rightarrow P(A) \ge P(B)\)
- 对于一般情况,\(P(A - B) = P(A) - P(AB)\)
- \(P(A) \le P(S) = 1\)
-
\(P(A \cup B) = P(A) + P(B) - P(AB)\)
- 推广(容斥原理
) :
\[ \begin{align} P(\bigcup\limits_{j=1}^n A_j) = & \sum\limits_{j=1}^nP(A_j) - \sum\limits_{i < j}(A_iA_j) + \sum\limits_{i < j < k}P(A_iA_jA_k) - \dots + \notag \\ & (-1)^{n-1}P(A_1A_2 \dots A_n),\quad n \ge 1 \notag \end{align} \] - 推广(容斥原理
等可能概型⚓︎
一个随机试验,如果满足下列性质:
- 有限性:样本空间的样本点数有限
- 等可能性:每一个样本点出现的概率相等
那么称这个试验为等可能概型 / 古典概型
若样本空间为 \(S = \{e_1, e_2, \dots, e_n\}(n \ge 1)\),随机事件 \(A = \{e_{i_1}, e_{i_2}, \dots, e_{i_l}\}\),其中 \(i_1, \dots, i_l\) 是 \(1, 2, \dots, n\) 中某 \(l(l \ge 1)\) 个不同的值,则:
例题
实际推断原理:概率很小的事件,在一次试验中几乎是不可能发生的。
条件概率⚓︎
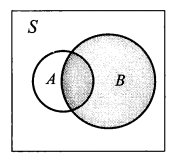
条件概率的定义:如果 \(P(B) > 0\),那么在 \(B\) 发生的情况下 \(A\) 发生的条件概率为:
可以将条件概率 \(P(A|B)\) 理解为在缩小的样本空间\(B\) 内,事件 \(A\) 发生的概率,下面用维恩图表示这种条件概率:
条件概率相关的性质(假定 \(P(C) \ne 0\)
- \(P(A|C) \ge 0\)
- \(P(S|C) = 1\)
- \(P(B|C) = 1 - P(\overline{B}|C)\)
- 当 \(A \supset B\) 时,\(P(A|C) \ge P(B|C)\)
- \(P(A \cup B | C) = P(A|C) + P(B|C) - P(AB|C)\)
- 特别地,若 \(AB = \emptyset\),则 \(P(A \cup B | C) = P(A|C) + P(B|C)\)
例题
乘法公式⚓︎
当 \(P(A) \ne 0, P(B) \ne 0\) 时,称下面的等式为乘法公式:
推广到 n 个事件:当 \(P(A_1A_2 \dots A_{n-1}) \ne 0(n \ge 3)\) 时,有:
在条件概率中,乘法公式依然成立(\(P(AC) \ne 0\)
全概率公式、贝叶斯公式⚓︎
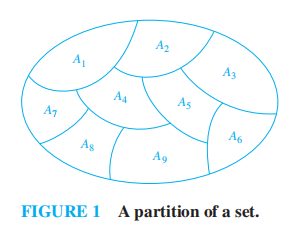
设 \(S\) 为某一随机试验的样本空间,\(B_1, B_2, \dots, B_n\) 为该试验的一组事件,且满足:
- 不重:\(B_iB_j = \emptyset, i, j = 1, 2, \dots, n, i \ne j\)
- 不漏:\(B_1 \cup B_2 \cup \dots \cup B_n = S\)
则称 \(B_1, B_2, \dots, B_n\) 为 \(S\) 的一个划分(或完备事件组)
注:离散数学“Relations”一章提到过这个概念哦 ~(
所以直接从离散数学那边挖一张图过来)
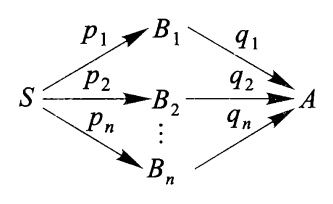
全概率公式:设 \(S\) 为某一试验的样本空间,若 \(B_1, B_2, \dots, B_n\) 是 \(S\) 的一个划分,且 \(P(B_j) > 0, j = 1, 2, \dots, n\),则对任一事件 \(A\),有
设 \(P(B_j) = p_j\),\(P(A|B_j) = q_j, j = 1, 2, \dots, n\),则 \(P(A) = \sum\limits_{j=1}^np_jq_j\),对应的图示分析如下,看上去会更加直观:
贝叶斯 (Bayes) 公式(逆概公式
在贝叶斯公式中,\(P(B_j)(j = 1, 2, \dots, n)\) 往往是已知或事先假设的,因此被称为先验概率;而当事件 \(A\) 发生后,对 \(B_j\) 发生的概率重新进行推断或修正,因此称 \(P(B_j|A)\) 为后验概率。
事件的独立性与独立检验⚓︎
设 \(A, B\) 为两随机事件,当
时,称事件 \(A, B\)相互独立。当 \(P(A) \cdot P(B) \ne 0\) 时,事件 \(A, B\) 相互独立等价于条件概率 = 无条件概率,即
若 \(A, B\) 相互独立,则 \(A\) 与 \(\overline{B}\),\(\overline{A}\) 与 \(B\),\(\overline{A}\) 与 \(\overline{B}\) 相互独立。
推广:
-
设 \(A, B, C\) 为三个随机事件,当
\[ \begin{align} P(AB) & = P(A)P(B) \notag \\ P(AC) & = P(A)P(C) \notag \\ P(BC) & = P(B)P(C) \notag \end{align} \]均成立时,称事件 \(A, B, C\)两两独立,若同时还满足
\[ P(ABC) = P(A)P(B)P(C) \]则称事件 \(A, B, C\)相互独立。
注意
相互独立 \(\Rightarrow\) 两两独立,但两两独立 \(\not \Rightarrow\) 相互独立
-
设 \(n\) 个事件 \(A_1, A_2, \dots, A_n(n \ge 2)\),若对其中任意 \(k\) 个事件 \(A_{i_1}, A_{i_2}, \dots, A_{i_k}\),都有
\[ P(A_{i_1}, A_{i_2}, \dots, A_{i_k}) = \prod\limits_{j = 1}^kP(A_{i_j}) \]成立,则称事件 \(A_1, A_2, \dots, A_n\)相互独立。
- 独立试验:试验结果互不影响的一系列试验
- 重复试验:各个子试验是在相同条件下进行的
评论区