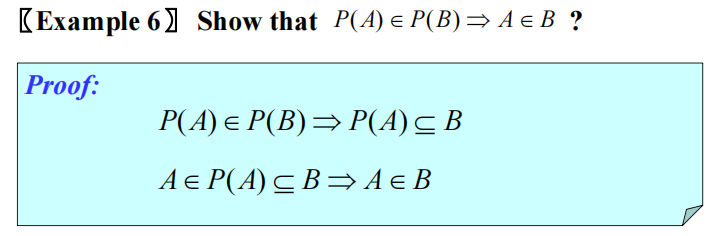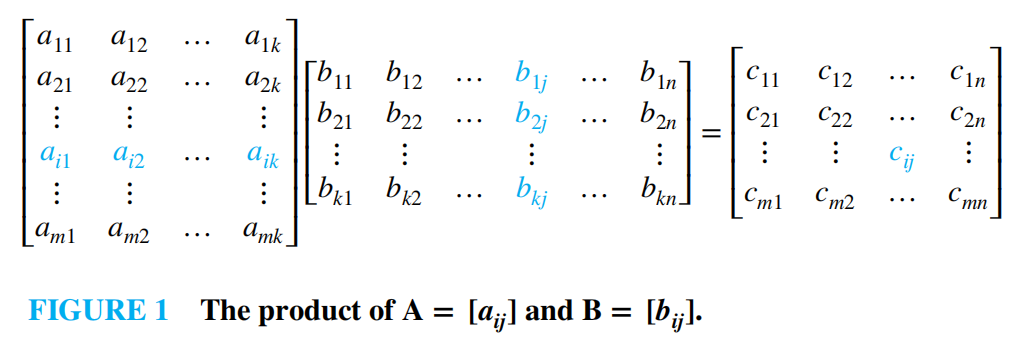Chap 2 Basic Structures: Sets, Functions, Sequences, Sums, and Matrices⚓︎
约 5409 个字 预计阅读时间 27 分钟
核心知识
- 集合
- 一些基本概念
- 基数:集合元素个数
- 有限集
- 无限集:可数与不可数
- 幂集
- 笛卡尔积
- 集合的运算:并、交、补、差、对称差 ...
- 恒等式(类似逻辑等值)
- 函数
- 单射、满射、双射
- 反函数、复合函数
- 底函数、顶函数
- 序列
- 递推关系
- 矩阵(关系和图论里会频繁用到)
Sets⚓︎
Introduction⚓︎
集合 (set):一组拥有不同对象(被称为元素 (element))的无序集
- \(a \in A\):\(a\) 是 \(A\) 中的一个元素
- \(a \notin A\):\(a\) 不是 \(A\) 中的一个元素
注:
- 一般大写字母表示集合,小写字母表示元素
- 集合也可以作为某个集合的元素
- 集合不关注元素的顺序和重复
The Description of Sets⚓︎
1. 枚举法 (roster method):用花括号 { } 包含所有元素,比如 \(S = \{a, b, c, d\}\)
如果元素个数太多,可用省略号 (ellipses)(...) 表示
2. set builder:\(\{x | x \text{ has property }P\}\),对于集合中的所有 \(x\) 元素,都具有 \(P\) 性质
数学中常用的一些集合:
- 自然数集 \(\mathbb{N} = \{0, 1, 2, 3, \dots \}\)
- 整数集 \(\mathbb{Z} = \{\dots, -2, -1, 0, 1, 2 \dots \}\)
- 正整数集 \(\mathbb{Z^+} = \{1, 2, 3, \dots\}\)
- 有理数集 \(\mathbb{Q} = \{\dfrac{p}{q} | p \in \mathbb{Z}, q \in \mathbb{Z}, \text{and } q \ne 0\}\)
- 实数集 \(\mathbb{R}\), 正实数集 \(\mathbb{R^+}\)
- 复数集 \(\mathbb{C}\)
3. 区间 (intervals):
- 闭区间 (closed interval):\([a, b] = \{ x | a \le x \le b \}\)
- 开区间 (open interval):\((a, b) = \{ x | a < x < b\}\)
- 还有:\([a, b) = \{x | a \le x < b\} \quad (a, b] = \{x | a < x \le b\}\)
注:在 CS 中,数据类型 (datatype) 也是一种集合,同时也包含了一些运算的集合
相等:\(A = B\),当且仅当 \(\forall x(x \in A \leftrightarrow x \in B)\),或者 \((A \subseteq B) \wedge (B \subseteq A)\)
空集 (empty Set/ null Set):没有元素的集合,用 "\(\emptyset\)" 表示
单元素集合 (singleton set):只有一个元素的集合
注意:\(\emptyset \ne \{\emptyset\}\)
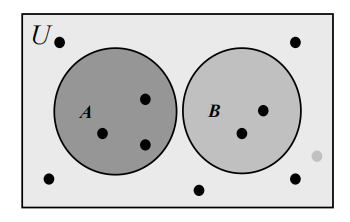
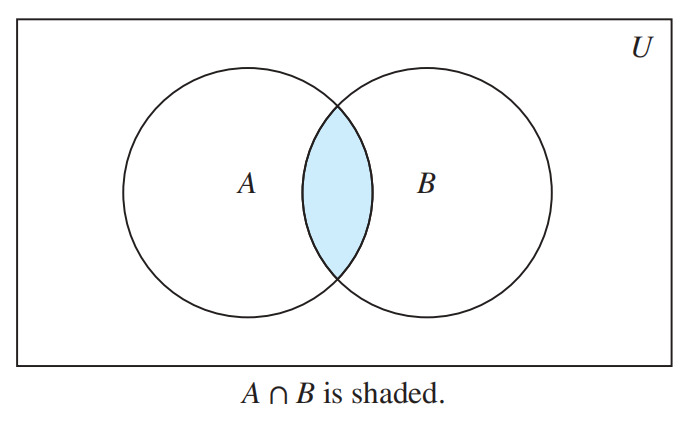
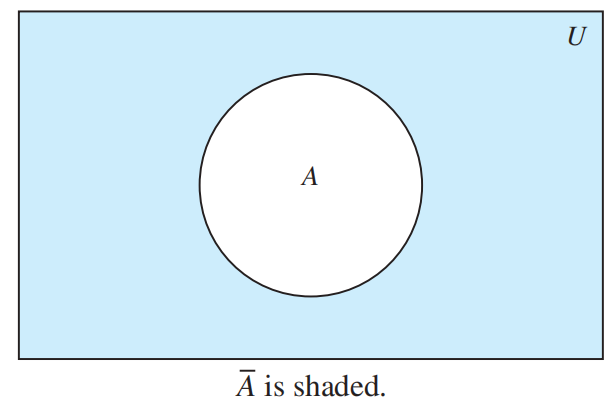
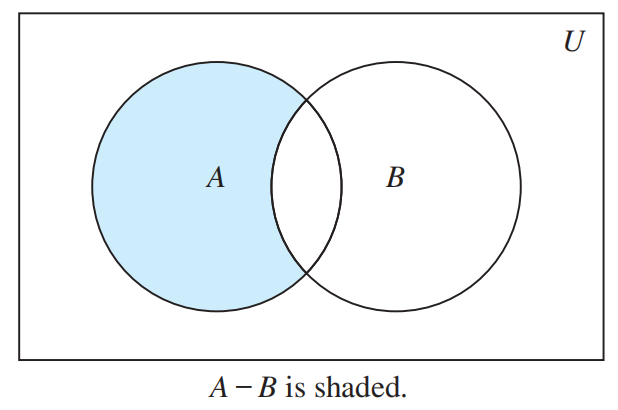
Veen Diagram⚓︎
细节:
- 用矩形表示全集 (universal Set)\(U\)
- 矩形中的每个圆圈表示集合
- 用点表示元素
Subsets⚓︎
\(A\) 是 \(B\) 的子集 (subset) = \(B\) 是 \(A\) 的超集 (superset),即 \(A\) 中的每个元素都是 \(B\) 的元素
记号:\(A \subseteq B\) 或 \(B \supseteq A\),等价于 \(\forall x(x \in A \rightarrow x \in B)\)
- 如何说明 \(A \subseteq B\):说明每个属于 A 的元素也属于 B
- 如何说明 \(A \nsubseteq B\):找到一个元素 \(x\),使得 \(x \in A\) 但 \(x \notin B\)
定理:对于每个集合 \(S\),\(\text{(i)} \emptyset \subseteq S \quad \text{(ii)} S \subseteq S\)
真子集 (proper subset):\(A\) 是 \(B\) 的子集,但 \(A \ne B\),记作 \(A \subset B\)。
也就是说,\(\forall x(x \in A \rightarrow x \in B) \wedge \exists x(x \in B \wedge x \notin A)\)
The Size of a Set⚓︎
如果 \(S\) 有 \(n\) 个不同的元素,称 \(S\) 为有限集 (finite Set),且 \(n\) 是 \(S\) 的基数 (cardinality),记作 \(|S|\);否则认为该集合是无限的 (infinite)
基数的概念在后面会详细介绍
Power Sets⚓︎
幂集合 (power Sets):包含集合 \(S\) 的所有子集的集合,记作 \(P(S) = \{x | x \subseteq S\}\) 如果集合有\(n\)个元素,则它对应的幂集合有\(2^n\)个元素
性质:
- \(P(A) \in P(B) \rightarrow A \in B\)
- \(P(A) \subseteq P(B) \leftrightarrow A \subseteq B\)
Cartesian Products⚓︎
有序 n 元组 (The ordered n-tuple)\((a_1, a_2, \dots, a_n)\) $$ (a_1, a_2, \dots, a_n) = (b_1, b_2, \dots, b_n) \Leftrightarrow a_i = b_i(i = 1, 2, \dots, n) $$
有序对 (Ordered pairs):\(n = 2\) 的有序 n 元组
注意:\((a, b) \ne (b, a)\),除非 \(a = b\)
笛卡尔积 (Cartesian Products):\(A \times B = \{(a, b) | a \in A \wedge b \in B\}\)
对于多个集合的笛卡尔积:
当 \(A_1 = A_2 = \dots = A_n = A\) 时,
性质:
- 如果 \(|A| = m, |B| = n\),那么 \(|A \times B| = |B \times A| = mn\)
- \(A \times B \ne B \times A\),除非 \((A = \emptyset) \vee (B = \emptyset) \vee (A = B)\)
- \((A \times B) \times C \ne A \times B \times C\)
- \(A \times \emptyset = \emptyset \times A = \emptyset\)
- \((x, y) \in A \times B \Rightarrow x \in A \wedge y \in B \quad \quad (x, y) \notin A \times B \Rightarrow x \notin A \vee y \notin B\)
Using Set Notation with Quantifiers⚓︎
Truth Sets and Quantifiers⚓︎
真值集 (truth sets)\(P\) 是指对于某个域 \(D\) 的所有 \(x\),都有 \(P(x)\) 为真,即 \(\{x \in D|P(x)\}\)
- 当且仅当它的真值集 \(P\) 为集合 \(U\) 时,\(\forall xP(x)\) 在全集域 \(U\) 为真
- 当且仅当它的真值集 \(P\) 非空时,\(\exists xP(x)\) 在全集域 \(U\) 为真
Supplements(from Exercises)⚓︎
罗素悖论 (Russell's paradox):\(S = \{ x | x \notin x\}\)
经典例子:理发师悖论
Set Operations⚓︎
Set Operations⚓︎
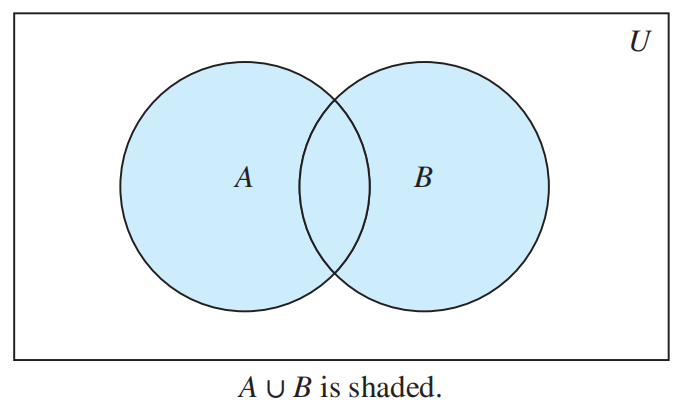
- 并集 (union):\(A \cup B = \{x|x \in A \vee x \in B\}\)
一些小结论
- \(A \subseteq A \cup B, \quad B \subseteq A \cup B\)
- \(A \subseteq C, B \subseteq C \Rightarrow A \cup B \subseteq C\)
- \(|A \cup B| \le |A| + |B|\)
- \(A \cup B = B \Leftrightarrow A \subseteq B\)
- 交集 (intersection):\(A \cap B = \{x|x \in A \wedge x \in B\}\)。如果 \(A \cap B = \emptyset\),被称为不相交 (disjoint) 集。
一些小结论
- \(A \cap B \subseteq A, \quad A \cap B \subseteq B\)
- \(C \subseteq A, C \subseteq B \Rightarrow C \subseteq A \cap B\)
- \(|A \cap B| \le |A|, \quad |A \cap B| \le |B|\)
- \(A \cap B = A \Leftrightarrow A \subseteq B\)
- 补集 (complement):在全集 \(U\) 中,集合 \(A\) 的补集为 \(\overline{A}\),它是关于 \(U\) 的 \(A\) 的补,即 \(U - A\). \(\overline{A} = \{x \in U | x \notin A\}\)
- 差集 (difference):\(A - B = \{x | x \in A \wedge x \notin B\} = A \cap \overline{B}\)
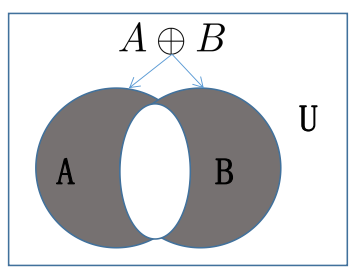
- (补充)对称差集 (symmetric difference):\(A \oplus B = (A \cup B) - (A \cap B) = (A - B) \cup (B - A)\)
注:本质上就是异或 (xor)
一些小结论
- \(A \oplus A = \emptyset \quad A \oplus \emptyset = A \quad A \oplus U = \overline{A} \quad A \oplus \overline{A} = U\)
- \(A \oplus B = B \oplus A \quad (A \oplus B) \oplus B = A\)
- \((A \oplus B) \oplus C = A \oplus (B \oplus C)\)
More on Set Cardinality⚓︎
⭐容斥原理 (The Principle of Inclusion-Exclusion):
注:Chap 8 会详细介绍
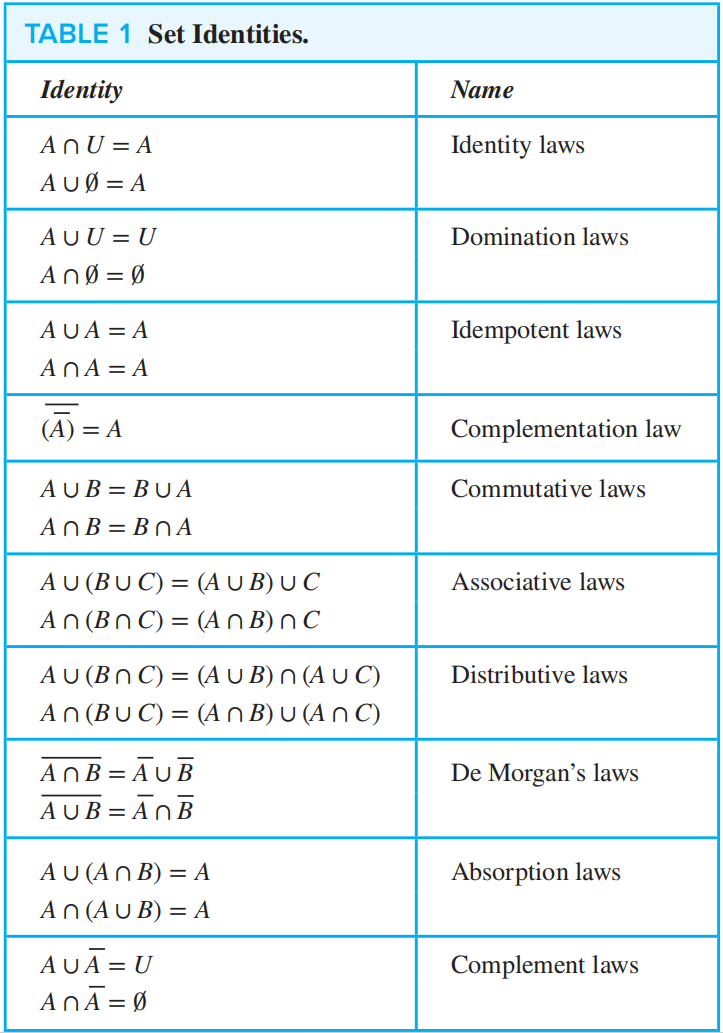
Set Identities⚓︎
🌟集合恒等式 (Set Identities)表
❗证明集合恒等式的方法:
- 子集法:证明两个集合互为对方的子集
- 成员表:类似真值表,用“1”表示元素在该集合内
, “0”表示不在集合内 - 运用已知恒等式:上表的公式
Generalized Unions and Intersections⚓︎
对于多个集合,我们对它们的并集和交集有如下定义:
- \(\bigcup\limits ^n _{i = 1} A_i= A_1 \cup A_2 \cup \dots \cup A_n\)
- \(\bigcap\limits ^n _{i = 1} A_i= A_1 \cap A_2 \cap \dots \cap A_n\)
对于无限集合,则有如下定义:
- \(\bigcup\limits ^{\infty} _{i = 1} A_i= A_1 \cup A_2 \cup \dots \cup A_n \cup \dots\)
- \(\bigcap\limits ^{\infty} _{i = 1} A_i= A_1 \cap A_2 \cap \dots \cap A_n \cap \dots\)
更一般地,如果 \(I\) 是个集合,则:
- \(\bigcup_{i \in I}A_i = \{x | \exists i \in I(x \in A_i)\}\)
- \(\bigcap_{i \in I}A_i = \{x | \forall i \in I(x \in A_i)\}\)
Computer Representations of Sets⚓︎
利用计算机表示集合的方法:
- 为全集 \(U\) 中的元素确定一个 ( 任意的 ) 顺序 ( 因为集合不规定顺序 ),比如 \(a_1, a_2, \dots, a_n\)
- 使用长度为 \(n\) 的位串表示 \(U\) 的子集 \(A\),如果 \(a_i \in A\),则 \(a_i = 1\),否则 \(a_i = 0\)
使用位串表示集合运算:
- 交集:AND
- 并集:OR
- 补集:按位取反
- 差集:利用 \(A - B = A \cap \overline{B}\),再利用上面交集和补集的方法
Multisets⚓︎
Multisets( 多重集 ):一个无序的元素集,元素可出现一次或多次,记为 \(\{m_1 \cdot a_1, m_2 \cdot a_2, \dots, m_r \cdot a_r\}\),其中 \(a_i\) 为元素,\(m_i\) 为其对应元素出现的次数
多重集的基数= \(\sum\limits_{i = 1}^r m_i\)
考虑两个多重集 \(P\) 和 \(Q\)
- 并集:保留元素出现个数最多的那项
- 交集:保留元素出现个数最少的那项
- 差集:\(m_i\) 为元素出现个数之差(注意顺序:\(P - Q\)
) ,如果结果小于 0,则取 0 - 和:\(m_i\) 为元素出现个数之和,记作 \(P + Q\)
Supplements(from Exercises)⚓︎
- \(A \subseteq B \Leftrightarrow \overline{B} \subseteq \overline{A}\)
- \((A - B) \cap (B - C) \cap (C - A) = \emptyset\)
- \(\overline{(A \cup B)} \cap \overline{(B \cup C)} \cap \overline{(A \cup C)} = \overline{A} \cap \overline{B} \cap \overline{C}\)
- \(A \times (B \cup C) = (A \times B) \cup (A \times C)\) \(A \times (B \cap C) = (A \times B) \cap (A \times C)\) \(A \times (B - C) = (A \times B) - (A \times C)\) \(\overline{A} \times \overline{(B \cup C)} = \overline{A \times (B \cup C)}\)
-
Jaccard similarity:\(J(A, B) = \dfrac{|A \cap B|}{|A \cup B|}\),\(J(\emptyset, \emptyset) = 1\)
Jaccard distance:\(d_J(A, B) = 1 - J(A, B)\)
有以下性质:
- \(J(A, A) = 1, d_J(A, A) = 0\)
- \(J(A, B) = J(B, A), d_J(A, B) = d_J(B, A)\)
- \(J(A, B) = 0, d_J(A, B) = 0\),当且仅当 \(A = B\)
- \(0 \le J(A, B) \le 1, 0 \le d_J(A, B) \le 1\)
- 三角不等式 (triangle inequality):\(d_J(A, C) \le d_J(A, B) + d_J(B, C)\)
-
模糊集 (fuzzy sets):全集 \(U\) 中的每个元素都有一个成员值 (degree of membership),范围为 \([0, 1]\),例如 \(F = \{0.6 \text{ Alice}, 0.9 \text{ Brian}, 0.1 \text{ Oscar}\}\)
- 补集:\(\overline{F}\) 的成员值 = 1 - \(F\) 的成员值
- 并集:两个模糊集中最大的成员值
- 交集:两个模糊集中最小的成员值
Functions⚓︎
Definition⚓︎
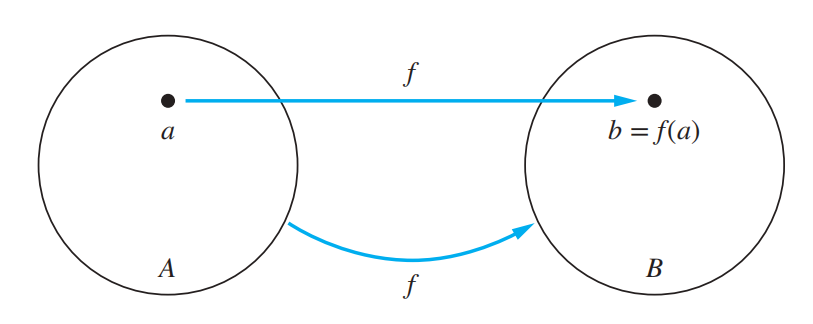
函数 (funtions, 又叫作 mappings/transformations):对于两个非空集合 \(A, B\),\(A\) 中的元素有且仅有一个对应于 \(B\) 上的元素。记作:\(f(a) = b\) 或 \(f: A \rightarrow B\),可用下面的逻辑语言表示:
表示方法:清晰的赋值语句、公式、计算机程序。
函数其实是 \(A\) 到 \(B\) 之间的关系 (relation),也就是笛卡尔积\(A \times B\) 的一个子集,因此 \(f(a) = b\) 也可记作 \((a, b)\)
- 域 (domain):\(A\)
- 伴域 (codomain):\(B\)
- 如果 \(f(a) = b\),则 \(b\) 是 \(a\) 的象 (image),而 \(a\) 是 \(b\) 的原象 (preimage)
- \(f\) 的范围 (range),是指对于集合 \(A\) 中所有元素的象,记作 \(f(A)\)
- 集合 \(A\) 的子集 \(S\) 的象,记作 \(f(S) = \{f(s) | s \in S\}\),注意 \(f(S)\) 代表的是一个集合
- 集合 \(B\) 的子集 \(S\) 的逆象 (inverse image),是集合 \(A\) 的一个子集,记为 \(f^{-1}(S) = \{a \in A | f(a) \in S\}\)。 它们的性质见最后的补充部分
如果两个函数有相同的域,相同的伴域,和相同的映射关系,则称这两个函数相等
函数的加法和乘法:
One-to-one and Onto Functions⚓︎
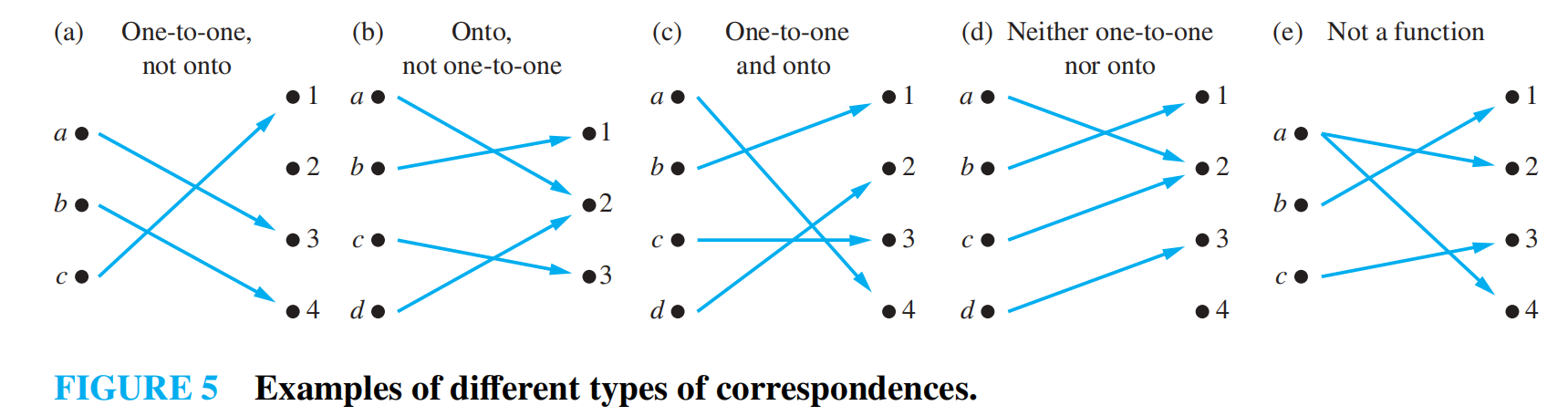
- 单射 (injection, one-to-one):当 \(f(a) = f(b)\),得到 \(a = b\)
逻辑语言:
注
若 \(x, y\) 在 \(f\) 的域内,且 \(x < y\),则:
- 单调递增:\(f(x) \le f(y)\),即 \(\forall x \forall y(x < y \rightarrow f(x) \le f(y))\)
- 单调递减:\(f(x) \ge f(y)\),即 \(\forall x \forall y(x < y \rightarrow f(x) \ge f(y))\)
- 严格单调递增:\(f(x) < f(y)\),即 \(\forall x \forall y(x < y \rightarrow f(x) < f(y))\)
- 严格单调递减:\(f(y) > f(y)\),即 \(\forall x \forall y(x < y \rightarrow f(x) > f(y))\)
其中只有严格单增 / 减函数满足单射
- 满射 (surjection, onto):对于每个 \(b \in B\),都有 \(a \in A\),使得 \(f(a) = b\)
逻辑语言:\(\forall y \exists x (f(x) = y)\)
- 双射 (bijection, one-to-one correspondence):既是单射也是满射的函数
对于 \(A \rightarrow B\) 的一个双射,\(|A| = |B|\),即两个集合基数相同
判断单射或满射的方法:
恒等函数 (identity function):\(\iota_A: A \rightarrow A\),即 \(\iota_A(x) = x\),它是一个双射的函数
Inverse Functions and Compositions of Functions⚓︎
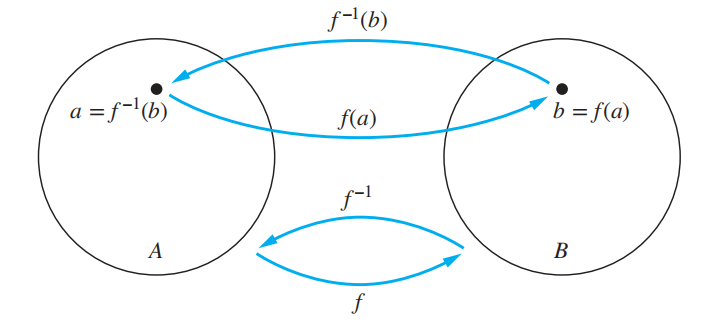
反函数 (inverse function):对于一个双射函数 \(f: A \rightarrow B\),它的反函数为 \(f^{-1}: B \rightarrow A\),即当 \(f(a) = b\) 时,\(f^{-1}(b) = a\)
记住:只有双射函数有反函数
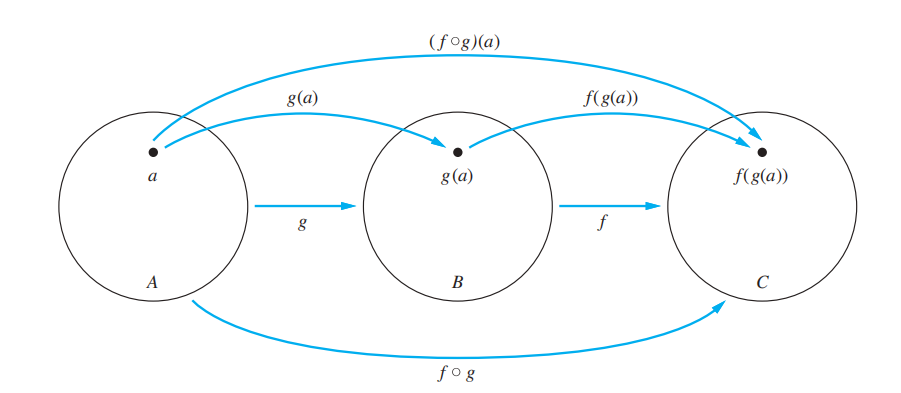
复合函数 (composition of the functions):\((f \circ g)(a) = f(g(a))\)
注:
- \(f \circ g\) 的域为 \(g\) 的域
- \(f \circ g\) 的范围为 \(g\) 关于 \(f\) 的范围
- 只有当 \(g\) 的范围为 \(f\) 的域的子集时,\(f \circ g\) 才有定义
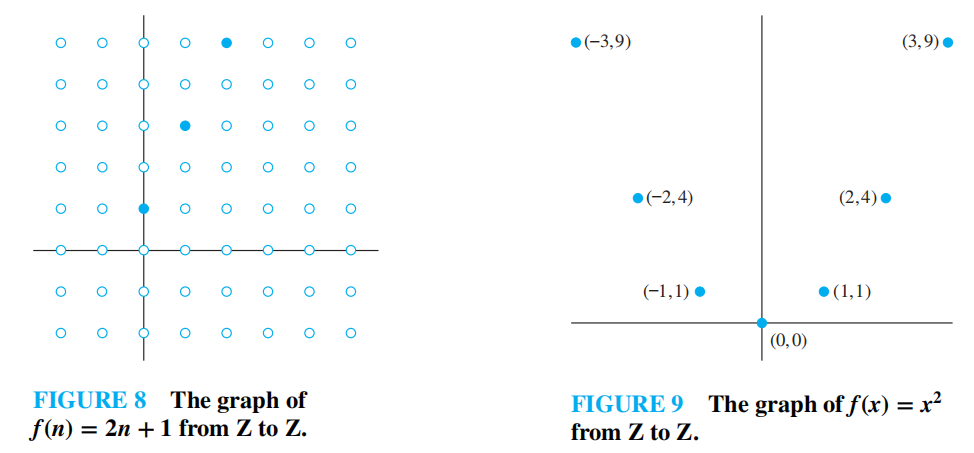
The Graph of Functions⚓︎
函数 \(f\) 的图象 (graph) 是一个有序对的集合 \(\{(a, b) | a \in A \text{ and } f(a) = b\}\)
🌰:
Some Important Functions⚓︎
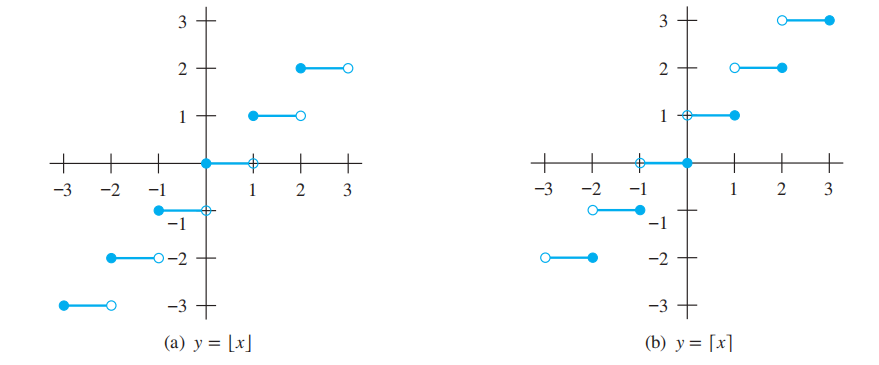
- 底函数 (floor function):\(\lfloor x \rfloor\),取不大于 \(x\) 的最大整数
- 顶函数 (ceiling function):\(\lceil x \rceil\),取不小于 \(x\) 的最小整数
图象:
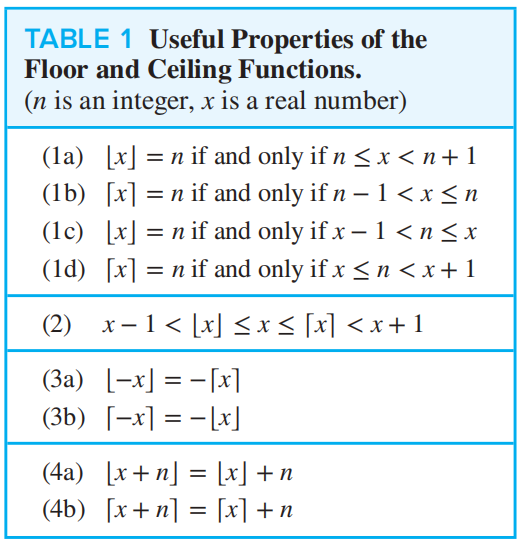
❗重要性质:
🌰:
Partial Function⚓︎
Supplements(from Exercises)⚓︎
- \(f(S \cup T) = f(S) \cup f(T) \quad \quad f(S \cap T) \subseteq f(S) \cap f(T)\)
- \(f^{-1}(S \cup T) = f^{-1}(S) \cup f^{-1}(T) \quad \quad f^{-1}(S \cap T) = f^{-1}(S) \cap f^{-1}(T)\)
- \(f^{-1}(\overline{S}) = \overline{f^{-1}(S)}\)
- 特征函数 (Characteristic function):\(f_S: U \rightarrow \{0, 1\}\),当 \(x\) 在 \(S\) 中时,\(f_S(x) = 1\),否则 \(f_S(x) = 0\)
- 对于函数 \(f: A \rightarrow B\),\(|A| = |B|\),\(f\) 为单射函数的充要条件是 \(f\) 为满射函数
- 集合 \(S\) 是无限的充要条件是 \(S\) 的子集 \(A\) 与 \(S\) 是双射关系
Sequences and Summations⚓︎
Sequences⚓︎
序列 (sequences):一个从整数集合(通常是 \(\{0, 1, 2, \dots\}\) 或 \(\{1, 2, 3,\dots\}\))映射到某个集合 \(S\) 的函数,一般用 \(\{a_n\}\) 表示一个序列(不要和集合的记号弄混)
一些特殊序列:
- 等比数列 (geometric progression):\(a, ar, ar^2, \dots, ar^n, \dots\) 其中\(a\)被称为首项,\(r\) 被称为公比
- 等差数列 (arithmetric progression):\(a, a + d, a + 2d, \dots, a + nd, \dots\) 其中\(a\)被称为首项,\(d\) 被称为公差
- 字符串 (string):包含字符的有限序列,可用 \(a_1, a_2, \dots, a_n\) 标记
- 应用:位串
- 长度 (length):字符串包含项的个数
- 空串 (empty string):长度为 0,记作 \(\lambda\)
Recurrence Relations⚓︎
递推关系 (recurrence relations):一个用于表示 \(a_n\) 的表达式,由它前面的项 \(a_0, a_1, \dots, a_{n - 1}\) 构成
如果一个序列能够满足递推关系,那这个序列被称为solution( 通解?)
因为序列的首项前面没有东西,因此需要起始条件 (initial conditions)才能使递推关系生效
斐波那契数列 (Fibonacci sequence):起始条件为 \(f_0 = 0, f_1 = 1\),且满足递推关系 \(f_n = f_{n - 1} + f_{n - 2}, n = 2, 3, 4, \dots\)
闭合公式 (closed formula):一个能够解出递推关系及其起始条件的公式
求解方法:
注:更多的技巧见 Chap 8,现在仅介绍简单的方法
迭代 (iteration):
- 前代 (forward substitution):从首项开始代入递推关系,直至 \(a_n\) 项
- 回代 (backward substitution):从 \(a_n\) 项开始往回代,直到首项 \(a_1\)
我们使用迭代大致猜出这个序列的通解,还需要通过数学归纳法 (mathematical induction)检验,这将在 Chap 5 讲解
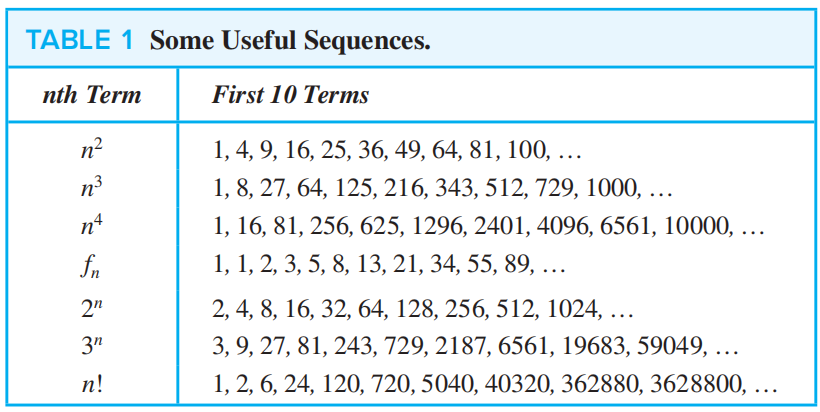
Special Integer Sequences⚓︎
有时,我们只知道一个序列的前面几项,但是通过一些技巧,我们也能判断出该序列的 solution:
- 该序列是否出现过相同的值,如果有的话,出现了多少次?
- 该序列的项是否通过对前面某些项的相加得到?
- 该序列的项是否通过对前面某些项的相乘得到?
- 该序列的项是否通过对前面某些项的某种组合?
- 该序列是否有周期性
- 该序列是否与我们所熟知的一些序列(见下表)有关
Summations⚓︎
这里没什么东西好说,可能有点用的就是下面这张表👇
Supplements(from Exercises)⚓︎
- telescoping( 套管式?):\(\sum\limits_{j = 1}^n(a_j - a_{j - 1}) = a_n - a_0\)
- 累积:\(\prod\limits_{j = m}^n a_j\)
Cardinality of Sets⚓︎
The Cardinality of a Finite Set⚓︎
拓展:
一共有 \(C^1_n + C^2_n + \dots + C^n_n = 2^n - 1\) 项
注:Chap 8 还会详细介绍
Extend to Infinite Set⚓︎
当且仅当 \(A\) 与 \(B\) 存在双射的关系,集合 \(A\) 与 \(B\) 基数相等(这样就不用具体比较集合的大小)
- 如果集合 \(A \rightarrow B\) 存在单射的关系,则 \(|A| \le |B|\)
- 如果 \(|A| \le |B|\) 且 \(|A| \ne |B|\),则 \(|A| < |B|\)
Countable Sets⚓︎
如果一个集合:
- 是有限集
- 或者,与正整数集\(\mathbb{Z}^+\) 有相同的基数的无限集
则这个集合是可数的 (countable),否则是不可数的 (uncountable)
可数集合的基数 \(|S|\) 用 \(\aleph_0\) 表示
⭐判断方法:当能够列出以序列 (sequence) 元素为集合的所有元素(即双射关系 \(f: Z^+ \rightarrow {a_n}\),有 \(a_1 = f(1), a_2 = f(2), \dots, a_n = f(n), \dots\)
例题
Uncountable Sets⚓︎
定理 1:如果集合 \(A\) 和 \(B\) 是可数的,则 \(A \cup B\) 也可数
拓展
- 有限个可数集合的交集也是可数的
- 可数数字个可数集合的交集也是可数的 ( 见 Exercise 27)
定理 2(SCHRODER-BERNSTEIN THEOREM):如果 \(|A| \le |B|\) 且 \(|B| \le |A|\),则 \(|A| = |B|\)。也就是说,如果 \(A \rightarrow B\) 是单射的,\(B \rightarrow A\) 也是单射的,则 \(A\) 与 \(B\) 有双射的
- 反过来也成立
- 看似简单的定理,证明起来一点也不简单,但结论挺好记的😁
❗其他定理 / 结论:
- \((0, 1)\) 之间的实数不可数
- 所有实数都不可数
来自习题的补充:
- 不存在这样的无限集,它的基数小于可数集合的基数
- \(A, B\) 为两个集合,且 \(A \subset B \rightarrow |A| \le |B|\)
- \(A, B\) 为两个集合,\(A\) 不可数且 \(A \subseteq B \rightarrow B\) 不可数
- 可数集合的子集也是可数的
- \(|A| = |B| \rightarrow |P(A)| = |P(B)|\)
- \((|A| = |B|) \wedge (|C| = |D|) \rightarrow |A \times C| = |B \times D|\)
- \((|A| = |B|) \wedge (|B| = |C|) \rightarrow |A| = |C|\)
- \((|A| \le |B|) \wedge (|B| \le |C|) \rightarrow |A| \le |C|\)
- \(A\) 是可数集合,且存在满射 \(f: A \rightarrow B\),则 \(B\) 也是可数集合
- 如果 \(A\) 是无限集合,则存在一个可数的无限子集
- 不存在这样的无限集合 \(A\),使得 \(|A| < |\mathbb{Z}^+| = \aleph_0\)
-
一个包含元素为从正整数映射到 \(\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\) 的函数的集合是不可数的
-
( 来自历年卷 ) 存在可数无限集 \(A\),使得存在一个双射:\(A \rightarrow A \times A\)
例子:康托配对函数,虽然它是一个 \(\mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}\) 的双射函数,但双射函数的反函数也是双射的,这就符合上面的结论了
Applications⚓︎
-
如果一个计算机程序能够找到这个函数的值,则称该函数为可计算的 (computable),否则被称为不可计算 (uncomputable)
-
幂集的基数总是大于它对应的一般集合的基数
- \(|P(Z^+)| = |R| = c\)
- 连续统假设 (continuum hypothesis):不存在这样的基数 \(a\),使得 \(\aleph_0 < a < \aleph_1\)
Matrices⚓︎
虽然划掉了(考试不考
) ,但这里还是稍微提一下基本概念
矩阵 (matrix):\(\mathbf{A} = \begin{bmatrix}a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix}\),可简写为 \(\mathbf{A} = [a_{ij}]\)
相等:当且仅当两个矩阵的规模相同(行、列数相同)且每个位置的元素都相等时,两个矩阵相等
加法:当矩阵 \(\mathbf{A}, \mathbf{B}\) 均为 \(m \times n\) 的矩阵时,\(\mathbf{A} + \mathbf{B} = [a_{ij} + b_{ij}]\)
矩阵加法满足交换律、结合律
乘法:当矩阵 \(\mathbf{A}\) 的规模为 \(m \times k\),矩阵 \(\mathbf{B}\) 的规模为 \(k \times n\) 时,\(\mathbf{AB} = [c_{ij}]\),其中 \(c_{ij} = \sum\limits_{t = 1}^ka_{it}b_{tj}\)
注意:矩阵乘法有结合律和分配律,但交换律不成立
单位矩阵 (identity matrix):\(\mathbf{I}_n = \begin{bmatrix}1 & 0 & \dots & 0 \\ 0 & 1 &\dots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \dots & 1\end{bmatrix} = [\delta_{ij}]\),其中 \(\delta_{ij}= \begin{cases}1 & \text{if } i = j, \\ 0 & \text{if } i \ne j.\end{cases}\)
性质:对于规模为 \(m \times n\) 的矩阵 \(\mathbf{A}\),\(\mathbf{AI}_n = \mathbf{I}_m\mathbf{A} = \mathbf{A}\)
幂:\(\mathbf{A}^0 = \mathbf{I}_n, \quad \quad \mathbf{A}^r = \underbrace{\mathbf{AAA} \dots \mathbf{A}}_{r \text{ times}}\)
转置 (transpose):规模为 \(m \times n\) 的矩阵 \(\mathbf{A} = [a_{ij}]\) 的转置矩阵为 \(\mathbf{A}^t = [b_{ij}]\),规模为 \(n \times m\),其中 \(b_{ij} = a_{ji}\)
性质
- \((\mathbf{A}^t)^t = \mathbf{A}\)
- \((\mathbf{A} + \mathbf{B})^t = \mathbf{A}^t + \mathbf{B}^t\)
- \((\mathbf{AB})^t = \mathbf{B}^t\mathbf{A}^t\)
对称矩阵 (symmetric matrix),对于方阵\(\mathbf{A}\),如果 \(\mathbf{A} = \mathbf{A}^t\),则 \(\mathbf{A}\) 为对称矩阵(\(\mathbf{A}\) 内的元素关于主对角线对称)
注
可以证明下列矩阵为对称矩阵——
- \(\mathbf{AA}^t\)
- \(\mathbf{A} + \mathbf{A}^t\)
零一矩阵 (zero-one matrix):元素仅为 0 或 1 的矩阵(与布尔运算紧密相关)
对于两个规模均为 \(m \times n\) 零一矩阵 \(\mathbf{A} = [a_{ij}], \mathbf{B} = [b_{ij}]\)
- 并 (join):\(\mathbf{A} \vee \mathbf{B}\),每个元素为 \(a_{ij} \vee b_{ij}\)
- 交 (meet):\(\mathbf{A} \wedge \mathbf{B}\),每个元素为 \(a_{ij} \wedge b_{ij}\)
性质
- \(\mathbf{A} \vee \mathbf{A} = \mathbf{A}\)
- \(\mathbf{A} \wedge \mathbf{A} = \mathbf{A}\)
- 相同运算符的情况下满足交换律和结合律
- 分配律:
\(\mathbf{A} \vee (\mathbf{B} \wedge \mathbf{C}) = (\mathbf{A} \vee \mathbf{B}) \wedge (\mathbf{A} \vee \mathbf{C}) \quad \quad \mathbf{A} \wedge (\mathbf{B} \vee \mathbf{C}) = (\mathbf{A} \wedge \mathbf{B}) \vee (\mathbf{A} \wedge \mathbf{C})\)
对于两个零一矩阵 \(\mathbf{A}\)(规模为 \(m \times k\))和 \(\mathbf{B}\)(规模为 \(k \times n\)
- 布尔积 (Boolean product):\(\mathbf{A} \odot \mathbf{B}\)(规模为 \(m \times n\)
) ,每个元素 \(c_{ij} = \bigvee\limits_{t = 1}^k (a_{it} \wedge b_{tj})\) - 布尔幂 (Boolean power):\(\mathbf{A}^{[r]} = \underbrace{\mathbf{A} \odot\mathbf{A} \odot\mathbf{A} \odot \dots \odot\mathbf{A}}_{r \text{ times}}\),规定 \(\mathbf{A}^{[0]} = \mathbf{I}_n\)
性质
- \(\mathbf{A} \odot \mathbf{I} = \mathbf{I} \odot \mathbf{A} = \mathbf{A}\)
- 结合律
Supplements(from Exercises)⚓︎
对角矩阵 (diagonal matrix):对于 \(n \times n\) 方阵 \(\mathbf{A} = [a_{ij}]\),如果当 \(i \ne j\) 时,\(a_{ij} = 0\) 成立,则 \(\mathbf{A}\) 为对称矩阵
逆矩阵 (inverse):如果 \(\mathbf{A}, \mathbf{B}\) 为 \(n \times n\) 的方阵,且 \(\mathbf{AB} = \mathbf{BA} = \mathbf{I}_n\),则称 \(\mathbf{B}\) 为 \(\mathbf{A}\) 的逆矩阵,记作 \(\mathbf{B} = \mathbf{A}^{-1}\) 性质: \((\mathbf{A}^n)^{-1} = (\mathbf{A}^{-1})^n\)
利用矩阵解线性方程组(略)
评论区