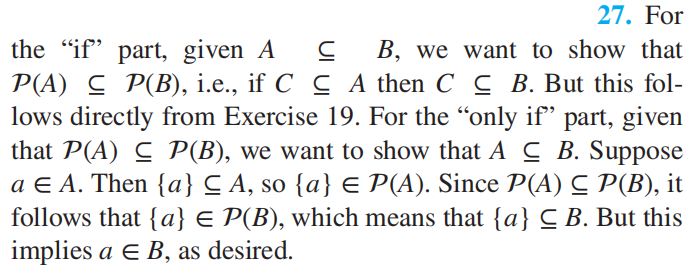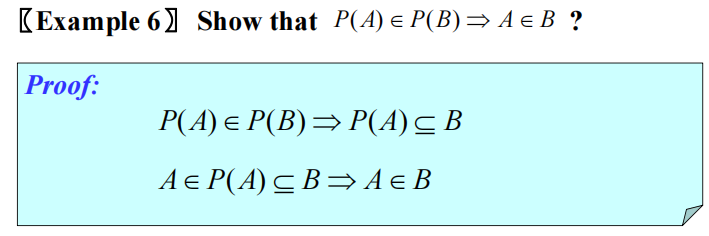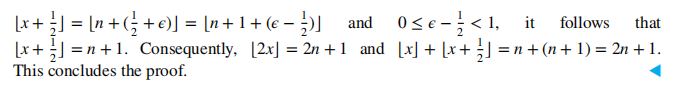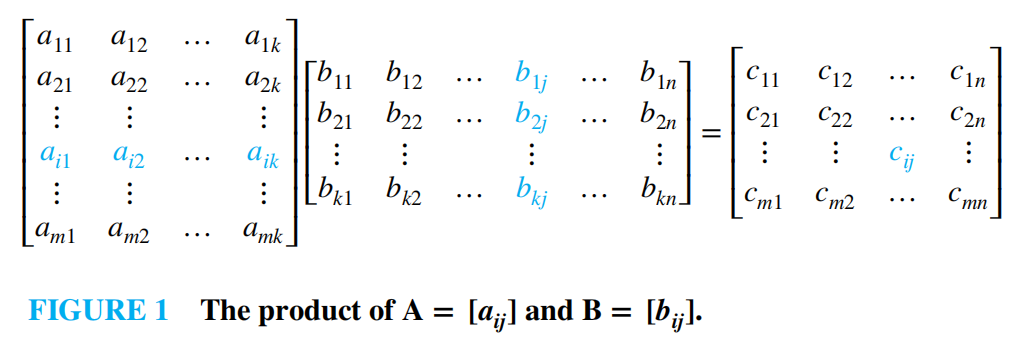Chap 2 Basic Structures: Sets, Functions, Sequences, Sums, and Matrices⚓︎

Sets⚓︎

Introduction⚓︎

集合 (set)：一组拥有不同对象（被称为元素 (element)）的无序集

• \(a \in A\)：\(a\) 是 \(A\) 中的一个元素
• \(a \notin A\)：\(a\) 不是 \(A\) 中的一个元素

The Description of Sets⚓︎

1. 枚举法 (roster method)：用花括号 { } 包含所有元素，比如 \(S = \{a, b, c, d\}\)

如果元素个数太多，可用省略号 (ellipses)(...) 表示

2. set builder：\(\{x | x \text{ has property }P\}\)，对于集合中的所有 \(x\) 元素，都具有 \(P\) 性质

数学中常用的一些集合：

• 自然数集 \(\mathbb{N} = \{0, 1, 2, 3, \dots \}\)
• 整数集 \(\mathbb{Z} = \{\dots, -2, -1, 0, 1, 2 \dots \}\)
• 正整数集 \(\mathbb{Z^+} = \{1, 2, 3, \dots\}\)
• 有理数集 \(\mathbb{Q} = \{\dfrac{p}{q} | p \in \mathbb{Z}, q \in \mathbb{Z}, \text{and } q \ne 0\}\)
• 实数集 \(\mathbb{R}\)， 正实数集 \(\mathbb{R^+}\)
• 复数集 \(\mathbb{C}\)

3. 区间 (intervals)：

• 闭区间 (closed interval)：\([a, b] = \{ x | a \le x \le b \}\)
• 开区间 (open interval)：\((a, b) = \{ x | a < x < b\}\)
• 还有：\([a, b) = \{x | a \le x < b\} \quad (a, b] = \{x | a < x \le b\}\)

注：在 CS 中，数据类型 (datatype) 也是一种集合，同时也包含了一些运算的集合

相等：\(A = B\)，当且仅当 \(\forall x(x \in A \leftrightarrow x \in B)\)，或者 \((A \subseteq B) \wedge (B \subseteq A)\)

空集 (empty Set/ null Set)：没有元素的集合，用 "\(\emptyset\)" 表示

单元素集合 (singleton set)：只有一个元素的集合

注意：\(\emptyset \ne \{\emptyset\}\)

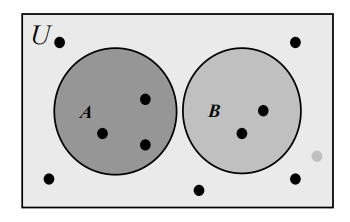
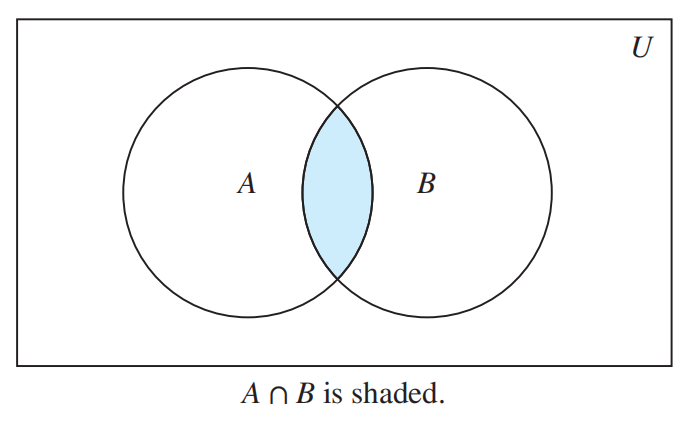
Veen Diagram⚓︎

细节：

• 用矩形表示全集 (universal Set)\(U\)
• 矩形中的每个圆圈表示集合
• 用点表示元素

Subsets⚓︎

\(A\) 是 \(B\) 的子集 (subset) = \(B\) 是 \(A\) 的超集 (superset)，即 \(A\) 中的每个元素都是 \(B\) 的元素

记号：\(A \subseteq B\) 或 \(B \supseteq A\)，等价于 \(\forall x(x \in A \rightarrow x \in B)\)

• 如何说明 \(A \subseteq B\)：说明每个属于 A 的元素也属于 B
• 如何说明 \(A \nsubseteq B\)：找到一个元素 \(x\)，使得 \(x \in A\) 但 \(x \notin B\)

定理：对于每个集合 \(S\)，\(\text{(i)} \emptyset \subseteq S \quad \text{(ii)} S \subseteq S\)

真子集 (proper subset)：\(A\) 是 \(B\) 的子集，但 \(A \ne B\)，记作 \(A \subset B\)。

也就是说，\(\forall x(x \in A \rightarrow x \in B) \wedge \exists x(x \in B \wedge x \notin A)\)

The Size of a Set⚓︎

如果 \(S\) 有 \(n\) 个不同的元素，称 \(S\) 为有限集 (finite Set)，且 \(n\) 是 \(S\) 的基数 (cardinality)，记作 \(|S|\)；否则认为该集合是无限的 (infinite)

基数的概念在后面会详细介绍

Power Sets⚓︎

幂集合 (power Sets)：包含集合 \(S\) 的所有子集的集合，记作 \(P(S) = \{x | x \subseteq S\}\) 如果集合有\(n\)个元素，则它对应的幂集合有\(2^n\)个元素

性质：

• \(P(A) \in P(B) \rightarrow A \in B\)
• \(P(A) \subseteq P(B) \leftrightarrow A \subseteq B\)

证明

Cartesian Products⚓︎

有序 n 元组 (The ordered n-tuple)\((a_1, a_2, \dots, a_n)\) $$ (a_1, a_2, \dots, a_n) = (b_1, b_2, \dots, b_n) \Leftrightarrow a_i = b_i(i = 1, 2, \dots, n) $$

有序对 (Ordered pairs)：\(n = 2\) 的有序 n 元组

注意：\((a, b) \ne (b, a)\)，除非 \(a = b\)

笛卡尔积 (Cartesian Products)：\(A \times B = \{(a, b) | a \in A \wedge b \in B\}\)

对于多个集合的笛卡尔积：

当 \(A_1 = A_2 = \dots = A_n = A\) 时，

性质：

• 如果 \(|A| = m, |B| = n\)，那么 \(|A \times B| = |B \times A| = mn\)
• \(A \times B \ne B \times A\)，除非 \((A = \emptyset) \vee (B = \emptyset) \vee (A = B)\)
• \((A \times B) \times C \ne A \times B \times C\)
• \(A \times \emptyset = \emptyset \times A = \emptyset\)
• \((x, y) \in A \times B \Rightarrow x \in A \wedge y \in B \quad \quad (x, y) \notin A \times B \Rightarrow x \notin A \vee y \notin B\)

Using Set Notation with Quantifiers⚓︎

Truth Sets and Quantifiers⚓︎

真值集 (truth sets)\(P\) 是指对于某个域 \(D\) 的所有 \(x\)，都有 \(P(x)\) 为真，即 \(\{x \in D|P(x)\}\)

• 当且仅当它的真值集 \(P\) 为集合 \(U\) 时，\(\forall xP(x)\) 在全集域 \(U\) 为真
• 当且仅当它的真值集 \(P\) 非空时，\(\exists xP(x)\) 在全集域 \(U\) 为真

Supplements(from Exercises)⚓︎

罗素悖论 (Russell's paradox)：\(S = \{ x | x \notin x\}\)

经典例子：理发师悖论

Set Operations⚓︎

Set Operations⚓︎

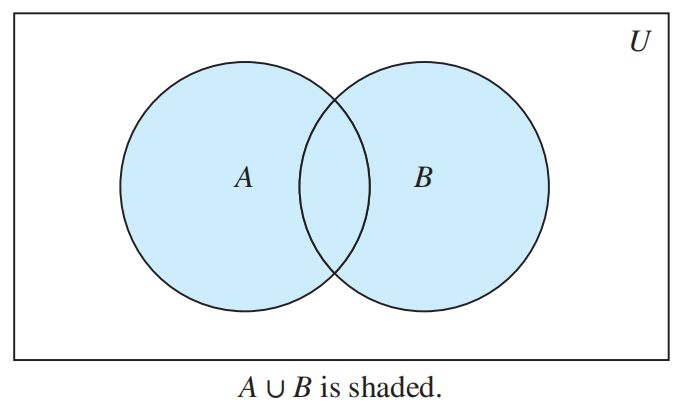
• 并集 (union)：\(A \cup B = \{x|x \in A \vee x \in B\}\)

• 交集 (intersection)：\(A \cap B = \{x|x \in A \wedge x \in B\}\)。如果 \(A \cap B = \emptyset\)，被称为不相交 (disjoint) 集。

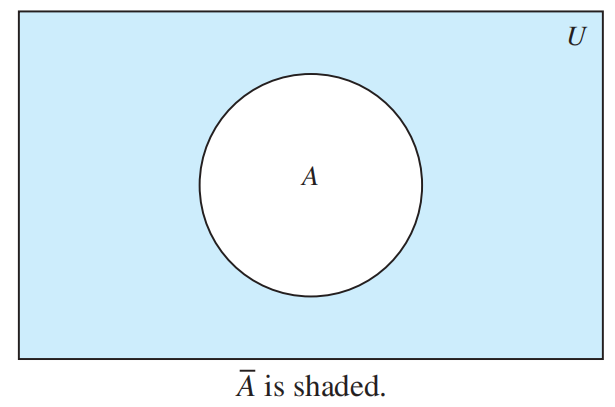
• 补集 (complement)：在全集 \(U\) 中，集合 \(A\) 的补集为 \(\overline{A}\)，它是关于 \(U\) 的 \(A\) 的补，即 \(U - A\). \(\overline{A} = \{x \in U | x \notin A\}\)

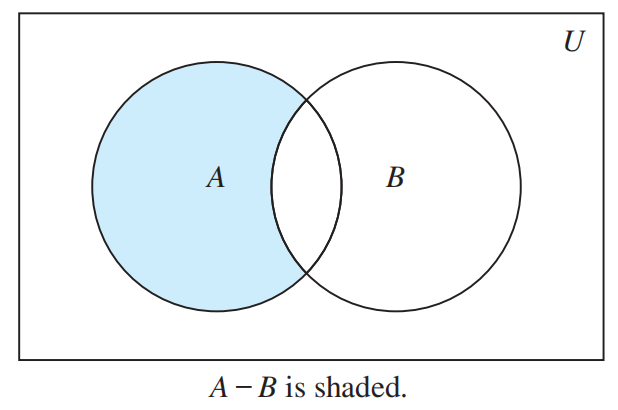
• 差集 (difference)：\(A - B = \{x | x \in A \wedge x \notin B\} = A \cap \overline{B}\)

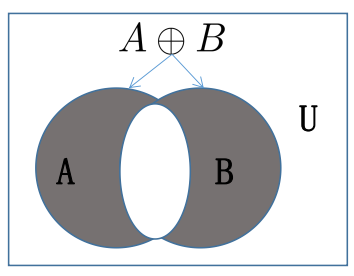
• （补充）对称差集 (symmetric difference)：\(A \oplus B = (A \cup B) - (A \cap B) = (A - B) \cup (B - A)\)

注：本质上就是异或 (xor)

More on Set Cardinality⚓︎

⭐容斥原理 (The Principle of Inclusion-Exclusion)：

注：Chap 8 会详细介绍

Set Identities⚓︎

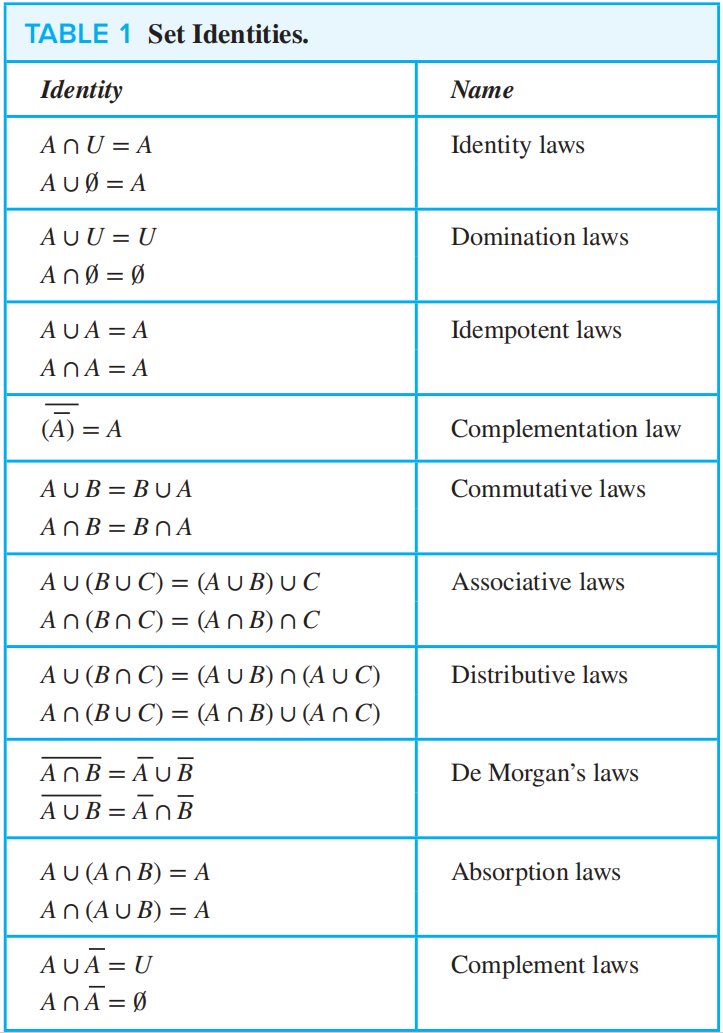
🌟集合恒等式 (Set Identities)表

❗证明集合恒等式的方法：

1. 子集法：证明两个集合互为对方的子集
2. 成员表：类似真值表，用“1”表示元素在该集合内，“0”表示不在集合内
3. 运用已知恒等式：上表的公式

Generalized Unions and Intersections⚓︎

对于多个集合，我们对它们的并集和交集有如下定义：

• \(\bigcup\limits ^n _{i = 1} A_i= A_1 \cup A_2 \cup \dots \cup A_n\)
• \(\bigcap\limits ^n _{i = 1} A_i= A_1 \cap A_2 \cap \dots \cap A_n\)

对于无限集合，则有如下定义：

• \(\bigcup\limits ^{\infty} _{i = 1} A_i= A_1 \cup A_2 \cup \dots \cup A_n \cup \dots\)
• \(\bigcap\limits ^{\infty} _{i = 1} A_i= A_1 \cap A_2 \cap \dots \cap A_n \cap \dots\)

更一般地，如果 \(I\) 是个集合，则：

• \(\bigcup_{i \in I}A_i = \{x | \exists i \in I(x \in A_i)\}\)
• \(\bigcap_{i \in I}A_i = \{x | \forall i \in I(x \in A_i)\}\)

Computer Representations of Sets⚓︎

利用计算机表示集合的方法：

• 为全集 \(U\) 中的元素确定一个 ( 任意的 ) 顺序 ( 因为集合不规定顺序 )，比如 \(a_1, a_2, \dots, a_n\)
• 使用长度为 \(n\) 的位串表示 \(U\) 的子集 \(A\)，如果 \(a_i \in A\)，则 \(a_i = 1\)，否则 \(a_i = 0\)

使用位串表示集合运算：

• 交集：AND
• 并集：OR
• 补集：按位取反
• 差集：利用 \(A - B = A \cap \overline{B}\)，再利用上面交集和补集的方法

Multisets⚓︎

Multisets( 多重集 )：一个无序的元素集，元素可出现一次或多次，记为 \(\{m_1 \cdot a_1, m_2 \cdot a_2, \dots, m_r \cdot a_r\}\)，其中 \(a_i\) 为元素，\(m_i\) 为其对应元素出现的次数

多重集的基数= \(\sum\limits_{i = 1}^r m_i\)

考虑两个多重集 \(P\) 和 \(Q\)

• 并集：保留元素出现个数最多的那项
• 交集：保留元素出现个数最少的那项
• 差集：\(m_i\) 为元素出现个数之差（注意顺序：\(P - Q\)），如果结果小于 0，则取 0
• 和：\(m_i\) 为元素出现个数之和，记作 \(P + Q\)

Supplements(from Exercises)⚓︎

• \(A \subseteq B \Leftrightarrow \overline{B} \subseteq \overline{A}\)
• \((A - B) \cap (B - C) \cap (C - A) = \emptyset\)
• \(\overline{(A \cup B)} \cap \overline{(B \cup C)} \cap \overline{(A \cup C)} = \overline{A} \cap \overline{B} \cap \overline{C}\)
• \(A \times (B \cup C) = (A \times B) \cup (A \times C)\) \(A \times (B \cap C) = (A \times B) \cap (A \times C)\) \(A \times (B - C) = (A \times B) - (A \times C)\) \(\overline{A} \times \overline{(B \cup C)} = \overline{A \times (B \cup C)}\)

• Jaccard similarity：\(J(A, B) = \dfrac{|A \cap B|}{|A \cup B|}\)，\(J(\emptyset, \emptyset) = 1\)

  Jaccard distance：\(d_J(A, B) = 1 - J(A, B)\)

  有以下性质：

  • \(J(A, A) = 1, d_J(A, A) = 0\)
  • \(J(A, B) = J(B, A), d_J(A, B) = d_J(B, A)\)
  • \(J(A, B) = 0, d_J(A, B) = 0\)，当且仅当 \(A = B\)
  • \(0 \le J(A, B) \le 1, 0 \le d_J(A, B) \le 1\)
  • 三角不等式 (triangle inequality)：\(d_J(A, C) \le d_J(A, B) + d_J(B, C)\)

• 模糊集 (fuzzy sets)：全集 \(U\) 中的每个元素都有一个成员值 (degree of membership)，范围为 \([0, 1]\)，例如 \(F = \{0.6 \text{ Alice}, 0.9 \text{ Brian}, 0.1 \text{ Oscar}\}\)

  • 补集：\(\overline{F}\) 的成员值 = 1 - \(F\) 的成员值
  • 并集：两个模糊集中最大的成员值
  • 交集：两个模糊集中最小的成员值

Functions⚓︎

Definition⚓︎

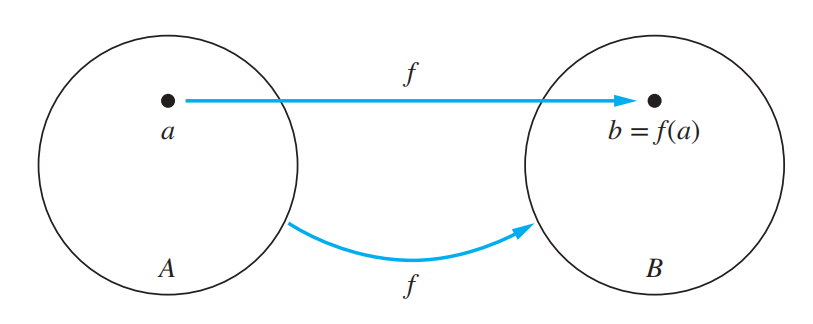
函数 (funtions, 又叫作 mappings/transformations)：对于两个非空集合 \(A, B\)，\(A\) 中的元素有且仅有一个对应于 \(B\) 上的元素。记作：\(f(a) = b\) 或 \(f: A \rightarrow B\)，可用下面的逻辑语言表示：

表示方法：清晰的赋值语句、公式、计算机程序。

函数其实是 \(A\) 到 \(B\) 之间的关系 (relation)，也就是笛卡尔积\(A \times B\) 的一个子集，因此 \(f(a) = b\) 也可记作 \((a, b)\)

• 域 (domain)：\(A\)
• 伴域 (codomain)：\(B\)
• 如果 \(f(a) = b\)，则 \(b\) 是 \(a\) 的象 (image)，而 \(a\) 是 \(b\) 的原象 (preimage)
• \(f\) 的范围 (range)，是指对于集合 \(A\) 中所有元素的象，记作 \(f(A)\)
  • 集合 \(A\) 的子集 \(S\) 的象，记作 \(f(S) = \{f(s) | s \in S\}\)，注意 \(f(S)\) 代表的是一个集合
  • 集合 \(B\) 的子集 \(S\) 的逆象 (inverse image)，是集合 \(A\) 的一个子集，记为 \(f^{-1}(S) = \{a \in A | f(a) \in S\}\)。 它们的性质见最后的补充部分

如果两个函数有相同的域，相同的伴域，和相同的映射关系，则称这两个函数相等

函数的加法和乘法：

One-to-one and Onto Functions⚓︎

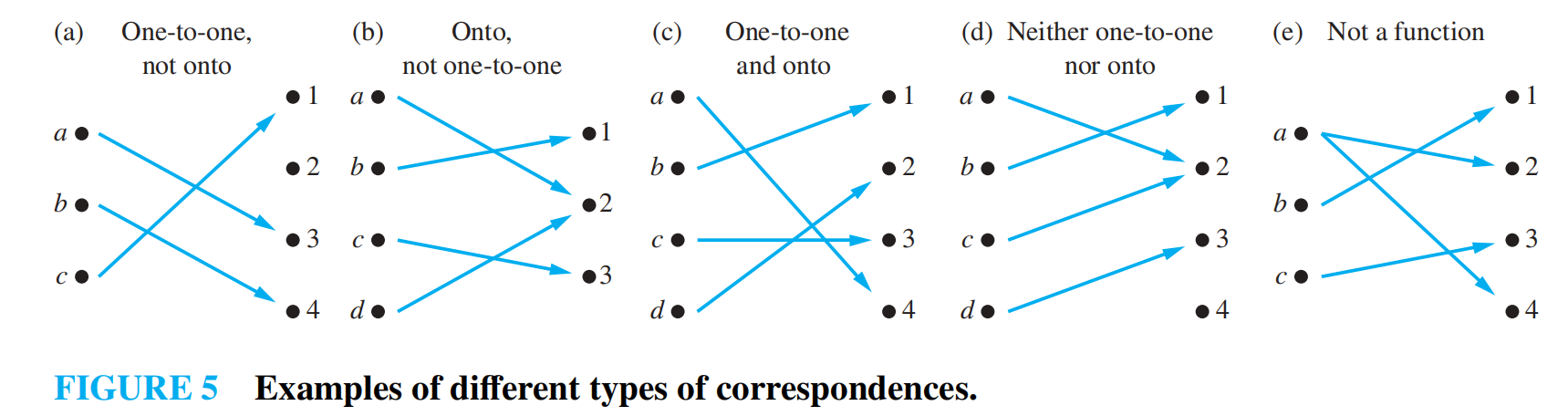
• 单射 (injection, one-to-one)：当 \(f(a) = f(b)\)，得到 \(a = b\)

逻辑语言：

• 满射 (surjection, onto)：对于每个 \(b \in B\)，都有 \(a \in A\)，使得 \(f(a) = b\)

逻辑语言：\(\forall y \exists x (f(x) = y)\)

• 双射 (bijection, one-to-one correspondence)：既是单射也是满射的函数

对于 \(A \rightarrow B\) 的一个双射，\(|A| = |B|\)，即两个集合基数相同

判断单射或满射的方法：

恒等函数 (identity function)：\(\iota_A: A \rightarrow A\)，即 \(\iota_A(x) = x\)，它是一个双射的函数

Inverse Functions and Compositions of Functions⚓︎

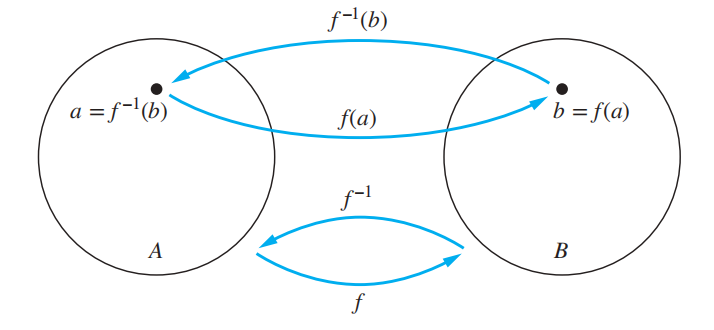
反函数 (inverse function)：对于一个双射函数 \(f: A \rightarrow B\)，它的反函数为 \(f^{-1}: B \rightarrow A\)，即当 \(f(a) = b\) 时，\(f^{-1}(b) = a\)

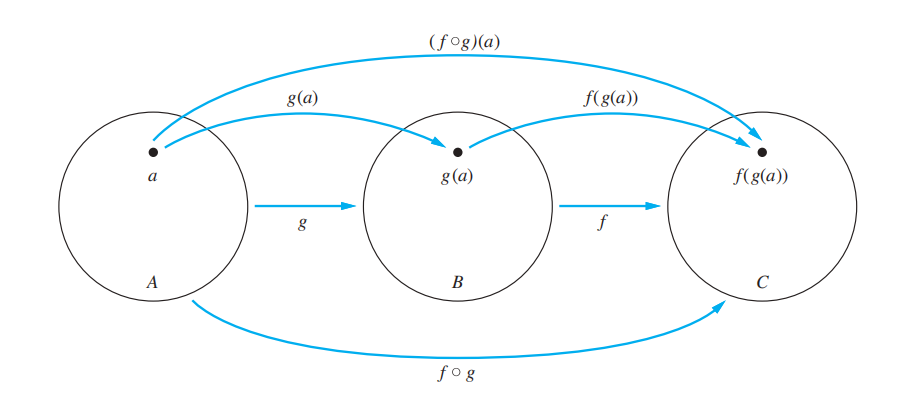
复合函数 (composition of the functions)：\((f \circ g)(a) = f(g(a))\)

The Graph of Functions⚓︎

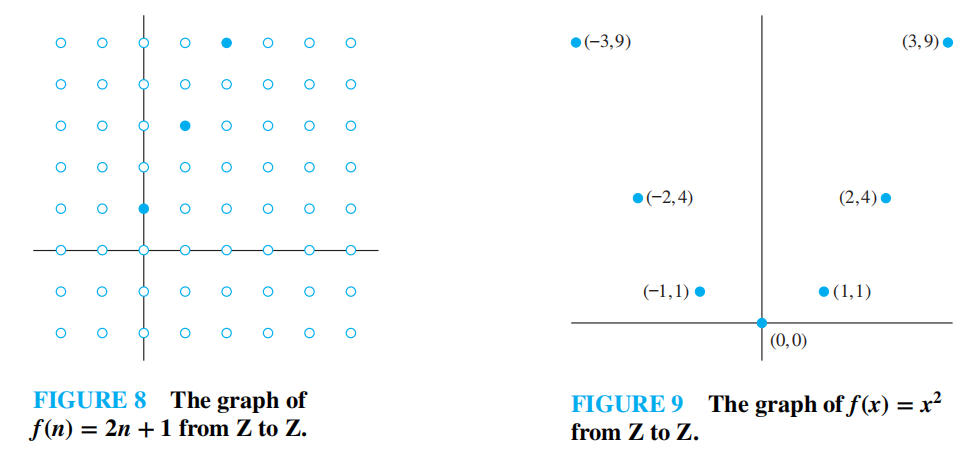
函数 \(f\) 的图象 (graph) 是一个有序对的集合 \(\{(a, b) | a \in A \text{ and } f(a) = b\}\)

🌰：

Some Important Functions⚓︎

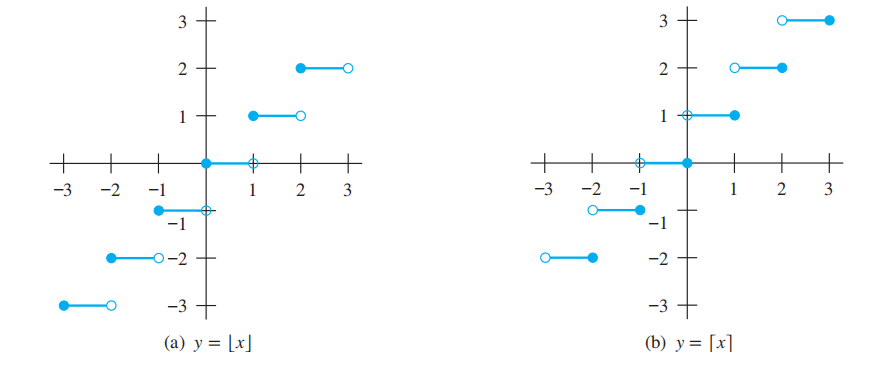
• 底函数 (floor function)：\(\lfloor x \rfloor\)，取不大于 \(x\) 的最大整数
• 顶函数 (ceiling function)：\(\lceil x \rceil\)，取不小于 \(x\) 的最小整数

图象：

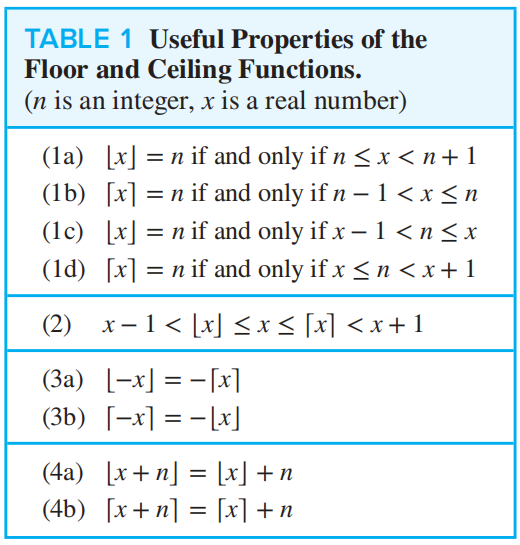
❗重要性质：

🌰：

Partial Function⚓︎

Supplements(from Exercises)⚓︎

• \(f(S \cup T) = f(S) \cup f(T) \quad \quad f(S \cap T) \subseteq f(S) \cap f(T)\)
• \(f^{-1}(S \cup T) = f^{-1}(S) \cup f^{-1}(T) \quad \quad f^{-1}(S \cap T) = f^{-1}(S) \cap f^{-1}(T)\)
• \(f^{-1}(\overline{S}) = \overline{f^{-1}(S)}\)
• 特征函数 (Characteristic function)：\(f_S: U \rightarrow \{0, 1\}\)，当 \(x\) 在 \(S\) 中时，\(f_S(x) = 1\)，否则 \(f_S(x) = 0\)
• 对于函数 \(f: A \rightarrow B\)，\(|A| = |B|\)，\(f\) 为单射函数的充要条件是 \(f\) 为满射函数
• 集合 \(S\) 是无限的充要条件是 \(S\) 的子集 \(A\) 与 \(S\) 是双射关系

Sequences and Summations⚓︎

Sequences⚓︎

序列 (sequences)：一个从整数集合（通常是 \(\{0, 1, 2, \dots\}\) 或 \(\{1, 2, 3,\dots\}\)）映射到某个集合 \(S\) 的函数，一般用 \(\{a_n\}\) 表示一个序列（不要和集合的记号弄混）

一些特殊序列：

• 等比数列 (geometric progression)：\(a, ar, ar^2, \dots, ar^n, \dots\) 其中\(a\)被称为首项，\(r\) 被称为公比
• 等差数列 (arithmetric progression)：\(a, a + d, a + 2d, \dots, a + nd, \dots\) 其中\(a\)被称为首项，\(d\) 被称为公差
• 字符串 (string)：包含字符的有限序列，可用 \(a_1, a_2, \dots, a_n\) 标记
  • 应用：位串
  • 长度 (length)：字符串包含项的个数
  • 空串 (empty string)：长度为 0，记作 \(\lambda\)

Recurrence Relations⚓︎

递推关系 (recurrence relations)：一个用于表示 \(a_n\) 的表达式，由它前面的项 \(a_0, a_1, \dots, a_{n - 1}\) 构成

如果一个序列能够满足递推关系，那这个序列被称为solution( 通解？)

因为序列的首项前面没有东西，因此需要起始条件 (initial conditions)才能使递推关系生效

斐波那契数列 (Fibonacci sequence)：起始条件为 \(f_0 = 0, f_1 = 1\)，且满足递推关系 \(f_n = f_{n - 1} + f_{n - 2}, n = 2, 3, 4, \dots\)

闭合公式 (closed formula)：一个能够解出递推关系及其起始条件的公式

求解方法：

注：更多的技巧见 Chap 8，现在仅介绍简单的方法

迭代 (iteration)：

• 前代 (forward substitution)：从首项开始代入递推关系，直至 \(a_n\) 项
• 回代 (backward substitution)：从 \(a_n\) 项开始往回代，直到首项 \(a_1\)

我们使用迭代大致猜出这个序列的通解，还需要通过数学归纳法 (mathematical induction)检验，这将在 Chap 5 讲解

Special Integer Sequences⚓︎

有时，我们只知道一个序列的前面几项，但是通过一些技巧，我们也能判断出该序列的 solution：

• 该序列是否出现过相同的值，如果有的话，出现了多少次？
• 该序列的项是否通过对前面某些项的相加得到？
• 该序列的项是否通过对前面某些项的相乘得到？
• 该序列的项是否通过对前面某些项的某种组合？
• 该序列是否有周期性
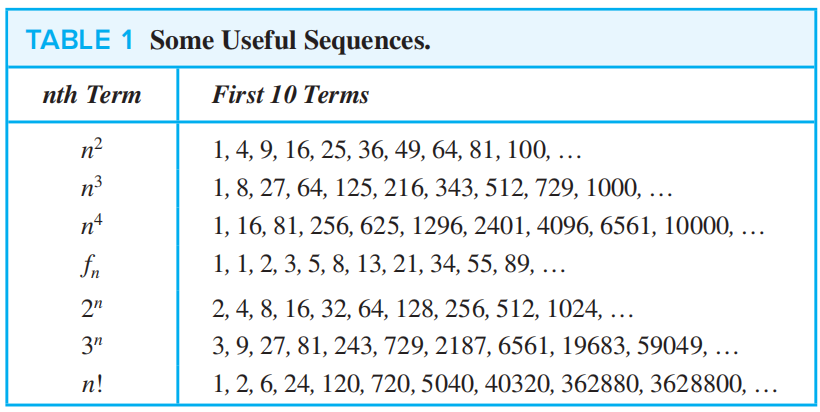
• 该序列是否与我们所熟知的一些序列（见下表）有关

Summations⚓︎

这里没什么东西好说，可能有点用的就是下面这张表👇

Supplements(from Exercises)⚓︎

• telescoping( 套管式？)：\(\sum\limits_{j = 1}^n(a_j - a_{j - 1}) = a_n - a_0\)
• 累积：\(\prod\limits_{j = m}^n a_j\)

Cardinality of Sets⚓︎

The Cardinality of a Finite Set⚓︎

• 基数

• 容斥原理

拓展：

一共有 \(C^1_n + C^2_n + \dots + C^n_n = 2^n - 1\) 项

注：Chap 8 还会详细介绍

Extend to Infinite Set⚓︎

当且仅当 \(A\) 与 \(B\) 存在双射的关系，集合 \(A\) 与 \(B\) 基数相等（这样就不用具体比较集合的大小）

• 如果集合 \(A \rightarrow B\) 存在单射的关系，则 \(|A| \le |B|\)
• 如果 \(|A| \le |B|\) 且 \(|A| \ne |B|\)，则 \(|A| < |B|\)

Countable Sets⚓︎

如果一个集合：

• 是有限集
• 或者，与正整数集\(\mathbb{Z}^+\) 有相同的基数的无限集

则这个集合是可数的 (countable)，否则是不可数的 (uncountable)

可数集合的基数 \(|S|\) 用 \(\aleph_0\) 表示

⭐判断方法：当能够列出以序列 (sequence) 元素为集合的所有元素（即双射关系 \(f: Z^+ \rightarrow {a_n}\)，有 \(a_1 = f(1), a_2 = f(2), \dots, a_n = f(n), \dots\)），一个无限集是可数的

例题

Even numberHibert's Grand HotelIntegersRational numbersStringPrograms

补充

• 如果奇 / 偶数的房间不能动，也能满足要求
• 如果增加一个一样的Grand Hotel，则原来酒店里的人能占满两个酒店的所有房间
• 如果有可数的无限个大巴来到酒店，且每辆大巴都有可数的无限个人，则能确保所有人（大巴上的人和原来酒店的人）都在酒店房间里

Uncountable Sets⚓︎

定理 1：如果集合 \(A\) 和 \(B\) 是可数的，则 \(A \cup B\) 也可数

定理 2(SCHRODER-BERNSTEIN THEOREM)：如果 \(|A| \le |B|\) 且 \(|B| \le |A|\)，则 \(|A| = |B|\)。也就是说，如果 \(A \rightarrow B\) 是单射的，\(B \rightarrow A\) 也是单射的，则 \(A\) 与 \(B\) 有双射的

• 反过来也成立
• 看似简单的定理，证明起来一点也不简单，但结论挺好记的😁

❗其他定理 / 结论：

• \((0, 1)\) 之间的实数不可数
• 所有实数都不可数

证明

用到Cantor diagonalization argument( 康托对角化论证 )

来自习题的补充：

• 不存在这样的无限集，它的基数小于可数集合的基数
• \(A, B\) 为两个集合，且 \(A \subset B \rightarrow |A| \le |B|\)
• \(A, B\) 为两个集合，\(A\) 不可数且 \(A \subseteq B \rightarrow B\) 不可数
• 可数集合的子集也是可数的
• \(|A| = |B| \rightarrow |P(A)| = |P(B)|\)
• \((|A| = |B|) \wedge (|C| = |D|) \rightarrow |A \times C| = |B \times D|\)
• \((|A| = |B|) \wedge (|B| = |C|) \rightarrow |A| = |C|\)
• \((|A| \le |B|) \wedge (|B| \le |C|) \rightarrow |A| \le |C|\)
• \(A\) 是可数集合，且存在满射 \(f: A \rightarrow B\)，则 \(B\) 也是可数集合
• 如果 \(A\) 是无限集合，则存在一个可数的无限子集
• 不存在这样的无限集合 \(A\)，使得 \(|A| < |\mathbb{Z}^+| = \aleph_0\)

• 一个包含元素为从正整数映射到 \(\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\) 的函数的集合是不可数的

• ( 来自历年卷 ) 存在可数无限集 \(A\)，使得存在一个双射：\(A \rightarrow A \times A\)

  例子：康托配对函数，虽然它是一个 \(\mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}\) 的双射函数，但双射函数的反函数也是双射的，这就符合上面的结论了

Applications⚓︎

• 如果一个计算机程序能够找到这个函数的值，则称该函数为可计算的 (computable)，否则被称为不可计算 (uncomputable)

• 幂集的基数总是大于它对应的一般集合的基数

• \(|P(Z^+)| = |R| = c\)

参考：阿列夫 (\(\aleph\)) 数

• 连续统假设 (continuum hypothesis)：不存在这样的基数 \(a\)，使得 \(\aleph_0 < a < \aleph_1\)

Matrices⚓︎

虽然划掉了（考试不考），但这里还是稍微提一下基本概念

更新：关系和图论会用到这部分的知识

矩阵 (matrix)：\(\mathbf{A} = \begin{bmatrix}a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix}\)，可简写为 \(\mathbf{A} = [a_{ij}]\)

相等：当且仅当两个矩阵的规模相同（行、列数相同）且每个位置的元素都相等时，两个矩阵相等

加法：当矩阵 \(\mathbf{A}, \mathbf{B}\) 均为 \(m \times n\) 的矩阵时，\(\mathbf{A} + \mathbf{B} = [a_{ij} + b_{ij}]\)

矩阵加法满足交换律、结合律

乘法：当矩阵 \(\mathbf{A}\) 的规模为 \(m \times k\)，矩阵 \(\mathbf{B}\) 的规模为 \(k \times n\) 时，\(\mathbf{AB} = [c_{ij}]\)，其中 \(c_{ij} = \sum\limits_{t = 1}^ka_{it}b_{tj}\)

注意：矩阵乘法有结合律和分配律，但交换律不成立

单位矩阵 (identity matrix)：\(\mathbf{I}_n = \begin{bmatrix}1 & 0 & \dots & 0 \\ 0 & 1 &\dots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \dots & 1\end{bmatrix} = [\delta_{ij}]\)，其中 \(\delta_{ij}= \begin{cases}1 & \text{if } i = j, \\ 0 & \text{if } i \ne j.\end{cases}\)

性质：对于规模为 \(m \times n\) 的矩阵 \(\mathbf{A}\)，\(\mathbf{AI}_n = \mathbf{I}_m\mathbf{A} = \mathbf{A}\)

幂：\(\mathbf{A}^0 = \mathbf{I}_n, \quad \quad \mathbf{A}^r = \underbrace{\mathbf{AAA} \dots \mathbf{A}}_{r \text{ times}}\)

转置 (transpose)：规模为 \(m \times n\) 的矩阵 \(\mathbf{A} = [a_{ij}]\) 的转置矩阵为 \(\mathbf{A}^t = [b_{ij}]\)，规模为 \(n \times m\)，其中 \(b_{ij} = a_{ji}\)

对称矩阵 (symmetric matrix)，对于方阵\(\mathbf{A}\)，如果 \(\mathbf{A} = \mathbf{A}^t\)，则 \(\mathbf{A}\) 为对称矩阵（\(\mathbf{A}\) 内的元素关于主对角线对称）

零一矩阵 (zero-one matrix)：元素仅为 0 或 1 的矩阵（与布尔运算紧密相关）

对于两个规模均为 \(m \times n\) 零一矩阵 \(\mathbf{A} = [a_{ij}], \mathbf{B} = [b_{ij}]\)

• 并 (join)：\(\mathbf{A} \vee \mathbf{B}\)，每个元素为 \(a_{ij} \vee b_{ij}\)
• 交 (meet)：\(\mathbf{A} \wedge \mathbf{B}\)，每个元素为 \(a_{ij} \wedge b_{ij}\)

对于两个零一矩阵 \(\mathbf{A}\)（规模为 \(m \times k\)）和 \(\mathbf{B}\)（规模为 \(k \times n\)），

• 布尔积 (Boolean product)：\(\mathbf{A} \odot \mathbf{B}\)（规模为 \(m \times n\)），每个元素 \(c_{ij} = \bigvee\limits_{t = 1}^k (a_{it} \wedge b_{tj})\)
• 布尔幂 (Boolean power)：\(\mathbf{A}^{[r]} = \underbrace{\mathbf{A} \odot\mathbf{A} \odot\mathbf{A} \odot \dots \odot\mathbf{A}}_{r \text{ times}}\)，规定 \(\mathbf{A}^{[0]} = \mathbf{I}_n\)

Supplements(from Exercises)⚓︎

对角矩阵 (diagonal matrix)：对于 \(n \times n\) 方阵 \(\mathbf{A} = [a_{ij}]\)，如果当 \(i \ne j\) 时，\(a_{ij} = 0\) 成立，则 \(\mathbf{A}\) 为对称矩阵

逆矩阵 (inverse)：如果 \(\mathbf{A}, \mathbf{B}\) 为 \(n \times n\) 的方阵，且 \(\mathbf{AB} = \mathbf{BA} = \mathbf{I}_n\)，则称 \(\mathbf{B}\) 为 \(\mathbf{A}\) 的逆矩阵，记作 \(\mathbf{B} = \mathbf{A}^{-1}\) 性质： \((\mathbf{A}^n)^{-1} = (\mathbf{A}^{-1})^n\)

利用矩阵解线性方程组（略）

评论区