Chap 6 Counting⚓︎

The Basics of Counting⚓︎

Basic Counting Principles⚓︎

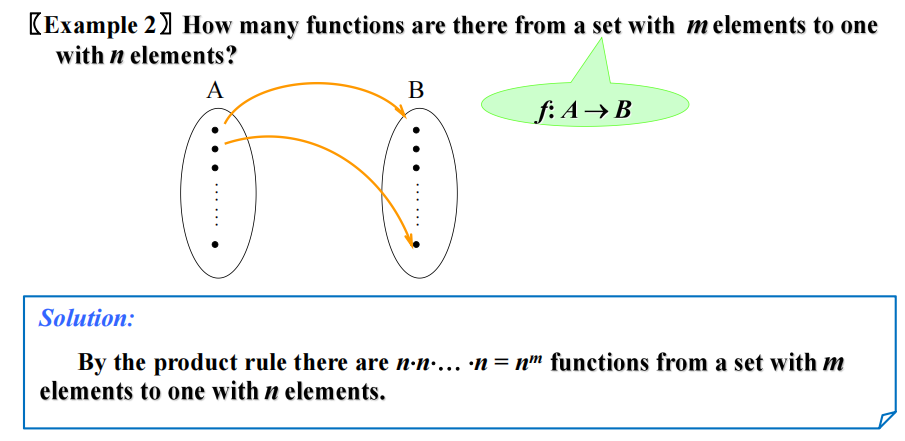
乘积法则 (THE PRODUCT RULE)：假设一个流程可以被分成两个阶段，如果有 \(n_1\) 种方法完成第一个阶段，且对于完成第一个阶段的每一种方法，有 \(n_2\) 种对应的方法完成第二个阶段，那么就有 \(n_1n_2\) 种方法完成整个流程。

拓展版本：假设一个流程可以被分成一系列阶段 \(T_1, T_2, \dots, T_m\)。如果每个阶段 \(T_i, i = 1, 2, \dots, m\) 有 \(n_i\) 种方法完成（不论前面的任务是怎么完成的），那么就有 \(n_1n_2 \dots n_m\) 种方法完成整个流程。

例题

计数函数 (counting functions) 计数单射函数 (counting one-to-one funcitons) 计数有限集合的子集 (counting subsets of a finite set)

如果 \(|A| = n\)，那么 \(|P(A)| = 2^n\)

证明：

如果 \(A_1, A_2, \dots, A_n\) 是有限集合，那么它们的笛卡尔积的元素个数等于这些集合元素个数的乘积，即：

\[|A_1 \times A_2 \times \dots \times A_m| = |A_1| \cdot |A_2| \cdot \dots \cdot |A_m|\]

和法则 (THE SUM RULE)：如果一个任务既要被包含 \(n_1\) 步的方法完成，也要被包含 \(n_2\) 步的方法完成，且 \(n_1\) 步形成的集合与 \(n_2\) 步形成的集合不相交，则总共需要 \(n_1 + n_2\) 步来完成该任务。

拓展版本：假设一个任务要被包含 \(n_1\) 步的方法、包含 \(n_2\) 步的方法……包含 \(n_m\) 的方法完成，且这些步骤形成的集合两两不相交，那么完成这个任务的总步数为 \(n_1 + n_2 + \dots + n_m\)。

因此，对于两两互不相交的集合，我们可以得到以下公式： $$ |A_1 \cup A_2 \cup \dots \cup A_m| = |A_1| + |A_2| + \dots + |A_m| \text{ when } A_i \cap A_j = \emptyset \text{ for all } i, j $$

More Complex Counting Problems⚓︎

例题

计算可能的密码个数计算 IP 地址 (IPv4) 个数

注：IPv4(32 位 ) 地址已经耗尽，IPv6(128 位 ) 的出现解决 IP 地址不足的问题

The Subtraction Rule (Inclusion-Exclusion for Two Sets)⚓︎

减法法则 (THE SUBTRACTION RULE)：如果一个任务既要 \(n_1\) 步完成，也要 \(n_2\) 步完成，则完成任务的总步数为：$n_1 + n_2 - $ 这 2 个不同方法包含的相同步骤数。

减法法则又被称为容斥原理 (principinclusion-exclusion)

🌰

The Division Rule⚓︎

除法法则 (THE DIVISION RULE)：如果一个任务有 \(n\) 种方法完成，那么对于每种方法 \(w\)，有且仅有 \(d\) 种方法与 \(w\) 等价，因此完成该任务共需 \(\dfrac{n}{d}\) 步

注：这里表述有些问题，可能会误导读者，推荐理解下面的表述

另外形式的表述 ( 容易理解一点😊)：

• 集合版本：如果一个有限集合 \(A\) 是由 \(n\) 个两两不相交的子集构成的并集，且每个子集有 \(d\) 个元素，那么 \(n = \dfrac{|A|}{d}\)
• 函数版本：如果 \(f: A \rightarrow B\)，\(A, B\) 均为有限集合，且 \(\forall y \in B\)，有且仅有 \(d\) 个 \(x \in A\)，使得 \(f(x) = y\)，那么 \(|B| = \dfrac{|A|}{d}\)

🌰

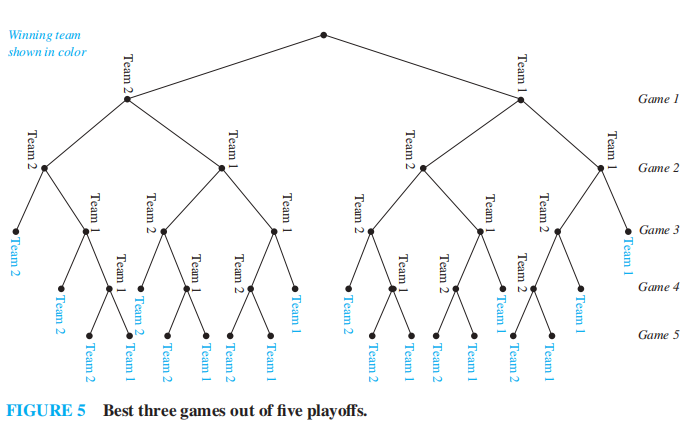
Tree Diagrams⚓︎

我们可以使用树状图 (tree diagram)解决简单的计数问题：

• 用分支表示每种可能的选择
• 用叶子表示每种可能的结果

我的理解：其实就是枚举法，只能用于数据规模较小的情况

例题

例 1 例 2 例 3

The Pigeonhole Principle⚓︎

定理 1——鸽巢原理 (THE PIGEONHOLE PRINCIPLE)：如果 \(k\) 为正整数，有 \(k+1\) 个或更多的物体放入 \(k\) 个箱子中，那么至少存在一个箱子包含 2 个或多个物体。

鸽巢原理又被称为狄利克雷抽屉原理 (Dirchlet drawer principle)

推论 1：一个从具有 \(k+1\) 或更多元素的集合映射到具有 \(k\) 个元素的集合的函数不是单射的

🌰

• 这里的 1, 11, 111 等数都是十进制的，没有二进制！
• 那两个余数相同的数相减，得到的数一定是 n 的倍数 ( 同余的定义 )，且仅由 0 和 1 构成

The Generalized Pigeonhole Principle⚓︎

定理 2——广义鸽巢原理 (THE GENERALIZED PIGEONHOLE PRINCIPLE)：如果 \(N\) 个物体放入 \(k\) 个箱子里，则至少有一个箱子里至少容纳 \(\lceil \dfrac{N}{k} \rceil\) 个物体

证明

用函数形式表示：对于一个函数 \(f: A \rightarrow B\)，如果 \(\lceil \dfrac{|A|}{|B|} \rceil = i\)，那么存在元素 \(a_1, a_2, \dots, a_i \in A\)，使得 \(f(a_1) = f(a_2) = \dots = f(a_i) = b \in B\)

🌰

Some Elegant Applications of the Pigeonhole Principle⚓︎

例题

例 1例 2例 3

注：\(2^{k_i}q_i \le 2n\)

来自课后习题，是对例 2 的补充和提升

问题答案

• 子序列 (subsequence)：包含一些原始序列的项并保持原来的顺序的序列
• 严格递增 (strictly increasing)：如果序列中的每一项都大于前一项
• 严格递减 (strictly decreasing)：如果序列中的每一项都小于前一项

定理 3：具有 \(n^2+1\) 个不同实数的序列包含一个长度为 \(n+1\) 的子序列，满足严格递增或严格递减

证明

例题

这个例子反映了鸽巢原理在拉姆齐理论 (Ramsey theory)的应用

拉姆齐数 (Ramsey number)\(R(m, n)\)（\(m, n \ge 2, m, n \in \mathbf{N}^+\)）：派对中最小的人数，满足其中要么有 \(m\) 个相互的朋友，要么有 \(n\) 个相互的敌人（假设派对中的每一对人要么是朋友要么是敌人）。它具有以下性质：

• \(R(m, n) = R(n, m)\)
• \(R(2, n) = n\)

参考：wiki

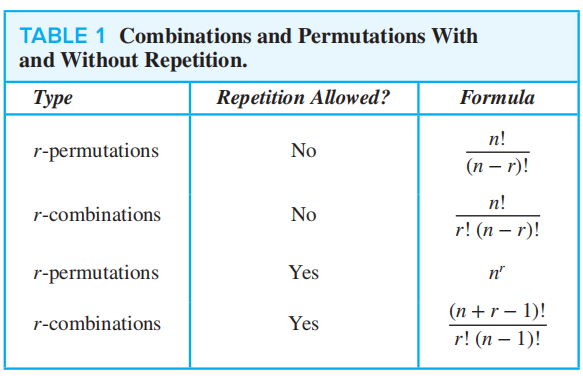
Permutations and Combinations⚓︎

Permutations⚓︎

对一组不同对象的排列 (permutation)是对这些对象的有序安排。

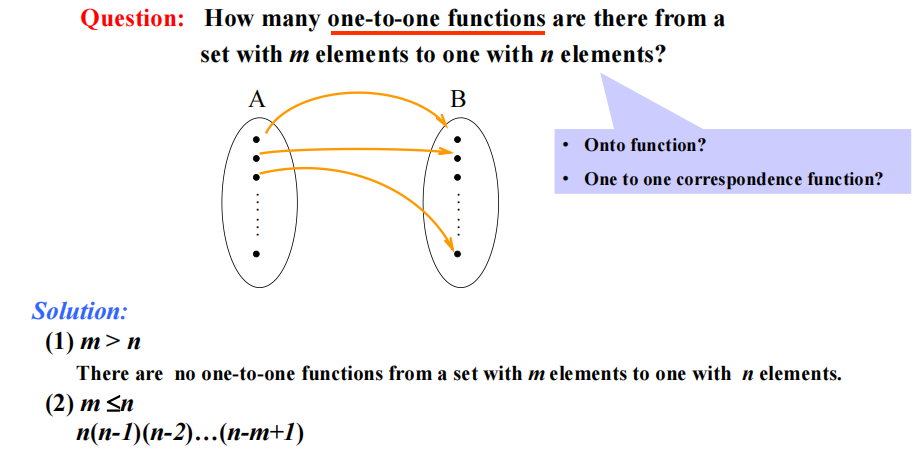
对集合中 \(r\) 个元素的有序安排被称为 \(r\)排列 (\(r\)-permutation)，记作 \(P(n, r)\)

定理 1：如果 \(n\) 是正整数，整数 \(r\) 满足 \(1 \le r < n\)，那么 $$ P(n, r) = n(n - 1)(n - 2)\dots (n - r + 1) $$

注：\(P(n, 0) = 1\)

推论 1：如果 \(n, r\) 为整数，满足 \(0 \le r \le n\)，则 \(P(n, r) = \dfrac{n!}{(n - r)!}\)

🌰

Combinations⚓︎

对包含 \(n\) 个元素的集合的 \(r\)组合 (\(r\)-combination)是从集合对 \(r\) 个元素的无序选择，记作 \(C(n, r)\)

有时也记作 \(\left( \begin{array}{cccc}n \\ r\end{array} \right)\)，被称为二项式系数 (binomial coefficient)，这将在下一节中讲到

定理 2：对于 \(n\) 个元素的集合的 \(r\) 组合 (\(n\) 为非负整数，且整数 \(r\) 满足 \(0 \le r \le n\))，等于 $$ C(n, r) = \dfrac{n!}{r!(n - r)!} $$

• 观察到 \(C(n, r) = \dfrac{P(n, r)}{P(r, r)} = \dfrac{n(n - 1) \dots (n - r + 1)}{r!}\)
• 在手工运算时，需要通过消去分子分母的公因数来简化计算

推论 2：令 \(n, r\) 为非负整数，满足 \(r \le n\)，则 \(C(n, r) = C(n, n - r)\)

定义：对于一个恒等式的组合证明法 (combinatorial proof)分为两类：

• 算两次证明法 (double counting proof)：使用计数参数来证明等号两边对同样的物体进行计数，但采用不同的方法
• 双射证明法 (bijective proof)：证明在通过等号两边的计数得到的对象集合之间存在双射关系

🌰用组合证明法来证明推论 2：

Supplements(from Exercises)⚓︎

\(n\) 的循环 \(r\) 排列 (circular \(r\)-permutation of \(n\))：\(n\) 个人中的 \(r\) 个围着圆桌坐下，每个座位认为是一样的

Binomial Coefficients and Identities⚓︎

The Binomial Theorem⚓︎

二项表达式 (binomial expression)：两项之和，比如 \(x + y\)（这些项也可以是常量和变量之积）

定理 1——二项式定理 (THE BINOMIAL THEOREM)：令 \(x, y\) 为变量，\(n\) 为非负整数，则

可以使用组合证明法证明，具体见教材 \(P_{438}\)

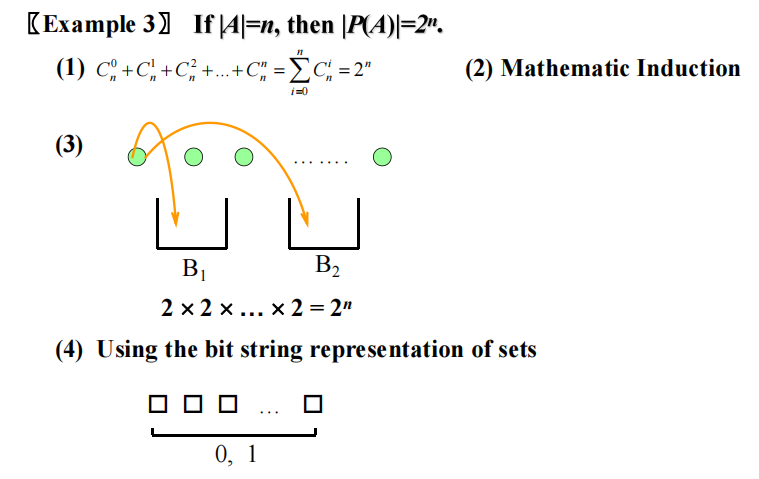
推论 1：令 \(n\) 为非负整数，则 \(\sum\limits_{k = 0}^n\left( \begin{array}{cccc}n \\ k\end{array}\right) = 2^n\)

推论 2：令 \(n\) 为正整数，则 \(\sum\limits_{k = 0}^n(-1)^k\left( \begin{array}{cccc}n \\ k\end{array}\right) = 0\)

这个推论表明：

上面两个定理均可用组合证明法证明，具体见教材 \(P_{439}\)

推论 3：令 \(n\) 为非负整数，则 \(\sum\limits_{k = 0}^n 2^k\left( \begin{array}{cccc}n \\ k\end{array}\right) = 3^n\)

Pascal's Identity and Triangle⚓︎

定理 2——帕斯卡恒等式 (PASCAL'S INDENTITY)：令 \(n, k\) 为正整数，满足 \(n \ge k\)，则

注：

• 该定理也可以用组合证明法证明，具体见教材 \(P_{440}\)
• 该定理可以用来递归定义二项式系数

帕斯卡三角形 (Pascal's triangle)，又称杨辉三角

Other Identities Involving Binomial Coefficients⚓︎

定理 3——范德蒙德恒等式 (VANDERMONDE'S IDENTITY)：令 \(m, n, r\) 为非负整数，且 \(r\) 不超过 \(m\) 和 \(n\)，则

推论 4：如果 \(n\) 为非负整数，那么

定理 4：令 \(r, n\) 为非负整数，且满足 \(r \le n\)，则

Supplements(from Exercises)⚓︎

• 如果整数 \(k, n\) 满足 \(1 \le k \le n\)，那么 \(\left( \begin{array}{cccc}n \\ k\end{array}\right) \le \dfrac{n^k}{2^{k - 1}}\)
• 六边形恒等式 (hexagon identity)：如果整数 \(k, n\) 满足 \(1 \le k < n\)，那么 \(\left( \begin{array}{cccc}n - 1\\ k - 1\end{array}\right)\left( \begin{array}{cccc}n \\ k + 1\end{array}\right)\left( \begin{array}{cccc}n + 1\\ k\end{array}\right) = \left( \begin{array}{cccc}n - 1\\ k\end{array}\right)\left( \begin{array}{cccc}n \\ k - 1\end{array}\right)\left( \begin{array}{cccc}n + 1\\ k + 1\end{array}\right)\)
• 如果 \(k, r, n\) 为非负整数且 \(r \le n, k \le r\)，则 \(\left( \begin{array}{cccc}n \\ r\end{array}\right)\left( \begin{array}{cccc}r \\ k\end{array}\right) = \left( \begin{array}{cccc}n \\ k\end{array}\right)\left( \begin{array}{cccc}n - k \\ r - k\end{array}\right)\)
• 朱世杰恒等式 (hockeystick identity)：\(\sum\limits_{k = 1}^r\left( \begin{array}{cccc}n + k \\ k\end{array}\right) = \left( \begin{array}{cccc}n + r + 1\\ r\end{array}\right)\)，其中 \(n, r\) 为正整数
• 如果 \(n\) 为正整数，那么 \(\left( \begin{array}{cccc}2n \\ 2\end{array}\right) = 2\left( \begin{array}{cccc}n \\ 2\end{array}\right) + n^2\)
• \(\sum\limits_{k = 1}^nk\left( \begin{array}{cccc}n \\ k\end{array}\right) = n2^{n - 1}\)
• \(\sum\limits_{k = 1}^nk\left( \begin{array}{cccc}n \\ k\end{array}\right)^2 = n\left( \begin{array}{cccc}2n - 1\\ n - 1\end{array}\right)\)

Generalized Permutations and Combinations⚓︎

Permutation with Repetition⚓︎

定理 1：对包含 \(n\) 类对象的集合进行 \(r\) 排列，如果允许重复，则总数为 \(n^r\)

Combination with Repetition⚓︎

定理 2：对包含 \(n\) 类对象的集合进行 \(r\) 组合，如果允许重复，则总数为 \(C(n - 1 + r, r) = C(n - 1 + r, n - 1)\)，记作 \(H_n^r\)

例题

例 1 例 2 例 3

对于 (1)，\(x_i \ge 2\) 意味着每个小块至少有两个星号，一共有 4 个小块，因此剩下的星号个数为 16 - 4 *2 = 8 个，然后对这 8 个星号和 3 根竖线进行 \(r\) 组合

总结：

Permutation with Indistinguishable Objects⚓︎

定理 3：对 \(n\) 个物体进行排列，其中有 \(n_1\) 个属于类型 1 的物体，\(n_2\) 个属于类型 2 的物体，\(\dots, n_k\) 个属于类型 \(k\) 的物体，则排列种数为 \(\dfrac{n!}{n_1!n_2!\dots n_k!}\)

注：\(n = \sum\limits_{j = 1}^kn_j\)

Distributing Objects into Boxes⚓︎

不难想到，很多计数问题都可以抽象为计算将物体放入箱子的方法个数。现在让我们来看一下这两种情况：

• 可区分的 (distinguishable, labeled)：每个物体或箱子都是不同的
• 不可区分的 (indistinguishable, unlabeled)：可以把物体或箱子看成是相同的

对于物体和箱子，都有可能具备上述两种情况中的一种，因此共有以下四种情况，其中前两者可以用闭合公式 (closed formula)来表述

闭合公式：可以用有限步的运算，求解包含数字、变量、函数值的表达式

Distinguishable Objects and Distinguishable Boxes⚓︎

定理 4：将 \(n\) 个可区别的物体放入 \(k\) 个可区分的箱子中 ( 因此 \(n_i\) 表示放入第 \(i\) 个箱子里的物体个数，\(i = 1, 2, \dots, k\))，则方法个数为 \(\dfrac{n!}{n_1!n_2!\dots n_k!}\)

不难发现，定理 3 和定理 4 之间存在双射关系

🌰

Indistinguishable Objects and Distinguishable Boxes⚓︎

结论：将 \(r\) 个不可区分的物体放入 \(n\) 个可区分的箱子的方法数为 \(C(n - 1 + r, n - 1)\) 种

注：这类问题和对具有 \(n\) 元素集合的可重 \(r\) 组合之间存在双射关系

🌰

Distinguishable Objects and Indistinguishable Boxes⚓︎

正如前文所言，没有一种闭合公式能够求解将 \(n\) 个可区分物体放入 \(j\) 个不可区分的箱子的方法数。但是，有一种数可以用来求解这类问题——第二类斯特林数 (Stirling numbers of the second kind)，记作 \(S(n, j)\)，它表示将 n 个可区分物体放入 j 个不可区分的箱子，且每个箱子非空的方法数。它有以下性质：

• \(S(r, 1) = S(r, r) = 1 (r \ge 1)\)
• \(S(r, 2) = 2^{r - 1} - 1\)
• \(S(r, r - 1) = C(r, 2)\)
• \(S(r + 1, n) = S(r, n - 1) + nS(r, n)\)
• 可以将 \(S(n, j)\) 看作将具有 \(n\) 个元素的集合划分为 \(j\) 个不相交的子集的方法数

• 利用容斥原理，可以得到 \(S(n, j) = \dfrac{1}{j!}\sum\limits_{i = 0}^{j - 1}(-1)^j\left( \begin{array}{cccc}j \\ i\end{array}\right)(j - i)^n\) 在Chap 8中，我们会利用满射函数的个数与第二类斯特林数之间的双射关系得到更便于记忆的公式 ( 满射函数的个数就是利用容斥原理推出来的 )。

• 将 \(n\) 个可区分物体放入 \(k\) 个不可区分的箱子的方法数为 \(\sum\limits_{j = 1}^kS(n, j) = \sum\limits_{j = 1}^k\dfrac{1}{j!}\sum\limits_{i = 0}^{j - 1}(-1)^j\left( \begin{array}{cccc}j \\ i\end{array}\right)(j - i)^n\)

  求和是因为这里采用了分类讨论的思想，分为：保证 1 个箱子非空的情况，保证 2 个箱子非空的情况，...，保证 k 个箱子非空的情况。

第一类斯特林数用的不多，感兴趣的可以见最后的 Supplements

例题

例 1 例 2

Indistinguishable Objects and Indistinguishable Boxes⚓︎

可以将这类题看作：求解至多 \(k\) 个非递增顺序排列的整数之和等于 \(n\) 的所有可能情况数，即 \(a_1 + a_2 + \dots + a_k = n\)，其中 \(a_1, a_2, \dots, a_k\) 为正整数，满足 \(a_1 \ge a_2 \ge \dots \ge a_k\) ，称\(a_j\ (j \in [1, k])\)为将正整数\(n\)划分为\(j\)个正整数的隔板 (partition)，记 \(p_k(n)\) 为将 \(n\) 划分为至多 \(k\) 个正整数的隔板个数。那么将 \(n\) 个不可区分的对象放入 \(k\) 个不可区分的箱子的方法数即为 \(p_k(n)\)

注：没有闭合公式能够求解这类问题

🌰

Supplements(from Exercises)⚓︎

• 多项式定理 (Multinomial Theorem)：如果 \(n\) 为正整数，则

其中 \(C(n;n_1, n_2, \dots, n_m) = \dfrac{n!}{n_1!n_2! \dots n_m!}\)

Generating Permutations and Combinations⚓︎

Generating Permutations⚓︎

：按词典序 (lexicographic/dictionary ordering)列出所有 \(n\) 个元素的排列情况

由于时间问题，具体原理就不分析了，直接贴上算法的伪代码

Generating Combinations⚓︎

利用位串，具体原理也不分析了

Supplements(from Exercises)⚓︎

另一种生成组合的方法是利用康托数 (Cantor digits)，具体略

Supplements⚓︎

• 无符号第一类斯特林数 (signless Stirling number of the first kind)：记作 \(c(n, k)\)，其中整数 \(n, k\) 满足 \(1 \le k \le n\)，它等于为 \(n\) 个人分配 \(k\) 个圆桌上的座位，使得至少有一个人有座位的方法数。对于两种方法，如果每个人都有相同的左右邻居，则认为这两种方法是一样的

评论区