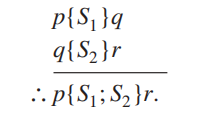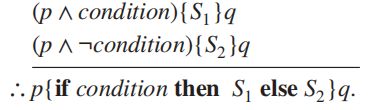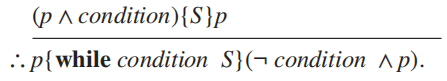Chap 5 Induction and Recursion⚓︎

Mathematical Induction⚓︎

Mathematical Induction⚓︎

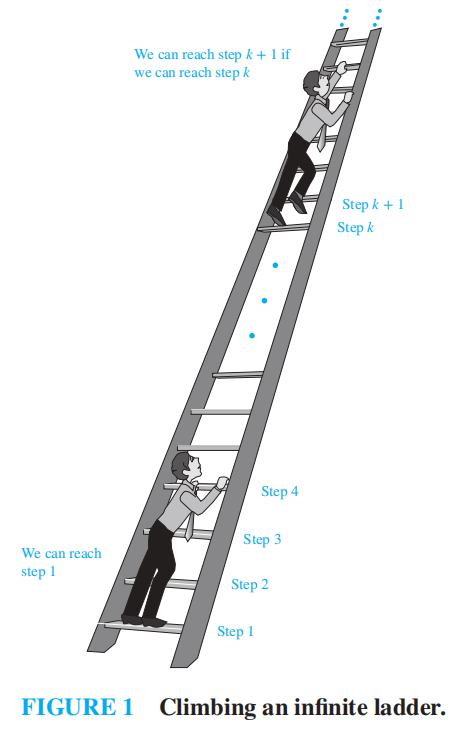
数学归纳法 (mathematical induction)：证明对于所有正整数 \(n\)，命题函数 \(P(n)\) 均为真

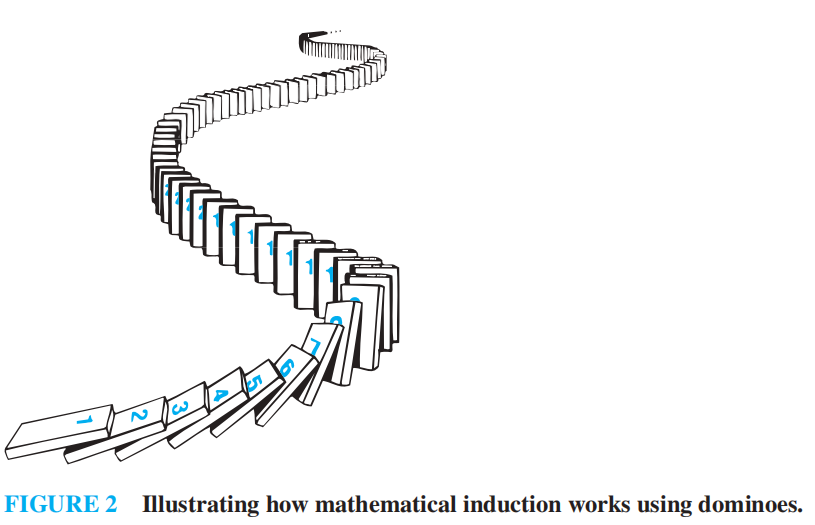
数学归纳法原理 (PRINCIPLE OF MATHEMATICAL INDUCTION)

• 基本步骤 (BASIS STEP)：验证 \(P(1)\) 为真
• 归纳步骤 (INDUCTIVE STEP)：证明对于所有正整数 \(k\)，条件语句 \(P(k) \rightarrow P(k + 1)\) 为真

为了完成归纳步骤，我们需要假设 \(P(k)\) 为真 ( 这被称为归纳假设 (inductive hypothesis))，然后在这一假设下，证明 \(P(k + 1)\) 为真

用推理规则 (inference rules) 表达上述原则：\((P(1) \wedge \forall k (P(k) \rightarrow P(k + 1))) \rightarrow \forall nP(n)\)

注意：我们假设 \(P(k)\) 为真，不是对于所有正整数 \(k\) 而言，而是想通过这个假设证明 \(P(k + 1)\) 为真，因此通过数学归纳法得到的证明不是循环论证

形象记忆数归

• 无限高的梯子

• 多米诺骨牌

Why Mathematical Induction is Valid⚓︎

可以用良序性 (well-ordering property)证明数学归纳法的合法性

良序性：对于一个包含正整数的集合，它的每个非空子集都有最小的元素

Choosing the Correct Basis Step⚓︎

有时，基本步骤可能不是从 1 开始，而是从整数 \(b\) 开始的。因此在基本步骤中，要先验证 \(P(b)\) 为真

Guidelines for Proofs by Mathematical Induction⚓︎

The Good and the Bad of Mathematical Induction⚓︎

• Good：证明猜想 (Conjecture)的一大利器
• Bad：不能用来发现新的定理，而且无法从证明过程中看出定理的本质所在

  也许你在根本没有理解某个定理的情况下，也能通过数学归纳法证明出该定理

Examples of Proofs by Mathematical Induction⚓︎

例题 ( 请最好看完所有例子 )

证明求和公式证明不等式证明与整除相关的结论证明与集合相关的结论证明与算法相关的结论数学归纳法的创意用法

见教材 \(P_{336-340}\)

见教材 \(P_{340-342}\)

补充知识点

调和数 (harmonic numbers)：\(H_j = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \dots + \dfrac{1}{j}\)

结论：\(H_{2^n} \ge 1 + \dfrac{n}{2}\)( 证明过程见 \(P_{342}\))

调和级数 (harmonic series)：\(1 + \dfrac{1}{2} + \dfrac{1}{3} + \dots + \dfrac{1}{n} + \dots\) 它是发散的 (divergent)

见教材 \(P_{342-344}\)

这里我放了 1 个例题，虽然课件里没讲，但我觉得这题挺不错的，尤其是归纳步骤中的最后一步

见教材 \(P_{344-346}\)

见教材 \(P_{346-347}\)

书上的例题是证明第 3 章中安排讲座问题使用的贪心算法是否得到的是最优解，但我有点看不太懂😕

见教材 \(P_{347-349}\)

• 基本步骤：因为只有 3 个人，画一个三角形可以较为直观地解释，这里就不详细展开了 ~

• 递归步骤：

  • case 1: 如果有人向 A 或 B 丢馅饼，那么除了 A，B 之外的 2k + 1 个人只有 2k 个馅饼，由归纳假设知，那 2k + 1 个人中至少有一个人没有被馅饼砸中
  • case 2: 如果没有人向 A 或 B 丢馅饼，则剩下 2k + 1 个人满足归纳假设的条件，在他们之中至少存在一个幸存者 S，他不仅没被那 2k 个人砸中，也不会被 A 或 B 砸中 ( 因为 A 和 B 没被原来 2k + 1 个人砸中，说明 A 和 B 之间的距离是他们离其他人的最近距离，因此 A 和 B 会互相扔馅饼 )

综上，至少有 1 位幸存者

Mistaken Proofs by Mathmatical Induction⚓︎

使用数学归纳法时，请确保基本步骤 (basis step)和归纳步骤 (inductive step)都正确！！！

Supplements(from Exercises)⚓︎

• 伯努利不等式 (Bernoulli's inequality)：如果 \(h > -1\)，对于所有非负整数 \(n\)，满足 \(1 +nh \le (1 + h)^n\)
• 假设 \(a, b\) 为实数，且 \(0 < b < a\)，如果 \(n\) 为正整数，则 \(a^n - b^n \le na^{n - 1}(a - b)\) 成立
• 对于正整数 \(n\)，满足 \(1 + \dfrac{1}{\sqrt 2} + \dfrac{1}{\sqrt 3} + \dots + \dfrac{1}{\sqrt n} > 2(\sqrt{n + 1} - 1)\)
• 如果 \(n\) 是非负整数，则 \(H_{2^n} \le 1 + n\)
• \(H_1 + H_2 + \dots + H_n = (n + 1)H_n - n\)
• 当 \(n \ge 3\) 且 \(n\) 为整数时，对于有 \(n\) 个元素的集合，它有 \(\dfrac{n(n - 1)(n - 2)}{6}\) 个包含 3 个元素的子集

Strong Induction and Well-Ordering⚓︎

注：数学归纳法、强归纳法、良序性三者是等价的

Strong Induction⚓︎

强归纳法 (STRONG INDUCTIVE)

• BASIS STEP：验证 \(P(1)\) 为真（与数学归纳法一样）
• INDUCTIVE STEP：证明对于所有正整数 \(k\)，条件语句 \([P(1) \wedge P(2) \wedge \dots \wedge P(k)] \rightarrow P(k+1)\) 为真

强归纳法的归纳假设是对于 \(j = 1, 2, \dots, k, P(j)\) 为真。因此它相比数学归纳法更加灵活

强归纳法也被称为数学归纳法第二原理 (second principle of mathematical induction)或完全归纳法 (complete induction)。因此数学归纳法也被称为不完全归纳法 (incomplete induction)（但这个名称不太符合它，因为数学归纳法是一个“完全”的方法）

Examples of Proofs Using Strong Induction⚓︎

🌰

将 k+1 分解为两个因数 a 和 b 后，因为 a、b 在归纳假设的范围内，因此它们满足是质数或多个质数的乘积的条件，所以 k+1 也满足该条件

Using Strong Induction in Computational Geometry⚓︎

计算几何 (computational geometry)：离散数学的分支，研究关于几何图形的计算问题

定义：

• 多边形 (polygon)：由一系列线段 \(s_1, s_2, \dots, s_n\)( 它们被称为边 (sides)) 构成的封闭几何图形

  如果没有两条非连续的边相交，那么被称为简单 (simple)多边形

• 顶点 (vertex)：多边形中每对连续的边 \(s_i, s_{i + 1}(i = 1, 2, \dots, n - 1)\)( 也包括 \(s_n\) 和 \(s_1\)) 上的公共端点

• 每个简单多边形将平面划分成 2 个区域：
  • 内部 (interior)：曲线内的所有点
  • 外部 (exterior)：曲线外的所有点
• 凸 (convex)多边形：任意两个顶点间的线段位于多边形的内部或边界上。否则被称为凹 (nonconvex)多边形
• 对角线 (diagonal)：在简单多边形中，连接两个非连续顶点的线段
  • 内部对角线 (internal diagonal)：如果除了端点外完全在内部的对角线

定理 1：对于一个有 \(n\)(\(n\) 为 \(\ge 3\) 的整数 ) 条边的简单多边形，它能被划分为 \(n - 2\) 个三角形

证明（需要下面的引理 1）

引理 1：每一个至少有 4 条边的多边形有一个内部对角线

Proofs Using the Well-Ordering Property⚓︎

良序性的定义

🌰

假设 \(r \ge d\)，因为 \(a = dq_0 + r\)，所以 \(a - d(q_0 + 1) = r - d \ge 0\)，因此存在 \(q\) 和 \(r\)，使得 \(0 \le r < d\) 成立（且 \(q\) 和 \(r\) 是唯一的）

Supplements(from Exercises)⚓︎

• 对于所有正整数对 \(n, k\)，可以通过以下步骤证明 \(P(n, k)\) 为真 ( 以下均省略 " 对于所有正整数 \(n, k\)")

  • \(P(1, 1)\) 为真，且 \(P(n, k) \rightarrow [P(n + 1, k) \wedge P(n, k + 1)]\) 为真
  • \(P(1, k)\) 为真，且 \(P(n, k) \rightarrow P(n + 1, k)\) 为真
  • \(P(n, 1)\) 为真，且 \(P(n, k) \rightarrow P(n, k + 1)\) 为真

• 数学归纳法、强归纳法、良序性三者等价的证明：

  • 用良序性证明数学归纳法：见上面
  • 用良序性证明强归纳法：
    
  • 用数学归纳法证明良序性：
    

Recursive Definition and Structural Induction⚓︎

Recursively Defined Functions⚓︎

递归 ( 或归纳 ) 定义 (recursive/inductive definition)：比如下面对函数的定义 ( 其域为非负整数 )

• BASIS STEP：具体说明自变量为 0 时函数的值
• 递归步骤 (RECURSIVE STEP)：给定一个规则——通过前面更小的整数下的函数值，得到在某个整数下的函数值

递归定义函数是严格定义的 (well defined)，也就是说，

• 对于给定的任意正整数，我们都能使用定义的两部分 ( 即基本步骤和递归步骤 )，找到对应正整数的函数值
• 无论我们怎样使用定义的两部分，总能得到相同的值

对于某些递归定义函数，前 \(k\) 个正整数对应的函数值已经给出；并且给定了一个规则：通过一些或全部前 \(k\) 个整数下的函数值，得到在某个整数下的函数值。这种也是严格定义的函数，它遵循强归纳。比如前面讲到的斐波那契数便是如此。下面将运用斐波那契数得到一些性质：

应用：证明欧几里得算法 \(\text{gcd}(a, b)\) 中的除法次数为 \(O(\log b)\)

定理 1——拉梅定理 (LAME'S THEOREM)：令 \(a, b\) 为正整数且 \(a \ge b\)，那么在欧几里得算法中，得到 \(\text{gcd}(a, b)\) 所需除法次数小于等于 5 倍的 \(b\) 的十进制位数

证明

因为 \(b\) 的十进制位数为 \(\lfloor \log_{10} b \rfloor + 1 \le \log_{10}b + 1\)，由定理 1 知除法次数小于等于 \(5(\log_{10} b + 1)\)。又因为 \(5(\log_{10} b + 1)\) 是 \(O(\log b)\)，因此可以得到上述结论。

Recursively Defined Sets and Structures⚓︎

递归定义集合 (recursively definition of sets)分为两部分：

• 基本步骤 (basis step)：具体说明初始的一组元素
• 递归步骤 (recursive step)：提供让已知的新元素进入该集合的规则

递归定义也可包含一个排他规则 (exclusion rule)：递归定义的集合不包含除了在基本步骤中说明的元素，或者通过递归步骤产生的元素之外的元素。

🌰

递归定义在研究字符串 (strings)时发挥重要作用，我们有以下定义：

• 来自字母表 \(\Sigma\) 的字符串，是一个由来自 \(\Sigma\) 的符号构成的有限序列。

• 来自字母表 \(\Sigma\) 的字符串集合 \(\Sigma^*\)，按照下面步骤递归定义：

  • BASIS STEP：\(\lambda \in \Sigma^*\)，\(\lambda\) 是不包含符号的空字符串
  • RECURSIVE STEP：如果 \(w \in \Sigma^*\) 且 \(x \in \Sigma\)，那么 \(wx \in \Sigma^*\)

    在递归步骤中，通过在原有字符串的末尾添加一个字符来形成新的字符串。

🌰位串的定义：

递归定义还可以用来定义关于递归定义函数中元素的运算和函数，比如下面这两个定义：

• 通过拼接 (concatenation)，将两个字符串结合起来。令 \(\Sigma\) 为符号集，\(\Sigma^*\) 为由 \(\Sigma\) 里的符号构成的字符串集。下面递归定义两个字符串的拼接运算，记作 \(\cdot\)

  • BASIS STEP：如果 \(w \in \Sigma^*\)，那么 \(w \cdot \lambda = w\)，其中 \(\lambda\) 为空字符串
  • RECURSIVE STEP：如果 \(w_1 \in \Sigma^*, w_2 \in \Sigma^*, x \in \Sigma\)，那么 \(w_1 \cdot (w_2 x) = (w_1 \cdot w_2) x\)

    \(w_1 \cdot w_2\) 通常记作 \(w_1w_2\)

• 字符串长度 (length)：记作 \(l(w)\)，满足 \(\begin{cases}l(\lambda) = 0 \\ l(wx) = l(w) + 1 \quad \text{ if } w \in \Sigma^*\text{ and } x \in \Sigma \end{cases}\)

递归定义的另一重要应用是用来定义各种类型的合式公式 (well-formed formulae)

• 命题逻辑 (propositional logic)中的合式公式：包含 \(\mathbf{T}, \mathbf{F}\)、命题变量和来自集合 \(\{\neg, \wedge, \vee, \rightarrow, \leftrightarrow \}\) 中的运算符

  • BASIS STEP：\(\mathbf{T}, \mathbf{F}, s\)，其中 \(s\) 为命题变量，它们是合式公式
  • RECURSIVE STEP：如果 \(E, F\) 是合式公式，那么 \((\neg E), (E \wedge F), (E \vee F), (E \rightarrow F), (E \leftrightarrow F)\) 也是合式公式

• 运算符 (operators)和操作数 (operands)中的合式公式：包含变量、数字、和来自集合 \(\{+, -, *, /, \uparrow\}\) 的运算符 (\(\uparrow\) 指的是指数运算 )

  • BASIS STEP：如果 \(x\) 是数字或变量，则 \(x\) 是合式公式
  • RECURSIVE STEP：如果 \(F, G\) 是合式公式，则 \((F + G), (F - G), (F *G), (F / G), (F \uparrow G)\) 是合式公式

树 (trees)也可采用递归定义（具体内容 Chap 11）

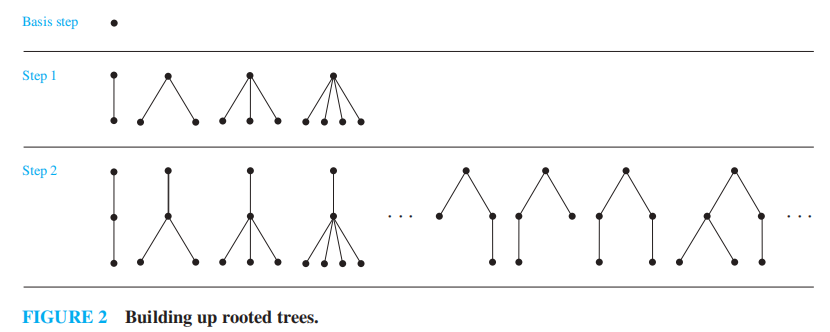
• 有根树 (rooted trees)：是一组顶点的集合，其中包含一个唯一的根节点；以及连接这些顶点的边。递归定义如下：

  • BASIS STEP：单个顶点r是一棵有根树
  • RECURSIVE STEP：假设 \(T_1, T_2, \dots, T_n\) 是不相交的有根树，它们的根节点分别为 \(r_1, r_2, \dots, r_n\)。那么新的有根树起始于一个根节点 \(r\)，该点不在 \(T_1, \dots, T_n\) 中的任何一棵树中，然后从 \(r\) 开始，向 \(r_1, \dots, r_n\) 添加边。这样就形成了一棵有根树

根据该递归定义，可以构造出无穷多棵有根树

二叉树 (binary tree)：有根树的一种特殊情况。我们给出下面两种二叉树的递归定义：

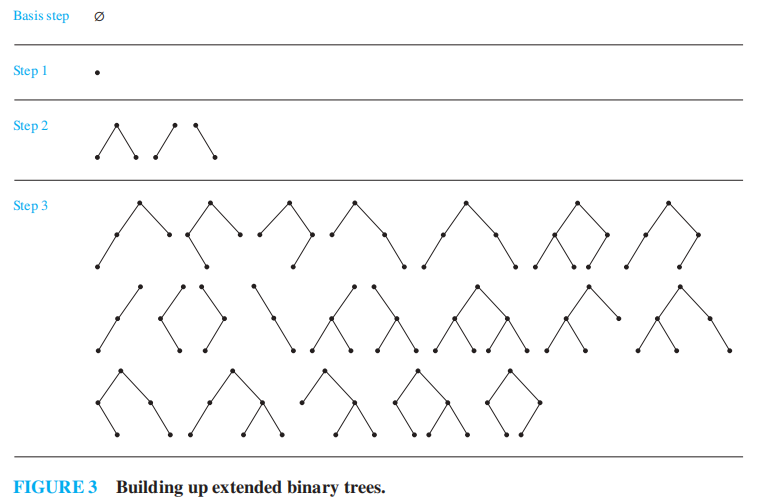
• 扩展二叉树 (extended binary tree)

  • BASIS STEP：空树是一棵扩展二叉树
  • RECURSIVE STEP：如果 \(T_1, T_2\) 是不相交的两棵（非空）扩展二叉树，那么就有一棵扩展二叉树，记作 \(T_1 \cdot T_2\)，它由一个根节点 \(r\)，以及一条从根节点连接左子树 \(T_1\) 的根节点的边，和一条连接右子树 \(T_2\) 的根节点的边

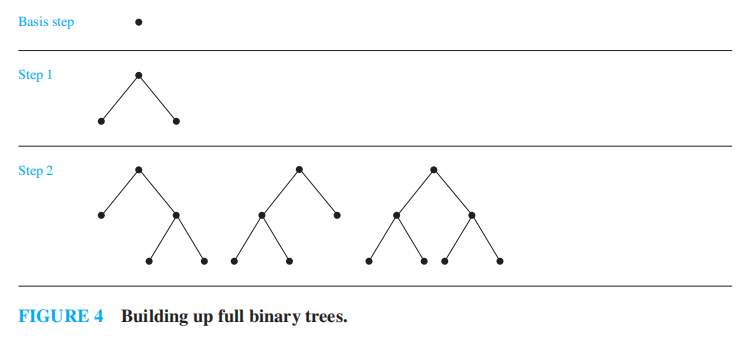
• 满二叉树 (full binary tree)

  • BASIS STEP：仅由单个顶点 \(x\) 构成一棵满二叉树
  • RECURSIVE STEP：如果 \(T_1, T_2\) 是两棵不相交的满二叉树，那么就有一棵满二叉树，记作 \(T_1 \cdot T_2\)，它由一个根节点 \(r\)，以及从根节点连接到作为左子树的 \(T_1\) 的根节点，和作为右子树的 \(T_2\) 的根节点的边

简化版：这种二叉树除了叶子节点外，其余节点要么有 2 个孩子，要么没有孩子

Structural Induction⚓︎

结构归纳法 (structural induction)：用于证明递归定义的合法性

• BASIS STEP：证明结果适用于所有在递归定义的基本步骤中说明的元素
• RECURSIVE STEP：证明如果对于每个用于在定义的递归步骤中构建新元素的元素，语句均正确，那么结果也适用于这些新构建的元素

结构归纳法的有效性可由非负整数的数学归纳法证得。

令 \(P(n)\) 表示：对于所有由 \(n\) 次或更少次来自递归定义中递归步骤的规则应用而产生的元素，结果为真

• BASIS STEP：证明 \(P(0)\) 为真
• RECURSIVE STEP：假设 \(P(k)\) 为真，那么 \(P(k + 1)\) 为真

例题

例 1 例 2 例 3

递归定义满二叉树 \(T\) 的高度 \(h(T)\)

• BASIS STEP：只有一个根节点 \(r\) 的满二叉树 \(T\) 的高度为 \(h(T) = 0\)
• RECURSIVE STEP：如果 \(T_1, T_2\) 都是满二叉树，那么满二叉树 \(T = T_1 \cdot T_2\) 的高度 \(h(T) = 1 + \max(h(T_1), h(T_2))\)

递归定义满二叉树的顶点个数 \(n(T)\)

• BASIS STEP：只有一个根节点 \(r\) 的满二叉树 \(T\) 的顶点个数 \(n(T) = 1\)
• RECURSIVE STEP：如果 \(T_1, T_2\) 都是满二叉树，那么满二叉树 \(T = T_1 \cdot T_2\) 的顶点个数 \(n(T) = 1 + n(T_1) + n(T_2)\)

定理 2：如果 \(T\) 为满二叉树，那么 \(n(T) \le 2^{h(T) + 1} - 1\)

证明

Generalized Induction⚓︎

广义归纳法 (generalized induction)用于证明关于除了整数集外，也具有良序性的集合的结论。

🌰定义一个有序的 \(\mathbb{N} \times \mathbb{N}\)，即非负整数的有序对。如果 \(x_1 < x_2\)，或者 \(x_1 = x_2\) 且 \(y_1 < y_2\)，那么 \((x_1, y_1) \le (x_2, y_2)\)，这被称为词典序 (lexicographic ordering)( Chap 9 会讲到 )。它满足良序性，这意味着我们可以递归定义 \(a_{m, n}\)，其中 \(m \in \mathbb{N}, n \in \mathbb{N}\)，见下面的具体例子👇

Supplements(from Exercises)⚓︎

关于斐波那契数的一些性质 ( 以下 \(n\) 均为正整数 )：

• \(f_1^2 + f_2^2 + \dots + f_n^2 = f_nf_{n + 1}\)
• \(f_1 + f_3 + \dots + f_{2n-1} = f_{2n}\)
• \(f_{n+1}f_{n-1} - f_n^2 = (-1)^n\)
• \(f_0f_1 + f_1f_2 + \dots + f_{2n-1}f_{2n} = f_{2n}^2\)
• \(f_0 - f_1 + f_2 - \dots - f_{2n-1} + f_{2n} = f_{2n-1} - 1\)
• 令 \(\mathbf{A} = \begin{bmatrix}1 & 1 \\ 1 & 0\end{bmatrix}\)，则 \(\mathbf{A}^n = \begin{bmatrix}f_{n + 1} & f_n \\ f_n & f_{n - 1}\end{bmatrix}\)

关于最大值和最小值函数的一些性质：

• \(\max(-a_1, -a_2, \dots, -a_n) = -\min(a_1, a_2, \dots, a_n)\)
• \(\max(a_1 + b_1, a_2 + b_2, \dots, a_n + b_n) \le \max(a_1, a_2, \dots, a_n) + \max(b_1, b_2, \dots, b_n)\)
• \(\min(a_1 + b_1, a_2 + b_2, \dots, a_n + b_n) \ge \min(a_1, a_2, \dots, a_n) + \min(b_1, b_2, \dots, b_n)\)

关于字符串：

• 字符串 \(w\) 的逆序 (reversal)记为 \(w^R\)
• \(w^i\)：拼接\(i\) 个字符串 \(w\) 后形成的新字符串

性质：

• \((w_1w_2)^R = w_2^Rw_1^R\)
• \(l(w^i) = i \cdot l(w)\)
• \((w^R)^i = (w^i)^R\)

正整数 \(n\) 的分拆 (partition)：将 \(n\) 表示为一些正整数的和，这些正整数的顺序并不重要。令 \(P_m\) 等于对于 \(m\) 不同分拆的个数，\(P_{m, n}\) 表示分拆出来的正整数不超过 \(n\)，且对于 \(m\) 不同分拆的个数

• \(P_{m, m} = P_m\)
• \(P_{m, n} = \begin{cases}1 & \text{if } m = 1 \\ 1 & \text{if } n = 1 \\ P_{m, m} & \text{if } m < n \\ 1 + P_{m, m - 1} & \text{if } m = n > 1 \\ P_{m, n - 1} + P_{m - n, n} & \text{if } m > n > 1\end{cases}\)

阿克曼函数 (Achermann's funciton)

它在递归函数理论，以及研究包含集合合并的特定算法的复杂度 ( 比如并查集 ) 中发挥重要作用，定义如下：

性质 ( 下面的字母均表示非负整数 )：

• \(A(m, n + 1) > A(m, n)\)
• \(A(m + 1, n) \ge A(m, n)\)
• \(A(i, j) \ge j\)

关于对数 ( 以 2 为底 )：

叠对数 (iterated logarithm)\(\log^*n\)：它的值为使 \(\log^{(k)}n \le 1\) 成立的最小的非负整数 \(k\)

将上面对数的定义推广至更一般的函数 \(f(n)\)（它是实数域上的单调递增函数）

叠函数 (iterated function)\(f^*_c\)：它的值为使 \(f^{(k)}n \le c\) 成立的最小的非负整数 \(k\)

Recursive Algorithm⚓︎

如果一个算法通过将问题规模减少至拥有更小输入的相同问题，那么称这个算法是递归的 (resursive)

一些例子

计算 \(\text{gcd}(a, b)\) 模指数的求解查找算法的递归版本

• 线性查找：
  
• 二分查找：
  

Proving Recursive Algorithms Correct⚓︎

通常，我们利用数学归纳法、强归纳法证明递归算法的正确性

Recursion and Iteration⚓︎

• 递归 (resursion) 法：通过连续减少计算规模，在更小的数字上求解函数
• 迭代 (iteration) 法：从一个或多个整数对应的函数值开始（基本情况），然后连续使用递归定义，找到连续的更大的数对应的函数值

🌰找到第 \(n\) 个斐波那契数的算法

• 递归版本

• 迭代版本

通过这个例子，不难看出递归和迭代算法的特征：

• 对于每个递归算法，总有等价的迭代算法
• 递归算法相比迭代算法，通常更小、更优雅、更易于理解
• 然而，迭代算法在空间和时间上的效率往往高于递归算法

The Merge Sort⚓︎

因为课上没讲（应该不会在 dm 考到），这里就直接贴上算法和定理，没有具体说明

算法实现：

引理 1：两个排好序的列表，分别有 \(m\) 和 \(n\) 个元素，将它们合并称一个有序列表所需的比较次数为 \(m + n - 1\) 次

定理 1：通过归并排序对有 \(n\) 个元素的列表排序所需的比较次数为 \(O(n \log n)\)

Supplements(from Exercises)⚓︎

快速排序 (quick sort)：要对 \(a_1, a_2, \dots, a_n\) 排序，先找到 \(a_1\)，然后形成两个子列表：第一个子列表中的所有元素小于 \(a_1\)，第二个子列表中的所有元素大于 \(a_1\)，并且分别对它们排好序。接着将 \(a_1\) 放入第一个子列表的末尾。递归重复上述步骤，直到所有子列表仅包含一项。最后通过有序地结合只包含一个元素的子列表，得到排好序的包含 \(n\) 个元素的列表

Program Correctness⚓︎

Program Verification⚓︎

如果一个程序对所有可能的输入，均产生正确的输出，那么称这个程序是正确的 (correct)

证明一个程序的正确性包含两个部分：

• 部分正确性 (partial correctness)：程序终止时能够得到正确的答案
  • 首断言 (initial assertion)：必须有输入
  • 末断言 (final assertion)：必须有输出
• 程序总是能够终止

定义：一个程序，或者程序段 \(S\)，当对于 \(S\) 的输入值，首断言 \(p\) 正确，且 \(S\) 终止，那么对于 \(S\) 的输出值，末断言 \(q\) 正确，称 \(S\) 关于 \(p\) 和 \(q\)部分正确 (partially correct)，记作 \(p\{S\}q\)（这个记号被称为霍尔三元组 (Hoare triple)）

Rules fo Inference⚓︎

运用推理规则 (rule of inference)，将程序划分为一系列的子程序，然后证明每个子程序正确，以此证明程序的正确性。

具体说明：将程序 \(S\) 拆成两个子程序 \(S_1,S_2\)，记作 \(S = S_1 ; S_2\)。假设 \(S_1\) 关于首断言 \(p\) 和末断言 \(q\) 的正确性，和 \(S_2\) 关于首断言 \(q\) 和末断言 \(r\) 的正确性已经建立。这表明：如果 \(p\) 为真且 \(S_1\) 得到执行并终止，那么 \(q\) 为真；如果 \(q\) 为真且 \(S_2\) 得到执行并终止，则 \(r\) 为真。这个规律被称为复合律 (composition rule)，并记作：

Conditional Statements⚓︎

对于以下形式的程序段：

要验证该程序段关于首断言 \(p\) 和末断言 \(q\) 正确：

• 当 \(p\) 为真且condition也为真时，\(S\) 终止后，\(q\) 为真
• 当 \(p\) 为真且condition为假时，\(q\) 为真

因此我们得到以下推理规则：

对于以下形式的程序段：

我们得到以下推理规则：

Loop Invariants⚓︎

对于以下形式的程序段：

循环不变式 (loop invariant)\(p\)：当 \(S\) 被执行时保持真值为真的断言

我们有以下推理规则：

Supplements(from Exercises)⚓︎

• 斐波那契数的一条性质：\(f_kf_n + f_{k+1}f_{n+1} = f_{n+k+1}\)
• 卢卡斯数 (Lucas numbers)的性质 (\(I_0 = 2,\ I_1 = 1,\ I_n = I_{n - 1} + I_{n - 2}, n = 2,3,4,\dots\))
  • \(f_n + f_{n+2} = I_{n+1}\)
  • \(I_0^2+I_1^2+\dots +I_n^2 = I_nI_{n+1}+2\)
• 麦卡锡 91 函数 (McCarthy 91 function) $$ M(n) = \begin{cases}n - 10 & \text{if } n > 100 \ M(M(n+11)) & \text{if } n \le 100\end{cases} $$
• 当一个集合的每个非空子集都有一个最小元素，那么称该集合是良序的 (well ordered)
• 包含所有括号平衡字符串 (balanced strings of parentheses)的递归定义：
  • \(\lambda \in B\)，\(\lambda\) 为空串
  • \((x) \in B, xy \in B\)，如果 \(x, y \in B\)
• 自我生成序列 (self-generating sequences)：由简单的递推关系和规则产生的序列
  • Golomb self-generating sequences

评论区