跳转至

Chap 2: Solutions of Equations in One Variable⚓︎

约 2546 个字 20 行代码 预计阅读时间 13 分钟

本章探讨的问题是：求 \(f(x) = 0\)（一元方程）的根 (root)。

The Bisection Method⚓︎

第一个要介绍的求根方法是二分法(bisection method)，它的思路非常简单，以微积分课程中介绍过的介值定理(intermediate value theorem) 为理论依据，通过二分不断逼近真正的根。

介值定理

如果 \(f \in C[a, b]\)（\(C\) 表示连续函数）且 \(K\) 是介于 \(f(a)\) 和 \(f(b)\) 之间的任意值，那么存在一个数 \(p \in (a, b)\)，使得 \(f(p) = K\)

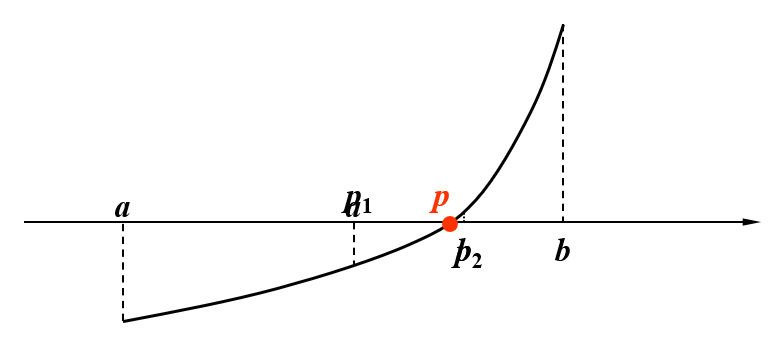
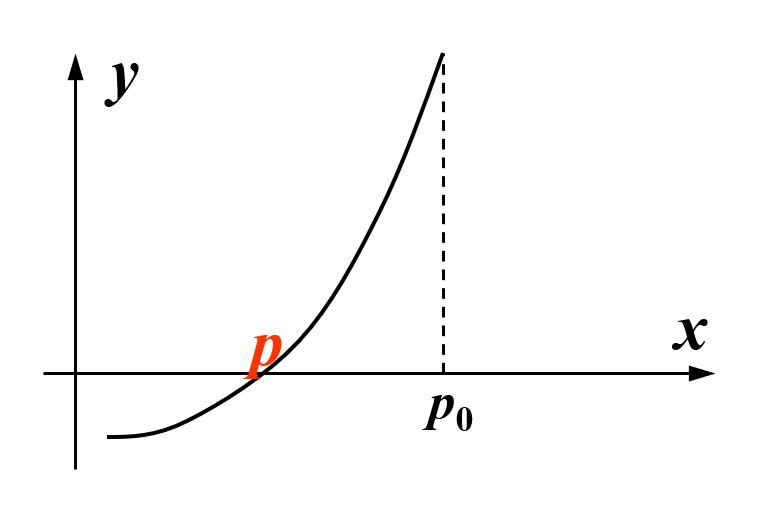
接下来基于上图来演示二分法的过程：

过程演示

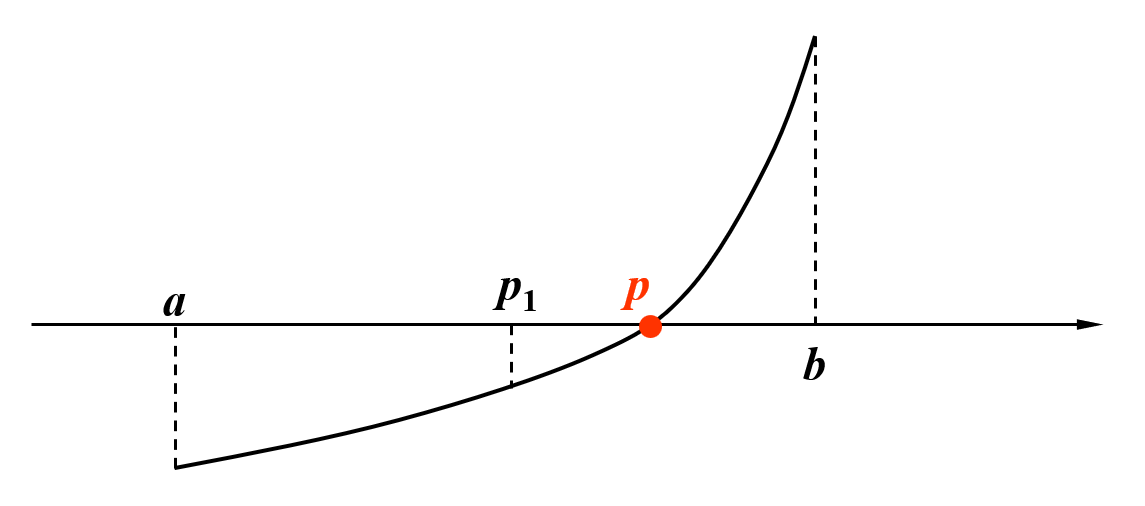
在 \(a, b\) 之间取中点 \(p_1\)。观察图像，并根据介值定理，\(f(p_1), f(b)\) 之间存在取值为 0 的情况，那么真正的根 \(p\) 一定落在 \(p_1\) 和 \(b\) 之间，所以接下来令 \(p_1\) 为下界 \(a\)，继续二分。

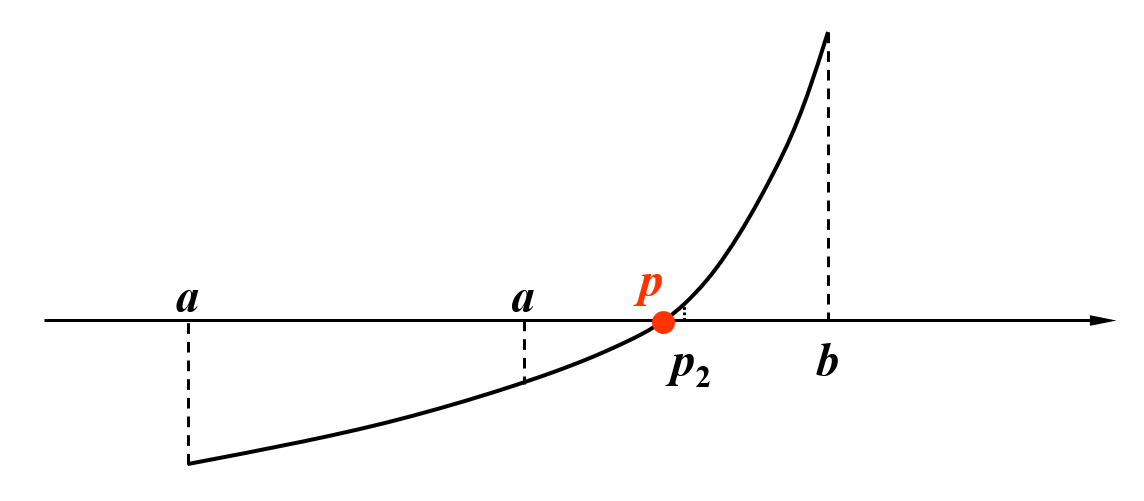
在 \(a(\text{originally }p_1), b\) 之间取中点 \(p_2\)。观察图像，并根据介值定理，\(f(a), f(p_2)\) 之间存在取值为 0 的情况，那么真正的根 \(p\) 一定落在 \(a\) 和 \(p_2\) 之间，所以接下来令 \(p_2\) 为上界 \(b\)，继续二分。

后续过程同上所述。

讨论：那么，这一迭代过程何时结束呢？

以下几种条件都可作为停止迭代的根据：

  • 绝对误差：\(|P_N - p_{N-1}| < \varepsilon\)
  • 相对误差：\(\dfrac{|p_N - p_{N-1}|}{|p_N|} < \varepsilon\)
  • 函数值：\(|f(p_N)| < \varepsilon\)

然而，使用误差作为依据的时候需要当心：因为在实践中，存在序列 \(\{p_N\}\) 发散的情况，这个时候不应该将误差作为判断依据。

定理

假设 \(f \in C[a, b]\) 且满足 \(f(a) \cdot f(b) < 0\)，那么二分法将产生一个序列 \(\{p_n\} (n = 1, 2, \dots)\)，用于逼近 \(f\) 的一个零点 \(p\)，并满足：

\[ |p_n - p| \le \dfrac{b - a}{2^n} \quad \text{when } n \ge 1 \]
证明

当 \(n \ge 1\) 时，有

\[ b_n - a_n = \dfrac{1}{2^{n-1}}(b - a) \quad \text{and} \quad p \in (a_n, b_n) \]

成立。因为 \(n \ge 1\) 时，有 \(p_n = \dfrac{1}{2}(a_n + b_n)\)，所以

\[ |p_n - p| \le \dfrac{1}{2}(b_n - a_n) = \dfrac{b - a}{2^n} \]

成立。

二分法的实现

在连续函数 \(f\) 的区间 \([a, b]\) 上寻找 \(f(x) = 0\) 的解，其中 \(f(a), f(b)\) 符号相反。

  • 输入：端点 \(a, b\)；容忍值 (tolerance) \(TOL\)；最大迭代次数 \(N_{max}\)
  • 输出：\(p\) 的近似解或失败信息
Step 1  Set i = 1;
            FA = f(a);
Step 2  while (i <= N_max) do steps 3-6
        Step 3  Set p = a + (b - a) / 2;  // computer p_i
                FP = f(p);
        Step 4  if (FP == 0) or (b - a) / 2 < TOL then Output(p);
                STOP;  // successful
        Step 5  Set i++;
        Step 6  if sign(FA) * sign(FP) > 0 then Set a = p; FA = FP;
                else set b = p;  // update a_i, b_i
Step 7  Output(Method failed after N_max iterations);  // unsuccessful
        Stop.
思考伪代码中的高亮部分

为什么取中值的代码不写成 p = (a + b) / 2，为什么判断上下界的代码不写成 FA * FP > 0？

主要是为了防止溢出(overflow)。因为无论是 a + b 还是 FA * FP，如果它们的符号一致，且数值特别大的时候，它们的和或积可能是计算机无法表示出来的东西，也就是产生了溢出的问题，此时该算法可能返回的是一个意料之外的结果，而不产生报错。所以我们需要好好关注这些细节！

对二分法的评价

优点：

  • 简单，只要求函数 \(f\) 是连续的
  • 结果总是会收敛到真正的解

缺点：

  • 收敛速度过慢，并且在计算过程中，更好的介值近似可能在不经意间被抛弃掉了
  • 不适用于寻找多根和复数根的情况

实际使用时的建议

  • 在使用二分法之前先画一幅 \(f(x)\) 的草图，先观察二分法是否可行
  • 或者用一个子程序将完整的区间划分为多个子区间 \([a_k, b_k]\)，这样的话即使 \(f(a) \cdot f(b)\)，也可以保证 \(f(a_k) \cdot f(b_k) < 0\)

Fixed-Point Iteration⚓︎

接下来介绍第二种求根方法：不动点迭代(fixed-point iteration)。首先，我们要将 \(f(x)\) 的根看作 \(g(x)\) 的不动点，即：

\[ f(x) = 0 \xLeftrightarrow{\text{equivalent}} x = g(x) \]

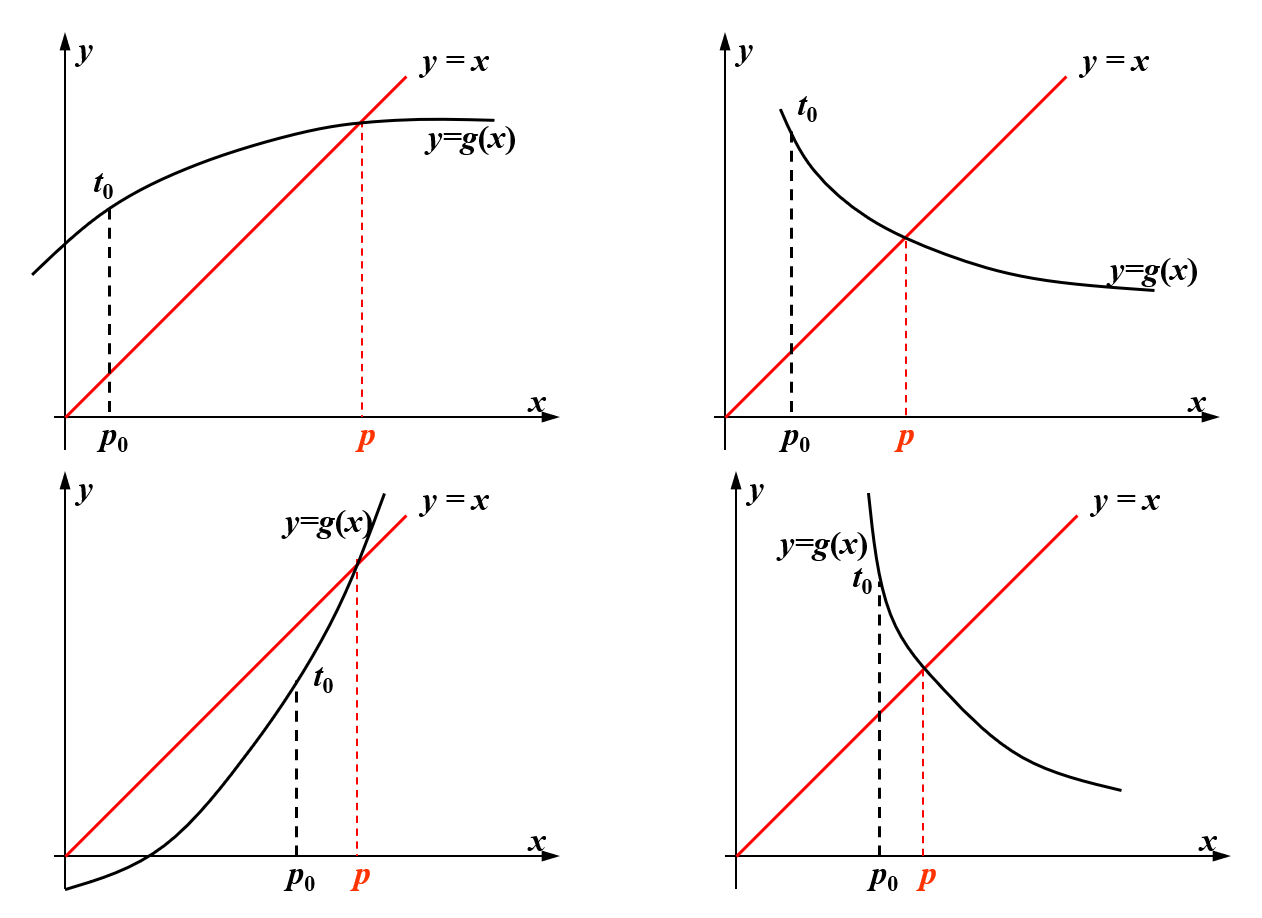
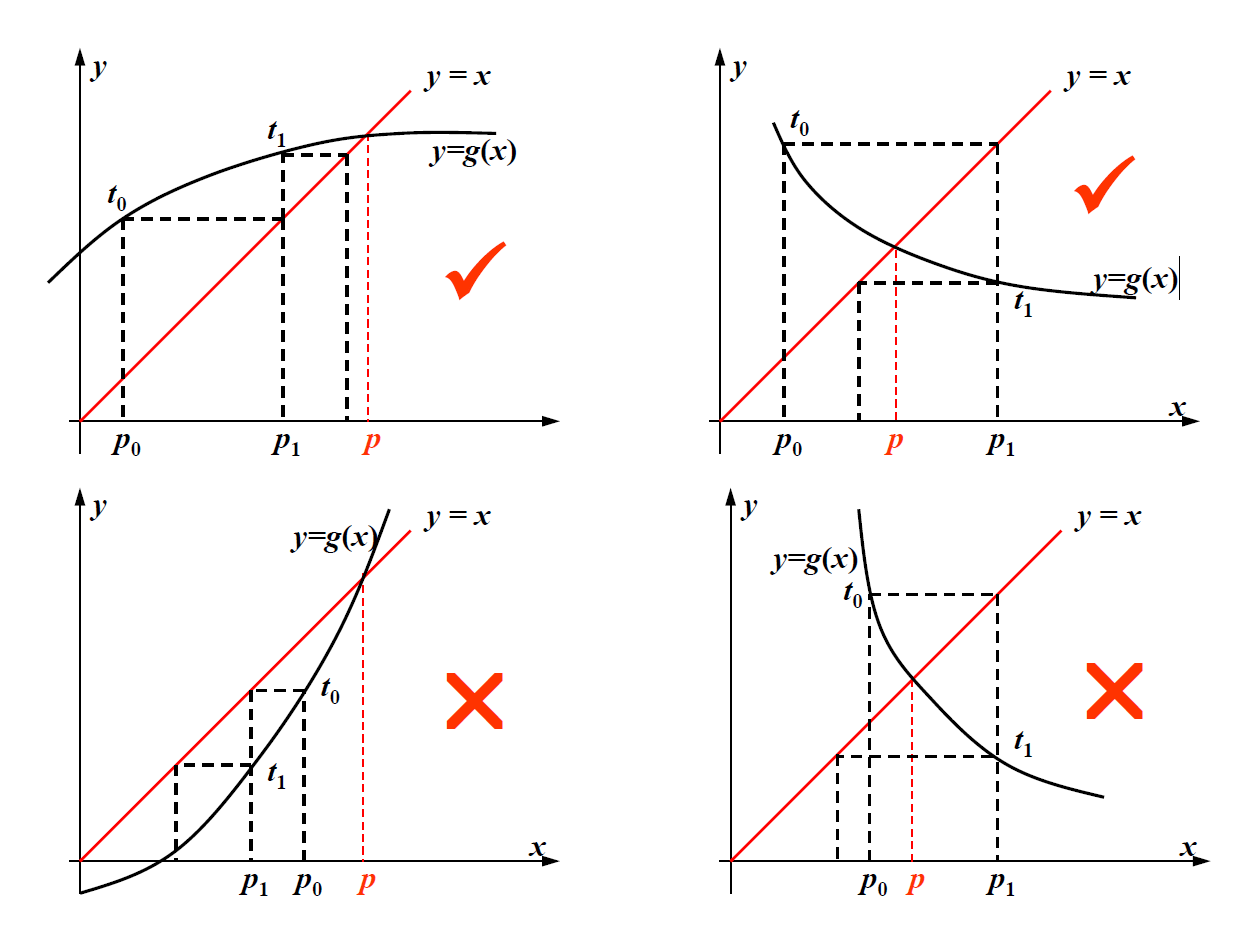
基本思路是：从初始的近似值 \(p_0\) 开始，通过 \(p_n = g(p_{n-1})\)（其中 \(n \ge 1\)），产生序列 \(\{p_n\}_{n=0}^\infty\)。如果该序列能收敛到 \(p\)，且 \(g\) 是一个连续函数，那么：

\[ p = \lim\limits_{n \rightarrow \infty} p_n = \lim\limits_{n \rightarrow \infty} g(p_{n-1}) = g(\lim\limits_{n \rightarrow \infty} p_{n-1}) = g(p) \]

看起来这个方法特别简单，貌似只需要不断的迭代，我们总能找到解。但实际上，并不是所有的 \(g(x)\) 都能做到让序列收敛，具体来看下面几个例子：

例子

判断以下几种 \(g(x)\) 中，哪个能做到收敛，为什么？

  • 这里 \(f(x) = x\)
  • 建议在阅读答案前，先自己动手画画看

让我不禁回忆起浙江高考恶心人的数列大题

不动点定理

令 \(g \in C[a, b]\)，且满足 \(\forall x \in [a, b]\)，有 \(g(x) \in [a, b]\)。并且一阶导函数 \(g'\) 存在于区间 \((a, b)\)，且满足 \(\forall x \in (a, b)\)，\(\exists\) 常数 \(k \in (0, 1)\) 使得 \(|g'(x)| \le k\) 成立。那么 \(\forall p_0 \in [a, b]\)，由 \(p_n = g(p_{n-1}), n \ge 1\) 定义的序列会收敛到位于区间 \([a, b]\) 上的唯一不动点。

证明

对于上述定理，我们需要证明三个点：

  • “不动点”：令 \(f(x) = g(x) - x\)，因为 \(a \le g(x) \le b\)，所以 \(f(a) = g(a) - a \ge 0\) 且 \(f(b) = g(b) - b \le 0\)。由介值定理知，\(f\) 一定有一个根，因此 \(g\) 有一个不动点

  • “唯一”：（用反证法证明）

    • 假设 \(p, q\) 都是 \(g\) 在区间 \([a, b]\) 上的两个不同的不动点
    • 根据均值定理(mean value theorem)，存在一个位于 \(p, q\) 的数 \(\xi\)，满足 \(g(p) - g(q) = g'(\xi)(p - q)\)
    • 因为 \(g(p) = p, g(q) = q\)，所以可以得到 \((1 - g'(\xi))(p - q) = 0\)，和已知条件矛盾，因此假设不成立，即“不动点是唯一的”结论成立

  • “收敛”：即证明 \(\lim\limits_{n \rightarrow \infty} |p_n - p| = 0\)

    • 因为 \(\forall x \in [a, b]\)，\(g(x) \in [a, b]\)，所以 \(\forall n \ge 0\)，\(p_n\) 都是有定义的

    • 因此：

      \[ \begin{align} |p_n - p| & = |g(p_{n-1}) - g(p)| = |g'(\xi)||p_{n-1} - p| \le k|p_{n-1} - p| \notag \\ & \le k^2 |p_{n-2} - p| \le \dots \le k^n|p_0 - p| \notag \end{align} \]

    • 根据条件，\(k \in (0, 1)\)，所以 \(k^n \rightarrow 0\)，因此 \(lim\limits_{n \rightarrow \infty} |p_n - p| = 0\) 成立

推论

如果 \(g\) 满足不动点定理的假设，那么用 \(p_n\)（\(\forall n \ge 1\)）近似表示 \(p\) 所产生的误差边界为：

\[ |p_n - p| \le \dfrac{1}{1 - k}|p_{n+1} - p_n| \quad \text{and} \quad |p_n - p| \le \dfrac{k^n}{1 - k} |p_1 - p_0| \]
证明
  • \(|p_{n+1} - p_n| \ge |p_n - p| - |p_{n+1} - p| \ge |p_n - p| - k|p_n - p|\)
  • \(|p_{n+1} - p_n| = |g(x_n) - g(x_{n-1})| = |g'(\xi_n)(p_n - p_{n-1})| \le k|p_n - p_{n-1}| \le \dots \le k^n |p_1 - p_0|\)
讨论：思考这两个不等式的意义
  • 前者可以用来控制计算的精度
  • 后者告诉我们：\(k\) 越小，收敛速度越快
不动点迭代的实现

给定一个初始近似值 \(p_0\)，找到 \(p = g(p)\) 的一个解。

  • 输入：初始近似值 \(p_0\)；容忍值 \(TOL\)；最大迭代次数 \(N_{max}\)
  • 输出：近似解 \(p\) 或错误信息
Step 1  Set i = 1;
Step 2  while (i <= N_max) do steps 3-6
        Step 3  Set p = g(p_0);  // compute p_i
        Step 4  if |p - p_0| < TOL then Output(p);  // successful
            STOP;
        Step 5  Set i++;
        Step 6  Set p_0 = p;  // update p_0
Step 7  Output(The method failed after N_max iterations);  // unsuccessful
例题

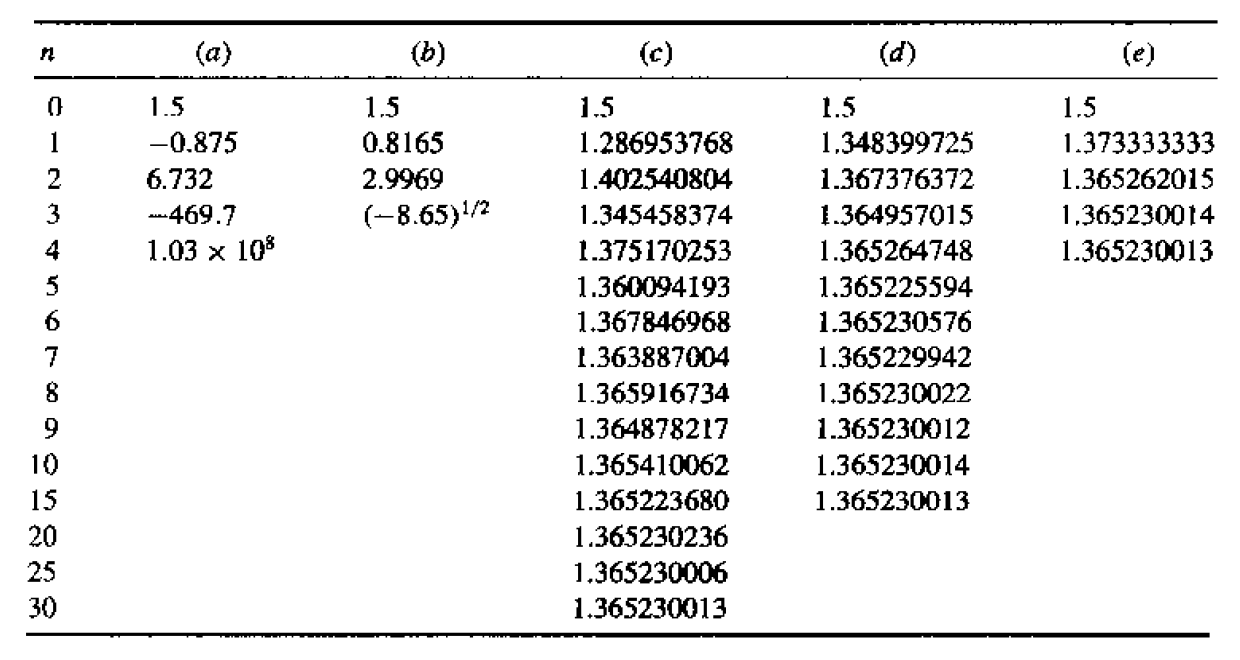
如果无脑迭代的话，会得到以下结果：

可以看到 a 和 b 不太行，c, d, e 都可以迭代下去。不行的原因分别是一个不收敛，另一个出现对负数开根号的情况。但即使是 OK 的那几个，也有一些小小的差别：

  • c. 在区间 \([1, 1.5]\) 时，\(k \approx 0.66\)
  • d. \(k \approx 0.15\)
  • e. \(k\) 更小，表现最好

Newton's Method⚓︎

最后要介绍的求根方法是牛顿法(Newton's method)，它的基本思想是使用泰勒展开式(Taylor's expansion) 来线性化一个非线性的函数。

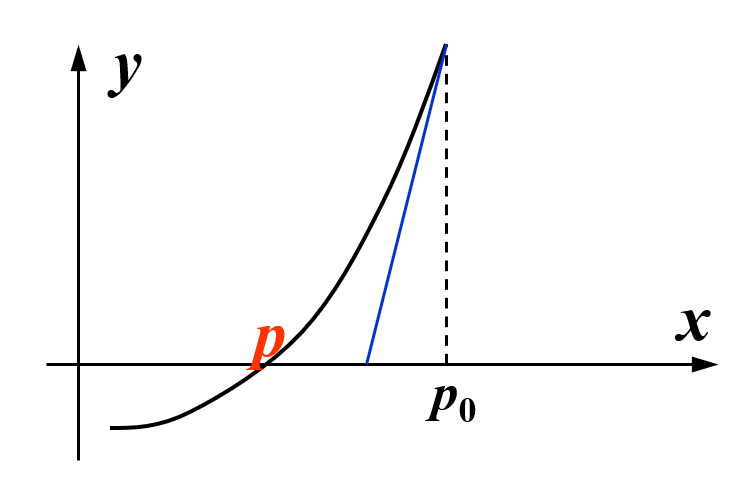
具体来说，令 \(p_0 \in [a, b]\) 为 \(p\) 的一个近似值，满足 \(f'(p) \ne 0\)。考虑以下 \(f(x)\) 关于 \(p_0\) 的泰勒多项式：

\[ f(x) = f(p_0) + f'(p_0)(x - p_0) + \dfrac{f''(\xi_x)}{2!} (x - p_0)^2 \quad \text{where } \xi_x \text{ lies between } p_0 \text{ and } x \]

假设 \(|p - p_0|\) 很小，那么 \((p - p_0)^2\) 会更小，那么：

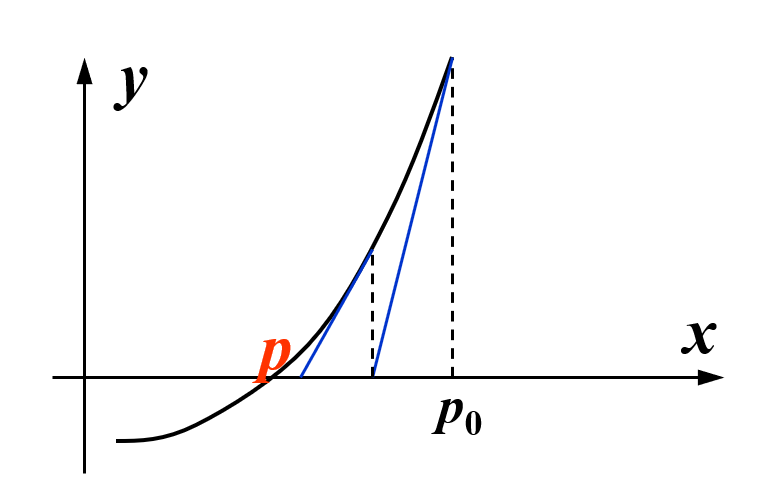
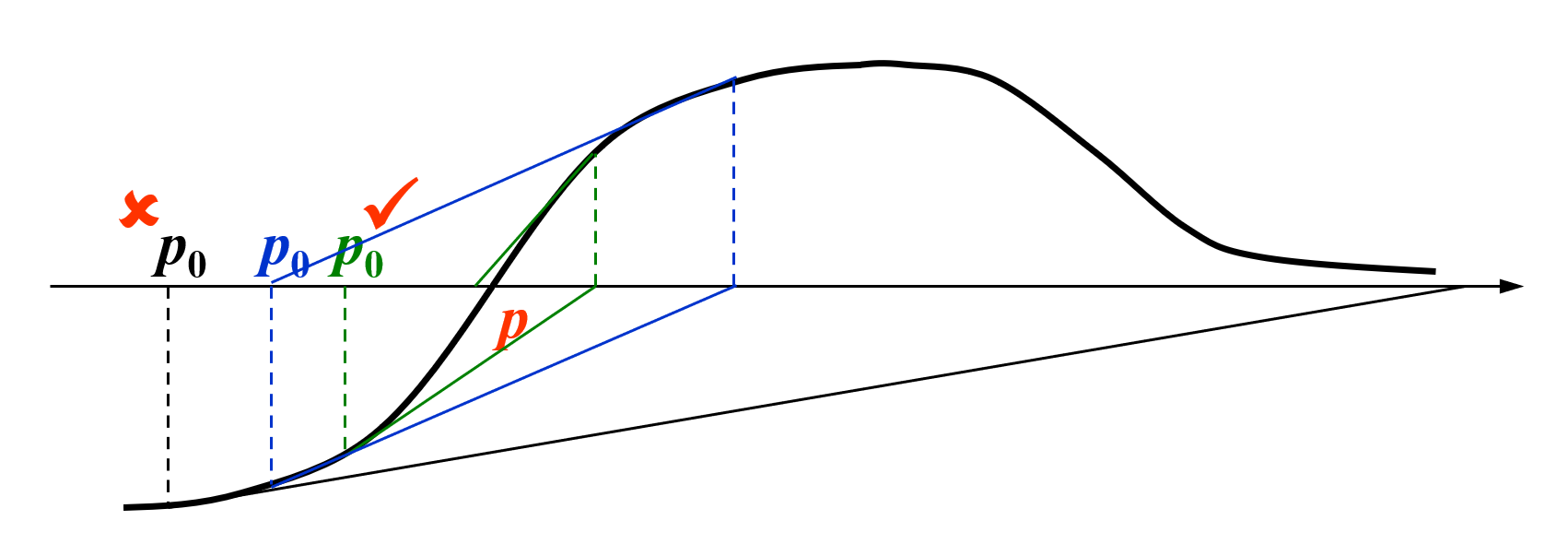
\[ 0 = f(p) \approx f(p_0) + f'(p_0) (p - p_0) \Rightarrow p \approx p_0 - \dfrac{f(p_0)}{f'(p_0)} \]
动画演示

先取一个近似值 \(p_0\)。

求该位置下的导数，然后在对应点上做一条切线，该切线与 x 轴的交点即为下一个近似值，该近似值更加接近于真实值。

从新的近似值出发，求该位置下的导数，然后在对应点上做一条切线，该切线与 x 轴的交点即为下一个近似值，该近似值更加接近于真实值。

重复上述过程，直至逼近真正的解 \(p\)。

从上述过程中，我们不难得到一下递推关系式：

\[ p_n = p_{n-1} - \dfrac{f(p_{n-1})}{f'(p_{n-1})} \quad \text{for } n \ge 1 \]

定理

令 \(f \in C^2[a, b]\)（即函数具有二阶连续导数）。如果 \(p \in [a, b]\) 满足 \(f(p) = 0\) 且 \(f'(p) \ne 0\)，那么存在一个 \(\delta > 0\)，使得牛顿法产生一个序列 \(\{p_n\} (n = 1, 2, \dots)\)，对任意近似值 \(p_0 \in [p - \delta, p + \delta]\)，该序列收敛于 \(p\)。

证明

牛顿法就是：\(p_n = g(p_{n-1}), n \ge 1\)，满足 \(g(x) = x - \dfrac{f(x)}{f'(x)}\)。我们需要回答以下问题：

  • \(g(x)\) 是否在 \(p\) 的邻近区域内连续
    • 因为 \(f'(p) \ne 0\) 且连续，所以在 \(p\) 的邻近区域内，\(f'(x) \ne 0\)
  • \(g'(x)\) 是否在 \(p\) 的邻近区域内被 \(0 < k < 1\) 约束
    • 因为 \(g'(x) = \dfrac{f(x) f''(x)}{[f'(x)]^2}\)，所以 \(g'(p) = 0\)
    • 又因为 \(f''(x)\) 连续，所以 \(g'(x)\) 很小，且在 \(p\) 的邻近区域内连续
  • \(g(x)\) 是否将 \([p - \delta, p + \delta]\) 映射到自身
    • \(|g(x) - p| = |g(x) - g(p)| = |g'(\xi)||x - p| \le k|x - p| < |x - p| < \delta\)

注意

牛顿法的收敛性取决于初始近似值的选择。如下图所示，如果选择不当的话，牛顿法就会失效：

Error Analysis for Iterative Methods⚓︎

定义

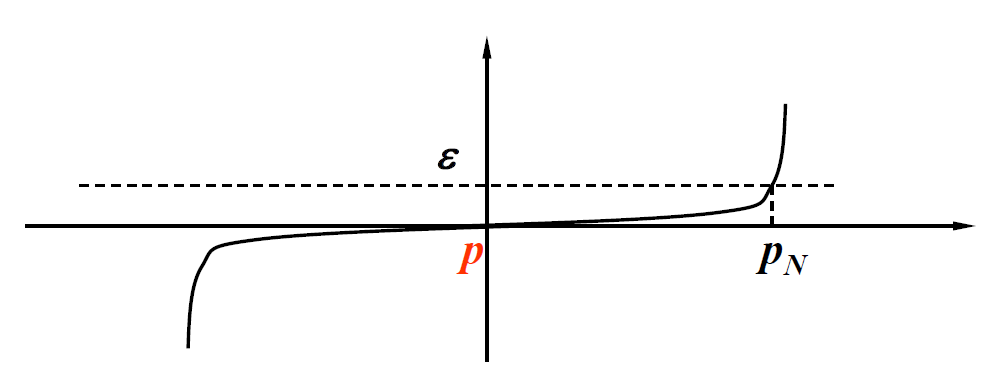
假设 \(\{p_n\} (n = 0, 1, 2, \dots)\) 是一个收敛到 \(p\) 的序列，且 \(\forall n, p_n \ne p\)。若存在正常数 \(\alpha, \lambda\)，使得：

\[ \lim\limits_{n \rightarrow \infty} \dfrac{|p_{n+1} - p|}{|p_n - p|^\alpha} = \lambda \]

成立，那么 \(\{p_n\} (n = 0, 1, 2, \dots)\) 以阶数 \(\alpha\) 收敛到 \(p\)，且渐进误差常量为 \(\lambda\)。

  • 若 \(\alpha = 1\)，那么序列是线性(linearly) 收敛的
  • 若 \(\alpha = 2\)，那么序列是二次(quadratically) 收敛的

思考

对于 \(g'(p) \ne 0\) 的迭代法，收敛的阶数是多少？

\[ \lim\limits_{n \rightarrow \infty} \dfrac{|p_{n+1} - p|}{|p_n - p|^\alpha} = \lim\limits_{n \rightarrow \infty} \dfrac{g'(\xi_n)|p_n - p|}{|p_n - p|^\alpha} = |g'(p)| \]

因此是线性收敛的。

讨论

牛顿法的收敛阶数是多少（此时 \(g'(p) = 0\)）？

通过泰勒展开式可以得到：

\[ \begin{align} 0 = f(p) & = f(p_n) + f'(p_n)(p - p_n) + \dfrac{f''(\xi_n)}{2!} (p - p_n)^2 \notag \\ \Rightarrow p & = \underbrace{p_n - \dfrac{f(p_n)}{f'(p_n)}}_{p_{n+1}} - \dfrac{f''(\xi_n)}{2! f'(p_n)}(p - p_n)^2 \Rightarrow \dfrac{|p_{n+1} - p|}{|p_n - p|^2} = \dfrac{f''(\xi_n)}{2f'(p_n)} \notag \end{align} \]

只要 \(f'(p) \ne 0\)（在一个简单根附近），那么牛顿法至少是二次收敛的。

定理

令 \(p\) 是 \(g(x)\) 的不动点。如果存在一些常量 \(\alpha \ge 2\)，使得 \(g \in C^\alpha [p - \delta, p + \delta], \textcolor{red}{g'(p) = \dots = g^{(\alpha - 1)}(p) = 0}\) 且 \(\textcolor{red}{g^{(\alpha)}(p) \ne 0}\)。那么关于 \(p_n = g(p_{n-1}), n \ge 1\) 的迭代是 \(\alpha\) 阶收敛的。

证明
\[ p_{n+1} = g(p_n) = \underbrace{g(p)}_{=p} + g'(p)(p_n - p) + \dots + \underbrace{\dfrac{g^{(\alpha)}(\xi_n)}{\alpha !}}_{=\lambda(\text{when } n \rightarrow \infty)}(p_n - p)^\alpha \]

讨论

如果根不是简单的（有重根），那么牛顿法的收敛阶数是多少？

如果 \(p\) 是 \(f\) 中的一个根，且重数 (multiplicity) 为 \(m\)，那么 \(f(x) = (x - p)^m q(x)\) 且 \(q(p) \ne 0\)。

根据牛顿法：\(p_n = g(p_{n-1}) \text{ for } n \ge 1 \text{ with } g(x) = x - \dfrac{f(x)}{f'(x)}\)，得到：

\[ g'(p) = \Big|1 - \dfrac{f'(p)^2 - f(p)f''(p)}{f'(p)^2}\Big| = 1 - \dfrac{1}{m} < 1 \]

所以此时牛顿法收敛，但不是二次收敛。

幸运的是，存在一种可以加快收敛速度的方法：将有重根的 \(f\) 转换为等价的另一个有简单根的函数，在这个新的函数上使用牛顿法。具体来说：

  • 令 \(\mu(x) = \dfrac{f(x)}{f'(x)}\)，那么 \(f\) 的重根 = \(\mu\) 的简单根

  • 在 \(\mu\) 上应用牛顿法：

    \[ g(x) = x - \dfrac{\mu(x)}{\mu'(x)} = x - \dfrac{f(x)f'(x)}{[f'(x)]^2 - f(x)f''(x)} \]

对上述方法的评价

  • 优点：二次收敛
  • 缺点：
    • 需要额外计算 \(f''(x)\)
    • 分母是两个都接近于 0 的数的差

Accelerating Convergence⚓︎

Aitken's \(\Delta^2\) Method⚓︎

第 5 页的 PPT 还没整理。

定义

对于给定的序列 \(\{p_n\} (n = 1, 2, \dots)\)，前向差(forward difference) \(\Delta p_n = p_{n+1} - p_n (n \ge 0)\)。更高次的幂 \(\Delta^k p_n\) 可以被递归定义为 \(\Delta^k p_n = \Delta (\Delta^{k-1} p_n) (k \ge 2)\)

Aitken's \(\Delta^2\) 法：\(\hat{p}_n = \{\Delta^2\}(p_n) = p_n - \dfrac{(\Delta p_n)^2}{\Delta^2 p_n} (n \ge 0)\)

定理

假设序列 \(\{p_n\} (n = 1, 2, \dots)\) 线性收敛到极限 \(p\)；且对于所有充分大的数 \(n\)，有 \((p_n - p)(p_{n+1} - p) > 0\)。那么序列 \(\{\hat{p}_n\} (n = 1, 2, \dots)\) 收敛到 \(p\) 的速度快于 \(\{p_n\} (n = 1, 2, \dots)\)，即：

\[ \lim\limits_{n \rightarrow \infty} \dfrac{\hat{p}_n - p}{p_n - p} = 0 \]

Steffensen's Method⚓︎

Steffensen 法：若 \(g'(p) \ne 1\)，那么可以做到局部二次收敛。

\[ \begin{align} p_0^{(0)}, p_1^{(0)} = g(p_0^{(0)}), p_2^{(0)} = g(p_2^{(0)}) \notag \\ p_0^{(1)} = \{\Delta^2\}(p_0^{(0)}), p_1^{(1)} = \{\Delta^2\}(p_0^{(1)}) , p_2^{(1)} = \{\Delta^2\}(p_1^{(1)})\notag \\ p_0^{(2)} = \{\Delta^2\}(p_0^{(1)}), \dots \notag \end{align} \]

评论区

如果大家有什么问题或想法，欢迎在下方留言~