Chap 4: Numerical Differentiation and Integration⚓︎

Numerical Differentiation⚓︎

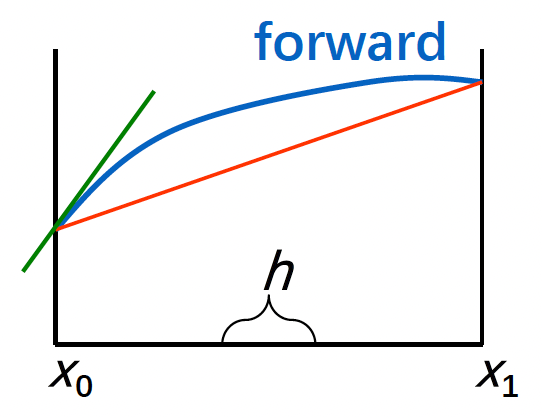
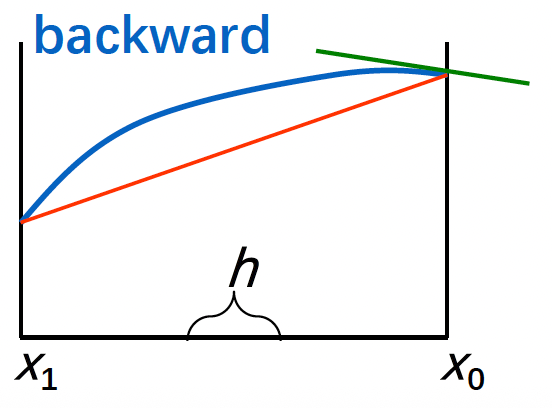
目标：对于给定的 \(x_0\)，近似计算 \(f'(x_0)\)（即数值微分(numerical differentiation)）

微分计算公式：\(f'(x_0) = \lim\limits_{h \rightarrow 0} \dfrac{f(x_0 + h) - f(x_0)}{h}\)

• 前向：\(f'(x_0) \approx \dfrac{f(x_0 + h) - f(x_0)}{h}\)
• 后向：\(f'(x_0) \approx \dfrac{f(x_0) - f(x_0 - h)}{h}\)

现在我们用 \(f(x)\) 的带有插值点 \(x_0, x_0 + h\) 的拉格朗日多项式来近似表示 \(f(x)\)：

因此 \(f'(x_0) = \dfrac{f(x_0 + h) - f(x_0)}{h} - \dfrac{h}{2}f''(\xi)\)

接下来用插值点为 \(\{x_0, x_1, \dots, x_n\}\) 的拉格朗日多项式来近似表示 \(f(x)\)

上述导数公式被称为近似 \(f'(x_j)\) 的 n+1 点公式((n+1)-point formula)。

例子

例 1 例 2

题目解答

给定三个点 \(x_0, x_0 + h, x_0 + 2h\)，请推到关于它们的三点公式，然后选出对于 \(f'(x)\) 而言最佳的三点公式。

根据前面的 n+1 点公式，不难得到：

\[ \begin{align} f'(x_j) = & f(x_0) \Big[ \dfrac{2x_j - x_1 - x_2}{(x_0 - x_1)(x_0 - x_2)} \Big] + f(x_1) \Big[ \dfrac{2x_j - x_0 - x_2}{(x_1 - x_0)(x_1 - x_2)} \Big] \notag \\ & + f(x_2) \Big[ \dfrac{2x_j - x_0 - x_1}{(x_2 - x_0)(x_2 - x_1)} \Big] + \dfrac{1}{6}f^{(3)}(\xi_j) \prod_{\substack{k = 0 \\ k \ne j}}^2(x_j - x_k)\ (j = 0, 1, 2) \notag \end{align} \]

将 \(x_0, x_1 = x_0 + h, x_2 = x_0 + 2h\) 代入上述公式，得到以下公式：

\[ \begin{align} f'(x_0) & = \dfrac{1}{h}\Big[-\dfrac{3}{2} f(x_0) + 2f(x_0 + h) - \dfrac{1}{2}f(x_0 + 2h) \Big] + \dfrac{h^2}{3} f^{(3)}(\xi_0) \notag \\ f'(x_0 + h) & = \dfrac{1}{h} \Big[ -\dfrac{1}{2} f(x_0) + \dfrac{1}{2} f(x_0 + 2h) \Big] - \dfrac{h^2}{6} f^{(3)}(\xi_1) \notag \\ f'(x_0 + 2h) & = \dfrac{1}{h} \Big[ \dfrac{1}{2} f(x_0) - 2f(x_0 + h) + \dfrac{3}{2} f(x_0 + 2h) \Big] + \dfrac{h^2}{3} f^{(3)}(\xi_2) \notag \end{align} \]

方便起见，对于后两个公式，我们用 \(x_0\) 替代原来的 \(x_0 + h\) 和 \(x_0 + 2h\)，得到：

\[ \begin{align} f'(x_0) & = \dfrac{1}{h}\Big[-\dfrac{3}{2} f(x_0) + 2f(x_0 + h) - \dfrac{1}{2}f(x_0 + 2h) \Big] + \dfrac{h^2}{3} f^{(3)}(\xi_0) \notag \\ f'(x_0) & = \dfrac{1}{h} \Big[ -\dfrac{1}{2} f(x_0 - h) + \dfrac{1}{2} f(x_0 + h) \Big] - \dfrac{h^2}{6} f^{(3)}(\xi_1) \notag \\ f'(x_0 + 2h) & = \dfrac{1}{h} \Big[ \dfrac{1}{2} f(x_0 - 2h) - 2f(x_0 - h) + \dfrac{3}{2} f(x_0) \Big] + \dfrac{h^2}{3} f^{(3)}(\xi_2) \notag \end{align} \]

观察发现第 1 个和第 3 个式子唯一的区别仅在 \(h\) 和 \(-h\)，所以实际上只剩下 2 个式子，它们就是我们要找的三点公式：

\[ \begin{align} f'(x_0) & = \dfrac{1}{h}\Big[-\dfrac{3}{2} f(x_0) + 2f(x_0 + h) - \dfrac{1}{2}f(x_0 + 2h) \Big] + \dfrac{h^2}{3} f^{(3)}(\xi_0)\ \xi_0 \in [x_0, x_0 + 2h] \notag \\ f'(x_0) & = \dfrac{1}{h} \Big[ -\dfrac{1}{2} f(x_0 - h) + \dfrac{1}{2} f(x_0 + h) \Big] - \dfrac{h^2}{6} f^{(3)}(\xi_1)\ xi_1 \in [x_0 - h, x_0 + h] \notag \end{align} \]

题目解答

寻找近似计算 \(f''(x_0)\) 的方式。

考虑在 \(x_0\) 处的 \(f(x_0 + h), f(x_0 - h)\) 的泰勒展开式：

\[ \begin{align} f(x_0 + h) & = f(x_0) + f'(x_0) h + \dfrac{1}{2}f''(x_0)h^2 + \dfrac{1}{6} f'''(x_0) h^3 + \dfrac{1}{24} f^{(4)} (\xi_1) h^4 \notag \\ f(x_0 - h) & = f(x_0) - f'(x_0) h + \dfrac{1}{2}f''(x_0)h^2 - \dfrac{1}{6} f'''(x_0) h^3 + \dfrac{1}{24} f^{(4)} (\xi_{-1}) h^4 \notag \end{align} \]

因此：\(f''(x_0) = \dfrac{1}{h^2} [f(x_0 - h) - 2f(x_0) + f(x_0 + h)] - \dfrac{h^2}{12} f^{(4)} (\xi)\)

Elements of Numerical Integration⚓︎

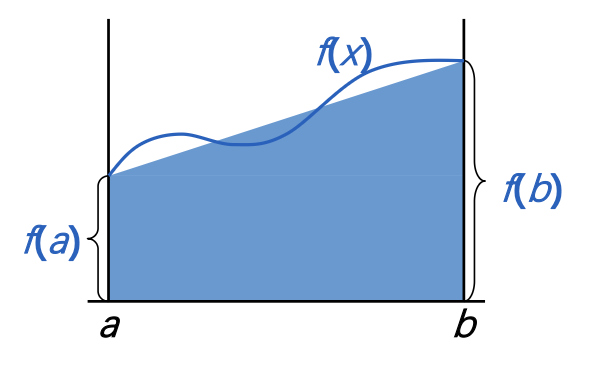
目标：近似计算 \(I = \int_a^b f(x) dx\)（即数值求积(numerical quadratrue)）

思路：使用 \(f(x)\) 的拉格朗日插值多项式——从区间 \([a, b]\) 上选择一组不同的点 \(a \le x_0 < x_1 \dots < x_n \le b\)。拉格朗日多项式为 \(P_n(x) = \sum\limits_{k=0}^n f(x_k) L_k(x)\)，因此：

令 \(A_k = \int_a^b L_k(x) dx = \int_a^b \prod\limits_{j \ne k} \dfrac{x - x_j}{x_k - x_j} dx\)

误差 \(R[f]\) 为：

例子

题目解答

考虑在 \([a, b]\) 上的线性插值，我们有 \(P_1(x) = \dfrac{x - b}{a - b}f(a) + \dfrac{x - a}{b - a}f(b)\)。可以得到：

• \(A_1 = A_2 = \dfrac{b - a}{2}\)
• \(\int_a^b f(x) dx \approx \dfrac{b - a}{2}[f(a) + f(b)]\)

请计算上述公式的精度。

考虑 \(x^k(k = 0, 1, \dots)\)：

• \(x^0\)：\(\int_a^b 1dx = b - a = \dfrac{b - a}{2}[1 + 1]\)
• \(x^1\)：\(\int_a^b xdx = \dfrac{b^2 - a^2}{2} = \dfrac{b - a}{2}[a + b]\)
• \(x^2\)：\(\int_a^b x^2dx = \dfrac{b^3 - a^3}{3} \ne \dfrac{b - a}{2}[a^2 + b^2]\)

因此精度阶数 = 1

对于等间距的节点 \(x_i = a + ih, h = \dfrac{b - a}{n}, i = 0, 1, \dots, n\)

其中标绿色的部分（\(\dfrac{(-1)^{n-i}}{ni!(n - i)!} \int_0^n \prod\limits_{i \ne j} (t - j) dt\)）被称为科茨系数(Cotes cofficient)，记作 \(C_i^{(n)}\)

• \(n = 1\)
  • \(C_0^{(1)} = C_1^{(1)} = \dfrac{1}{2}\)
  • \(\int_a^b f(x) dx \approx \dfrac{b - a}{2}[f(a) + f(b)]\)（称为梯形法则(trapezoidal rule)）
  • \(R[f] = \int_a^b \dfrac{f''(\xi_x)}{2!}(x-a)(x-b) dx = -\dfrac{1}{12}h^3f''(\xi)\)
  • \(\xi \in [a, b], h = \dfrac{b - a}{1}\)
  • 精度 = 1
• \(n = 2\)
  • \(C_0^{(2)} = \dfrac{1}{6}, C_1^{(2)} = \dfrac{2}{3}, C_2^{(2)} = \dfrac{1}{6}\)
  • \(\int_a^b f(x) dx \approx \dfrac{b - a}{6}[f(a) + 4f(\dfrac{a+b}{2}) + f(b)]\)（称为辛普森法则(Simpson's rule)）
  • \(R[f] = -\dfrac{1}{90} h^5 f^{(4)}(\xi)\)
  • \(\xi \in (a, b), h = \dfrac{b - a}{2}\)
  • 精度 = 3
• \(n = 3\)：辛普森 3/8 法则，精度 = 3，\(R[f] = -\dfrac{3}{80}h^5 f^{(5)}(\xi)\)
• \(n = 4\)：科茨法则(Cotes' Rule)，精度 = 5，3，\(R[f] = -\dfrac{8}{945}h^7 f^{(6)}(\xi)\)

Compotsite Numerical Integration⚓︎

由于高阶多项式容易发生振荡，所以我们用分段(piecewise) 插值的方式来近似 \(f(x)\)。这里用到了低阶的牛顿 - 科茨公式。

Composite Trapezoidal Rule⚓︎

复合梯形法则(composite trapezoidal rule) 涉及到的变量有：\(h = \dfrac{b-a}{n}, x_k = a + kh\ (k=0, \dots, n)\)。

我们将梯形公式作用在每个区间 \([x_{k-1}, x_k]\) 上，即：

\(R[f]\) 的公式涉及到中值定理(MVT)。

Composite Simpson's Rule⚓︎

复合辛普森法则(composite Simpson rule) 涉及到的变量和复合梯形公式一致：\(h = \dfrac{b-a}{n}, x_k = a + kh\ (k=0, \dots, n)\)。

我们将辛普森公式作用在每个区间 \([x_{k-1}, x_k]\) 上，即：

上述的复合方法都是稳定的。来看下面这个例子：

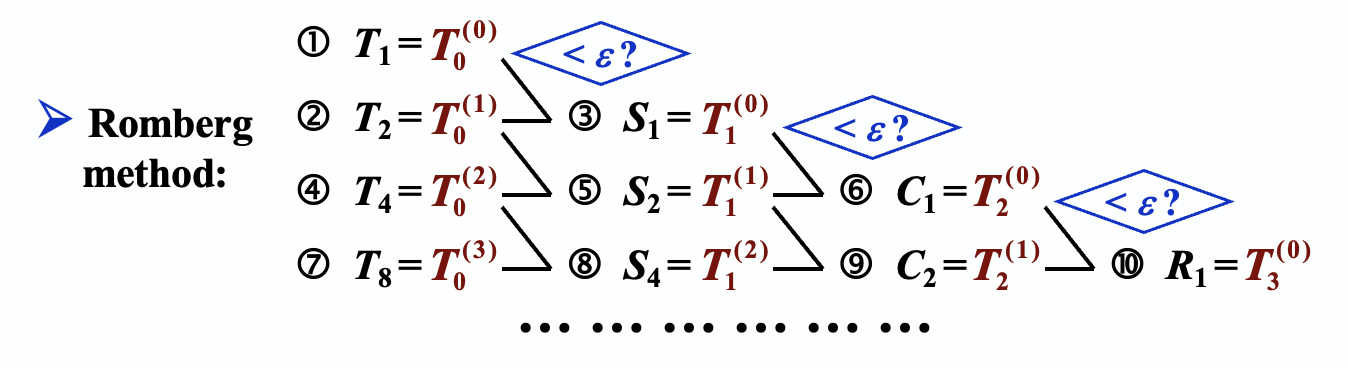
Romberg Integration⚓︎

回顾一下梯形法则的误差公式：\(R_n[f] = -\dfrac{h^2}{12}(b-a)f''(\xi)\)。当我们将每个子区间的长度缩减至原来的一半时，

从而得到：\(\dfrac{I - T_{2n}}{I - T_n} \approx \dfrac{1}{4}\)，解得 \(I \approx \dfrac{4T_{2n} - T_n}{4 - 1} = \dfrac{4}{3}T_{2n} - \dfrac{1}{3}T_n = S_n\)

一般情况下：

• \(\dfrac{4T_{2n} - T_n}{4 - 1} = S_n\)
• \(\dfrac{4^2S_{2n} - S_n}{4^2 - 1} = C_n\)
• \(\dfrac{4^3C_{2n} - C_n}{4^3 - 1} = R_n\) -> Romberg 序列(Romberg sequence)

Romberg 法如下所示：

可以看到，Romberg 法通过不断将积分区间对分（涉及到接下来介绍的 Richardson 外推法），在这些子区间上作用（复合）梯形法则，从而提高积分精度。

其递推公式为：

对应的表格为：

Step 1  Set h = b - a;
            R[1][1] = h / 2 * (f(a) + f(b));
Step 2  Output(R[1][1]);
Step 3  for i = 2, ..., n do steps 4-8:
    // approximation from Trapezoidal method
    Step 4  Set R[2][1] = 1/2 * [R[1][1] + h * sum(k=1, pow(2, i-2), f(a + (k - 0.5) * h))];
    Step 5  for j = 2, ..., i:
                // extrapolation
                set R[2][j] = R[2][j-1] + (R[2][j-1] - R[1][j-1]) / (pow(4, j-1) - 1);
    Step 6  Output(R[2][j] for j = 1, 2, ..., i);
    Step 7  Set h /= 2;
    Step 8  for j = 1, 2, ..., i set R[1][j] = R[2][j];    // update row 1 of R
Step 9  STOP.

Richardson's Extrapolation⚓︎

Richardson 外推法(Richardson's extrapolation) 实现的目标是：使用低阶公式获取高精度的结果。

它的核心思想是：利用同一数值方法在不同步长下计算出的结果，通过线性组合来消除或减小近似解中的主要误差项，从而得到一个更高精度的估计值。

这和求解一元方程的 Aitken's \(\Delta^2\) 法在思想上有共通之处。

假设对于某些 \(h \ne 0\)，我们有公式 \(T_0(h)\)，用于近似未知量 \(I\)，并且其截断误差的形式为：

用 \(h\) 一半的值替代自身，我们有：

结合上述两个公式，我们就可以将精度从 \(O(h)\) 提升至 \(O(h^2)\)：

令 \(T_1 = \dfrac{2T_0(\frac{h}{2}) - T_0(h)}{2 - 1} = I + \beta_1 h^2 + \beta_2 h^3 + \dots\)。类似地，我们可以将精度提升至 \(O(h^3)\)：

以此类推，我们可以将精度可以提升到 \(m+1\) 阶：

例子

题目解答

由 Gemini 2.5 pro 作答，且通过笔者验证。

1. 建立误差方程：

   令 \(N(A) = \frac{f(x_0+A)-2f(x_0)+f(x_0-A)}{A^2}\)。我们可以将真实值表示为：

   \[f''(x_0) = N(A) + K_1A^2 + K_2A^4 + \dots\]

   其中 \(K_1 = -\frac{f^{(4)}(x_0)}{12}\)。

2. 使用两种步长：

   我们使用步长 \(A\) 和 \(A/2\) 来计算近似值：

   • 步长 A: \(f''(x_0) = N(A) + K_1A^2 + K_2A^4 + \dots\)（式 1）
   • 步长 A/2: \(f''(x_0) = N(A/2) + K_1(A/2)^2 + K_2(A/2)^4 + \dots = N(A/2) + \frac{K_1}{4}A^2 + \frac{K_2}{16}A^4 + \dots\)（式 2）

3. 消除 \(O(A^2)\) 误差项：

   为了消除 \(K_1A^2\) 项，我们将（式 2）乘以 4，然后减去（式 1）：

   • \(4f''(x_0) = 4N(A/2) + K_1A^2 + \frac{K_2}{4}A^4 + \dots\)
   • \(f''(x_0) = N(A) + K_1A^2 + K_2A^4 + \dots\)

   两式相减得到：

   \(3f''(x_0) = 4N(A/2) - N(A) - \frac{3K_2}{4}A^4 + \dots\)

4. 导出新公式：

   整理上式，我们得到一个新的 \(f''(x_0)\) 的近似公式，其误差项为 \(O(A^4)\)：

   \[f''(x_0) \approx \frac{4N(A/2) - N(A)}{3}\]

   这个公式的误差为 \(O(A^4)\)，比原来的 \(O(A^2)\) 精度更高。

Adapative Quadrature Methods⚓︎

目标：预测函数变化量，根据变化的需求调整步幅。

前面介绍的复合积分方法的缺点是：对所有区间递归划分子区间，这样计算量太大，而且还有产生了许多不必要的计算，这很浪费。因此，我们采用一种仅对具有较大误差(large error) 的区间进行划分的方法，避免额外的计算。我们称这样的方法为自适应求积方法(adapative quadrature mehtods)。

那么什么算“较大误差”呢？一种简单的确定策略是使用 \(\int_a^b f(x) dx\) 的总误差 \(\varepsilon\) 来确定边界：在长度为 \(h\) 的区间中，误差应该要小于 \(h \dfrac{\varepsilon}{b - a}\)。当误差超过这个值时，我们就认为是较大误差，需要继续划分该区间。

接下来的问题就是如何估计一个区间的误差。这里我们暂时仅考虑辛普森法则下的误差估计——即如何估计：

其中 \(h = \dfrac{b-a}{2}, \xi \in [a, b]\)。

这个问题的答案在例 2 中给出。

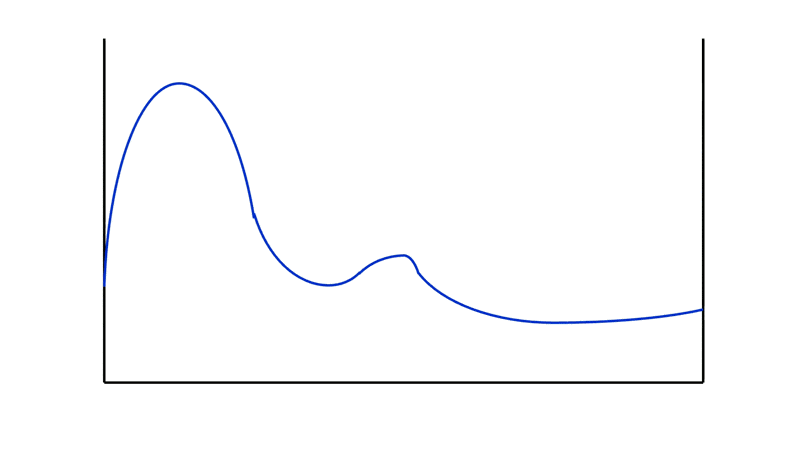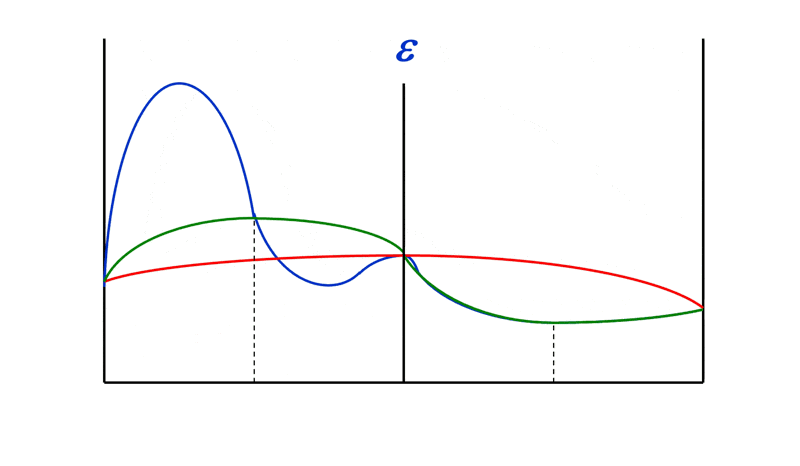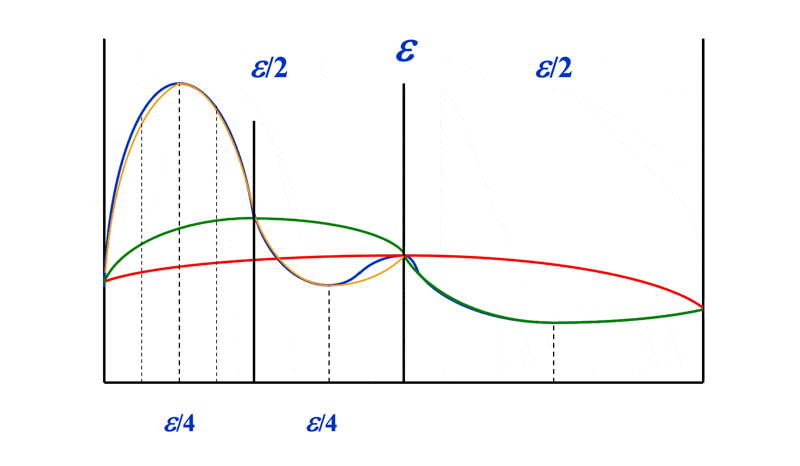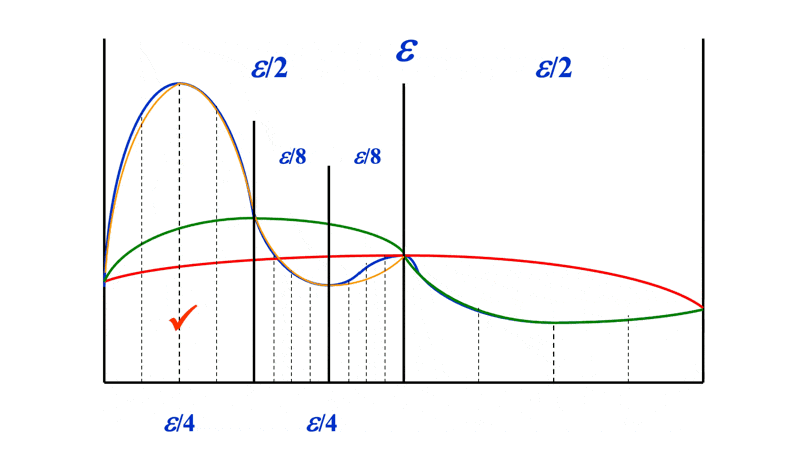
例子

例 1 例 2

动画演示

考虑基于复合辛普森法则的自适应方法：

\[ \int_a^b f(x)dx = S(a, b) - \dfrac{h^5}{90}f^{(4)}(\xi) \]

其中 \(S(a, b) = \dfrac{h}{3}[f(a) + 4f(a + h) + f(b)], h = \dfrac{b-a}{2}\)。令：

\[ \begin{align} S\Big(a, \dfrac{a+b}{2}\Big) = \dfrac{h}{6}[f(a) + 4f(a + h/2) + f(a + h)] \notag \\ S\Big(\dfrac{a+b}{2}, b\Big) = \dfrac{h}{6}[f(a + h) + 4f(a + 3h/2) + f(b)] \notag \end{align} \]

那么：

\[ \int_a^b f(x) dx = S\Big(a, \dfrac{a+b}{2}\Big) + S\Big(\dfrac{a+b}{2}, b\Big) - \dfrac{1}{16} \times \dfrac{h^5}{90}f^{(4)}(\eta) \\ \begin{align} &\ \Big| \int_a^b f(x) dx - S\Big(a, \dfrac{a+b}{2}\Big) - S\Big(\dfrac{a+b}{2}, b\Big) \Big| \notag \\ \approx &\ \dfrac{1}{15} \Big|S(a, b) - S\Big(a, \dfrac{a+b}{2}\Big) - S\Big(\dfrac{a+b}{2}, b\Big) \Big| \notag \\ < &\ \varepsilon \notag \end{align} \]

可以看到，相比一般的辛普森法则，结合自适应方法后误差只有原来的 \(\dfrac{1}{15}\) 🎉

Gaussian Quadrature⚓︎

目标：构造一个公式 \(\int_a^b w(x) f(x) dx \approx \sum\limits_{k=0}^n A_k f(x_k)\)，对于 \(n+1\) 个点而言精度为 \(2n+1\)。

思路：确定 \(2n+2\) 个未知量 \(x_0, \dots, x_n;\ A_0, \dots, A_n\)，使得公式在 \(f(x) = 1, x, x^2, \dots, x^{2n+1}\) 上都是精确的。点 \(x_0, \dots, x_n\) 被称为高斯点(Gaussian points)，这个方法被称为高斯求积(Gaussian quadrature)

正交多项式的集合 \(\{\varphi_0, \varphi_1, \dots, \varphi_n, \dots\}\) 是线性独立的，且 \(\varphi_{n+1}\) 和任何多项式 \(P_m(x)\ (m \le n)\) 正交。所以，如果我们拿 \(\varphi_{n+1}\) 作为 \(W(x)\)，那么 \(\varphi_{n+1}\) 的根就是高斯点了。

一些特殊的正交多项式：

• 勒让德多项式(Legendre polynomials)：定义在 \([-1, 1]\) 上且 \(w(x) \equiv 1\)

  \[ P_k(x) = \dfrac{1}{2^k k!} \dfrac{d^k}{dx^k}(x^2 - 1)^k \quad \quad (P_k, P_l) = \begin{cases}0 & k \ne l \\ \dfrac{2}{2k+1} & k = l\end{cases} \]

  \(P_0 = 1, P_1 = x, (k + 1)P_{k+1} = (2k + 1)xP_k - kP_{k-1}\)

  使用 \(P_{n+1}\) 的根的公式称为高斯 - 勒让德求积公式。

• 切比雪夫多项式(Chebyshev polynomials)：定义在 \([-1, 1]\) 上且 \(w(x) = \dfrac{1}{\sqrt{1 - x^2}}\)

  \[ T_k(x) = \cos (k \times \arccos x) \]

  \(T_{n+1}\) 的根为 \(x_k = \cos \Big(\dfrac{2k + 1}{2n + 2} \pi \Big) \quad (k = 0, \dots, n)\)

  公式 \(\int_{-1}^1 \dfrac{1}{\sqrt{1 - x^2}} f(x) dx = \sum\limits_{k=0}^n A_k f(x_k)\) 称为高斯 - 切比雪夫求积公式。

  • 注意到积分端点 \(\pm 1\) 是积分上的奇点(singular points)，此时在等间距的点上使用牛顿 - 科茨公式会出现问题；而高斯积分能够避免这个问题。

对应的作业练习📝

对应小测 11、12💯