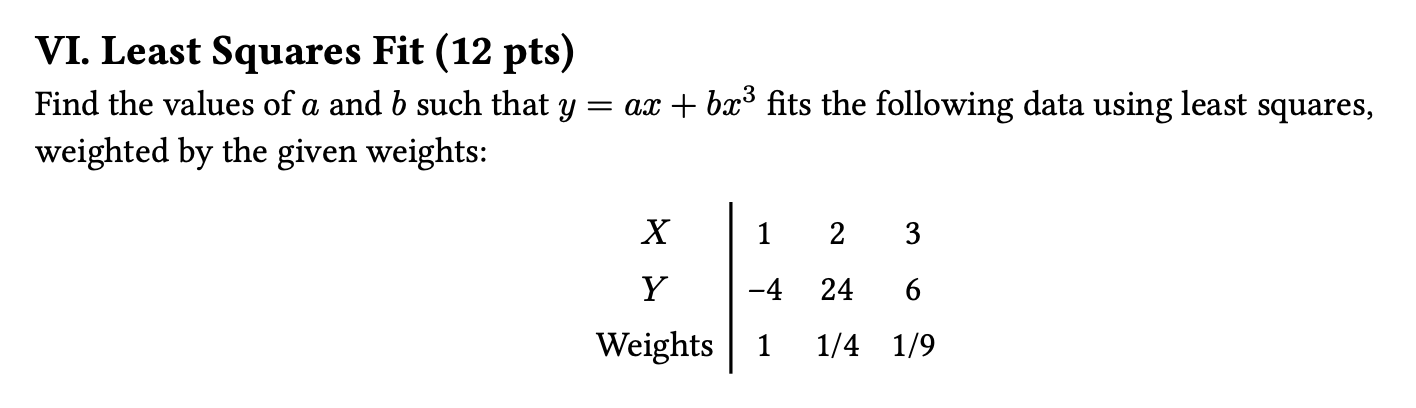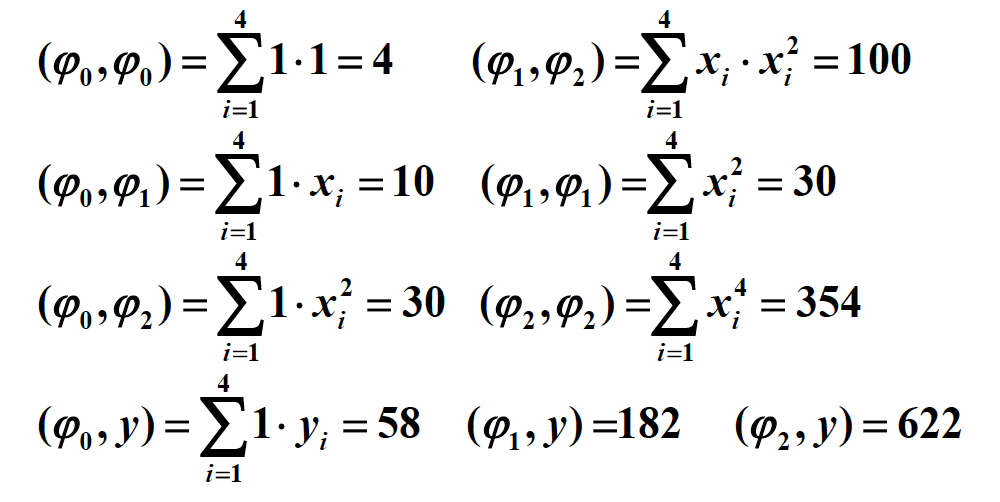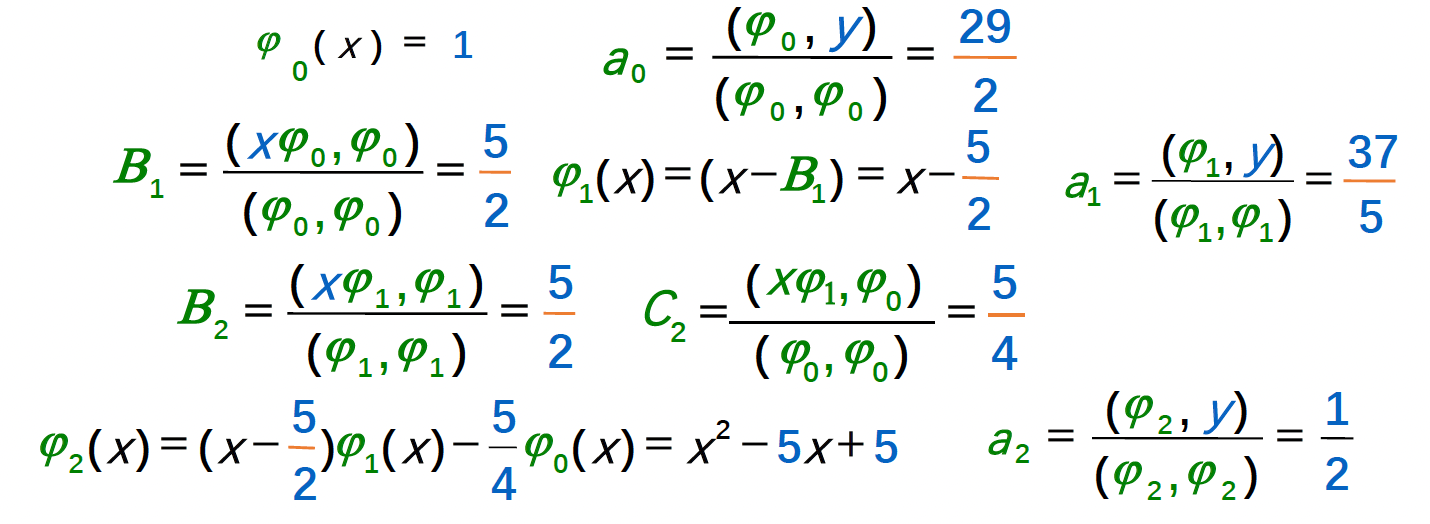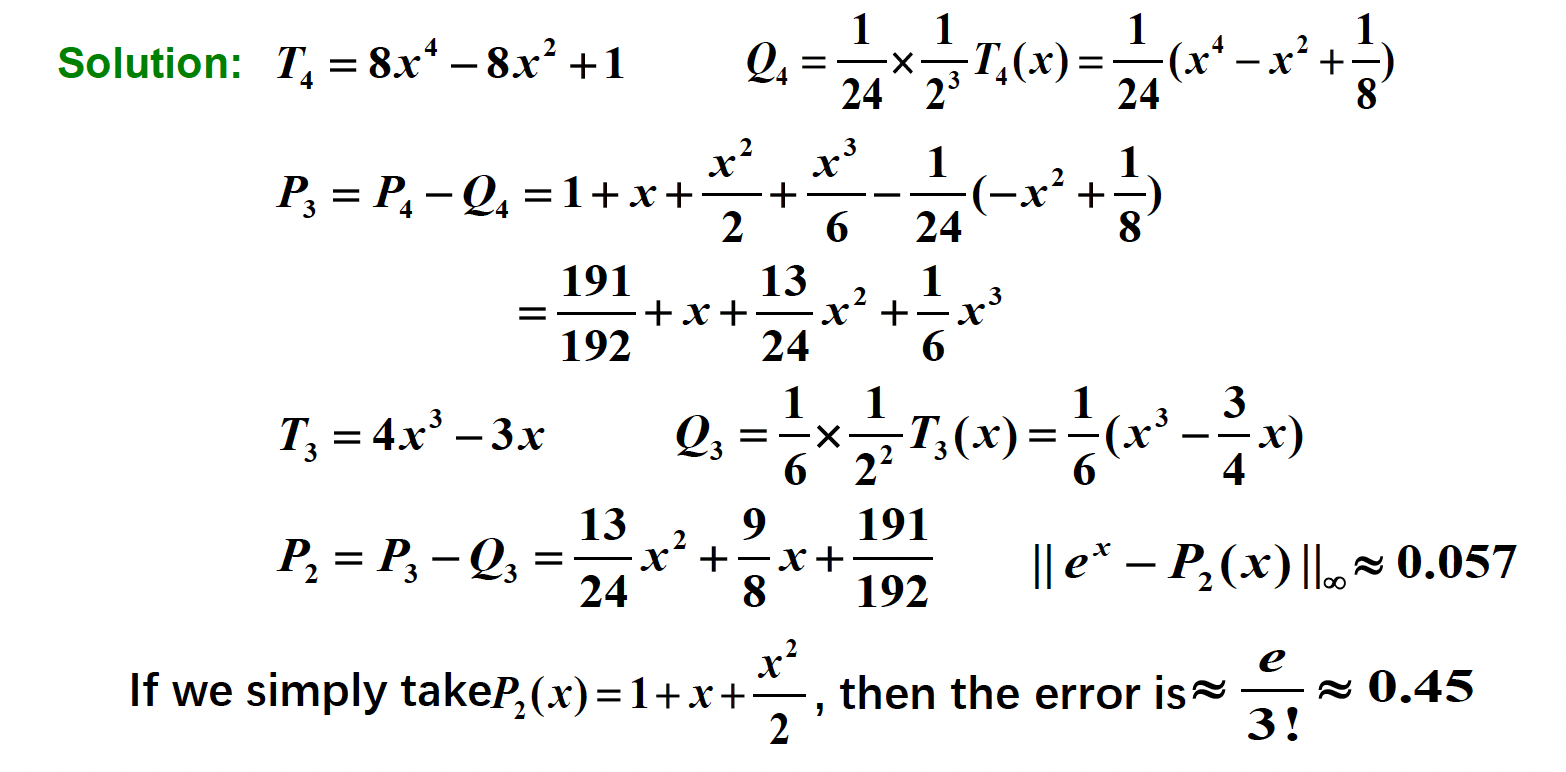Chap 8: Approximation Theory⚓︎

近似理论的目标是：给定 \(x_1, \dots, x_m\) 和 \(y_1, \dots y_m\)，寻找更简单的函数 \(P(x) \approx f(x)\)（近似表示 \(f(x)\)）。

然而，因为有时 \(m\) 可能会特别大，并且 \(y_i\) 是不准确的实验数据（即 \(y_i \ne f(x_i)\)），所以此时更合理的做法是去寻找最佳拟合的 \(P(x)\)，使得对于所有点而言，\(P(x_i) - y_i\) 尽可能小。下面我们就来介绍这些数学方法。

Discrete Least Square Approximation⚓︎

目标：确定一个多项式 \(P_n(x) = a_0 + a_1 x + \dots a_n x^n\)，用于近似表示一组数据 \(\{(x_i, y_i)\ |\ i = 1, 2, \dots, m\}\)，使得最小二乘误差 \(E_2 = \sum\limits_{i=1}^m [P_N(x_i) - y_i]^2\) 最小化，其中 \(n \ll m\)

关键：\(E_2\) 实际上是一个关于 \(a_0, a_1, \dots, a_n\) 的函数，也就是说 \(E_2(a_0, a_1, \dots, a_n) = \sum\limits_{i=1}^m [a_0 + a_1 x_i + \dots + a_n x_i^n - y_i]^2\)。要想让 \(E_2\) 最小化，必要条件是 \(\dfrac{\partial E_2}{\partial a_k} = 0, k = 0, \dots, n\)

令 \(b_k = \sum\limits_{i=1}^m x_i^k, c_k = \sum\limits_{i=1}^m y_i x_i^k\)，那么：

例子

例 1 例 2

题目解答

法 1 法 2

令 \(y \approx P(x) = \dfrac{x}{ax + b}\)，寻找 \(a, b\)，使得 \(E_2(a, b) = \sum\limits_{i=1}^m \Big(\dfrac{x_i}{ax_i + b} - y_i\Big)^2\) 最小化。

线性化(linearization)：令 \(Y = \dfrac{1}{y}, X = \dfrac{1}{x}\)，那么 \(Y \approx a + b X\) 就是一个线性问题了。

将 \((x_i, y_i)\) 转换为 \((X_i, Y_i)\)，\(a, b\) 就能被解出来了。

令 \(y \approx P(x) = ae^{-\frac{b}{x}}\)，不难发现 \(\ln y \approx \ln a - \dfrac{b}{x}\)

线性化：令 \(Y = \ln y, X = \dfrac{1}{x}, A = \ln a, B = -b\)，得到 \(Y \approx A + BX\) 这样一个线性问题。

将 \((x_i, y_i)\) 转换为 \((X_i, Y_i)\)，\(a, b\) 就能被解出来了（\(a = e^A, b = -B, P(x) = ae^{-\frac{b}{x}}\)）

题目解答

• 拿那个带权重的 LSA 公式计算，得到一个关于 \(a, b\) 的函数
• 当所有偏导数均为 0 时，函数值最小；所以在代入具体值前，建议先化简偏导数公式，以减小计算量
• 得到的偏导数为：\(\begin{cases}\dfrac{\partial S}{\partial a} = 0 \Rightarrow \sum w_i x_i y_i = 0 \\ \dfrac{\partial S}{\partial b} = 0 \Rightarrow \sum w_i x_i^3 y_i = 0\end{cases}\)
• 再代入具体值，就可以得到关于 \(a, b\) 的二元一次方程
• 解得 \(a = \dfrac{8}{7}, b = \dfrac{23}{49}\)

Orthorgonal Polynomials and Least Squares Approximation⚓︎

目标：

• 离散版本：给定 \(x_1, \dots, x_m;\ y_1, \dots, y_m\)，找到更简单的函数 \(P(x) \approx f(x)\)，使得 \(E = \sum\limits_{i=1}^m |P(x_i) - y_i|^2\) 最小化。
• 连续版本：给定在 \([a, b]\) 上的函数 \(f(x)\)，找到更简单的函数 \(P(x) \approx f(x)\)，使得 \(E = \int_a^b [P(x) - f(x)]^2 dx\) 最小化。

一些特殊的多项式：

• \(\{\varphi_j(x) = \cos jx\}, \{\psi_j(x) = \sin jx\} \Rightarrow \{\varphi_j(x), \psi_j(x)\}\) 得到的是三角多项式(trigonometric polynomial)
• \(\{\varphi_j(x) = e^{kjx}, k_i \ne k_j\}\) 得到的是指数多项式(exponential polynomial)

对于 \((f, g) = \begin{cases}\sum\limits_{i=1}^m w_i f(x_i) g(x_i) & \text{discrete version} \\ \int_a^b w(x) f(x) g(x) dx & \text{continuous version} \end{cases}\)，可以证明它表示的是一个内积(inner product)，且 \(\|f\| = \sqrt{(f, f)}\) 是一个范数。并且当 \((f, g) = 0\) 时，我们称 \(f, g\) 是正交的(orthogonal)。

因此一般的最小二乘近似问题可以被转换为：

令 \(P(x) = a_0 \varphi_0(x) + a_1 \varphi_1(x) + \dots + a_n \varphi_n(x)\)，然后与求解离散问题类似：\(\dfrac{\partial E}{\partial a_k} = 0\)，即对于所有 \(a_k\) 偏导数为 0 时误差取最小值。将等号左侧公式化简，可以得到：\(\sum\limits_{j=0}^n (\varphi_k, \varphi_j) a_j = (\varphi_k, f), k = 0, \dots, n\)，也就是说：

例子

题目解答

使用 \(y = a_0 + a_1 x + a_2 x^2\ (w \equiv 1)\) 近似点集 \(\{(1, 4), (2, 10), (3, 18), (4, 26)\}\)

\(\varphi_0(x) = 1, \varphi_1(x) = x, \varphi_2(x) = x^2\)，可以计算出：

\(\|B\|_{\infty} = 484, \|B^{-1}\|_{\infty} = \dfrac{63}{4} \Rightarrow K(B) = 7623\)

下面考虑构造正交多项式(orthogonal polynomials)。

例子

例 1 例 2

题目解答

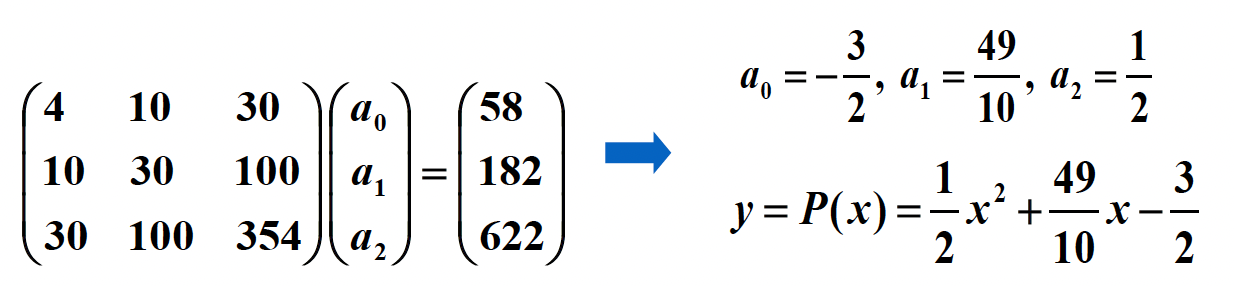
（和之前基本一样的）使用 \(y = c_0 + c_1 x + c_2 x^2, w \equiv 1\) 近似点集 \(\{(1, 4), (2, 10), (3, 18), (4, 26)\}\)

首先构造正交多项式 \(\varphi_0(x), \varphi_1(x), \varphi_2(x)\)，令 \(y = a_0 \varphi_0(x) + a_1 \varphi_1(x) + a_2 \varphi_2(x)\)（\(a_k = \dfrac{(\varphi_k, y)}{(\varphi_k, \varphi_k)}\)）。接下来就计算出这些值：

最终解得 \(y = \dfrac{1}{2}x^2 + \dfrac{49}{10}x - \dfrac{3}{2}\)

题目解答

知道内积的求解公式和上述正交多项式的构造后，这题其实挺容易的。所以就直接给出答案了：

• \(\varphi_0(x) = 1\)
• \(\varphi_1(x) = x - 2\)
• \(\varphi_2(x) = x^2 - 4x + \dfrac{8}{3}\)

Step 1  Set phi_0(x) ≡ 1; 
            a_0 = iprod(phi_0, y) / iprod(phi_0, phi_0); 
            P(x) = a_0 * phi_0(x); 
            err = iprod(y, y) - a_0 * iprod(phi_0, y);
Step 2  Set B_1 = iprod(x * phi_0, phi_0) / iprod(phi_0, phi_0); 
            phi_1(x) = x - B_1;
            a_1 = iprod(phi_1, y) / iprod(phi_1, phi_1); 
            P(x) += a_1 * phi_1(x); 
            err -= a_1 * iprod(phi_1, y);
Step 3  Set k = 1;
Step 4  while ((k < Max_n) && (|err| >= TOL)) do steps 5-7:
    Step 5  k++;
    Step 6  B_k = iprod(x * phi_1, phi_1) / iprod(phi_1, phi_1); 
            C_k = iprod(x * phi_1, phi_0) / iprod(phi_0, phi_0);
            phi_2(x) = (x - B_k) * phi_1(x) - C_k * phi_0(x); 
            a_k = iprod(phi_2, y) / iprod(phi_2, phi_2);
    Step 7  Set phi_0(x) = phi_1(x); phi_1(x) = phi_2(x);
Step 8  Output(); STOP.

Chebyshev Polynomials and Economization of Power Series⚓︎

前面讲过，解决一般的最小二乘近似问题的目标是：

再次明确：我们的目标是最小化 \(\|P - y\|_{\infty}\)——这是一个极小化极大问题(minimax problem)。

Targets⚓︎

目标 1.0：找到 \(n\) 阶多项式 \(P_n(x)\) 使得 \(\|P_n - f\|_{\infty}\) 最小化。

从任意地方构造出多项式并不容易，但我们能够检验多项式的一些特征：

• 如果 \(f \in C[a, b]\) 且 \(f\) 不是一个 \(n\) 阶多项式，那么存在一个唯一的多项式 \(P_n(x)\)，使得 \(\|P_n - f\|_{\infty}\) 最小化
• \(P_n(x)\) 存在，且必须同时有正负偏差点

• 切比雪夫定理(Chebyshev Theorem)：\(P_n(x)\) 最小化 \(\|P_n - f\|_{\infty}\ \Leftrightarrow P_n(x)\) 至少有 \(n+2\) 个关于 \(f\) 的正负偏差点。也就是说，存在一组点 \(a \le t_1 < \dots < t_{n+2} \le b\) 使得 \(P_n(t_k) - f(t_k) = \pm(-1)^k \|P_n - f\|_{\infty}\)。集合 \(\{t_k\}\) 被称为切比雪夫交替序列(Chebyshev alternating sequence)。

  \(P_n(x) - f(x)\) 至少有 \(n+1\) 个根。

  

目标 2.0：确定插值点 \(\{x_0, \dots, x_n\}\) 使得 \(P_n(x)\) 最小化余项 \(|P_n(x) - f(x)| = |R_n(x)| = \Big|\dfrac{f^{(n+1)}(\xi)}{(n+1)!} \prod\limits_{i=0}^n (x - x_i)\Big|\)

目标 2.1：找到 \(\{x_1, \dots, x_n\}\) 使得 \(\|w_n\|_{\infty}\) 在 \([-1, 1]\) 最小化，其中 \(w_n(x) = \prod\limits_{i=1}^n (x - x_i)\)

注意到 \(w_n(x) = x^n - P_{n-1}(x)\)，问题就变成了：

目标 3.0：找到多项式 \(P_{n-1}(x)\)，使得 \(\|x^n - P_{n-1}(x)\|_{\infty}\) 在 \([-1, 1]\) 上最小。

根据切比雪夫定理，我们知道 \(P_{n-1}(x)\) 有 \(n+1\) 个关于 \(x^n\) 的偏差点，也就是说 \(w_n(x)\) 在 \(n+1\) 个点上交替获得最大值和最小值。

Chebyshev Polynomials⚓︎

考虑 \(\cos (n \theta)\) 在 \([0, \pi]\) 上的 \(n+1\) 个极值。

令 \(x = \cos (\theta)\)，那么 \(x \in [-1, 1]\)。我们称 \(T_n(x) = \cos (n\theta) = \cos (n \cdot \text{arc} \cos x)\) 为切比雪夫多项式(Chebyshev polonomial)。

• \(T_n(x)\) 假设在 \(t_k = \cos \Big(\dfrac{k}{n} \pi\Big) (k = 0, 1, \dots, n)\) 上，在最大值 1 和最小值 -1 之间交替变换，也就是说 \(T_n(t_k) = (-1)^k \|T_n(x)\|_{\infty}\)
• \(T_n(x)\) 有 \(n\) 个根 \(x_k = \cos \Big(\dfrac{2k - 1}{2n} \pi \Big)(k = 1, \dots, n)\)
• \(T_n(x)\) 有递推关系式：\(T_0(x) = 1, T_1(x) = x, T_{n+1}(x) = 2x T_n(x) - T_{n-1}(x)\)
  • \(T_n(x)\) 是一个最高阶系数为 \(2^{n-1}\) 的 \(n\) 阶多项式
• \(\{T_0(x), T_1(x), \dots\}\) 在 \([-1, 1]\) 上关于权重函数 \(w(x) = \dfrac{1}{\sqrt{1 - x^2}}\) 上正交，也就是说 \((T_n, T_m) = \int_{-1}^1 \dfrac{T_n(x) T_m(x)}{\sqrt{1-x^2}} dx = \begin{cases}0 & n \ne m \\ \pi & n = m = 0 \\ \dfrac{\pi}{2} & n = m \ne 0\end{cases}\)

回到之前提到的目标：

• 目标 3.0：找到多项式 \(P_{n-1}(x)\)，使得 \(\|x^n - P_{n-1}(x)\|_{\infty}\) 在 \([-1, 1]\) 上最小。
  • 此时 \(w_n(x) = x^n - P_{n-1}(x) = \dfrac{T_n(x)}{2^{n-1}}\)
• 目标 2.1：找到 \(\{x_1, \dots, x_n\}\) 使得 \(\|w_n\|_{\infty}\) 在 \([-1, 1]\) 最小化，其中 \(w_n(x) = \prod\limits_{i=1}^n (x - x_i)\)
  • 此时 \(\min\limits_{w_n \in \widetilde{\Pi}_n} \|w_n\|_{\infty} = \Big\|\dfrac{1}{2^{n-1}} T_n(x)\Big\|_{\infty} = \dfrac{1}{2^{n-1}}\)。其中：\(\widetilde{\Pi}_n\) 是 \(n\) 阶的首一多项式，\(\{x_1, \dots, x_n\}\) 是 \(T_n(x)\) 的 \(n\) 个根
• 目标 2.0：确定插值点 \(\{x_0, \dots, x_n\}\) 使得 \(P_n(x)\) 最小化余项 \(|P_n(x) - f(x)| = |R_n(x)| = \Big|\dfrac{f^{(n+1)}(\xi)}{(n+1)!} \prod\limits_{i=0}^n (x - x_i)\Big|\)
  • 取 \(T_{n+1}(x)\) 上的 \(n+1\) 个根作为插值点 \(\{x_0, \dots, x_n\}\)，然后关于 \(f(x)\) 的插值多项式 \(P_n(x)\) 假设绝对误差的最小上界为 \(\dfrac{M}{2^n (n+1)!}\)

Economization of Power Series⚓︎

目标：给定 \(P_n(x) \approx f(x)\)，幂级数经济化(economization) 的目标是在确保精度损失最小的情况下，降低多项式的次数。

考虑一个任意的 \(n\) 阶多项式 \(P_n(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0\)，对应的多项式 \(P_{n-1}(x)\) 通过移除 \(n\) 阶多项式 \(Q_n(x)\)（\(x^n\) 项的系数为 \(a_n\)）得到。那么 \(\max\limits_{[-1, 1]} |f(x) - P_{n-1}(x)| \le \max\limits_{[-1, 1]} |f(x) - P_n(x)| + \max\limits_{[-1, 1]} |Q_n(x)|\)，而 \(Q_n(x)\) 能够反映精度的损失。

为了最小化精度损失，\(Q_n(x)\) 必须为 \(a_n \times \dfrac{T_n(x)}{2^{n-1}}\)

例子

题目解答

已知 \(f(x) = e^x\) 在 \([-1, 1]\) 上的 4 阶泰勒多项式为 \(P_4 = 1 + x + \dfrac{x^2}{2} + \dfrac{x^3}{6} + \dfrac{x^4}{24}\)。它的截断误差的上界为 \(|R_4(x)| \le \dfrac{e}{5!} |x^5| \approx 0.023\)。请将这个近似多项式的次数降至 2。

对应的作业练习📝

对应小测 8、9、10💯