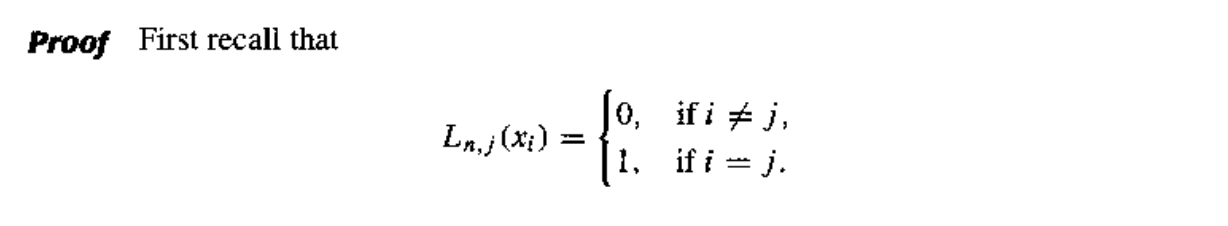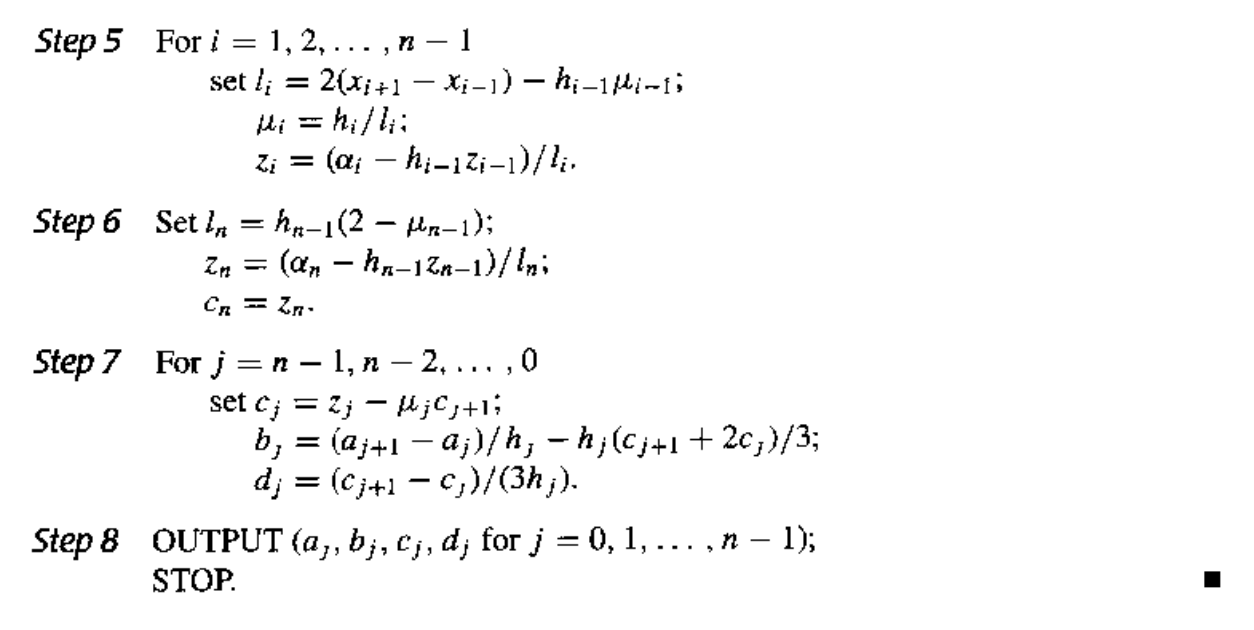Chap 3: Interpolation and Polynomial Approximation⚓︎

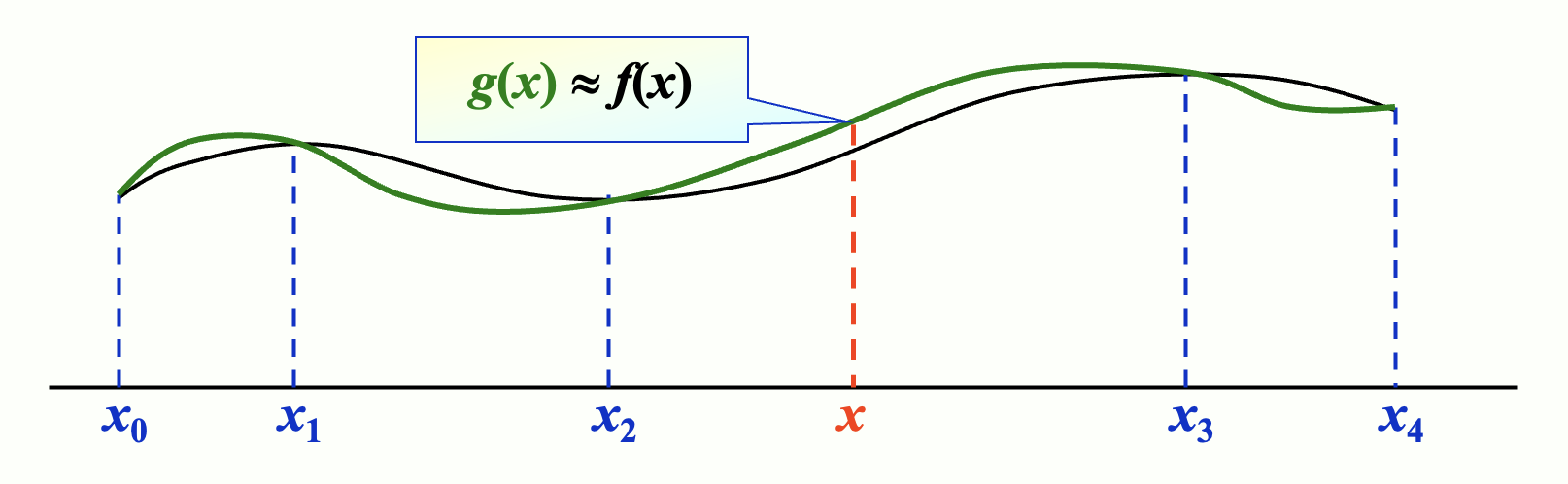
如果函数 \(y = f(x)\) 的计算过于复杂，或者甚至是未知的，一种近似求解的办法是：首先在一组点序列 \(x_0, \dots, x_n\) 上获取一组函数值 \(y_0 = f(x_0), \dots, y_n = f(x_n)\)，然后根据这些值构造一个相对简单的近似函数 \(g(x) \approx f(x)\)。

如果 \(g(x)\) 满足 \(\forall\ i = 0, \dots, n, g(x_i) = f(x_i)\)，我们称 \(g(x)\) 为 \(f(x)\) 的插值函数(interpolating function)。最常见的插值函数形式是代数多项式(algebraic polynomials)。

Interpolation and the Lagrange Polynomial⚓︎

目标：找到 \(n\) 阶多项式 \(P_n(x) = a_0 + a_1 x + \dots + a_n x^n\)，使得 \(\forall\ i = 0, \dots, n, P_n(x_i) = y_i\)。

注：对任何 \(i \ne j\)，必须满足 \(x_i \ne x_j\)

当 \(n = 1\) 时：给定 \(x_0, x_1; y_0, y_1\)。找到 \(P_1(x) = a_0 + a_1 x\)，使得 \(P_1(x_0) = y_0, P_1(x_1) = y_1\)。此时 \(P_1(x)\) 是一个经过给定两点 \((x_0, y_0), (x_1, y_1)\) 的线函数(line function)，即：

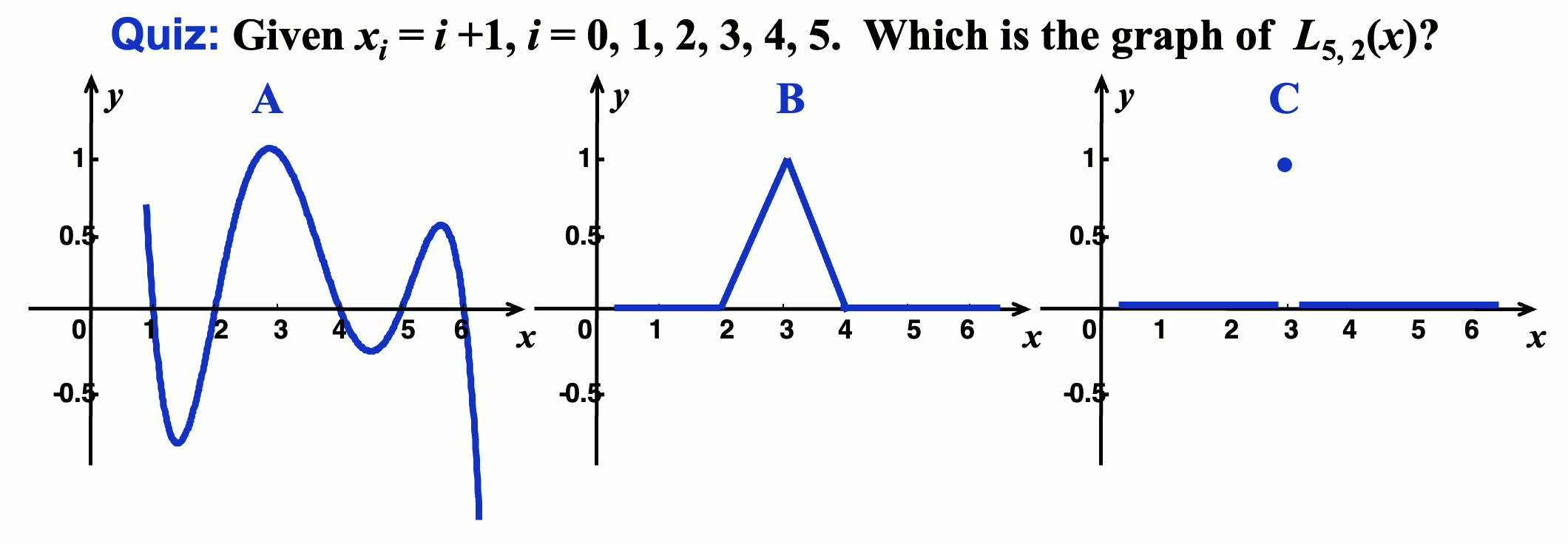
其中标红的项被称为拉格朗日基(Lagrange Basis)，它满足：\(L_{1, i}(x_j) = \delta_{ij} = \begin{cases}1 & \text{if } i = j \\ 0 & \text{if } i \ne j\end{cases}\)（称为 Kronecker 符号）

当 \(n \ge 1\) 时：我们要寻找 \(L_{n, i}(x)\ (i = 0, \dots, n)\)，使得 \(L_{n, i} (x_j) = \delta_{ij}\)。然后令 \(P_n(x) = \sum\limits_{i=0}^n L_{n, i}(x) y_i\)。因此 \(P_n(x_i) = y_i\)。

每个 \(L_{n, i}\) 都有 \(n\) 个根 \(x_0 \dots \widehat{x_i} \dots x_n\)。可以得到：

当 \(L_{n, i}(x_i) = 1\) 时，\(C_i = \prod\limits_{j \ne i} \dfrac{1}{x_i - x_j}\)

这里的 \(P_n(x)\) 就是n 阶拉格朗日插值多项式(n-th Lagrange interpolating polynomial)。

Quiz

题目答案

A

• 首先，拉格朗日多项式一定是个连续函数 -> C❌
• 其次，从它的式子就可以看出，它不可能是直线（\(n=5\) 表明它是六次曲线）-> B❌

下面我们来分析余项(remainder)：假如 \(a \le x_0 < x_1 < \dots < x_n \le b\) 且 \(f \in C^{n+1} [a, b]\)。考虑截断误差 \(R_n(x) = f(x) - P_n(x)\)

\(R_n(x)\) 至少有 \(n + 1\) 个根 \(\Rightarrow R_n(x) = K(x) \prod\limits_{i=0}^n (x - x_i)\)

修正任何 \(x \ne x_i\ (i = 0, \dots, n)\)。定义为 \(t \in [a, b]\) 定义函数 \(g\) 为：

\(g(x)\) 有 \(n + 2\) 个不同的根 \(x_0, \dots, x_n, x\ \Rightarrow g^{(n+1)}(\xi_x) = 0, \xi_x \in (a, b)\)

因此 \(R(x) = \dfrac{f^{(n+1)}(\xi_x)}{(n+1)!} \prod\limits_{i=0}^n (x - x_i)\)

Neville's Method⚓︎

上述定理表明插值多项式可以递归生成。比如，它们可以以下表所示的方式，一行行地生成插值多项式：

上述过程被称为 Neville 法。但 \(P\) 的记号显得过于笨重（一堆下标表示参与到多项式中的插值点）。观察发现，只需要两个下标就行了——我们用新的记号 \(Q_{i, j}(x)\ (0 \le j \le i)\) 来表示阶数为 \(j\) 的，在 \((j+1)\) 个数 \(x_{i-j}, x_{i-j+1}, \dots, x_{i-1}, x_i\) 上的插值多项式，即：\(Q_{i, j} = P_{i-j, i-j+1, \dots, i-1, i}\)。那么上面的表格就可以转化为：

而上面定理给出的递推公式可以转化为：

观察发现，求上面表格某一项的值时，我们会用到其左侧和左上角的两个项。

Step 1  for i = 1, 2, ..., n:
            for j = 1, 2, ..., i:
                set Q[i][j] = ((x - x[i-j]) * Q[i][j-1] - (x - x[i]) * Q[i-1][j-1]) / (x[i] - x[i-j]);
Step 2  Output(Q);
        STOP;

Divided Difference⚓︎

Divided differences is a recursive division process. Given a sequence of data points \((x_0,y_0),\dots,(x_n,y_n)\), the method calculates the coefficients of the interpolation polynomial of these points in the Newton form. -- Wikipedia

• 1 阶差商：\(f[x_i, x_j] = \dfrac{f(x_i) - f(x_j)}{x_i - x_j} (i \ne j, x_i \ne x_j)\)
• 2 阶差商：\(f[x_i, x_j, x_k] = \dfrac{f[x_i, x_j] - f[x_j, x_k]}{x_i - x_k} (i \ne k, x_i \ne x_k)\)

• \(k+1\) 阶差商：

  \[ \begin{align} f[x_0, \dots, x_{k+1}] & = \dfrac{f[\textcolor{cornflowerblue}{x_0}, x_1, \dots, x_k] - f[x_1, \dots, x_k, \textcolor{cornflowerblue}{x_{k+1}}]}{\textcolor{cornflowerblue}{x_0 - x_{k+1}}} \notag \\ & = \dfrac{f[x_0, \dots, x_{k-1}, \textcolor{cornflowerblue}{x_k}] - f[x_0, \dots, x_{k-1}, \textcolor{cornflowerblue}{x_{k+1}}]}{\textcolor{cornflowerblue}{x_k - x_{k+1}}} \notag \end{align} \]

事实上，\(f[x_0, \dots, x_k] = \sum\limits_{i=0}^k \dfrac{f(x_i)}{\omega_{k+1}' (x_i)}\)，其中 \(\omega_{k+1}(x) = \prod\limits_{i=0}^k (x - x_i), \omega_{k+1}'(x_i) = \prod\limits_{\substack{j = 0 \\ j \ne i}}^k (x_i - x_j)\)。这个公式的要点在于：\(f[x_0, \dots, x_k]\) 的值和 \(x_0, \dots, x_k\) 的顺序无关。

Newton's Interpolation⚓︎

目标：得到 \(N_n(x) = a_0 + a_1(x - x_0) + a_2(x - x_0)(x - x_1) + \dots + a_n(x - x_0) \dots (x - x_{n-1})\)

我们将 1 阶差商、2 阶差商、...、\(k+1\) 阶差商展开，得到：

计算 \((1) + (x - x_0) \times (2) + \dots + (x - x_0) \dots (x - x_{n-1}) \times (n-1)\)，得到：

其中红色部分就是我们要求的 \(N_n(x)\) ，而绿色部分是 \(R_n(x)\)。所以，\(a_i = f[x_0, \dots, x_i]\)

Step 1  for i = 1, 2, ..., n:
            for j = 1, 2, ..., i:
                set F[i][j] = (F[i][j-1] - F[i-1][j-1]) / (x[i] - x[i-j]);
Step 2  Output(F[0][0], F[1][1], ..., F[n][n]);  // F[i][i] is f[x[0], x[1], ..., x[i]]
        STOP;

Formulae with Equal Spacing⚓︎

如果这些点是等间距的，即 \(x_i = x_0 + ih\ (i = 0, \dots, n)\)，那么：

• 前向差(forward difference)：\(\Delta f_i = f_{i+1} - f_i, \Delta^k f_i = \Delta(\Delta^{k-1} f_i) = \Delta^{k-1} f_{i+1} - \Delta^{k-1} f_i\)
• 后向差(backward difference)：：\(\nabla f_i = f_i - f_{i-1}, \nabla^k f_i = \nabla(\nabla^{k-1} f_i) = \nabla^{k-1} f_i - \nabla^{k-1} f_{i-1}\)
• 中心差(centered difference)：\(\delta^k f_i = \delta^{k-1} f_{i+\frac{1}{2}} - \delta^{k-1} f_{i - \frac{1}{2}}\)，其中 \(f_{i \pm \frac{1}{2}} = f(x_i \pm \dfrac{h}{2})\)

Some Important Properties⚓︎

• 线性：\(\Delta(a \cdot f(x) + b \cdot g(x)) = a \Delta f + b \Delta g\)
• 如果 \(f(x)\) 是一个 \(m\) 阶多项式，那么 \(\Delta^k f(x)\ (0 \le k \le m)\) 是一个 \(m - k\) 阶多项式且 \(\Delta^k f(x) = 0\ (k > m)\)

• 差值还能从以下函数中得到：

  • \(\Delta^n f_k = \sum\limits_{j=0}^n (-1)^j \left( \begin{array}{cccc}n \\ j\end{array}\right) f_{n+k-j}\)
  • \(\nabla^n f_k = \sum\limits_{j=0}^n (-1)^{n-j} \left( \begin{array}{cccc}n \\ j\end{array}\right) f_{k+j-n}\)

• 反之亦然：\(f_{n+k} = \sum\limits_{j=0}^n \left( \begin{array}{cccc}n \\ j\end{array}\right) \Delta^j f_k\)

• \(f[x_0, \dots, x_k] = \dfrac{\Delta^k f_0}{k! h^k}, f[x_n, x_{n-1}, \dots, x_{n-k}] = \dfrac{\nabla^k f_n}{k!h^k}\)。从 \(R_n\) 可以得到：\(f^{(k)}(\xi) = \dfrac{\Delta^k f_0}{h^k}\)

Hermite Interpolation⚓︎

目标：找到一个密切多项式 \(P(x)\)，使得 \(\forall i = 0, 1, \dots, n, P(x_i) = f(x_i), P'(x_i) = f'(x_i), \dots, P^{(m_i)}(x_i) = f^{(m_i)}(x_i)\)。

一般情况下，给定 \(x_0, \dots, x_n; y_0, \dots, y_n\) 以及 \(y_0', \dots, y_n'\)，埃尔米特多项式 \(H_{2n+1}(x)\) 满足对于所有的 \(i\)，\(H_{2n+1}(x_i) = y_i\) 且 \(H_{2n+1}'(x_i) = y_i'\)

思考

题目答案

给定 \(x_i = i + 1, i = 0, 1, 2, 3, 4, 5\)，哪一个是 \(\widehat{h_2}(x)\)？

例子

例 1 例 2

题目解答

假设 \(x_0 \ne x_1 \ne x_2\)。给定 \(f(x_0), f(x_1), f(x_2)\) 和 \(f'(x_1)\)，寻找多项式 \(P(x)\)，满足 \(P(x_i) = f(x_i),\ i = 0, 1, 2\)，且 \(P'(x_1) = f'(x_1)\)。并分析误差。

首先，\(P(x)\) 的阶必须 \(\le 3\)（本题给出 4 个条件（3 个函数值 + 1 个导数值），根据前面“注”的第一条，最多能确定 3 阶多项式）。

与拉格朗日多项式类似，我们假设埃尔米特多项式的形式为：\(P_3(x) = \sum\limits_{i=0}^2 f(x_i) h_i(x) + f'(x_1) \widehat{h_1}(x)\)。接着根据已知条件，用待定系数法可以得到：

\[h_i(x_j) = \delta_{ij}, h_i'(x_1) = 0, \widehat{h_1}(x_i) = 0, \widehat{h_1}'(x_1) = 1\]

• \(h_0(x)\)：有根 \(x_1, x_2\)，且 \(h_0'(x_1) = 0 \quad \Rightarrow \quad x_1\) 是一个重根
  • \(\begin{cases}h_0(x) = C_0(x - x_1)^2(x - x_2) \\ h_0(x_0) = 1 \Rightarrow C_0\end{cases} \quad \Rightarrow \quad h_0(x) = \dfrac{(x - x_1)^2(x - x_2)}{(x_0 - x_1)^2(x_0 - x_2)}\)
• \(h_2(x)\)：与 \(h_0(x)\) 类似
• \(h_1(x)\)：有根 \(x_0, x_2 \Rightarrow h_1(x) = (Ax + B)(x - x_0)(x - x_2)\)。\(A, B\) 可通过 \(h_1(x_1) = 0\) 和 \(h_1'(x_1) = 0\) 求解
• \(\widehat{h_1}(x)\)：有根 \(x_0, x_1, x_2 \Rightarrow \widehat{h_1}(x) = C_1(x - x_0)(x - x_1)(x - x_2)\)。\(h_1(x_1) = 1 \Rightarrow C_1\) 能被求解

其误差分析类似拉格朗日误差分析：

\[ \begin{align} R_3(x) & = f(x) - P_3(x) \notag \\ & = K(x)(x - x_0)(x - x_1)^2(x - x_2) \notag \\ & \Rightarrow K(x) = \dfrac{f^{(4)}(\xi_x)}{4!} \notag \end{align} \]

题目解答

根据已知条件，可以得到：

\[ h_0(x) = \begin{cases}h_0(1) = 1 \\ h_0'(1) = 0 \\ h_0(2) = 0 \end{cases} \quad \widehat{h_0}(x) = \begin{cases}\widehat{h_0}(1) = 0 \\ \widehat{h_0'}(1) = 1 \\ \widehat{h_0}(2) = 0 \end{cases} \quad h_1(x) = \begin{cases}h_1(1) = 0 \\ h_1'(1) = 0 \\ h_1(2) = 1 \end{cases} \]

下面按照从易到难的顺序求解这 3 个未知量：

• 求解 \(h_1(x)\)
  • 由条件知，\(x = 1\) 是二重根
  • 那么可以令 \(h_1(x) = C(x - 1)^2\)
  • 再利用剩下那个条件，代进去计算，解得 \(C = 1\)
  • 所以 \(h_1(x) = (x - 1)^2\)
• 求解 \(\widehat{h_0}(x)\)
  • 由条件知，\(x = 1, x = 2\) 均为该函数的根
  • 那么可以令 \(\widehat{h_0}(x) = C(x - 1)(x - 2)\)
  • 利用剩下的导数条件（需要先对 \(\widehat{h_0}(x)\) 求导），解得 \(C = -1\)
  • 所以 \(\widehat{h_0}(x) = -(x - 1)(x - 2)\)
• 求解 \(h_0(x)\)
  • 由于根据已知条件只能确定 \(x = 2\) 是其中一根，另一根未知，所以只好假设 \(h_0(x) = ax^2 + bx + c\)
  • 将三个条件代进去，得到三元一次方程，解得 \(a = -1, b = 2, c = 0\)
  • 所以 \(h_0(x) = -x^2 + 2x = x(2 - x)\)

定理

如果 \(f \in C^1[a, b]\) 且 \(x_0, \dots, x_n \in [a, b]\) 是不同的数，那么在函数 \(f\) 及其导数 \(f'\) 一致的最小次数唯一多项式即为次数不超过 \(2n+1\) 的埃尔米特多项式：

\[ H_{2n+1}(x) = \sum\limits_{j=0}^n f(x_j) H_{n,j}(x) + \sum\limits_{j=0}^n f'(x_j) \widehat{H}_{n,j}(x) \]

其中 \(H_{n,j} = [1 - 2(x - x_j) L'_{n,j}(x_j)]L_{n,j}^2(x)\)，\(\widehat{H}_{n,j}(x) = (x - x_j) L^2_{n,j}(x)\)。在这里，\(L_{n,j}(x)\) 指代的是 \(n\) 阶多项式中第 \(j\) 个拉格朗日系数。

另外，若 \(f \in C^{2n-2}[a, b]\)，那么

\[ f(x) = H_{2n+1}(x) + \dfrac{(x - x_0)^2 \dots (x - x_n)^2}{(2n+2)!}f^{(2n+2)}(\xi) \]

\(\xi\) 为某个满足 \(a < \xi < b\) 的数。

证明

Step 1  for i = 1, 2, ..., n do Step 2 and 3:
    Step 2  Set z[2*i] = x[i];
                z[2*i+1] = x[i];
                Q[2*i][0] = f(x[i]);
                Q[2*i+1][0] = f(x[i]);
                Q[2*i+1][1] = f`(x[i]);
    Step 3  if i != 0 then set Q[2*i][1] = (Q[2*i][0] - Q[2*i-1][0]) / (z[2*i] - z[2*i-1]);
Step 4  for i = 2, 3, ..., 2*n+1:
            for j = 2, 3, ..., i set Q[i][j] = (Q[i][j-1] - Q[i-1][j-1]) / (z[i] - z[i-j]);
Step 5  Output(Q[0][0], Q[1][1], ..., Q[2*n+1][2*n+1]);
        STOP.

Cubic Spline Interpolation⚓︎

例子

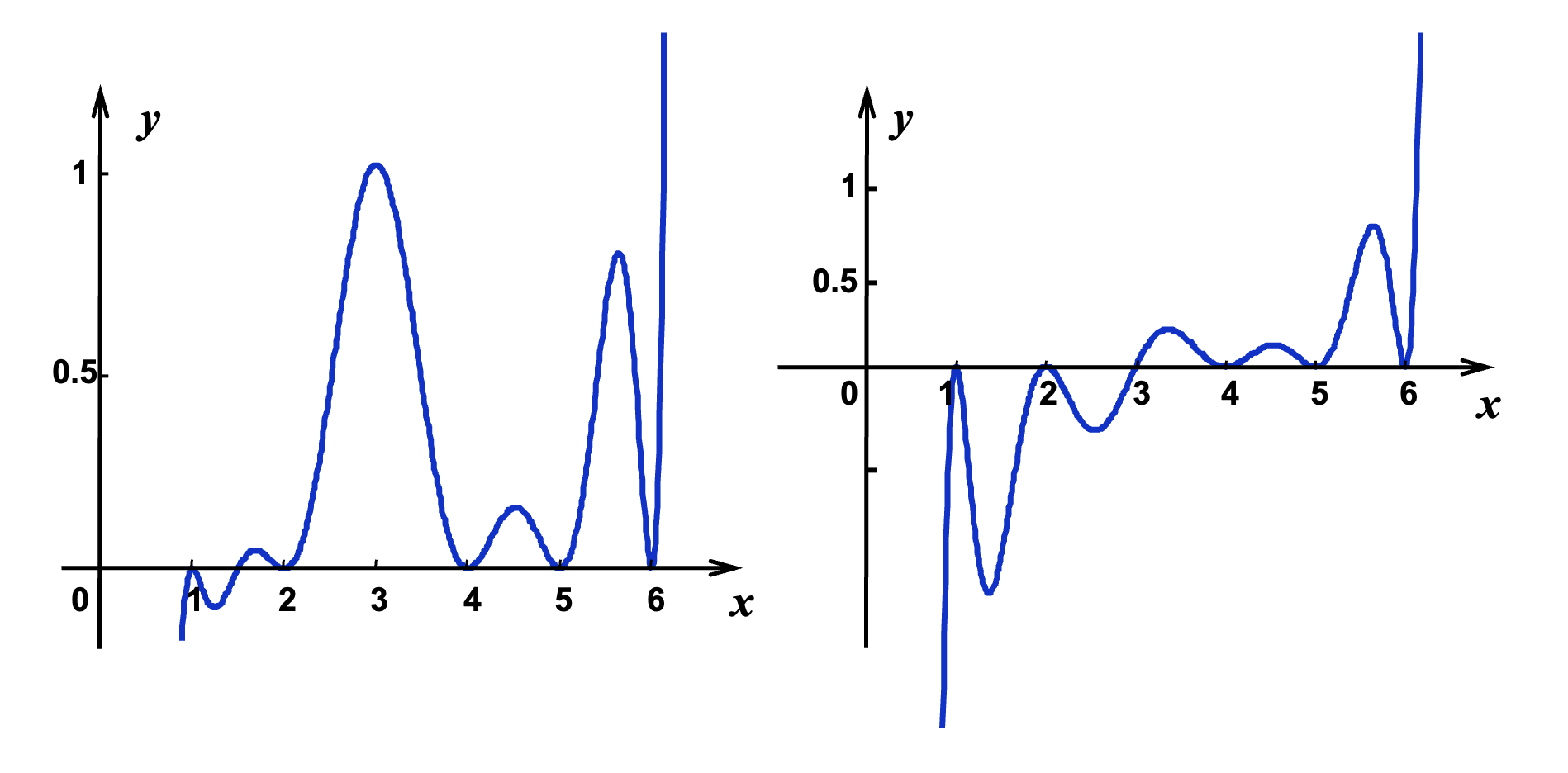
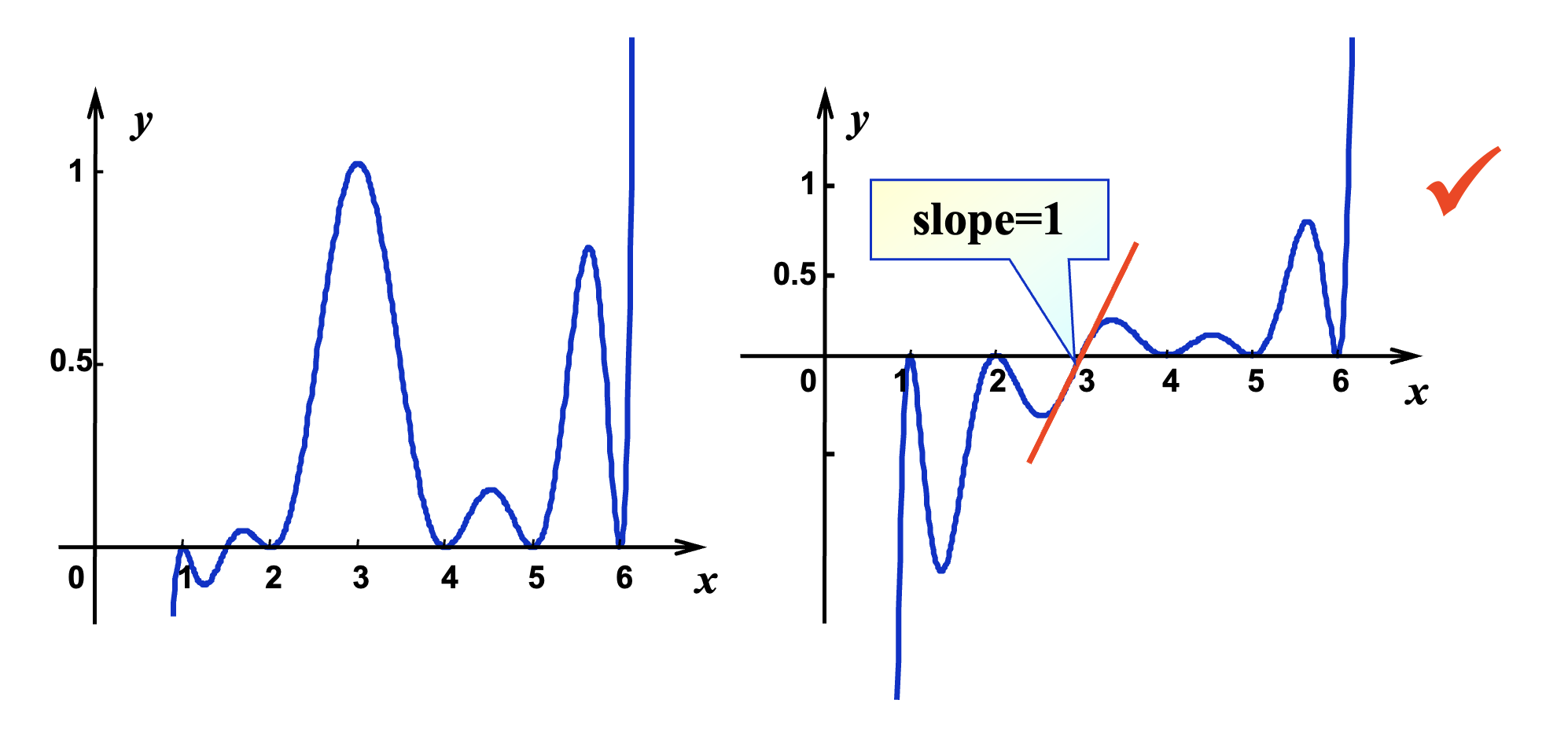
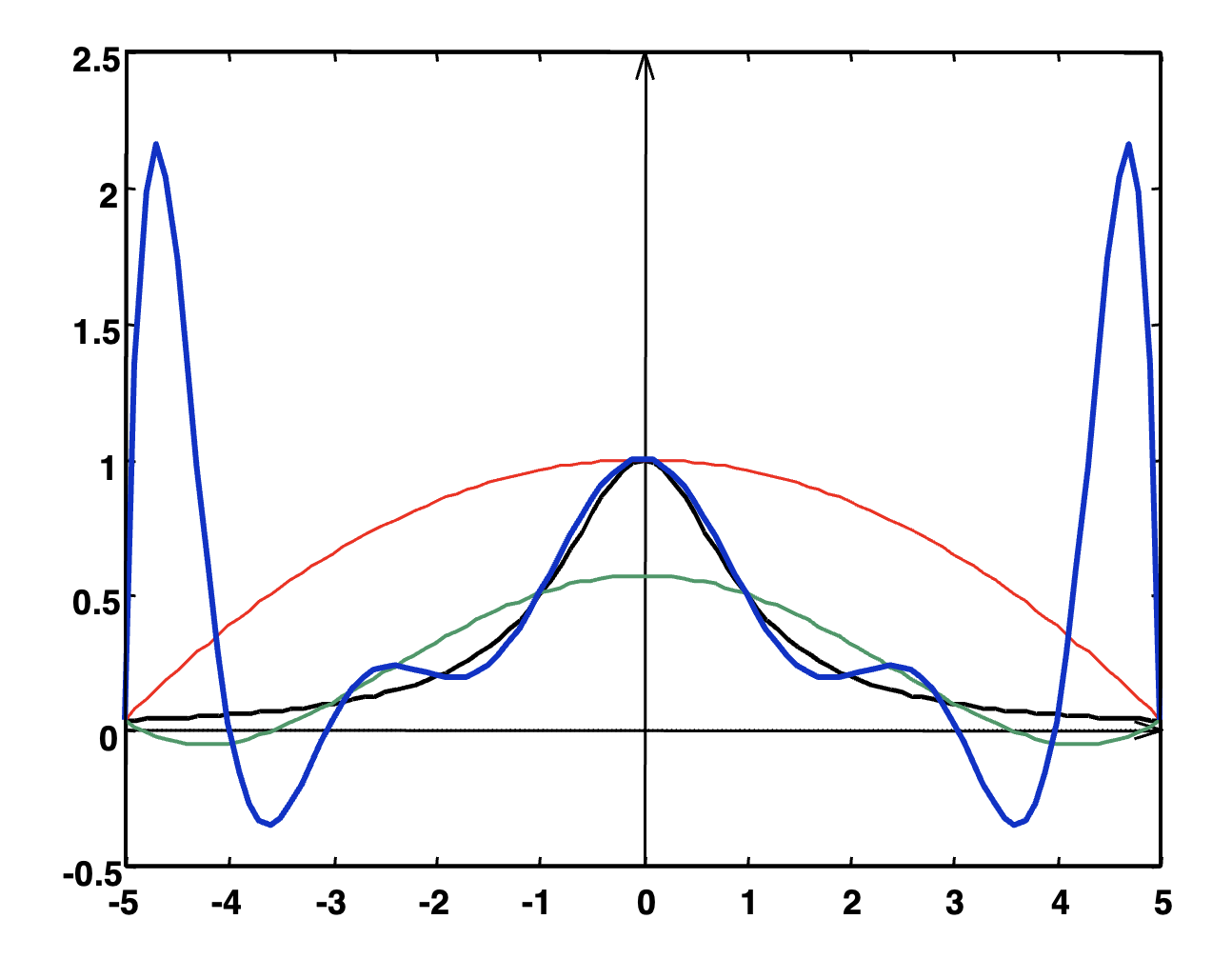
考虑关于函数 \(f(x) = \dfrac{1}{1 + x^2}\) 在点 \(x_i = -5 + \dfrac{10}{n}i \in [-5, 5] \ (i = 0, \dots, n)\) 的拉格朗日多项式 \(P_n(x)\)

可以看到，我们无法用多项式（这些彩色曲线）较为准确地近似函数（黑色曲线）。正如前面所说，增加多项式的阶数不能保证更好的近似结果，因为高阶多项式更容易发生振荡(oscillation)，反而会加大误差（即龙格现象(Runge's phenomenon)）。

这里介绍一种更好的方法：三次样条插值(cubic spline interpolation)。

wiki：样条

定义

给定一个定义在 \([a, b]\) 上的函数 \(f\)，以及一组节点 \(a = x_0 < x_1 \dots < x_n = b\)，关于 \(f\) 的三次样条插值器(cubic spline interpolant) \(S\) 是一个满足下面条件的函数：

• \(S(x)\) 是一个分段函数，在每个子区间 \([x_i, x_{i+1}]\) 上是一个三次多项式 \(S_i(x)\)（\(i = 0, 1, \dots, n - 1\)）
• \(S(x_i) = f(x_i),\ i = 0, 1, \dots, n\)
• \(S_{i+1}(x_{i+1}) = S_i(x_{i+1}),\ i = 0, 1, \dots, n - 2\)
• \(S_{i+1}'(x_{i+1}) = S_i'(x_{i+1}),\ i = 0, 1, \dots, n - 2\)
• \(S_{i+1}''(x_{i+1}) = S_i''(x_{i+1}),\ i = 0, 1, \dots, n - 2\)

后面三个条件确保了三次样条插值的光滑性。

Method of Bending Moment⚓︎

令 \(h_j = x_j - x_{j-1}\) 且 对于 \(x \in [x_{j-1}, x_j],\ S(x) = S_j(x)\)（\(S_j(x)\) 是 3 阶多项式），那么 \(S_j''(x)\) 是一个 1 阶多项式，并能通过 \(f\) 上的 2 个节点值确定下来。

假设 \(S_j''(x_{j-1}) = M_{j-1}, S_j''(x_j) = M_j\)（弯矩(bending moment)），那么 \(\forall x \in [x_{j-1}, x_j]\)，\(S_j''(x) = M_{j-1} \dfrac{x_j - x}{h_j} + M_j \dfrac{x - x_{j-1}}{h_j}\)

对 \(S_j''\) 积分，可以得到：

• \(S_j'(x) = -M_{j-1} \dfrac{(x_j - x)^2}{2h_j} + M_{j-1} \dfrac{(x - x_{j-1})^2}{2h_j} + A_j\)
• \(S_j(x) = M_{j-1} \dfrac{(x_j - x)^3}{6h_j} + M_{j-1} \dfrac{(x - x_{j-1})^3}{6h_j} + A_jx + B_j\)

其中 \(A_j, B_j\) 能通过方程 \(S_j(x_{j-1}) = y_{j-1}, S_j(x_j) = y_j\) 求解。可以得到：

• \(A_j = \dfrac{y_j - y_{j-1}}{h_j} - \dfrac{M_j - M_{j-1}}{6}h_j\)
• \(A_j x + B_j = (y_{j-1} - \dfrac{M_{j-1}}{6} h_j^2) \dfrac{x_j - x}{h_j} + (y_j - \dfrac{M_j}{6}h_j^2)\dfrac{x - x_{j-1}}{h_j}\)

现在我们来求解 \(M_j\)：因为 \(S'\) 在 \(x_j\) 上是连续的，所以：

• \([x_{j-1}, x_j]\): \(S_j'(x) = -M_{j-1} \dfrac{(x_j - x)^2}{2h_j} + M_j \dfrac{(x - x_{j-1})^2}{2h_j} + f[x_{j-1}, x_j] - \dfrac{M_j - M_{j-1}}{6}h_j\)
• \([x_j, x_{j+1}]\): \(S_{j+1}'(x) = -M_j \dfrac{(x_{j+1} - x)^2}{2h_{j+1}} + M_{j+1} \dfrac{(x - x_j)^2}{2h_{j+1}} + f[x_j, x_{j+1}] - \dfrac{M_{j+1} - M_j}{6}h_{j+1}\)

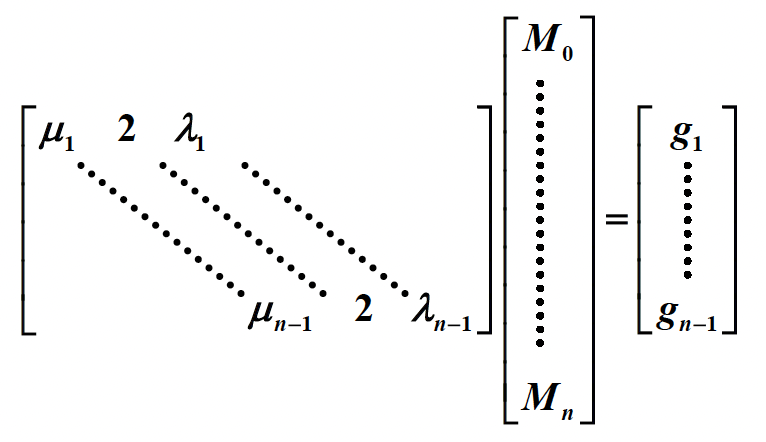
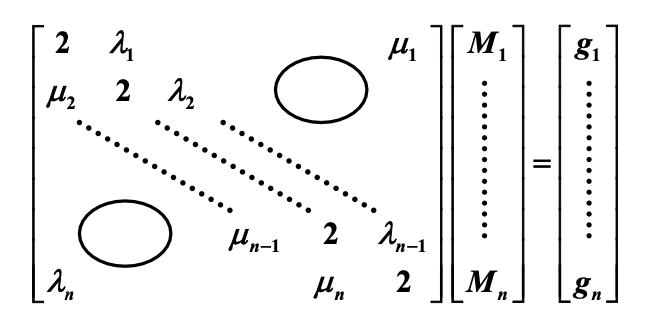
根据 \(S_j'(x_j) = S_{j+1}'(x_j)\)，我们可以结合 \(M_{j-1}, M_j, M_{j+1}\) 的系数——定义 \(\lambda_j = \dfrac{h_{j+1}}{h_j + h_{j+1}}, \mu_j = 1 - \lambda_j, g_j = \dfrac{6}{h_j + h_{j+1}} (f[x_j, x_{j+1}] - f[x_{j-1}, x_j])\)，可以得到：\(\mu_j M_{j-1} + 2M_j + \lambda_j M_{j+1} = g_j\ (1 \le j \le n - 1)\)（下图就是这个递推式的矩阵表示（一个三对角矩阵））。也就是说，我们有 \(n+1\) 个未知数，但只有 \(n-1\) 个方程，所以还需要 2 个额外的边界条件。

• 固定边界(clamped boundary)：\(S'(a) = y_0', S'(b) = y_n'\)

  • \([a, x_1]\): \(S_1'(x) = -M_0 \dfrac{(x_1 - x)^2}{2h_1} + M_1 \dfrac{(x - a)^2}{2h_1} + f[x_0, x_1] - \dfrac{M_1 - M_0}{6}h_1\)
  • 在 \([x_{n-1}, b]\) 上 \(S_n'\) 也是类似的：\(\begin{cases}2M_0 + M_1 = \dfrac{6}{h_1} (f[x_0, x_1] - y_0') = g_0 \\ M_{n-1} + 2M_n = \dfrac{6}{h_n} (y_n' - f[x_{n-1}, x_n]) = g_n\end{cases}\)
  算法：固定三次样条

  

  

• 自由边界(free boundary)：\(S''(a) = y_0'' = M_0, S''(b) = y_n'' = M_n\)，且 \(M_0 = M_n = 0\) 时

  • 那么 \(\lambda_0 = 0, g_0 = 2y_0'';\ \mu_n = 0, g_n = 2y_n''\)
  • 此时的样条称为自然样条(natural spline)
  算法：自然三次样条

  

  

• 周期边界(periodic boundary)：如果 \(f\) 是周期函数，即 \(y_n = y_0\) 且 \(S'(a^+) = S'(b^-) \Rightarrow M_0 = M_n\)

  

对应的作业练习📝

对应小测 7💯