Chap 6: Direct Methods for Solving Linear Systems⚓︎
约 4445 个字 90 行代码 预计阅读时间 23 分钟
核心知识
- 高斯消元法
- 一些选取主元的策略
- 部分主元法
- 缩放部分主元法
- 完全主元法
- 矩阵分解:LU 分解
- 一些特殊矩阵
- 严格对角占优矩阵
- 正定矩阵 -> Choleski 法
- 三对角矩阵 -> Crout 分解
目标:求解 \(A \bm{x} = \bm{b}\)
注
在继续第 6 章(以及第 7 章)的学习前,建议先回顾线性代数的知识,否则理解起来可能比较吃力(但有些内容就是线性代数中学过的,比如下面的高斯消元法
逆矩阵的求解
个人比较喜欢高斯 - 约旦消元法(Gauss-Jordan elimination)(计算机也常用这种方法
- 构造增广矩阵 \([A | I]\)
- 对增广矩阵进行行初等变换(目标是将左侧的 \(A\) 变为单位矩阵 \(I\)
) :- 交换两行。
- 将某一行乘以一个非零常数。
- 将某一行的一个倍数加到另一行。
- 检查结果:如果左侧成功变为 \(I\),则右侧的矩阵就是 \(A^{-1}\)。如果左侧在变换过程中出现全零行(或列
) ,则 \(A\) 不可逆。
Linear Systems for Equations⚓︎
Gaussian Elimination⚓︎
高斯消元法(Gaussian elimination) 的基本思路:
- 首先将矩阵 \(A\) 归约成一个上三角(upper-triangular) 矩阵
- 然后通过回代(backward-substitution) 来求解未知量
先来看消元(elimination) 的实现:先令 \(A^{(1)} = A = (a_{ij}^{(1)})_{n \times n}, \bm{b}^{(1)} = \bm{b} = \begin{bmatrix}b_1^{(1)} \\ \vdots \\ b_n^{(1)}\end{bmatrix}\)
-
第 1 步:
- 如果 \(a_{11}^{(1)} \ne 0\),计算 \(m_{i1} = \dfrac{a_{i1}^{(1)}}{a_{11}^{(1)}}, (i = 2, \dots, n)\)
-
那么增广矩阵 (augmented matrix) 的第 \(i\) 行 \(\text{row}_i\) 为:\(m_{i1} \times \text{row}_1\),得到
\[ \left[ \begin{array}{cccc|c} a_{11}^{(1)} & a_{12}^{(1)} & \cdots & a_{1n}^{(1)} & b_1^{(1)} \\ 0 & & A^{(2)} & & \bm{b}^{(2)} \\ \end{array} \right] \]其中 \(\begin{cases}a_{ij}^{(2)} = a_{ij}^{(1)} - m_{i1} a_{1j}^{1} \\ b_i^{(2)} = b_i^{(1)} - m_{i1} b_1^{(1)}\end{cases}, (i, j = 2, \dots, n)\)
-
第 k 步:
- 如果 \(a_{kk}^{(k)} \ne 0\),计算 \(m_{ik} = \dfrac{a_{ik}^{(k)}}{a_{kk}^{(k)}}, (i = k+1, \dots, n)\)
- \(\begin{cases}a_{ij}^{(k+1)} = a_{ij}^{(k)} - m_{ik} a_{kj}^{k} \\ b_i^{(k+1)} = b_i^{(k)} - m_{ik} b_k^{(k)}\end{cases}, (i, j = k+1, \dots, n)\)
-
n-1 步后:
\[ \begin{bmatrix} a_{11}^{(1)} & a_{12}^{(1)} & \dots & a_{1n}^{(1)} \\ & a_{22}^{(2)} & \dots & a_{2n}^{(2)} \\ & & \dots & \vdots \\ & & & a_{nn}^{(n)}\end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n\end{bmatrix} = \begin{bmatrix}b_1^{(1)} \\ b_2^{(2)} \\ \vdots \\ b_n^{(n)}\end{bmatrix} \]
接下来看回代:
- \(x_n = \dfrac{b_n^{(n)}}{a_{nn}^{(n)}}\)
- \(x_i = \dfrac{b_i^{(i)} - \sum\limits_{j=i+1}^n a_{ij}^{(i)} x_j}{a_{ii}^{(i)}}, (i = n - 1, \dots, 1)\)
- 我们必须找到最小的整数 \(k \ge i\) 且 \(a_{ki}^{(i)} \ne 0\),然后交换第 \(k\) 行和第 \(i\) 行
代码实现
求解 \(n \times n\) 线性方程组:
- 输入:未知量和方程的数量 \(n\);增广矩阵 \(A = (a_{ij})\),其中 \(1 \le i \le n, 1 \le j \le n+1\)
- 输出:解 \(x_1, x_2, \dots, x_n\),或者线性方程组没有唯一解的信息
Step 1 for i = 1, ..., n - 1 do Steps 2-4:
Step 2 Let p be the smallest integer with i <= p <= n and a[p][i] != 0;
if no integer p can be found
then Output('no unique solution exists');
STOP;
// row exchange
Step 3 if p != i then perform (E[p]) <-> (E[i]);
// elimination
Step 4 for j = i + 1, ..., n do Step 5 and 6:
Step 5 Set m[j][i] = a[j][i] / a[i][i]
Step 6 Perform (E[j] - m[j][i] * E[i]) -> (E[i])
Step 7 if a[n][n] = 0 then Output('no unique solution exists');
STOP;
// backward substitution
Step 8 Set x_n = a[n][n+1] / a[n][n]
Step 9 for i = n - 1, ..., 1 set x[i] = [a[i][n+1] - sum(j=i+1, n, a[i][j] * x[j])] / a[i][i];
Step 10 Output(x[1], ..., x[n]);
STOP; // success
Amount of Computation⚓︎
现在我们来统计一下计算量(仅考虑乘法 / 除法
- 消元:\(\sum\limits_{k=1}^{n-1} (n - k)(n - k + 2) = \dfrac{n^3}{3} + \dfrac{n^2}{2} - \dfrac{5}{6}n\)
- 回代:\(1 + \sum\limits_{i=1}^{n-1}(n - i + 1) = \dfrac{n^2}{2} + \dfrac{n}{2}\)
所以对于很大的 \(n\),乘法和除法的总数大约为 \(\textcolor{red}{\dfrac{n^3}{3}}\)。也就是说,高斯消元法的时间复杂度为 \(O(n^3)\)。
Pivoting Strategies⚓︎
除非有特殊说明,以下的 \(k\) 指的是第 \(k\) 次高斯消元。
一般高斯消元法的问题
在高斯消元的过程中,如果其中一个主元(pivot) \(a_{kk}^{(k)} = 0\),那么就需要进行行交换 \((E_k) \leftrightarrow (E_p)\),其中 \(p\) 是最小的满足 \(p > k\) 且 \(a_{pk}^{(k)} \ne 0\) 的整数。但为了减小舍入误差,即使主元并不等于 0 的时候也要做行交换。
如果 \(a_{kk}^{(k)}\) 相比 \(a_{jk}^{(k)}\) 较小的话,那么乘数 \(m_{jk} = \dfrac{a_{jk}^{(k)}}{a_{kk}^{(k)}}\) 会大于 1,导致误差的积累。并且在回代的时候,\(x_k\) 的值因为分母 \(a_{kk}^{(k)}\) 的值过小,其计算误差也会被放大。
所以,我们需要选取合适的主元以减小误差。下面给出一些选取主元的策略。
置换矩阵
找到合适的主元后,一般我们会做一个行交换。在后面涉及到矩阵分解的时候
比如 \(P_{12} = \begin{bmatrix}0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1\end{bmatrix}\) 表示交换第 1 行和第 2 行。如果 \(\bm{x} = \begin{bmatrix}x_1 \\ x_2 \\ x_3\end{bmatrix}\),那么 \(P_{12} \bm{x} = \begin{bmatrix}x_2 \\ x_1 \\ x_3\end{bmatrix}\)。
Partial Pivoting⚓︎
部分主元法(partial pivoting)(或称为最大列主元法 (maximal column pivoting)
代码实现
求解 \(n \times n\) 线性方程组:
- 输入:未知量和方程的数量 \(n\);增广矩阵 \(A = (a_{ij})\),其中 \(1 \le i \le n, 1 \le j \le n+1\)
- 输出:解 \(x_1, x_2, \dots, x_n\),或者线性方程组没有唯一解的信息
Step 1 for i = 1, ..., n set NROW(i) = i; // initialize row pointer
Step 2 for i = 1, ..., n - 1 do Steps 3-6: // elimination process
Step 3 Let p be the smallest integer with i <= p <= n and
|a(NROW(p), i)| = max_{i <= j <= n}|a(NROW(j), i)|;
Step 4 if a(NROW(p), i) = 0 then Output('no unique solution exists');
STOP;
Step 5 if NROW(i) != NROW(p) then set NCOPY = NROW(i); // simulated row interchange
NROW(i) = NROW(p);
NROW(p) = NCOPY;
Step 6 for j = i + 1, ..., n do Steps 7-8:
Step 7 Set m(NROW(j), i) = a(NROW(j), i) / a(NROW(i), i);
Step 8 Perform (E_NROW(j) - m(NROW(j), i) * E_NROW(i)) -> (E_NROW(j));
Step 9 if a(NROW(n), n) = 0 then Output('no unique solution exists');
STOP;
// start backward substitution
Step 10 Set x[n] = a(NROW(n), n + 1) / a(NROW(n), n);
Step 11 for i = n - 1, ..., 1
set x[i] = (a(NROW(i), n + 1) - sum(j=i+1, n, a(NROW(i), j) * x[j])) / a(NROW(i), i);
Step 12 Output(x[1], ..., x[n]); // procedure completed successfully
STOP;
例子
求解线性方程组 \(\begin{cases}30.00 x_1 + 594100 x_2 = 591700 \\ 5.291 x_1 - 6.130 x_2 = 46.78\end{cases}\),舍入精度为 4 位。
可以看到,虽然根据部分主元法,解方程时无需交换行,然而注意到第一个方程中同一行的元素量级相差巨大,而第二行元素的量级比较接近,所以会产生较大的误差(这也反映了部分主元法的缺陷
Scaled Partial Pivoting⚓︎
缩放部分主元法(scaled partial pivoting)(或称为缩放列主元法 (scaled-column pivoting)
- 第 1 步:定义每一行的缩放因子(scale factor) \(s_i = \max\limits_{1 \le j \le n} |a_{ij}|\)(即每行中绝对值最大的元素)
- 第 2 步
: (对于第 \(k\) 次高斯消元, )找到最小的 \(p \ge k\),使得 \(\dfrac{|a_{pk}^{(k)}|}{s_p} = \max\limits_{k \le i \le n} \dfrac{|a_{ik}^{(k)}|}{s_i}\),然后交换第 \(p\) 行和第 \(k\) 行
注
缩放因子只计算一次(在高斯消元前
代码实现
和部分主元法的实现相比,区别在于前 3 步,后续步骤都是一样的,因此下面只列出前 3 步:
Step 1 for i = 1, ..., n set s_i = max_{1 <= j <= n}(|a_ij|);
if s_i = 0 then Output('no unique solution exists');
STOP;
Step 2 for i = 1, ..., n - 1 do Steps 3-6: // elimination process
Step 3 Let p be the smallest integer with i <= p <= n and
|a(NROW(p), i)| / s(NROW(p)) = max_{i <= j <= n}(|a(NROW(j), i)| / s(NROW(j)));
缩放部分主元法的好处在哪里?
一般的部分主元法考虑的是绝对大小(当前列绝对值最大的元素
Complete Pivoting⚓︎
完全主元法(complete pivoting)(或称为最大主元法 (maximal pivoting)
Amount of Computation⚓︎
- 部分主元法:需要 \(O(n^2)\) 次比较
- 缩放部分主元法:需要 \(O(n^2)\) 次比较,以及 \(O(n^2)\) 次除法(初始计算)
- 完全主元法:需要 \(O(\dfrac{n^3}{3})\) 次比较
所以,要想追求更好的稳定性,就要以更大的计算量为代价。
注
如果新的缩放因子在行交换的时候才被确定,那么缩放部分主元法需要 \(O(\dfrac{n^3}{3})\) 次额外的比较,以及 \(O(n^2)\) 次除法
Matrix Factorization⚓︎
高斯消元法是一种简单粗暴的方法,但效率不是很高。因此下面介绍一种基于高斯消元法实现的改进方法——矩阵分解(matrix factorization)。它的计算过程如下:
-
第 1 步:
- \(m_{i1} = \dfrac{a_{i1}}{a_{11}} (a_{11} \ne 0)\)
- 令 \(L_1 = \begin{bmatrix}1 & & & \\ -m_{21} & 1 & & \\ \vdots & & \ddots \\ -m_{n1} & & &1\end{bmatrix}\)(这就是第一高斯变换矩阵(first Gaussian transformation matrix)
) ,那么 \(L_1 [A^{(1)} \quad \bm{b}^{(1)}] = \begin{bmatrix}a_{11}^{(1)} & \dots a_{1n}^{(1)} & b_1^{(1)} \\ 0 & A^{(2)} & \bm{b}^{(2)}\end{bmatrix}\)
-
第 k 步:
- 第 k 高斯变换矩阵(kth Gaussian transformation matrix):\(L_k = \begin{bmatrix}1 & & & & \\ & \ddots & & & \\ & & 1 & & \\ & & -m_{k+1, k} & & \\ & & \vdots &\ddots & \\ & & -m_{n, k} & & 1\end{bmatrix}\)(空的地方都是 0)
-
第 n-1 步:
\[ L_{n-1}L_{n-2} \dots L_1 [A \quad \bm{b}] = \begin{bmatrix}a_{11}^{(1)} & a_{12}^{(1)} & \dots & a_{1n}^{(1)} & b_1^{(1)}\\ & a_{22}^{(2)} & \dots & a_{2n}^{(2)} & b_2^{(2)} \\ & & \dots & \vdots & \vdots\\ & & & a_{nn}^{(n)} & b_n^{(n)}\end{bmatrix} \]
定理
若高斯消元法能够在不使用行互换的基础上求解线性方程组 \(A \bm{x} = \bm{b}\),那么矩阵 \(A\) 可以被因式分解为一个下三角矩阵 \(L\) 和上三角矩阵 \(U\) 的乘积,即 \(A = LU\)。
其中:
如果矩阵 \(L\) 是单位的(unitary)(也就是说主对角线元素都是 1
唯一性证明
如果分解不是唯一的,那么存在 \(L_1, L_2, U_1, U_2\),使得 \(A = L_1 U_1 = L_2 U_2\),因此:
注
如果 \(U\) 也是单位的,那么这种分解就称为Crout 分解。我们可通过对 \(A^T\) 的 \(LU\) 分解来实现 Crout 分解。也就是说,找到 \(A^T = LU\),那么 \(A = U^T L^T\) 就是 \(A\) 的 Crout 分解。
\(LU\) 分解的代码实现
将 \(n \times n\) 的矩阵 \(A = (a_{ij})\) 分解为下三角矩阵 \(L = (l_{ij})\) 和上三角矩阵 \(U = (u_{ij})\),也就是说 \(A = LU\),其中 \(L\) 或 \(U\) 的主对角线元素均为 1。
- 输入:维度 \(n\);\(A\) 的元素 \(a_{ij}, 1 \le i, j \le n\);\(L\) 的对角元素 \(l_{11} = \dots = l_{nn} = 1\) 或 \(U\) 的对角元素 \(u_{11} = \dots = u_{nn} = 1\)
- 输出:\(L\) 的项 \(l_{ij}, 1 \le j \le i, 1 \le i \le n\),以及 \(U\) 的项 \(u_{ij}, i \le j \le n, 1 \le i \le n\)
Step 1 Select l_11 and u_11 satisfying l_11 * u_11 = a_11;
if l_11 * u_11 = 0 then Output('Factorization impossible');
Stop;
Step 2 for j = 2, ..., n set u_1j = a_1j / l_11; // first row of U
l_j1 = a_j1 / u_11; // first column of L
Step 3 for i = 2, ..., n - 1 do Steps 4 and 5:
Step 4 Select l_ii and u_ii safisfying l_ii * u_ii = a_ii - sum(k=1, i-1, l_ik * u_ki);
if l_ii * u_ii = 0 then Output('Factorization impossible');
Stop;
Step 5 for j = i + 1, ..., n:
set u_ij = 1 / l_ii * (a_ij - sum(k=1, i-1, l_ik * u_kj)); // ith row of U
set l_ji = 1 / u_ii * (a_ji - sum(k=1, i-1, l_jk * u_ki)); // ith column of L
Step 6 Select l_nn and u_nn satisfying l_nn * u_nn = a_nn - sum(k=1, n-1, l_nk * u_kn);
// if l_nn * u_nn = 0, then A = LU but A is singular
Step 7 Output(l_ij for j = 1, ..., i and i = 1, ..., n);
Output(u_ij for j = i, ..., n and i = 1, ..., n);
STOP;
这样我们只得到了 \(L\) 和 \(U\),还没有解出这个线性方程组(矩阵
因为 \(A \bm{x} = LU \bm{x} = \bm{b}\),所以我们令 \(\bm{y} = U\bm{x}\),
- 先解 \(L \bm{y} = \bm{b}\)
- \(y_1 = \dfrac{b_1}{l_{11}}\)
- \(y_i = \dfrac{1}{l_{ii}} \Big[b_i - \sum\limits_{j=1}^{i-1} u_{ij} y_j\Big]\)
- 再解 \(U \bm{x} = \bm{y}\)
- \(x_n = \dfrac{y_n}{u_{nn}}\)
- \(x_i = \dfrac{1}{u_{ii}} \Big[y_i - \sum\limits_{j=i+1}^n u_{ij} x_j\Big]\)
高斯消元法 v.s. LU 分解(by Gemini 2.5 Flash)
| 特性 | 一般高斯消元法(直接对 \([A\|b]\)) | LU 分解 |
|---|---|---|
| 基本思想 | 将 \([A\|b]\) 转化为 \([U'\|b']\) | 将 \(A\) 分解为 \(L\) 和 \(U\) |
| 求解 \(Ax=b\) | 每次 \(O(N^3)\) | 分解 \(O(N^3)\),每次求解 \(O(N^2)\) |
| 多右端向量 | 每次 \(O(N^3)\) | 高效:分解一次 \(O(N^3)\),后续每次 \(O(N^2)\) |
| 计算 \(A^{-1}\) | \(O(N^4)\) | 高效:\(O(N^3)\) |
| 计算 \(\det(A)\) | 需记录消元过程 | 直接:对角线元素乘积 |
| 结构 | 紧密耦合 \(A\) 和 \(b\) | 模块化:分解与求解分离 |
| 存储 | 每次重新计算 | \(L, U\) 可存储重用 |
| 数值稳定性 | 依赖于主元选择 | 依赖于主元选择,通常与主元法结合 |
Special Types of Matrices⚓︎
Strictly Diagonally Dominant Matrix⚓︎
严格对角占优矩阵(strictly diagonally dominant matrix) 满足:
即对角线元素的绝对值是其所在行内所有元素的绝对值中的最大者。
定理
- 严格对角占优矩阵 \(A\) 是非奇异的(nonsigular)(即行列式不为 0,且存在逆矩阵)
- 在这种矩阵上使用高斯消元法无需行或列的互换
- 并且计算将相对于舍入误差的增长保持稳定
证明
- \(A\) 是非奇异的——反证法证明
- 高斯消元法无需行或列的互换——归纳法证明:通过高斯消元法得到的每一个矩阵 \(A^{(2)}, A^{(3)}, \dots, A^{(n)}\) 都是严格对角占优的
- 略过
Choleski's Method for Positive Definite Matrix⚓︎
定义
对于一个矩阵 \(A\),如果它是对称的,且 \(\forall \bm{x} \ne \bm{0}, \bm{x}^T A \bm{x} > 0\) 成立,那么称该矩阵是正定(positive definite) 矩阵。
定理
正定矩阵 \(A\) 的性质:
a. \(A\) 是非奇异的
b. \(a_{ii} > 0, i = 1, 2, \dots n\)
c. \(\max_{1 \le k, j \le n} |a_{kj}| \le \max_{1 \le i \le n} |a_{ii}|\)
d. \((a_{ij})^2 < a_{ii} a_{jj}, i \ne j\)
PPT 上还有这些性质:
- \(A^{-1}\) 也是正定的
- \(A\) 的每个前导主子矩阵(leading principal submatrices) \(A_k\) 的行列式 (determinant) 都是正的
前导主子矩阵
矩阵 \(A\) 的前导主子矩阵为 \(A_k = \begin{bmatrix}a_{11} & a_{12} & \dots & a_{1k} \\ a_{21} & a_{22} & \dots & a_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{k1} & a_{k2} & \dots & a_{kk} \end{bmatrix}, 1 \le k \le n\)
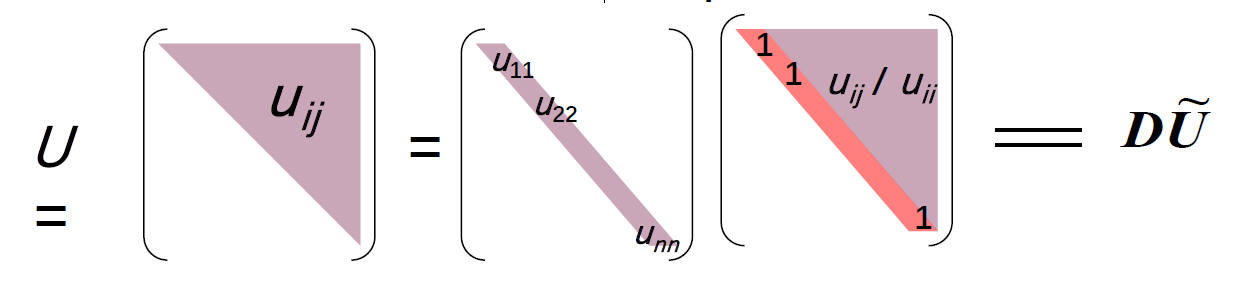
我们将 \(A = LU\) 中的 \(U\) 进一步拆分成对角矩阵 \(D\) 和单位上三角矩阵 \(\widetilde{U}\):
可以推导出:\(A\) 是对称矩阵(\(A = A^T \rightarrow LU = LD \widetilde{U} = \widetilde{U^T} DL^T\))\(\Rightarrow L = \widetilde{U}^T \Rightarrow A = LDL^T\)。这样我们得到了另一种矩阵分解—— \(LDL^T\) 分解:
\(LDL^T\) 分解的代码实现
将 \(n \times n\) 的矩阵 \(A = (a_{ij})\) 分解为 \(LDL^T\) 的形式,其中 \(L\) 是下三角矩阵,对角线元素均为 1;\(D\) 为对角矩阵,对角线上的元素均为正数。
- 输入:维度 \(n\);\(A\) 的元素 \(a_{ij}, 1 \le i, j \le n\)
- 输出:\(L\) 的项 \(l_{ij}, 1 \le j \le i, 1 \le i \le n\),以及 \(D\) 的项 \(u_{i}, 1 \le i \le n\)
令 \(D^{\frac{1}{2}} = \begin{bmatrix}\sqrt{u_{11}} & & & \\ & \sqrt{u_{22}} & & \\ & & & & \\ & & & \sqrt{u_{nn}}\end{bmatrix}\),\(\widetilde{L} = LD^{\frac{1}{2}}\) 仍然是一个上三角矩阵,因此 \(A = \widetilde{L} \widetilde{L}^T\)
因为前导主子矩阵都是正的,所以 \(u_{ii} > 0\)
综上,若 \(A\) 是正定矩阵,那么:
- 当 \(L\) 是一个对角线元素均为 1 的下三角矩阵,并且 \(D\) 是一个对角项均为正数的对角矩阵时,\(A\) 可被分解为 \(LDL^T\)
- 当 \(L\) 是一个对角线上均为非零元素的下三角矩阵时,\(A\) 可被分解为 \(LL^T\)
算法:Choleski 法
目标:将规模为 \(n \times n\) 的对称的正定矩阵 \(A\) 分解为 \(LL^T\),其中 \(L\) 是下三角矩阵。
输入:\(n\) 维矩阵 \(A\),其元素为 \(a_{ij}, 1 \le i, j \le n\)
输出:矩阵 \(L\),其元素为 \(l_{ij}, 1 \le j \le i, 1 \le i \le n\)
Step 1 set l_11 = sqrt(a_11);
Step 2 for j = 2, ..., n, set l_j1 = a_j1 / l_11;
Step 3 for i = 2, ..., n - 1 do steps 4 and 5
Step 4 set l_ii = sqrt(a_ii - sum(pow(l_ik, 2), 1, i - 1))
// LDL^T is faster, but must be modified to solve Ax = b
Step 5 for j = i + 1, ..., n, set l_ji = (a_ji - sum(l_jk * l_ik, 1, i - 1)) / l_ii;
Step 6 set l_nn = sqrt(a_nn - sum(pow(l_nk, 2), 1, n - 1))
Step 7 output (l_ij for j = 1, ..., i and i = 1, ..., n);
Stop.
Choleski 法的优点(by Gemini 2.5 Flash)
- 数值稳定性高:Choleski 法在数值上非常稳定,因为它不需要主元选择。由于矩阵是正定的,可以保证对角线元素 \(l_{ii}\) 的平方根总是正实数,并且不会出现除以零的情况。
- 计算效率高:相比于一般的 LU 分解(需要 \(2N^3/3\) 次浮点运算
) ,Choleski 法只需要大约 \(N^3/3\) 次浮点运算,因为它利用了矩阵的对称性,只需要计算 \(L\) 的下三角部分(或 \(U\) 的上三角部分) 。这使得它在处理大型对称正定系统时非常高效。 - 存储效率高:由于 \(L\) 和 \(L^T\) 之间存在关系,我们只需要存储 \(L\)(或 \(U\)
) ,这节省了存储空间。 - 保证正定性:如果 Choleski 法成功完成(即所有 \(l_{ii}\) 都是正实数
) ,则可以确认原始矩阵是正定的。反之,如果分解过程中遇到负数或零的平方根,则矩阵不是正定的。
Crout Reduction for Tridiagonal Linear System⚓︎
带状矩阵
对于一个 \(n \times n\) 的矩阵,如果有整数 \(p, q\),满足 \(1 < p, q < n\),当 \(i + p \le j\) 或 \(j + q \le i\) 时,有 \(a_{ij} = 0\),那么称该矩阵为带状矩阵(band matrix),其带宽(bandwidth) 为 \(w = p + q - 1\)。
当 \(p = q = 2\) 时,\(w = 3\),此时的矩阵称为三对角矩阵(tridiagonal matrix),其形式如下:
对于上述形式的线性方程组(\(A \bm{x} = \bm{f}\)
-
寻找矩阵 \(A\) 的 Crout 分解,\(L, U\) 分别为:
\[ L = \begin{bmatrix}l_{11} & 0 & \dots & \dots & 0 \\ l_{21} & l_{22} & \ddots & & \vdots \\ 0 & \ddots & \ddots & \ddots & 0 \\ 0 & \dots & 0 & l_{n, n-1} & l_{nn}\end{bmatrix} \quad U = \begin{bmatrix}1 & u_{12} & 0 & \dots & 0 \\ 0 & 1 & \ddots & \ddots & \vdots \\ \vdots & & \ddots & \ddots & u_{n-1, n} \\ 0 & \dots & \dots & 0 & 1\end{bmatrix} \] -
求解 \(L\bm{y} = \bm{f} \Rightarrow y_1 = \dfrac{f_1}{l_{11}}, y_i = \dfrac{(f_i - l_{i, i-1} y_{i-1})}{l_{ii}} (i = 2, \dots, n)\)
- 求解 \(U\bm{x} = \bm{y} \Rightarrow x_n = y_n, x_i = y_i - u_{i,i+1} x_{i+1}\)
定理
如果 \(A\) 是三对角线矩阵,且是对角线占优的,并满足 \(|b_1| > |c_1| > 0, |b_n| > |a_n| > 0, a_i \ne 0, c_i \ne 0\),那么 \(A\) 是非奇异的,对应的线性方程组有解。
注
- 如果 \(A\) 是严格对角占优的,那么没有必要让所有的 \(a_i, b_i, c_i\) 都是非零的
- 该方法是稳定的,因为所有从计算过程中获得的值会被约束在原有元素的范围内
- 计算量为 \(O(n)\)
代码实现
求解 \(n \times n\) 的线性方程组:
假设这个线性方程组有唯一解。
- 输入:维度 \(n\);\(A\) 的元素
- 输出:解 \(x_1, \dots, x_n\)
Step 1 Set l_11 = a_11;
u_12 = a_12 / l_11;
z_1 = a_{1,n+1} / l_11;
Step 2 for i = 2, ..., n-1 set l_{i, i-1} = a_{i, i-1}; // ith row of L
l_ii = a_ii - l_{i, i-1} * u_{i-1, i};
u_{i, i+1} = a_{i, i+1} / l_ii; // (i+1)th column of U
z_i = (a_{i, n+1} - l_{i, i-1} * z_{i-1}) / l_ii;
Step 3 Set l_{n, n-1} = a_{n, n-1}; // nth row of L
l_nn = a_nn - l_{n, n-1} * u_{n-1, n};
z_n = (a_{n, n+1} - l_{n, n-1} * z_{n-1}) / l_nn;
// Step 4 and 5 solve Ux = z
Step 4 x_n = z_n;
Step 5 for i = n-1, ..., 1 set x_i = z_i - u_{i, i+1} * x_{i+1};
Step 6 Output(x_1, ..., x_n);
STOP;
对应的作业练习📝
对应小测 3 和 4💯
评论区