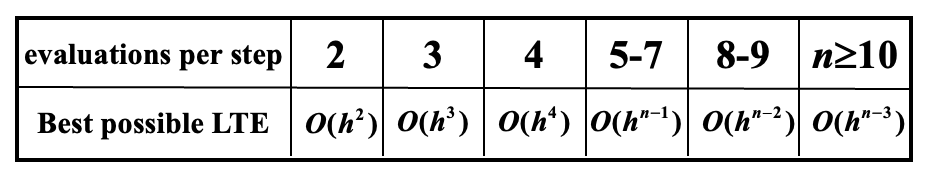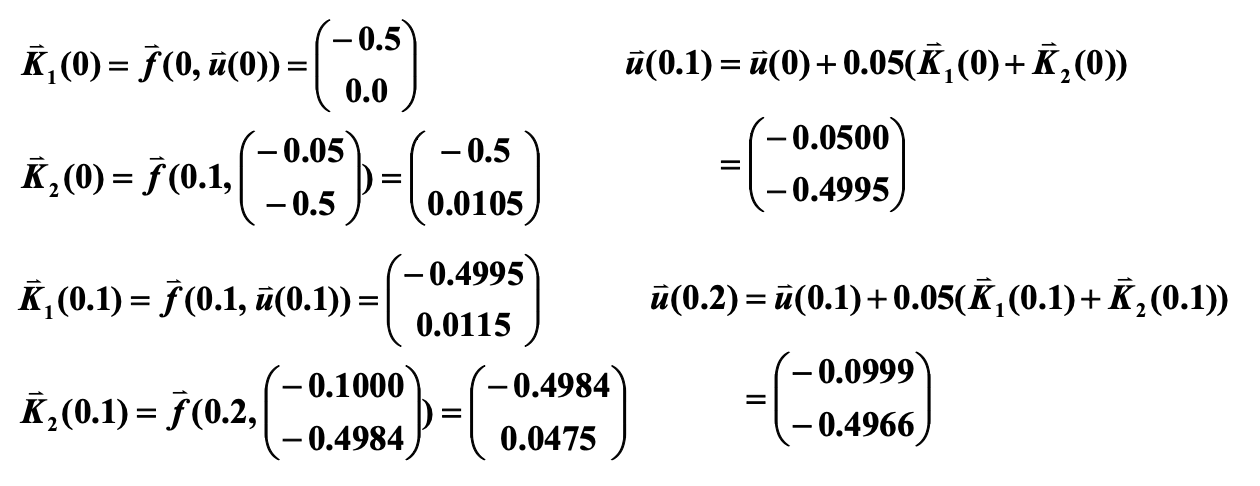Chap 5: Initial-Value Problems for Ordinary Differential Equations⚓︎

约 4435 个字预计阅读时间 22 分钟

The Elementary Theory of Initial-Value Problems⚓︎

1 阶常微分方程 (ordinary differential equations) 的初值问题(initial-value problems, IVP)：

\[ \begin{cases} \dfrac{dy}{dx} = f(t, y), t \in [a, b] \\ y(a) = \alpha \end{cases} \]

目标：在一组网格点 (mesh points) \(a = t_0 < t_1 < \dots < t_n = b\) 上（通常是等间距的）计算 \(y(t)\) 的近似值。也就是说，计算 \(w_i \approx y(t_i) = y_i\ (i = 1, \dots, n)\)。

定义

对于函数 \(f(t, y)\)，若存在常数 \(L > 0\)，满足：

\[ |f(t, y_1) - f(t, y_2)| \le L|y_1 - y_2| \]

我们称该函数满足在变量 \(y \in D \subset R^2\) 上的 Lipschitz 条件。

定理

假设 \(D = \{(t, y)\ |\ a \le t \le b, -\infty < y < \infty\}\)，且 \(f(t, y)\) 在 \(D\) 上连续。若 \(f\) 满足在变量 \(y \in D\) 上的 Lipschitz 条件，那么初值问题

\[ y'(t) = f(t, y), a \le t \le b, y(a) = \alpha \]

有唯一解 \(y(t)\)（\(a \le t \le b\)）。

定义

若初值问题

\[ y'(t) = f(t, y), a \le t \le b, y(a) = \alpha \]

满足以下条件，我们称之为适定性问题(well-posed problem)：

问题存在唯一解 \(y(t)\)
\(\forall \varepsilon > 0\)，存在正常数 \(k(\varepsilon)\)，使得当 \(|\varepsilon_0| < \varepsilon\)，并且 \(\delta(t)\) 在 \([a, b]\) 上连续且 \(|\delta(t)| < \varepsilon\) 时，对于

\[ z'(t) = f(t, z) + \delta(t), a \le t \le b, z(a) = \alpha + \varepsilon_0 \]

（上述式子称为扰动问题 (perturbed problem)），存在唯一解 \(z(t)\)，满足 \(|z(t) - y(t)| < k(\varepsilon) \cdot \varepsilon\ (a \le t \le b)\)

定理

假设 \(D = \{(t, y)\ |\ a \le t \le b, -\infty < y < \infty\}\)，且 \(f(t, y)\) 在 \(D\) 上连续。若 \(f\) 满足在变量 \(y \in D\) 上的 Lipschitz 条件，那么初值问题

\[ y'(t) = f(t, y), a \le t \le b, y(a) = \alpha \]

具有适定性 (well-posed)。

Euler's Method⚓︎

此处可以回顾前面提出的目标。

\(y'(t_0) \approx \dfrac{y(t_0 + h) - y(t_0)}{h}\ \Rightarrow\ y(t_1) \approx y(t_0) + hy'(t_0) = \alpha + hf(t_0, \alpha)\)

差分方程(difference equations)：\(\begin{cases}w_0 = \alpha \\ w_{i+1} = w_i + hf(t_i, w_i)\end{cases}\ (i = 0, \dots, n - 1)\)

定理

假设 \(f\) 是连续的，且满足 Lipschitz 条件，其常数 \(L \in D = \{(t, y)\ |\ a \le t \le b, -\infty < y < \infty \}\)；且存在常数 \(M, \forall\ a \le t \le b\)，满足 \(|y''(t)| \le M\)。

令 \(y(t)\) 为初值问题 \(y'(t) = f(t, y), a \le t \le b, y(a) = \alpha\) 的唯一解，且 \(w_0, w_1, \dots, w_n\) 为通过欧拉法（对于某些正整数 \(n\)）得到的近似值，那么：

\[ |y_i - w_i| \le \dfrac{hM}{2L}[e^{L(t_i - a)} - 1] \quad (i = 0, 1, \dots, n) \]

注

\(y''(t)\) 可在不知道 \(y(t)\) 的情况下被计算出来：

\[ y''(t) = \dfrac{d}{dt}y'(t) = \dfrac{d}{dt}f(t, y(t)) = \dfrac{\partial}{\partial t}f(t, y(t)) + \dfrac{\partial}{\partial y}f(t, y(t)) \cdot f(t, y(t)) \]

代入舍入误差后，差分方程为：\(\begin{cases}w_0 = \alpha \textcolor{red}{+ \delta_0} \\ w_{i+1} = w_i + hf(t_i, w_i) \textcolor{red}{+ \delta_{i+1}}\end{cases}(i = 0, \dots, n - 1)\)

定理

令 \(y(t)\) 为初值问题 \(y'(t) = f(t, y), a \le t \le b, y(a) = \alpha\) 的唯一解，且 \(w_0, w_1, \dots, w_n\) 为使用上述差分方程得到的近似值。若 \(|\delta_i| < \delta\ (i = 0, \dots, n)\)，那么 \(\forall\ i\)

\[ |y_i - w_i| \le \dfrac{1}{L} \Big(\dfrac{hM}{2} + \dfrac{\delta}{h}\Big)[e^{L(t_i - a)} - 1] + |\delta_0|e^{L(t_i - a)} \]

其中 \(h \ge \sqrt{2 \delta / M}\)

High Order Taylor Methods⚓︎

定义

差分法 \(\begin{cases}w_0 = \alpha \\ w_{i+1} = w_i + h\varphi(t_i, w_i)\end{cases} (i = 0, \dots, n - 1)\) 的局部截断误差(local truncation error) 为：

\[ \tau_{i+1}(h) = \dfrac{y_{i+1} - (y_i + h\varphi(t_i, y_i))}{h} = \dfrac{y_{i+1} - y_i}{h} - \varphi(t_i, y_i) \quad (i = 0, \dots, n - 1) \]

注

局部截断误差就是 \(\dfrac{y_{i+1} - w_{i+1}}{h}\)（基于假设 \(w_i = y_i\)）。

欧拉法的局部截断误差：

\[ \begin{align} \tau_{i+1} & = \dfrac{y_{i+1} - w_{i+1}}{h} = \dfrac{[y_i + hy'(t_i) + \frac{h^2}{2}y''(\xi_i)] - [y_i + hf(t_i, y_i)]}{h} \notag \\ & = \dfrac{h}{2} y''(\xi_i) = O(h) \notag \end{align} \]

所以欧拉法的阶数为 1

注

可通过 \(n = 1\) 时泰勒展开式得到的欧拉法近似表示 \(y(t)\)。

高阶泰勒法公式为：

\[ y_{i+1} = y_i + hf(t_i, y_i) + \dfrac{h^2}{2} f'(t_i, y_i) + \dots + \dfrac{h^n}{n!}f^{(n-1)}(t_i, y_i) + \dfrac{h^{(n+1)}}{(n+1)!}f^{(n)}(\xi_i, y(\xi_i)) \]

对于阶数为 \(n\) 的泰勒法，其对应的差分方程为：

\[ \begin{cases}w_0 = \alpha \\ w_{i+1} = w_i + hT^{(n)}(t_i, w_i)\end{cases} (i = 0, \dots, n - 1) \]

其中 \(T^{(n)}(t_i, w_i) = f(t_i, w_i) + \dfrac{h}{2}f'(t_i, w_i) + \dots + \dfrac{h^{n-1}}{n!} f^{(n-1)}(t_i, w_i)\)

若 \(y \in C^{n+1}[a, b]\)，那么局部截断误差是 \(O(h^n)\)。

讨论

题目解答

应用 \(n = 10\) 的 3 阶泰勒法，解决初值问题 \(y' = y - t^2 + 1, 0 \le t \le 2, y(0) = 0.5\)。

找到 \(f\) 的前两个导数：

\(f(t, y(t)) = y(t) - t^2 + 1\)
\(f'(t, y(t)) = y'(t) - 2t = y(t) - t^2 + 1 - 2t\)
\(f''(t, y(t)) = y'(t) - 2t - 2 = y(t) - t^2 - 2t - 1\)

得到：

\[ \begin{align} T^{(3)}(t_i, w_i) & = f(t_i, w_i) + \dfrac{h}{2} f'(t_i, w_i) + \dfrac{h^2}{6}f''(t_i, w_i) \notag \\ & = \Big(1 + \dfrac{h}{2} + \dfrac{h^2}{6} \Big)(w_i - t_i^2 + 1) - \Big(1 + \dfrac{h}{3}\Big)ht_i - \dfrac{h^2}{3} \notag \end{align} \]

通过 3 阶泰勒法，得到差分方程：\(\begin{cases}w_0 = 0.5 \\ w_{i+1} = w_i + h\Big[\Big(1 + \dfrac{h}{2} + \dfrac{h^2}{6}\Big)(w_i - t_i^2 + 1) - \Big(1 + \dfrac{h}{3}ht_i - \dfrac{h^2}{3}\Big)\Big]\end{cases}\)

因为 \(n = 10\)，那么 \(h = 0.2, t_i = 0.2i, w_{i+1} = 1.22133w_i - 0.00855i^2 - 0.00853i + 0.21867\)。

Other Euler's Methods⚓︎

隐式欧拉法(implicit Euler's method)
- \(y'(t_0) \approx \dfrac{y(t_0) - y(t_0 - h)}{h}\ \Rightarrow\ \textcolor{red}{y(t_1)} \approx y(t_0) + hy'(t_1) + \alpha + hf(t_1, \textcolor{red}{y(t_1)})\)
- 差分方程为 \(\begin{cases}w_0 = \alpha \\ \textcolor{red}{w_{i+1}} = w_i + hf(t_{i+1}, \textcolor{red}{w_{i+1}})\end{cases} (i = 0, \dots, n - 1)\)
- 通常以迭代形式求解 \(w_{i+1}\)，其初始值通过显式法给出
- 隐式欧拉法的局部截断误差为 \(\tau_{i+1} = \dfrac{y_{i+1} - w{i+1}}{h} = -\dfrac{h}{2}y''(\xi_i) = O(h)\)
梯形法(trapezoidal method)
- 差分方程为 \(\begin{cases}w_0 = \alpha \\ \textcolor{red}{w_{i+1}} = w_i + \dfrac{h}{2}[f(t_i, w_i) + f(t_{i+1}, \textcolor{red}{w_{i+1}})]\end{cases} (i = 0, \dots, n - 1)\)
- 注：局部截断误差为 \(O(h^2)\)；但必须以迭代方式求解隐式方程。
两步法(double-step method)
- \(y'(t_0) = \dfrac{1}{2h}[y(t_0 + h) - y(t_0 - h)] - \dfrac{h^2}{6}y^{(3)}(\xi_1)\ \Rightarrow\ y(t_2) \approx y(t_0) + 2hf(t_1, y(t_1))\)
- 差分方程为 \(\begin{cases}w_0 = \alpha \\ w_{i+1} = w_{i-1} + 2hf(t_i, w_i)\end{cases} (i = 1, \dots, n - 1)\)
- 该方法要求两个初始点向前移动，故得其名；而先前讨论的方法都是单步法(single-step methods)。
- 若假设 \(w_{i-1} = y_{i-1}, w_i = y_i\)，那么局部截断误差为 \(O(h^2)\)

!!! abstract " 比较上述各法的优劣

|方法|👍|👎|
|:-:|:-:|:-:|
|欧拉显式法|简单|低阶精度|
|欧拉隐式法|稳定|低阶精度、耗时|
|梯形法|更精确|耗时|
|两步法|更精确、显式|要求一个额外的初始点|

Runge-Kutta Methods⚓︎

Runge-Kutta 法是一种具有高阶局部截断误差的单步方法，无需计算 \(f\) 的导数。

思路：在这样的单步方法中，我们考虑一条在点 \((t_i, w_i), (t_{i+1}, w_{i+1})\) 之间的线段的斜率。我们可以通过找到更好的斜率来改善结果。

观察欧拉法：

\[ \begin{cases} w_{i+1} & = w_i + h\Big[ \dfrac{1}{2} K_1 + \dfrac{1}{2} K_2 \Big] \\ K_1 & = f(t_i, w_i) \\ K_2 & = f(t_i + h, w_i + hK_1) \end{cases} \]

斜率是否必须是 \(K_1, K_2\) 的平均值？
步幅是否必须为 \(h\)？

我们将其进一步泛化：

\[ \begin{cases} w_{i+1} & = w_i + h[\textcolor{red}{\lambda_1} K_1 + \textcolor{red}{\lambda_2} K_2 ] \\ K_1 & = f(t_i, w_i) \\ K_2 & = f(t_i + \textcolor{red}{p}h, w_i + \textcolor{red}{p}hK_1) \end{cases} \]

我们要找到 \(\lambda_1, \lambda_2, p\)，使得该方法的局部阶段误差的阶数为 2。

写出 \(K_2\) 在 \((t_i, y_i)\) 上的泰勒展开式：

\[ \begin{align} K_2 & = f(t_1 + ph, y_i + phK_1) \notag \\ & = f(t_i, y_i) + phf_t(t_i, y_i) + phK_1f_y(t_i, y_i) + O(h^2) \notag \\ & = y'(t_i) + phy''(t_i) + O(h^2) \notag \end{align} \]

注

\[ \begin{align} y''(t) & = \dfrac{d}{dt}f(t, y) \notag \\ & = f_t(t, y) + f_y(t, y) \dfrac{dy}{dt} \notag \\ & = f_t(t, y) + f_y(t, y)f(t, y) \notag \end{align} \]
将 \(K_2\) 代入到第一个式子中：

\[ \begin{align} w_{i+1} & = y_i + h\{\lambda_1 y'(t_i) + \lambda_2[y'(t_i) + phy''(t_i) + O(h^2)]\} \notag \\ & = y_i + (\lambda_1 + \lambda_2) hy'(t_i) + \lambda_2 ph^2 y''(t_i) + O(h^3) \notag \end{align} \]
找到 \(\lambda_1, \lambda_2, p\)，使得 \(\tau_{i+1} = (y_{i+1} - w_{i+1}) / h = O(h^2)\)

\[ \begin{align} w_{i+1} & = y_i + (\lambda_1 + \lambda_2) hy'(t_i) + \lambda_2 ph^2 y''(t_i) + O(h^3) \notag \\ y_{i+1} & = y_i + hy'(t_i) + \dfrac{h^2}{2} y''(t_i) + O(h^3) \notag \end{align} \]

可以得到：\(\lambda_1 + \lambda_2 = 1, \lambda_2 p = \dfrac{1}{2}\)（3 个未知数，2 个方程）

所以有无穷多个解。而由这两个方程得到的一系列方法被称为 2 阶 Runge-Kutta 法(Runge-Kutta method of order 2)。

注

修改后的欧拉法就是龙格 - 库塔法的一种特殊情况（\(p = 1, \lambda_1 = \lambda_2 = \dfrac{1}{2}\)）

其他方法

中点法(midpoint method)：将从二阶泰勒法中的 \(T^{(2)}(t, y)\) 用 \(f(t + h / 2, y + (h / 2)f(t, y))\) 替换得到的差分方程法。

\[ \begin{cases} w_0 = \alpha \\ w_{i+1} = w_i + hf(t_i + \dfrac{h}{2}, w_i + \dfrac{h}{2}f(t_i, w_i)) \end{cases} \quad (i = 0, \dots, N - 1) \]
改进欧拉法(modified Euler method)：

\[ \begin{cases} w_0 = \alpha \\ w_{i+1} = w_i + \dfrac{h}{2}[f(t_i, w_i) + f(t_{i+1}, w_i + hf(t_i, w_i))] \end{cases} \quad (i = 0, \dots, N - 1) \]
Heun 法：

\[ \begin{cases} w_0 = \alpha \\ w_{i+1} = w_i + \dfrac{h}{4}[f(t_i, w_i) + 3f(t_i + \dfrac{2}{3}h, w_i + \dfrac{2}{3}hf(t_i, w_i))] \end{cases} \quad (i = 0, \dots, N - 1) \]

计算更高精度：

\[ \begin{cases} w_{i+1} & = y_i + h[\textcolor{red}{\lambda_1} K_1 + \textcolor{red}{\lambda_2} K_2 + \dots + \textcolor{red}{\lambda_m} K_m] \\ K_1 & = f(t_i, w_i) \\ K_2 & = f(t_i + \textcolor{red}{\alpha_2} h, w_i + \textcolor{red}{\beta_{21}} hK_1) \\ K_3 & = f(t_i + \textcolor{red}{\alpha_3} h, w_i + \textcolor{red}{\beta_{31}} hK_1 + \textcolor{red}{\beta_{32}} hK_2) \\ \dots \\ K_m & = f(t_i + \textcolor{red}{\alpha_m} h, w_i + \textcolor{red}{\beta_{m1}} hK_1 + \textcolor{red}{\beta_{m2}} hK_2 + \dots + \textcolor{red}{\beta_{m, m-1}} hK_{m-1}) \\ \end{cases} \]

最流行的是经典 4 阶 Runge-Kutta 法：

\[ \begin{cases} w_{i+1} = w_i + \dfrac{h}{6}(K_1 + 2K_2 + 2K_3 + K_4) \\ K_1 = f(t_i, w_i) \\ K_2 = f(t_i + \dfrac{h}{2}, w_i + \dfrac{h}{2} K_1) \\ K_3 = f(t_i + \dfrac{h}{2}, w_i + \dfrac{h}{2} K_2) \\ K_4 = f(t_i + h, w_i + hK_3) \end{cases} \]

注

在使用 Runge-KUtta 法时，主要的计算量在于求解 \(f\)。Butcher 已经帮我们建立好了每步求值次数与局部截断误差阶数之间的关系：

每步求值次数 2 3 4 5-7 8-9 n≥10

最佳可能的 LTE \(O(h^2)\) \(O(h^3)\) \(O(h^4)\) \(O(h^{n-1})\) \(O(h^{n-2})\) \(O(h^{n-3})\)
因为 Runge-Kutta 法时基于泰勒展开式的，所以 \(y\) 不得不足够平滑，以获取在高阶方法下的更高的精度。通常低阶方法相比高阶方法会采用更小的步幅。

Multistep Methods⚓︎

思路：使用 \(y, y'\) 在多个网格点 (mesh points) 上的线性组合，以得到更好的近似值 \(y(t_{i+1})\)。

多步法(multistep method) 的一般形式如下：

\[ w_{i+1} = \textcolor{red}{a_{m-1}} w_i + \textcolor{red}{a_{m-2}} w_{i-1} + \dots + \textcolor{red}{a_0} w_{i+1-m} + h[\textcolor{red}{b_m} f_{i+1} + \textcolor{red}{b_{m-1}} f_i + \dots + \textcolor{red}{b_0} f_{i+1-m}] \]

在隐式法中，\(b_m \ne 0\)
在显式法中，\(b_m = 0\)

具体方法：从积分中获取。在 \([t_i, t_{i+1}]\) 上对 \(y'(t) = f(t, y)\) 进行积分，得到：

\[ y(t_{i+1}) - y(t_i) = \int_{t_i}^{t_{i+1}} f(t, y(t)) dt \]

关键是近似计算积分。不同的近似方法会得到不同的差分方程。

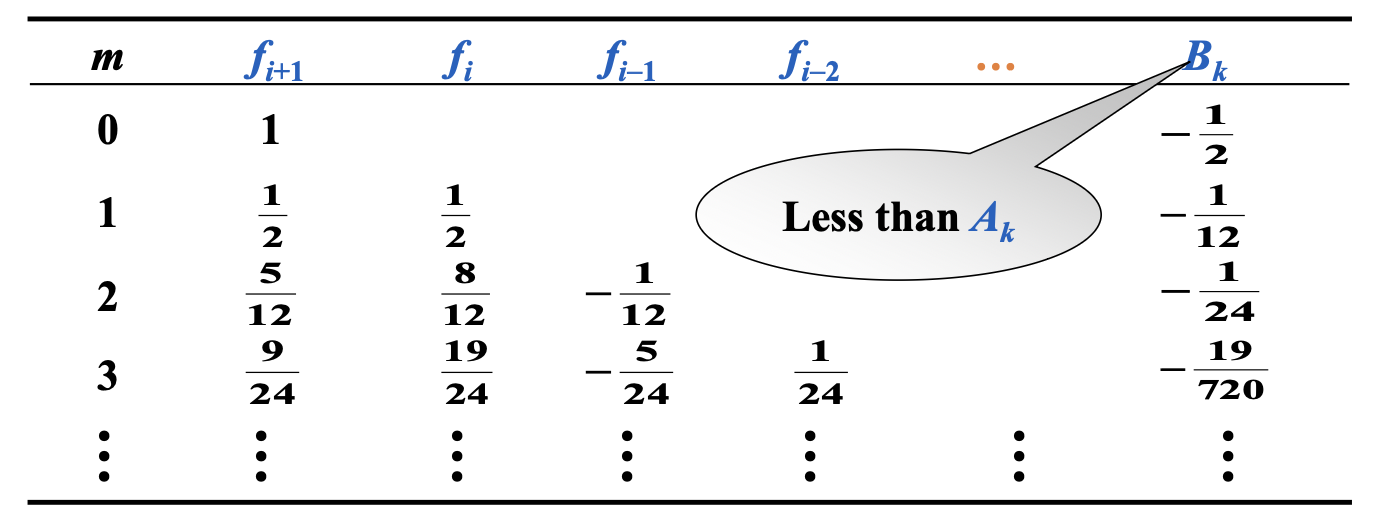
Adams-Bashforth Explicit \(m\)-step Technique⚓︎

使用牛顿后向差分公式，在 \((t_i, f_i), (t_{i-1}, f_{i-1}), \dots, (t_{i+1-m}, f_{i+1-m})\) 上对 \(f\) 进行插值，并得到 \(P_{m-1}(t)\)。或者令 \(t = t_i + sh, s \in [0, 1]\)，我们有：

\[ \int_{t_i}^{t_{i+1}} f(t, y(t)) dt = h \int_0^1 P_{m-1}(t_i + sh) ds + h \int_0^1 \underbrace{R_{m-1}}_{\substack{\text{local} \\ \text{truncation} \\ \text{error}}}(t_i + sh) ds \]

最后得到显式公式：\(w_{i+1} = w_i + h\int_0^1 P_{m-1}(t_i + sh)ds\)

定义

多步法的局部截断误差为：

\[ \tau_{i+1}(h) = \dfrac{y_{i+1} - (a_{m-1}y_i + \dots + a_0 y_{i+1-m})}{h} - [b_m f_{i+1} + \dots + b_0 f_{i+1-m}] \]

其中 \(i = m-1, m, \dots, n - 1\)

例子

题目解答

请求出 Adams-Bashforth 2 步显式法。

使用牛顿后向差分公式，在 \((t_i, f_i), (t_{i-1}, f_{i-1})\) 上对 \(f\) 插值：

\[ P_1(t_i + sh) = f_i + s \nabla f_i = f_i + s(f_i - f_{i-1}) \]

得到 \(w_{i+1} = w_i + h \int_0^1 [f_i + s(f_i - f_{i-1})] ds = w_i + \dfrac{h}{2} (3f_i - f_{i-1})\)

局部截断误差为：

\[ \begin{align} \tau_{i+1} & = \dfrac{y(t_{i+1}) - w_{i+1}}{h} = \int_0^1 R_1 (t_i + sh) ds \notag \\ & = \int_0^1 \dfrac{d^2 f(\xi_i, t(\xi_i))}{dt^2} \dfrac{1}{2!} sh(s+1)h ds = \dfrac{5}{12} h^2 y'''(\widetilde{\xi_i}) \notag \end{align} \]

注

一般来说，对于 \(\tau = A_mh^my^{(m+1)}(\xi_i)\)，\(A_m\) 和系数 \(f_i, f_{i-1}, f_{i+1-m}\) 能从表格中找到。

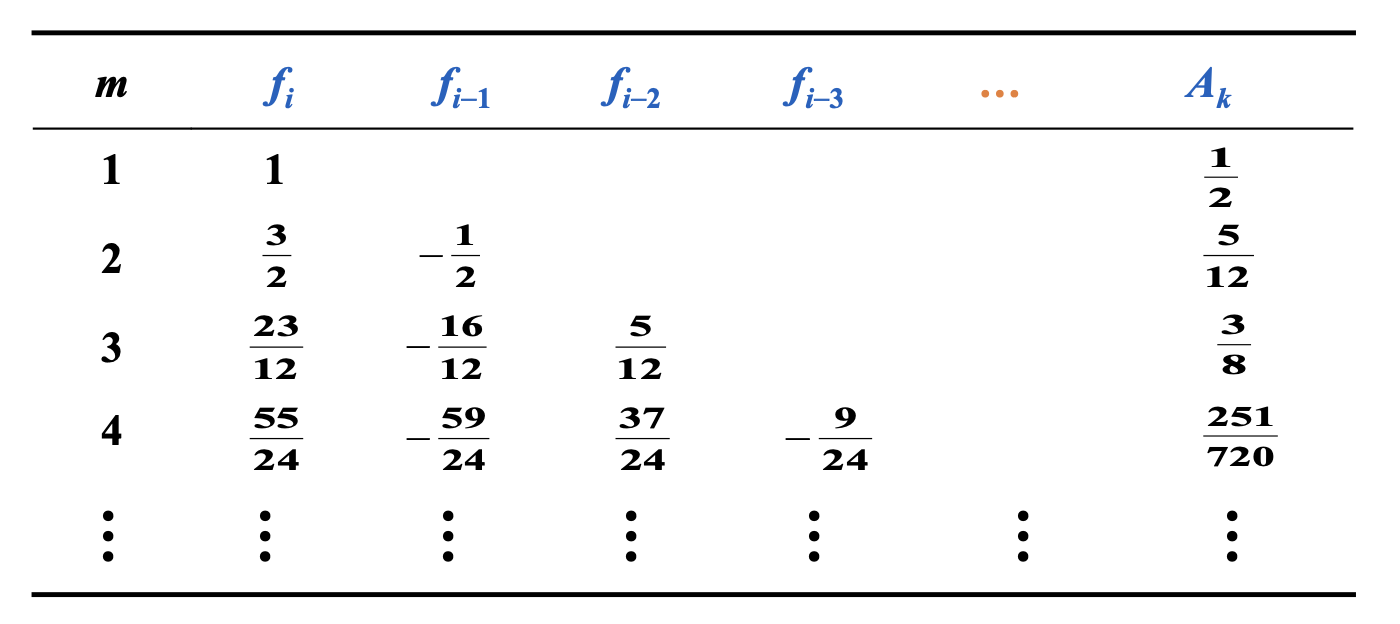
Adams-Bashforth 4 步显式法：\(w_{i+1} = w_i + \dfrac{5}{24} (55f_i - 59 f_{i-1} + 37 f_{i-2} - 9f_{i-3})\)

Adams-Moulton Implicit \(m\)-step Technique⚓︎

使用牛顿前向差分公式，在 \((t_{i+1}, \textcolor{red}{f_{i+1}}), (t_i, f_i), \dots, (t_{i+1-m}, f_{i+1-m})\) 上对 \(f\) 进行插值，并得到 \(P_m(t)\)。类似的，我们可以得到一组 \(\tau_{i+1} = B_m h^{m+1} y^{(m+2)} (\xi_i)\) 的隐式公式。

Adams-Moulton 3 步隐式法：\(w_{i+1} = w_i + \dfrac{h}{24} (9 f_{i+1} + 19 f_i - 5 f_{i-1} + f_{i-2})\)

Adams Predictor-Corrector System⚓︎

用Runge-Kutta 法计算前 \(m\) 个初始值
用 Adams-Bashforth 显式法进行预测
用 Adams-Moulton 隐式法进行校正

注

对于上述步骤用到的三个公式，它们的局部截断误差必须有相同的阶数。
最受欢迎的系统是将 4 阶 Adams-Bashforth 法作为预测器，将 1 次迭代下的 Adams-Moulton 法作为校正器，而起始值通过 4 阶 Runge-Kutta 法获得。

Derive from Taylor Expansion⚓︎

\[ w_{i+1} = \textcolor{red}{a_{m-1}}w_i + \textcolor{red}{a_{m-2}}w_{i-1} + \dots + \textcolor{red}{a_0}w_{i+1-m} + h[\textcolor{red}{b_{m}}f_{i+1} + \textcolor{red}{b_{m-1}}f_i + \dots + \textcolor{red}{b_0}f_{i+1-m}] \]

思路：扩展在关于 \(t_i\) 的泰勒级数里的 \(y_{i-1}, \dots, y_{i+1-m}\) 和 \(f_{i+1}, f_{i-1}, \dots, f_{i+1-m}\)，并让 \(h^k\) 的系数相等，以获得 \(a_0, \dots, a_{m-1}\) 和 \(b_0, \dots, b_m\)。

例子

题目解答

请求出形如以下形式的 4 阶公式：

\[ w_{i+1} = \textcolor{red}{a_2}w_i + \textcolor{red}{a_1}w_{i-1} + \textcolor{red}{a_0}w_{i-2} + h[\textcolor{red}{b_3}f_i + \textcolor{red}{b_2}f_{i-1} + \textcolor{red}{b_1}f_{i-2} + \textcolor{red}{b_0}f_{i-3}] \]

在 \(t_i\) 处扩展 \(y_{i-1}, y_{i-2}, f_{i-1}, f_{i-2}, f_{i-3}\) 和 \(y(t_{i+1})\)

假设 \(w_i = y_i\) 的情况下，\(\tau_{i+1} = \dfrac{y_{i+1} - w_{i+1}}{h} = O(h^4)\)

\[ \begin{align} y_{i-1} = & y_i - hy_i' + \dfrac{1}{2} h^2 y_i'' - \dfrac{1}{6}h^3 y_i''' + \dfrac{1}{24}h^4 y_i^{(4)} + O(h^5) \notag \\ y_{i-2} = & y_i - 2hy_i' + 2 h^2 y_i'' - \dfrac{4}{3}h^3 y_i''' + \dfrac{2}{3}h^4 y_i^{(4)} + O(h^5) \notag \\ f_{i-1} = & y_i' - hy_i'' + \dfrac{1}{2}h^2 y_i''' - \dfrac{1}{6}h^3y_i^{(4)} + O(h^4) \notag \\ f_{i-2} = & y_i' - 2hy_i'' + 2h^2 y_i''' - \dfrac{4}{3}h^3y_i^{(4)} + O(h^4) \notag \\ f_{i-3} = & y_i' - 3hy_i'' + \dfrac{9}{2}h^2 y_i''' - \dfrac{9}{2}h^3y_i^{(4)} + O(h^4) \notag \\ \end{align} \]

\[ y(t_{i+1}) = y_i + hy_i' + \dfrac{1}{2}h^2y_i'' + \dfrac{1}{6}h^3 y_i''' + \dfrac{1}{24}h^4 y_i^{(4)} + O(h^5) \]

有 5 个方程，7 个未知量。

令 \(a_0 = a_1 = 0\) -> Adams-Bashforth 显式法
用 \(f_{i+1}\) 替换 \(f_{i-1}\)，并令 \(a_0 = a_1 = 0\) -> Adams-Bashforth 隐式法
用 \(w_{i-3}\) 替换 \(f_{i-3}\)，我们能得到另一组阶数为 4 的方法，包括了显式 Milne 法：

\[ w_{i+1} = w_{i-3} + \dfrac{4h}{3}(2f_i - f_{i-1} + 2f_{i-2}) \]

其截断误差为 \(\dfrac{14}{45}h^4y^{(5)}(\xi_i), \xi_i \in (t_{i-3}, t_{i+1})\)
令 \(a_0 = 0, a_1 = 1\) -> Simpson 隐式法

\[ w_{i+1} = w_{i-1} + \dfrac{h}{3}(f_{i+1} + 4f_i + f_{i-1}) \]

其截断误差为 \(-\dfrac{h^4}{90}y^{(5)}(\xi_i), \xi_i \in (t_{i-1}, t_{i+1})\)

Higher-Order Equations and Systems of Differential Equations⚓︎

m-th Order System of 1st-Order IVP⚓︎

\[ \begin{cases} u_1'(t) = f_1(t, u_1(t), \dots, u_m(t)) \\ \dots \\ u_m'(t) = f_m(t, u_1(t), \dots, u_m(t)) \end{cases} \]

初始条件为：\(u_1(a) = \alpha_1, u_2(a) = \alpha_2, \dots, u_m(a) = \alpha_m\)

令 \(\bm{y} = \begin{bmatrix}u_1 \\ \vdots \\ u_m\end{bmatrix}, \bm{f} = \begin{bmatrix}f_1 \\ \vdots \\ f_m\end{bmatrix}, \bm{\alpha} = \begin{bmatrix}\alpha_1 \\ \vdots \\ \alpha_m\end{bmatrix}\)，可以得到：\(\begin{cases}\bm{y}'(t) = \bm{f}(t, \bm{y}) \\ \bm{y}(a) = \bm{\alpha}\end{cases}\)

Higher-Order Differential Equation⚓︎

\[ \begin{cases} y^{(m)}(t) = f(t, y, y', \dots, y^{(m-1)}), a \le t \le b \\ y(a) = \alpha_1, y'(a) = \alpha_2, \dots, y^{(m-1)}(a) = \alpha_m \end{cases} \]

思路：将高阶的微分方程归约到一个 1 阶的微分方程组。

令 \(u_1(t) = y(t), u_2(t) = y'(t), \dots, u_m(t) = y^{(m-1)}(t)\)，得到：

\[ \begin{cases} u_1' = y' = u_2 \\ u_2' = y'' = u_3 \\ \vdots \\ u_{m-1}' = y^{(m-1)} = u_m \\ u_m' = y^{(m)} = f(x, u_1, \dots, u_m) \end{cases} \]

初始条件为 \(u_1(a) = \alpha_1, u_2(a) = \alpha_2, \dots, u_m(a) = \alpha_m\)。

例子

题目解答

使用欧拉法求解以下 IVP（\(h = 0.1\)）

\[ \begin{align} & y'' - 2y' + y = te^t - 1.5t + 1 \quad \text{for } 0 \le t \le 0.2 \notag \\ & y(0) = 0, y'(0) = -0.5 \notag \end{align} \]

令 \(u_1(t) = y(t), u_2(t) = y'(t)\)，得到：

\[ \begin{cases} u_1'(t) = u_2(t) \\ u_2'(t) = te^t - 1.5t + 1 - u_1(t) + 2u_2(t) \end{cases} \]

初始条件为 \(u_1(0) = 0, u_2(0) = -0.5\)

根据

\[ \begin{align} w_{i+1} & = w_1 + h\Big[\dfrac{1}{2}K_1 + \dfrac{1}{2}K_2\Big] \notag \\ K_1 & = f(t_i, w_i) \notag \\ K_2 & = f(t_i + h, w_i + hK_1) \notag \end{align} \]

，计算：

精确解为：\(y(t) = \dfrac{t^3 e^t}{6} - te^t + 2e^t - 1.5t - 2\)

Stability⚓︎

定义

当局部截断误差为 \(\tau_i(h)\) 的一步微分方程法满足下面的条件时，我们认为它和近似得到的微分方程是一致的(consistent)：

\[ \lim\limits_{h \rightarrow 0} \max\limits_{1 \le i \le n} |\tau_i(h)| = 0 \]

对于多步法，还要求对于 \(i = 1, 2, \dots, m-1\)，有 \(\lim\limits_{h \rightarrow 0}|w_i - y_i| = 0\)

定义

当满足下面的条件时，我们认为一步微分方程法关于近似得到的微分方程收敛(convergent)：

\[ \lim\limits_{h \rightarrow 0} \max\limits_{1 \le i \le n} |w_i - y_i| = 0 \]

多步法和上面的一样。

定义

若在初始条件中的小改变或小扰动产生对应较小的近似值变化，那么称该方法是稳定的(stable)。

讨论

题目解答

使用欧拉显式法和隐式法，以及改进欧拉法解决以下初值问题：\(y'(t) = -30y(t), y(0) = 1\)，区间为 \([0, 0.5], h = 0.1\)。

定义

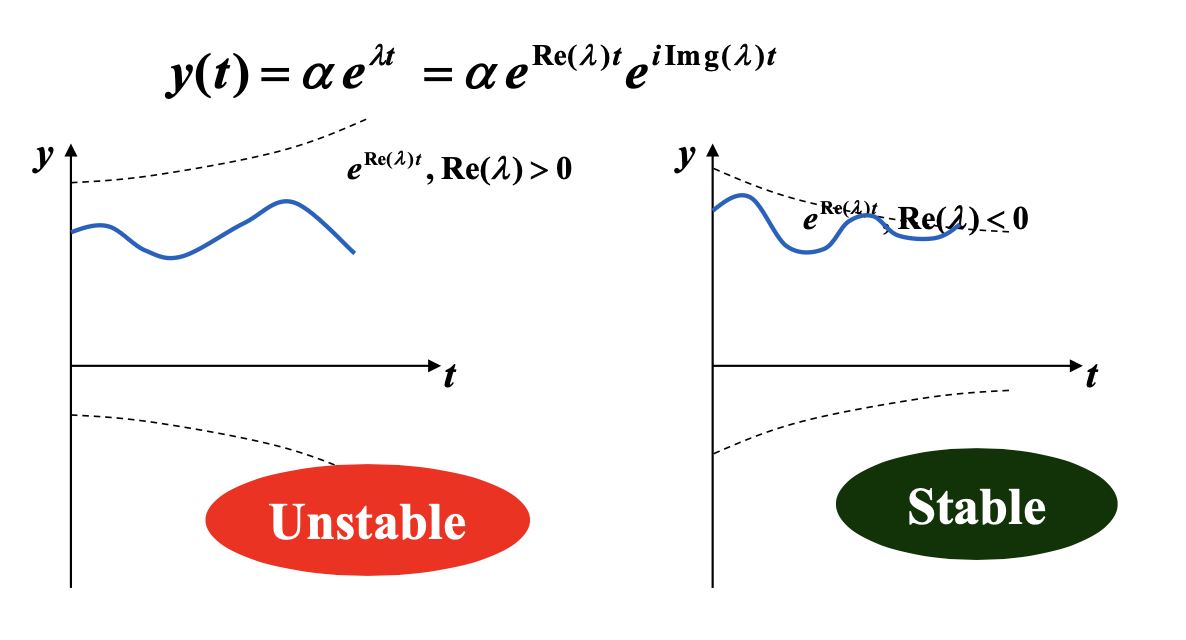
将某个方法用在一个简单的检验方程(test equation) 上：\(y' = \lambda y, y(0) = \alpha\)，其中 \(\text{Re}(\lambda) < 0\)。假设摄入误差仅在初始点被引入。如果这个初始误差在特定步幅 \(h\) 上被缩小的话，那么该方法关于 \(H = \lambda h\) 是绝对稳定的(absolutely stable)。所有 \(H\) 构成的集合称为绝对稳定性区域(the region of absolute stability)。

当 \(A\) 的绝对稳定性区域大于 \(B\) 时，称法 \(A\) 比法 \(B\) 更稳定。

例子

例 1 例 2 例 3 例 4

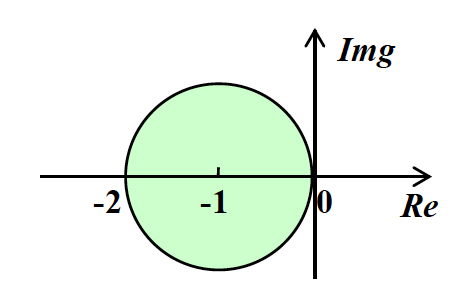
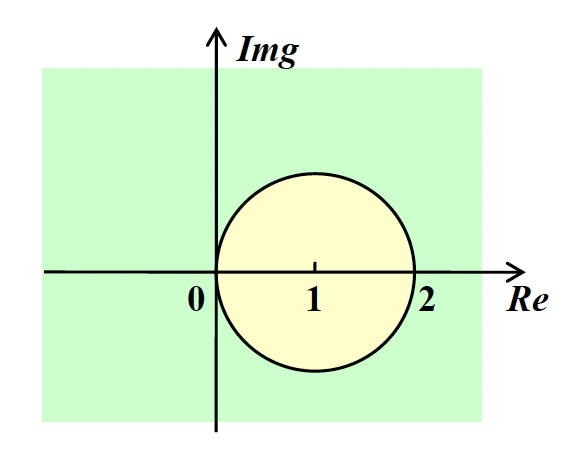
考虑欧拉显式法 \(w_{i+1} = w_i + hf_i\)

\[ w_{i+1} = w_i + h\lambda w_i = \alpha(1 + H)^{i+1} \]

\[ \alpha^* = \alpha + \varepsilon \Rightarrow w_{i+1}^* = \alpha^* (1 + H)^{i+1} \Rightarrow \varepsilon_{i+1} = w_{i+1}^* - w_{i+1} = (1 + H)^{i + 1}\varepsilon \]

因此要想保证误差减小，必须满足 \(|1 + H| < 1\)。

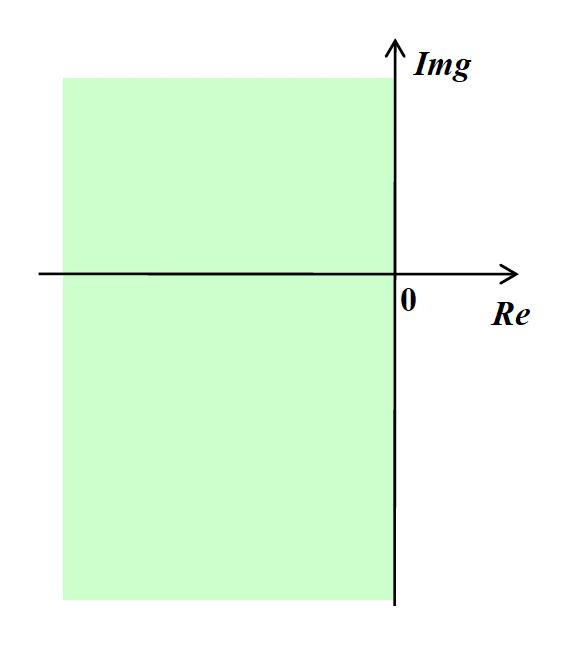
考虑欧拉隐式法 \(w_{i+1} = w_i + hf_{i+1}\)

\[ w_{i+1} = \Big(\dfrac{1}{1 - H}\Big)w_i \Rightarrow \varepsilon_{i+1} = \Big(\dfrac{1}{1 - H}\Big)^{i+1} \varepsilon \]

因此要想保证误差减小，必须满足 \(|1 - H| < 1\)。

注

它是无条件稳定的(unconditionally stable)。

考虑 2 阶 Runge-Kutta 隐式法：

\[ \begin{cases} w_{i+1} = w_i + hK_1 \\ K_1 = f(t_i + \dfrac{h}{2}, w_i + \dfrac{h}{2}K_1) \end{cases} \]

可以得到 \(K_1 = \dfrac{\lambda w_i}{1 - \frac{\lambda h}{2}} \Rightarrow w_{i+1} = \Big(\dfrac{2+H}{2-H}\Big)w_i \Rightarrow \Big|\dfrac{2+H}{2-H}\Big| < 1\)

注

它是无条件稳定的(unconditionally stable)。

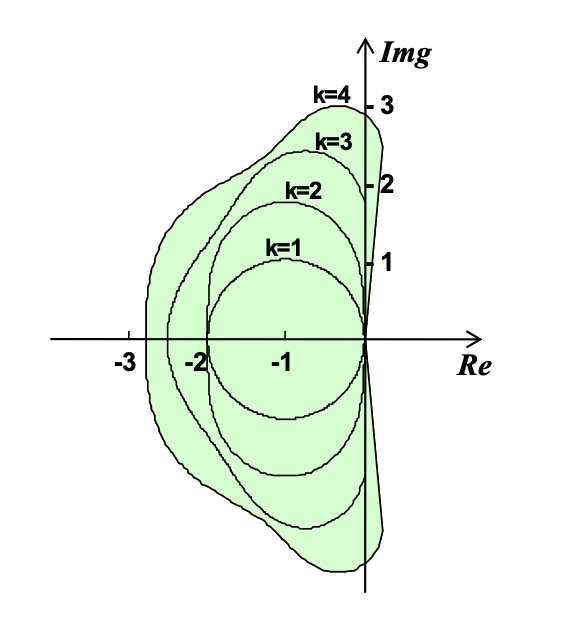
补充：1-4 阶的 Runge-Kutta 显式法

\[ \begin{cases} w_{i+1} & = w_i + \dfrac{h}{6} (K_1 + 2K_2 + 2K_3 + 2K_4) \\ K_1 & = f(t_i, w_i) \\ K_2 & = f(t_i + \dfrac{h}{2}, w_i + \dfrac{h}{2} K_1) \\ K_3 & = f(t_i + \dfrac{h}{2}, w_i + \dfrac{h}{2} K_2) \\ K_4 & = f(t_i + h, w_i + \dfrac{h}{2} K_3) \\ \end{cases} \]

\[ \begin{align} K_1 & = \lambda w_i \notag \\ K_2 & = \lambda w_i (1 + \dfrac{H}{2}) \notag \\ K_3 & = \lambda w_i (1 + \dfrac{H}{2} + \dfrac{H^2}{4}) \notag \\ K_4 & = \lambda w_i (1 + H + \dfrac{H^2}{2} + \dfrac{H^3}{4}) \notag \\ w_{i+1} & = w_i \Big(1 + H + \dfrac{H^2}{2} + \dfrac{H^3}{6} + \dfrac{H^4}{24}\Big) \end{align} \]

题目解答

考虑以下 IVP 组（刚性组 (stiff system)）：

\[ \begin{cases} u_1' & = 9u_1 + 24u_2 + 5 \cos t - \dfrac{1}{3} \sin t, \quad u_1(0) = \dfrac{4}{3} \\ u_2' & = -24u_1 - 51u_2 - 9 \cos t + \dfrac{1}{3} \sin t, \quad u_1(0) = \dfrac{2}{3} \end{cases} \]

如何选择步幅 \(h\)，以保证应用欧拉显式法之后的稳定性？

唯一解为：\(\begin{cases}u_1(t) = 2e^{-3t} - e^{-39t} + \dfrac{1}{3} \cos t \\ u_2(t) = -e^{-3t} + 2e^{-39t} - \dfrac{1}{3} \cos t\end{cases}\)。

矩阵 \(\begin{bmatrix}9 & 24 \\ -24 & 51\end{bmatrix}\) 的特征值为 \(\lambda_1 = -3, \lambda_2 = -39\)

\(-2 < \lambda h < 0 \Rightarrow h < \dfrac{2}{39} \approx 0.051\)

对应的作业练习📝

评论区

如果大家有什么问题或想法，欢迎在下方留言~