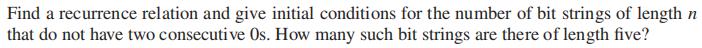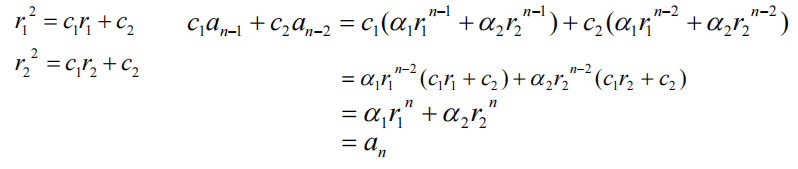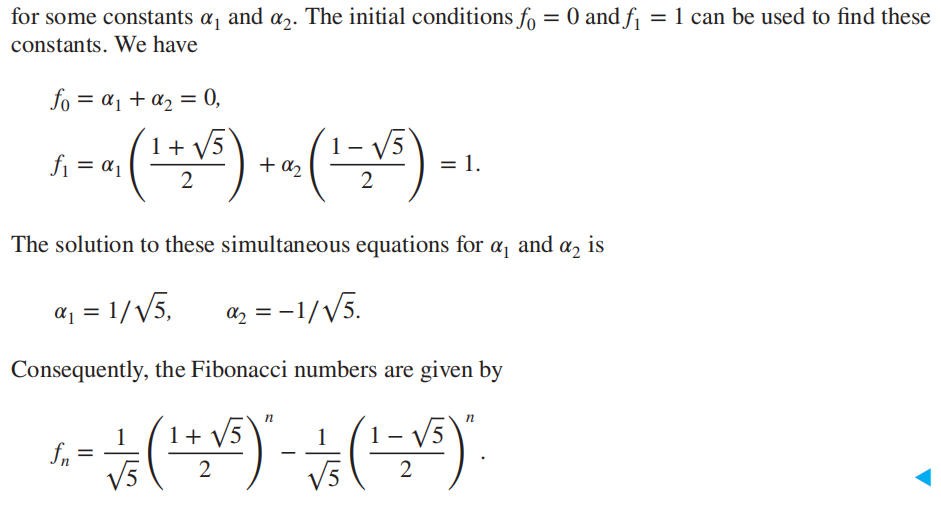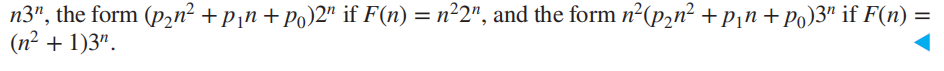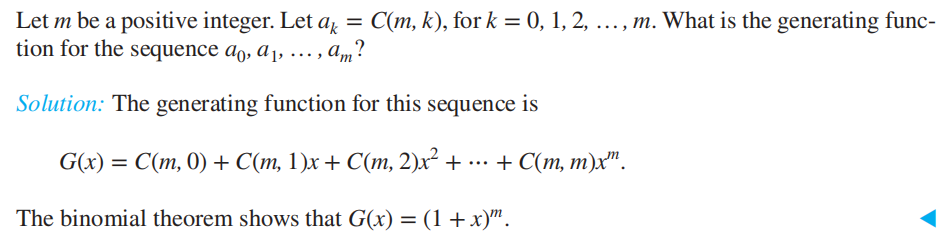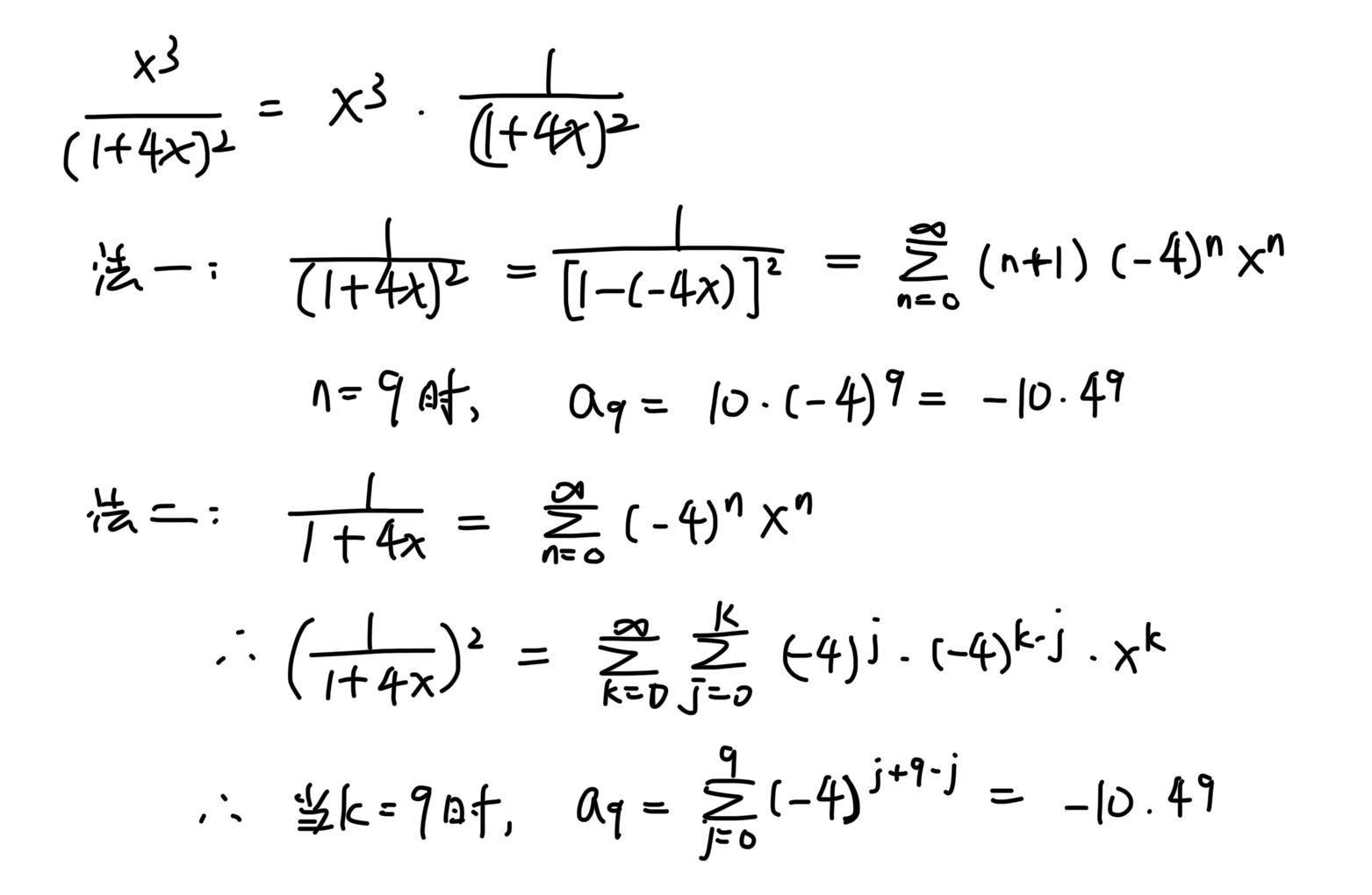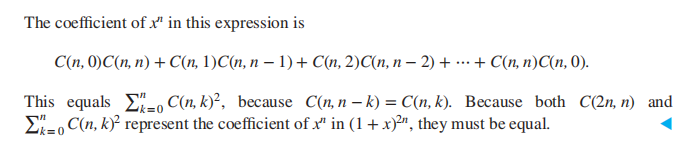Chap 8 Advanced Counting Techniques⚓︎

约 5913 个字预计阅读时间 30 分钟

核心知识

求解线性齐次 / 非齐次递推关系
生成函数：计数、求解递推关系 ...
容斥原理（的推广）
- 计算满射函数的个数
- 错排

Applications of Recurrence Relations⚓︎

Modelling with Recurrence Relations⚓︎

回顾：

递归定义
递推关系
递推关系的解 (solution)：满足递推关系的某个序列

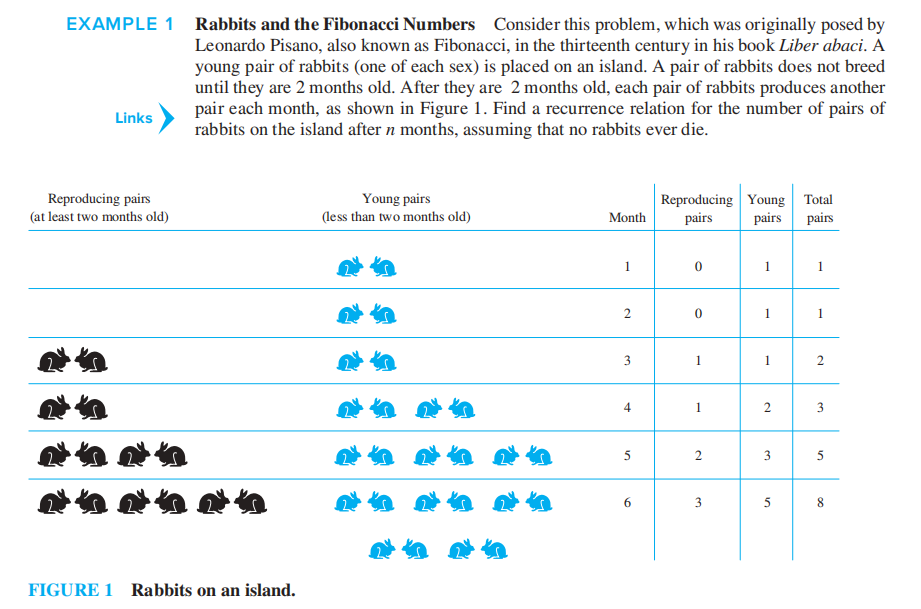
例子

斐波那契数与兔子繁殖问题汉诺塔问题 (the tower of Hanoi puzzle) 关于位串码字枚举添加括号改变乘法顺序

看到 "Total pairs" 那列数的特征，不难发现这是一个斐波那契数，因此递推关系为：

\[ f_n = \begin{cases}f_{n - 1}+f_{n-2} & \text{if } n \ge 3 \\ 1 & \text{if } n = 1 \text{ or } n = 2\end{cases} \]

其中，$f_{n - 1}$ 表示上个月已有的兔子，$f_{n - 2}$ 表示具有生育能力 (2 个月及以上 ) 的兔子繁殖的后代，它们的总和即为这个月的兔子总数

解：完成这一目标分为三步

将上面的 $n - 1$ 个盘子移到第三个销钉上 ($H_{n - 1}$ 步 )
将最大的盘子移到第二个销钉上 (1 步 )
最后将那 $n - 1$ 个盘子移到第二个销钉上 ($H_{n - 1}$ 步 )

因此，我们得到递推关系：$H_n = 2H_{n - 1} + 1$

初始条件：$H_1 = 1$

最后，我们可以得到 $H_n = 2^n - 1$

注：汉诺塔问题有多种变种问题，其中较为知名的是Reve's puzzle：本质上是有四个销钉的汉诺塔问题 ( 还是原来的那套规则 )。虽然没有人能够得到求解具有 $p$ 个销钉的泛化汉诺塔问题的最小移动步数的通法，但是有人已经证明有 4 个销钉的汉诺塔问题的算法。

某个变种 ( 来自课后习题 )

题目答案

解：分为 2 种情况：

以 1 结尾的 n 位位串：只要在长度为 $n-1$ 的位串末尾添加 1 即可，因此有 $a_{n - 1}$ 个位串
以 0 结尾的 n 位位串：易知倒数第二位一定是 1( 否则违反了 " 不存在 2 个连续的 0" 的条件 )，那么问题可以转化为在长度为 $n-2$ 的位串末尾添加“10”，因此有 $a_{n - 2}$ 个位串

综上，我们可以得到递推关系：$a_n = a_{n - 1} + a_{n - 2}, n \ge 3$

易知初始条件为：$a_1 = 2, a_2 = 3$

注：$a_n = f_{n + 2}$（斐波那契数）

解：分 2 种情况讨论：

在 $n - 1$ 位合法( 偶数个 0) 字符串末尾添加除了 0 以外的数字，因此有 $9a_{n - 1}$ 个 $n$ 位合法字符串
在 $n - 1$ 位非法( 奇数个 0) 字符串末尾添加 0( 奇数变偶数，现在就合法了 )，因此有 $10^{n - 1} - a_{n - 1}$ 个 $n$ 位合法字符串

综上，递推关系：$a_n = 9a_{n - 1} + (10^{n - 1} - a_{n - 1}) = 8a_{n -1} + 10^{n - 1}$

分析：

观察到有一个乘法运算符一定在所有括号之外，因为它要执行最后的乘法运算
那么，我们假设最后的乘号在 $x_k$ 和 $x_{k+1}$ 之间，那么就有 $C_kC_{n - k - 1}$ 种添加括号的方法 ($C_k$ 代表运算符前面 $k$ 个数添加括号的方法数，$C_{n - k - 1}$ 代表运算符后面 $n - k - 1$ 个数添加括号的方法数 )
最后，可以得到递推关系

\[ \begin{align}C_n = & C_0C_{n - 1} + C_1C_{n - 2} + \dots + C_{n - 2}C_1 + C_{n - 1}C_0 \notag \\ = & \sum\limits_{k = 0}^{n - 1}C_kC_{n - k - 1} \notag \end{align} \]

其中初始条件为 $C_0 = 1, C_1 = 1$

最后我们可以得到 $C_n = \dfrac{C(2n, n)}{n + 1}$，且 $C_n \sim \frac{4^n}{n^{3/2}\sqrt \pi}$
序列 $\{C_n\}$ 被称为卡特兰数 (Catalan numbers)，除了上述例子外，它可以解决很多的计数问题 ( 就我所知，它可以计算出栈的所有情况数 ( 入栈的元素是递增的 )。具体可戳这 )

Algorithms and Recurrence Relations⚓︎

在很多对算法及其复杂度的研究中，递推关系发挥着重要作用，比如：

分治算法 (divide-and-conquer algorithm)
动态规划 (dynamic programming)：将问题递归拆分成更简单的、可重叠的子问题，然后通过子问题的解来计算整个问题的解，这个过程就需要用到递推关系

分支算法在 8.3 节会详细阐述，这里我们仅讨论动态规划，下面会通过一个典型🌰来解释其中的思想：

例题

之前的例子中，我们用贪心算法求得在同一大厅里安排讲座的最优解，现在稍微改变一下条件：对于每场讲座，新增变量 $w_i$，表示每场讲座到座的学生数。

修改后的问题：有 $n$ 场讲座，讲座 $j$ 在 $t_j$ 时刻开始，在 $e_j$ 时刻结束，会有 $w_j$ 位学生到场。现在我们要安排讲座，使得所有安排上的讲座的到场学生总人数最大。

预先处理：

我们用 $T(j)$ 表示到场的最大人数，它是前 $j$ 个讲座中得到的最优安排。因此 $T(n)$ 表示到场的最大人数，它是从所有 $n$ 个讲座中得到的最优安排
首先，我们按照结束时间对所有讲座按升序排序，然后根据排好的顺序重新给 $n$ 个讲座编号，使得 $e_1 \le e_2 \le \dots \le e_n$
如果两场讲座能放在相同的安排中，也就是说，它们在时间上不重叠，称这两场讲座是可兼容的 (compatible)。我们用 $p(j)$ 表示最大的整数 $i$，$i < j$ 且 $e_i \le s_j$；如果不存在这样的整数，则 $p(j) = 0$

具体问题：

分析：

我们首先得到递推关系，若 $j \le n$，则前 $j$ 场讲座中的最优安排有两种可能：
- 把讲座 $j$ 纳入最优安排中：显然，讲座 $p(j) + 1, \dots, j - 1$ 不会出现在最优安排中，因为它们与讲座 $j$ 不兼容。而且，最优安排一定包含讲座 $1, 2, \dots, p(j)$ 的某几个。因此加上讲座 $j$，我们得到 $T(j) = w_j + T(p(j))$
- 不把讲座 $j$ 纳入最优安排中：此时来自讲座 $1, 2, \dots, j$ 的最优安排等同于来自讲座 $1, 2, \dots, j - 1$ 的最优安排，即 $T(j) = T(j - 1)$
因此，我们得到递推关系：$T(j) = \max(w_j + T(p(j)), T(j - 1))$

下面，我们通过伪代码实现这一算法。注意，我们通过存储每个 $T(j)$ 的值来提高算法效率，因为这样只需要计算一次 $T(j)$ 即可，否则的话算法的最坏复杂度就是指数级的。我们将这一过程被称为记忆 (memorization)

注：上述算法只能算出最多的到场人数，没有得到最优安排中包含哪些讲座。为了确定哪些讲座被包含在最优安排中，我们需要利用这一事实：当且仅当 $w_j + T(p(j)) \ge T(j - 1)$ 时，讲座 $j$ 会在前 $j$ 个讲座的最优安排中。具体算法这里就不写了 ( 这是道练习题 )

Supplements(from Exercises)⚓︎

令 $S(m, n)$ 为从具有 $m$ 个元素的集合映射到具有 $n$ 个元素的集合的满射 (onto) 函数的所有可能情况数，它满足递推关系：$S(m, n) = n^m - \sum\limits_{i = 1}^{n - 1}C(n, k)S(m, k)$，其中 $m \le n$，且 $n > 1$，初始条件为 $S(m, 1) = 1$
约瑟夫问题 (Josephus problem)：有 $n$ 个人，编号为 $1 \sim n$，站成一个圈。从 1 号开始报数，报到 x 的人淘汰，然后被淘汰的人的下一个人重新从 1 开始报数，直到只剩下一人，用 $J(n)$ 表示幸存者的编号 ( wiki )
解决 Reve's puzzle 的算法：Frame-Stewart algorithm
逆向差分 (backward difference)：通过一下方法递归定义：
- 第一差分 (first difference)：$\nabla a_n = a_n - a_{n - 1}$
- 第 $(k+1)$ 差分 ($(k+1)$st difference)：$\nabla ^{k + 1}a_n = \nabla ^k a_n - \nabla ^k a_{n - 1}$ 差分方程：包含序列 $\{a_n\}$( 关于 $a_n, \nabla a_n, \nabla ^2 a_n, \dots$) 及其差分的方程

Solving Linear Recurrence Relations⚓︎

$k$ 阶常系数线性齐次递推关系 (linear homogeneous recurrence relation of degree $k$ with constant coefficient)：用下列形式表示的递推关系 $$ a_n = c_1a_{n - 1} + c_2a_{n - 2} + \dots + c_ka_{n - k} $$ 其中$c_1, c_2, \dots, c_k$为实数，且$c_k \ne 0$

特征：

线性 (linear)：等号右边是序列中前几项与常系数之积的和
齐次 (homogeneous)：每项次数不超过 1
常数 (constant)：序列中的每一项系数都是常数，而非关于 $n$ 的函数
k 阶 (degree)：$a_n$ 是由序列中的前k项表达的

通过强归纳法，满足这种递推关系的序列由递推关系和 $k$ 个首条件 $a_0 = C_0, a_1 = C_1, \dots, a_{k - 1} = C_{k - 1}$ 表示

Solving Linear Homogeneous Recurrence Relations with Constant Coefficients⚓︎

如何求解

关键 1 关键 2

这种递推关系有形如 $a_n = r^n$ 的解，$r$ 为常数。如果这个是递推关系的解，则它的充要条件是 $r^n = c_1r^{n - 1} + c_2r^{n - 2} + \dots + c_kr^{n - k}$
然后两边同除以 $r^{n - k}$($r \ne 0$)，将等号右边的东西全部移到左边，得到 $$ r^k - c_1r^{k - 1} - c_2r^{k - 2} - \dots - c_{k - 1} r - c_k = 0 $$ 因此，当且仅当$r$是上述方程的解时，$a_n = r^n$为递推关系的解。我们称上述方程为特征方程 (characteristic equation)，称这个方程的解为特征根 (characteristic roots)

线性齐次递推关系的两个解的线性组合也是它的解。如果

\[ \begin{align}s_n & = c_1s_{n - 1} + c_2s_{n - 2} + \dots + c_ks_{n - k} \notag \\ t_n & = c_1t_{n - 1} + c_2t_{n - 2} + \dots + c_kt_{n - k}\notag \end{align} \]

那么

\[ \begin{align} b_1s_n + b_2t_n = & b_1(c_1s_{n - 1} + c_2s_{n - 2} + \dots + c_ks_{n - k}) + b_2(c_1t_{n - 1} + c_2t_{n - 2} + \dots + c_kt_{n - k}) \notag \\ = & c_1(b_1s_{n - 1} + b_2t_{n - 1}) + c_2(b_1s_{n - 2} + b_2t_{n - 2}) + \dots + c_k(b_1s_{n - k} + b_2t_{n - k}) \notag \end{align} \]

其中 $b_1, b_2$ 为实数。那么 $b_1s_n + b_2t_n$ 显然也为相同的线性齐次递推关系的解

先从 ~~简单的~~ 二阶情况分析：

定理 1：令 $c_1, c_2$ 为实数。假设 $r^2 - c_1r - c_2 = 0$ 有两个不同的解 $r_1, r_2$，那么当且仅当 $a_n = \alpha_1r_1^n + \alpha_2r_2^n$($n = 0,1,2, \dots$，且 $\alpha_1, \alpha_2$ 为常数 ) 时，序列 $\{a_n\}$ 是递推关系 $a_n = c_1a_{n - 1} + c_2a_{n - 2}$ 的解

证明

如果 $r_1, r_2$ 为特征方程的根，且 $\alpha_1, \alpha_2$ 为常数，那么序列 $\{a_n\}$ 是递推关系 $a_n = c_1a_{n - 1} + c_2a_{n - 2}$ 的解

如果序列 $\{a_n\}$ 是解，那么对于某些常数 $\alpha_1, \alpha_2$，$a_n = \alpha_1r_1^n + \alpha_2r_2^n$

通过上述证明，我们已经知道 $\{a_n\}$ 和 $\{\alpha_1r_1^n + \alpha_2r_2^n\}$ 都是递推关系的解，且当 $n = 0$ 和 $n = 1$ 时满足首条件，因为对于有 2 个首条件的 2 阶线性齐次递推关系有唯一解，因此 $a_n = \alpha_1r_1^n + \alpha_2r_2^n$

注：我们有可能会得到复数根，但这不在我们的讨论范围内

🌰：斐波那契数公式

定理 2 用来处理重根的情况

定理 2：令 $c_1, c_2$ 为实数，且 $c_2 \ne 0$。假设 $r^2 - c_1r - c_2 = 0$ 只有一个根 $r_0$，那么当且仅当 $a_n = \alpha_1r_0^n + \alpha_2nr_0^n$($n = 0,1,2, \dots$，且 $\alpha_1, \alpha_2$ 为常数 ) 时，序列 $\{a_n\}$ 是递推关系 $a_n = c_1a_{n - 1} + c_2a_{n - 2}$ 的解

🌰

讨论更一般的情况：

定理 3：令 $c_1, c_2, \dots, c_k$ 为实数。假设特征方程

\[r^k - c_1r^{k - 1} - c_2r^{k - 2} - \dots - c_{k - 1}r - c_k = 0\]

有 $k$ 个不同的根 $r_1, r_2, \dots, r_k$，那么当且仅当

\[ a_n = \alpha_1r_1^n + \alpha_2r_2^n + \dots + \alpha_kr_k^n \]

其中 $n = 0,1,2, \dots$，且 $\alpha_1, \alpha_2, \dots, \alpha_k$ 为常数，序列 $\{a_n\}$ 是递推关系

\[a_n = c_1a_{n - 1} + c_2a_{n - 2} + \dots + c_ka_{n - k}\]

的解

定理 4：令 $c_1, c_2, \dots, c_k$ 为实数。假设特征方程

\[r^k - c_1r^{k - 1} - c_2r^{k - 2} - \dots - c_{k - 1}r - c_k = 0\]

有 $t$ 个不同的根 $r_1, r_2, \dots, r_t$，重数分别为 $m_1, m_2, \dots, m_t$，满足 $m_i \ge 1$($i = 1, 2, \dots, t$)，且 $m_1 + m_2 + \dots + m_t = k$，那么当且仅当

\[ \begin{align}a_n = & (\alpha_{1, 0} + \alpha_{1, 1}n + \dots + \alpha_{1, m_1 - 1}n^{m_1 - 1})r_1^n \notag \\ & + (\alpha_{2, 0} + \alpha_{2, 1}n + \dots + \alpha_{2, m_2 - 1}n^{m_2 - 1})r_2^n \notag \\ & + \dots + (\alpha_{t, 0} + \alpha_{t, 1}n + \dots + \alpha_{t, m_t - 1}n^{m_t - 1})r_t^n \notag \end{align} \]

其中 $n = 0,1,2, \dots$，且 $\alpha_{i, j}$($1 \le i \le t, 0 \le j \le m_i - 1$) 为常数，序列 $\{a_n\}$ 是递推关系

\[a_n = c_1a_{n - 1} + c_2a_{n - 2} + \dots + c_ka_{n - k}\]

的解

Linear Nonhomogeneous Recurrence Relations with Constant Coefficients⚓︎

常系数线性非齐次递推关系 (linear nonhomogeneous recurrence relation with constant coefficient)：用下列形式表示的递推关系 $$ a_n = c_1a_{n - 1} + c_2a_{n - 2} + \dots + c_ka_{n - k} + F(n) $$ 其中$c_1, c_2, \dots, c_k$为实数，$F(n)$是不等于0，且仅由$n$决定的函数

递推关系 $$ a_n = c_1a_{n - 1} + c_2a_{n - 2} + \dots + c_ka_{n - k} $$ 被称为关联齐次递推关系 (associated homogeneous recurrence relation)

如何求解？

定理 5：如果 $\{a_n^{(p)}\}$ 是常系数线性非齐次递推关系的特殊解 (particular solution)，那么所有的解具有 $\{a_n^{(p)} + a_n^{(h)}\}$ 的形式，其中 $\{a_n^{(h)}\}$ 是关联齐次递推关系的解

证明

虽然没有通法来找到关于任意函数 $F(n)$ 的解，但是对于某些类型的函数，比如多项式或者常数幂，是有办法可以解决的，定理 6 给出了方法：

定理 6：假设 $\{a_n\}$ 满足线性非齐次递推关系 $$ a_n = c_1a_{n - 1} + c_2a_{n - 2} + \dots + c_ka_{n - k} + F(n) $$

其中 $c_1, c_2, \dots, c_k$ 为实数，且

\[F(n) = (b_tn^t + b_{t - 1}n^{t - 1} + \dots + b_1n + b_0)s^n\]

其中 $b_0, b_1, \dots , b_t$ 和 $s$ 为实数。

如果 $s$ 不是关联齐次递推关系的特征方程的根，那么就有以下形式的特殊解：

\[ (p_tn^t + p_{t-1}n^{t-1} + \dots + p_1n + p_0)s^n \]

如果 $s$ 是特征方程的根，且重数为 $m$，那么就有以下形式的特殊解：

\[ n^m(p_tn^t + p_{t-1}n^{t-1} + \dots + p_1n + p_0)s^n \]

例题

例 1 例 2

Supplements(from Exercises)⚓︎

斐波那契数 $f_{n+1} = C(n, 0) + C(n - 1. 1)+ \dots + C(n - k, k)$，其中 $n$ 为正整数，且 $k = \lfloor \dfrac{n}{2} \rfloor$

Divide-and-Conquer Algorithms and Recurrence Relations⚓︎

Generating Functions⚓︎

定义：实数序列 $a_0, a_1, \dots, a_k, \dots$ 的生成函数 (generating functions)是一个无限级数： $$ G(x) = a_0 + a_1x + \dots + a_kx^k + \dots = \sum\limits_{k = 0}^\infty a_kx^k $$

注：这种形式的生成函数有时称作普通生成函数 (ordinary generating function)，用于区分其他形式的生成函数

定义有限实数序列 $a_0, a_1, \dots, a_n$ 的生成函数：令 $a_{n+1} = 0, a_{n+2} = 0$，以此类推，这样将无限序列缩小至有限序列。因此这种无限序列 $\{a_n\}$ 的生成函数 $G(x)$ 就变成一个 $n$阶多项式($a_jx^j = 0, j > n$) $$ G(x) = a_0 + a_1x + \dots + a_nx^n $$ 🌰

Useful Facts About Power Series⚓︎

定理 1：令 $f(x)=\sum\limits_{k=0}^{\infty}a_kx^k,\ g(x)=\sum\limits_{k=0}^{\infty}b_kx^k$，那么

\[ f(x) + g(x) = \sum\limits_{k=0}^{\infty}(a_k+b_k)x^k \quad f(x)g(x) = \sum\limits_{k=0}^\infty (\sum\limits_{j=0}^ka_jb_{k-j})x^k \]

注：定理 1 仅在幂级数在区间内收敛 (converge)时有效 ( 本节中所有级数均认为是收敛的 )。然而生成函数的理论并不局限于这种级数，在那样的情况下级数就不一定收敛了。定理 1 可以作为生成函数的加法和乘法的定义

例题

例 1 例 2

利用幂级数乘法的特征
答案可作为结论使用

( 摘自期中卷 )

定义：令 $u$ 为实数，$k$ 为非负整数。那么扩展二项式系数 (extended binomial coefficient)$\left( \begin{array}{cccc}u \\ k\end{array}\right)$ 可定义为：

\[ \left( \begin{array}{cccc}u \\ k\end{array}\right) = \begin{cases}\dfrac{u(u-1)\dots(u-k+1)}{k!} & \text{if }k > 0 \\ 1 & \text{if } k = 0\end{cases} \]

注：如果二项式系数的首参数是负整数，那么扩展二项式系数可用一般二项式系数表示：$\left( \begin{array}{cccc} -n \\ r\end{array}\right) = (-1)^r\left( \begin{array}{cccc} n + r - 1 \\ r\end{array}\right) = (-1)^rC(n+r-1, r)$

定理 2——扩展二项式定理 (THE EXTENDED BINOMIAL THEOREM)：令 $x$ 为实数且 $|x| < 1$，$u$ 为实数，那么

\[ (1+x)^u = \sum\limits_{k = 0}^\infty \left( \begin{array}{cccc} u \\ k\end{array}\right)x^k \]

注：

定理 2 需要用麦克劳林级数证明

当 $u$ 为正整数，该定理就降级为一般的二项式定理（注意：当 $k > u$ 时，$\left( \begin{array}{cccc} u \\ k\end{array}\right) = 0$)

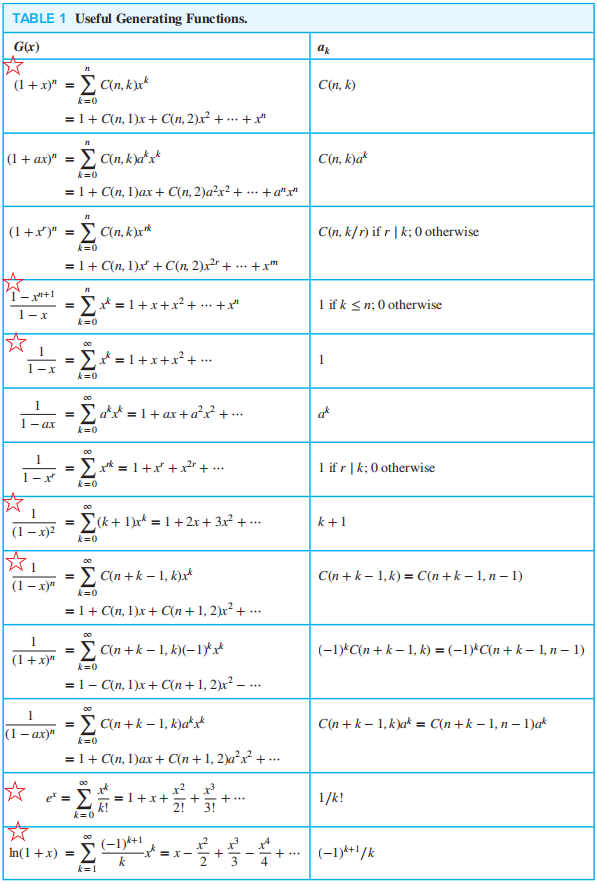
🌟常用的生成函数表 ( vgf 也用得到 )

注：上面十三个生成函数中，重点记忆标⭐的核心公式，其他公式都是在这些核心公式的基础上推出来的

Counting Problems and Generating Functions⚓︎

生成函数可用来解决 $n$ 元素集合中的可重 $r$ 组合问题，比如这种形式： $$ e_1 + e_2 + \dots + e_n = C $$ 其中$C$是常数，$e_i$为非负整数且可能有一些具体限制。

利用生成函数计算 $n$ 元素集合中的可重 $r$ 组合的个数

易知生成函数 $G(x) = (1 + x + x^2 + \dots)^n = \dfrac{1}{(1-x)^n} = (1-x)^{-n}(|x| < 1)$

又因为 $(1-x)^{-n} = (1 + (-x))^{-n} = \sum\limits_{r = 0}^\infty \left( \begin{array}{cccc} -n \\ r\end{array}\right)(-x)^r$( 扩展二项式定理 )

而 $\left( \begin{array}{cccc} -n \\ r\end{array}\right)(-1)^r = (-1)^rC(n+r-1, r) \cdot (-1)^r = C(n+r-1, r)$( 见扩展二项式系数下面的注 )

所以结果为 $C(n + r - 1, r)$，与第 6 章的结论相同

：拓展 ( 答案可作为结论记忆 )

例题

例 1 例 2

注：要理解为什么是否考虑顺序会产生不同的生成函数

Using Generating Functions to Solve Recurrence Relations⚓︎

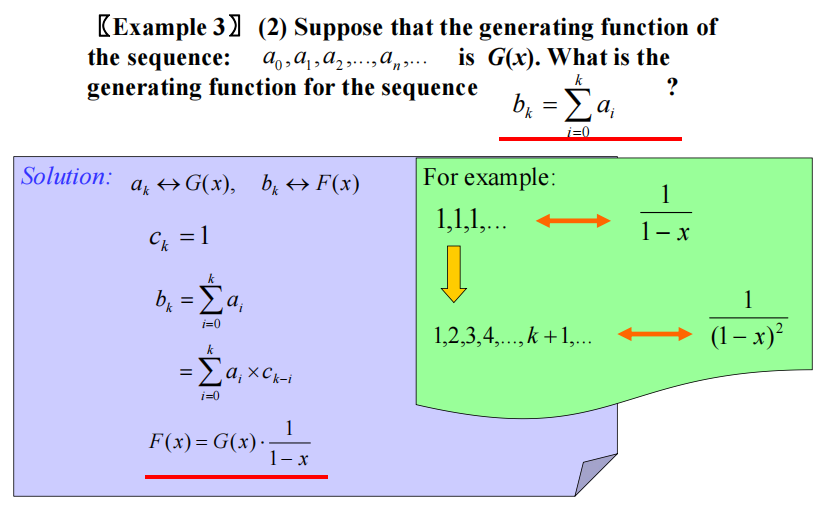
直接看这个🌰，就能理解怎么用生成函数求解递推关系的问题

注意等号两边乘 $x^n$ 后再求和时的起始项问题 (Solution 的第 3 行 )：若递推关系中的最小项为 $a_{n - k}$，则起始项从 $n = k$ 开始，且一定要一致

Proving Identities via Generating Functions⚓︎

例题

例 1 例 2

Supplements(from Exercises)⚓︎

指数生成函数 (exponential generating functions)：$\sum\limits_{n=0}^{\infty}\dfrac{a_n}{n!}x^n$
概率生成函数 (probability generating functions)：$G_X(x) = \sum\limits_{k = 0}^\infty p(X(s) = k)x^k$

Inclusion-Exclusion⚓︎

The Principle of Inclusion-Exclusion⚓︎

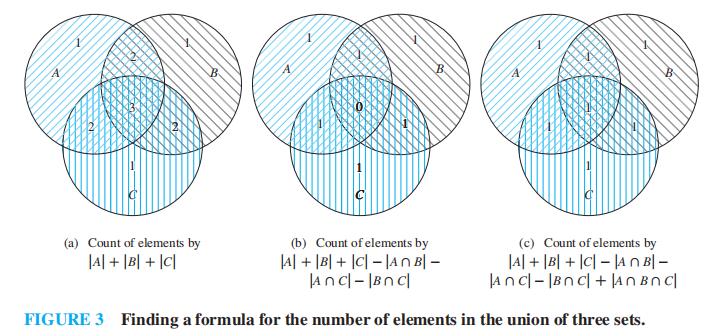
在之前，我们已经了解计算两个集合 $A , B$ 的并集的元素个数公式： $$ |A \cup B| = |A| + |B| - |A \cap B| $$ 这个公式被称为容斥原理 (the principle of inclusion-exclusion)。现在，我们将它扩展至三个集合的公式： $$ |A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C| $$ 推导过程可以用Venn图清楚地展现：

最后，我们将容斥原理运用于 $n$ 个集合，于是有了下面的定理：

定理 1——容斥原理 (THE PRINCIPLE OF INCLUSIVE-EXCLUSIVE)：令 $A_1, A_2, \dots, A_n$ 为有限集合，那么：

\[ \begin{align} |A_1 \cup A_2 \cup \dots \cup A_n| = & \sum\limits_{1 \le i \le n} |A_i| - \sum\limits_{1 \le i < j \le n} |A_i \cap A_j| \notag \\ + & \sum\limits_{1 \le i < j < k \le n} |A_i \cap A_j \cap A_k| - \dots + (-1)^{n+1}|A_1 \cap A_2 \cap \dots \cap A_n| \notag \end{align} \]

证明

我们要证明并集中的每个元素仅被算了一遍。假设 $a$ 是 $A_1, A_2, \dots, A_n$ 中 $r$ 个集合的共有元素 ($1 \le r \le n$)
在 $\sum|A_i|$ 中，这个元素被算了 $C(r, 1)$ 次。在 $\sum|A_i \cap A_j|$ 中，这个元素被算了 $C(r, 2)$ 次。更一般的，在 $m$ 个集合的并集之和中，这个元素被算了 $C(r, m)$ 次
通过等号右侧公式，我们可以计算这个元素总共被算了 $C(r, 1) - C(r, 2) + C(r, 3) - \dots + (-1)^{r+1}C(r, r)$ 次
由 6.4 节引理 2 知，$\sum\limits_{k = 0}^n(-1)^k\left( \begin{array}{cccc}n \\ k\end{array}\right) = 0$ ，所以 $\sum\limits_{k = 1}^n(-1)^{k+1}C(r, k) = 1$ ，这就说明该元素仅被算了一遍，这就证明了上述定理的正确性

注：对于 $n$ 个集合的容斥原理，等号右边有 $2^n-1$ 项

Applications of Inclusion-Exclusion⚓︎

An Alternative Form of Inclusion-Exclusion⚓︎

容斥原理的另一种可替换的形式：求解集合中不满足所有 $n$ 条性质 $P_1, P_2, \dots, P_n$ 的元素个数

分析：令$A_i$表示具有满足性质$P_i$的元素的子集。具有所有$P_{i_1}, P_{i_2}, \dots, P_{i_k}$的性质的元素个数记为$N(P_{i_1}, P_{i_2}, \dots, P_{i_k})$，所以 $$ |A_{i_1} \cap A_{i_2} \cap \dots \cap A_{i_k}| = N(P_{i_1}, P_{i_2}, \dots, P_{i_k}) $$ 那么我们要求的就是$N(P_1' P_2' \dots P_n')$，则 $$ N(P_1' P_2' \dots P_n') = N - |A_1 \cup A_2 \cup \dots \cup A_n| $$ 由容斥原理，我们可以得到：

\[ \begin{align} N(P_1' P_2' \dots P_n') & = N - N(P_1P_2 \dots P_n) \notag \\ & = N - \sum\limits_{1 \le i \le n} N(P_i) + \sum\limits_{1 \le i < j \le n} N(P_iP_j) \notag \\ & - \sum\limits_{1 \le i < j < k \le n} N(P_iP_jP_k) + \dots + (-1)^{n}N(P_1P_2 \dots P_n) \notag \end{align} \]

来看个🌰：（容斥原理 + 可重 r 组合）

The Sieve of Eratosthenes⚓︎

回顾：埃氏筛

用到上面刚学的方法，我们可以求得 100 以内的质数个数为 $$ 4 + N(P_1'P_2'P_3'P_4') $$ 其中'4'代表小于$\sqrt{10}$的4个质数2,3,5,7，$P_1$代表能被2整除的数，$P_2$代表能被3整除的数，$P_3$代表能被5整除的数，$P_4$代表能被7整除的数

后续过程：

The Number of Onto Functions⚓︎

定理 1：令 $m, n$ 为正整数，且 $m \ge n$，那么就有 $$ n^m - C(n, 1)(n - 1)^m + C(n, 2)(n - 2)^m - \dots + (-1)^{n - 1}C(n, n - 1)\cdot 1^m $$ 个从有$m$个元素的集合映射到有$n$个元素的集合的满射函数

证明

令 $A = \{a_1, a_2, \dots, a_m\}, B = \{b_1, b_2, \dots, b_n\}$，$P_i$ 表示 $b_i$ 不在函数的范围内，则我们要求的就是 $N(P_1'P_2' \dots P_n')$($P_1'P_2' \dots P_n'$ 表示 $B$ 中所有元素都在函数范围内，即满射)
容易得到

\[\begin{align} N = n^m, \ \sum\limits_{1 \le i \le n}N(P_i) = C(n, 1)(n - 1)^m \notag \\ \sum\limits_{1 \le i < j \le n}N(P_iP_j) = C(n, 2)(n - 2)^m, \notag \\ \dots, \notag \\ (-1)^nN(P_1P_2\dots P_n) = (-1)^nN(P_1P_2 \dots P_n) = 0 \notag \end{align} \]

于是得到上述定理

从有 $m$ 个元素的集合映射到有 $n$ 个元素的集合的满射函数，对应于将 $m$ 个可区分的物体放入 $n$ 个不可区分的箱子，且保证每个箱子非空的问题 ( 传送门 )。

因此，满射函数的个数 = $n!S(m, n)$，其中 $S(m, n)$ 为第二类斯特林数

Derangements⚓︎

错排问题 (derangement)：使得所有物体均不在它原来的位置上的排列，用 $D_n$ 表示 $n$ 个物体的错排个数

定理 2：集合中 $n$ 个元素的错排个数为 $$ D_n = n![1 - \dfrac{1}{1!} + \dfrac{1}{2!} - \dfrac{1}{3!} + \dots + (-1)^n\dfrac{1}{n!}] $$

证明

令 $P_i$ 表示满足将元素 $i$ 固定在原位的排列，那么 $n$ 个元素的错排个数就是 $$ D_n = N(P_1'P_2' \dots P_n') $$ 使用本节开篇得到的公式，可以得到

\[ \begin{align} D_n= & N - \sum\limits_{i} N(P_i) + \sum\limits_{i < j} N(P_iP_j) \notag \\ - & \sum\limits_{i < j < k} N(P_iP_jP_k) + \dots + (-1)^{n}N(P_1P_2 \dots P_n) \notag \end{align} \]

$N = n!$，对 $n$ 个元素的全排列
$N(P_i) = (n - 1)!$，固定 1 个元素，对剩余 $n - 1$ 个元素进行全排列
以此类推，$N(P_{i_1} P_{i_2} \dots P_{i_m}) = (n - m)!$，固定 $m$ 个元素，对剩余 $n - m$ 个元素进行全排列

又因为从 $n$ 个元素中选择 $m$ 个元素固定共有 $C(n, m)$ 中可能的情况，所以 $$ \sum\limits_{1 \le i_1 < i_2 < \dots i_m \le n}N(P_{i_1} P_{i_2} \dots P_{i_m}) = C(n, m)(n - m)! $$ 将所有情况汇总，得到

\[ \begin{align} D_n = & n! - C(n, 1)(n - 1)! + C(n , 2)(n - 2)! - \dots + (-1)^nC(n, n)(n - n)! \notag \\ = & n! - \dfrac{n!}{1!(n - 1)!}(n - 1)! + \dfrac{n!}{2!(n - 2)!}(n - 2)! - \dots + (-1)^n\dfrac{n!}{n!0!}0! \notag \\ = & n![1 - \dfrac{1}{1!} + \dfrac{1}{2!} - \dfrac{1}{3!} + \dots + (-1)^n\dfrac{1}{n!}] \notag \end{align} \]

错排的概率为 $\dfrac{D_n}{n!} = 1 - \dfrac{1}{1!} + \dfrac{1}{2!} - \dots + (-1)^n \dfrac{1}{n!}$

因为 $e^x = \sum\limits_{j = 0}^\infty \dfrac{x^j}{j!}$，所以可以推出 $e^{-1} = \dfrac{D_n}{n!} \approx 0.368$

Supplements(from Exercises)⚓︎

关于错排数 $D_n$ 的递推关系式：

$D_n = (n - 1)(D_{n - 1} + D_{n - 2}),\ n \ge 2$
$D_n = nD_{n - 1} + (-1)^n,\ n \ge 1$

评论区

如果大家有什么问题或想法，欢迎在下方留言~